具有相反意义的量(湖南省益阳市)

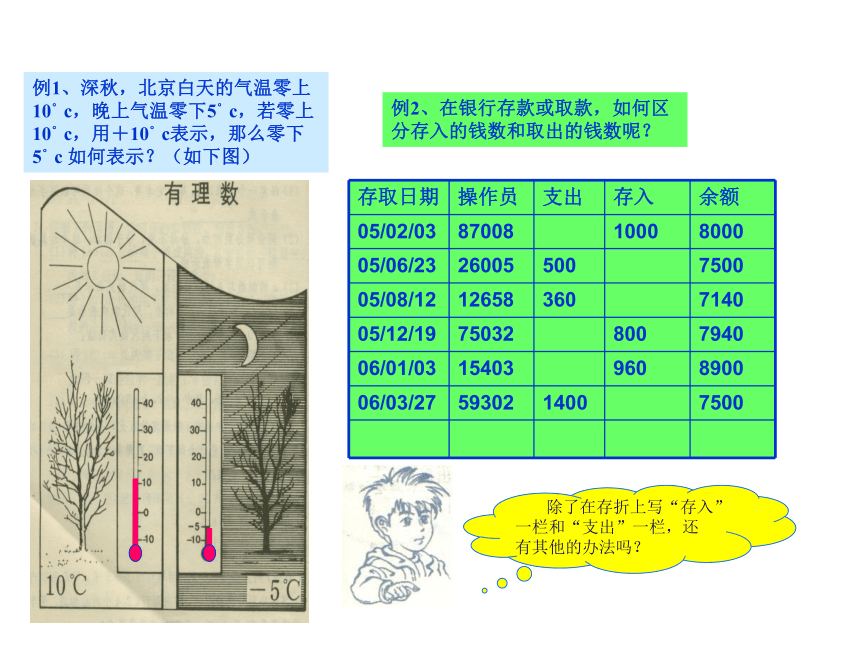
课件17张PPT。1.1具有相反意义的量古代猎人打了一只老鹰，用数如何表示一只老鹰——有了整数 二人分一只西瓜，用数如何表示半只西瓜——有了分数货币购物，用数如何表示2元3角4分——有了小数。仔细观察周围的生活例1、深秋，北京白天的气温零上10°c，晚上气温零下5°c，若零上10°c，用＋10°c表示，那么零下5°c 如何表示？（如下图）例2、在银行存款或取款，如何区分存入的钱数和取出的钱数呢？ 除了在存折上写“存入”一栏和“支出”一栏，还有其他的办法吗？
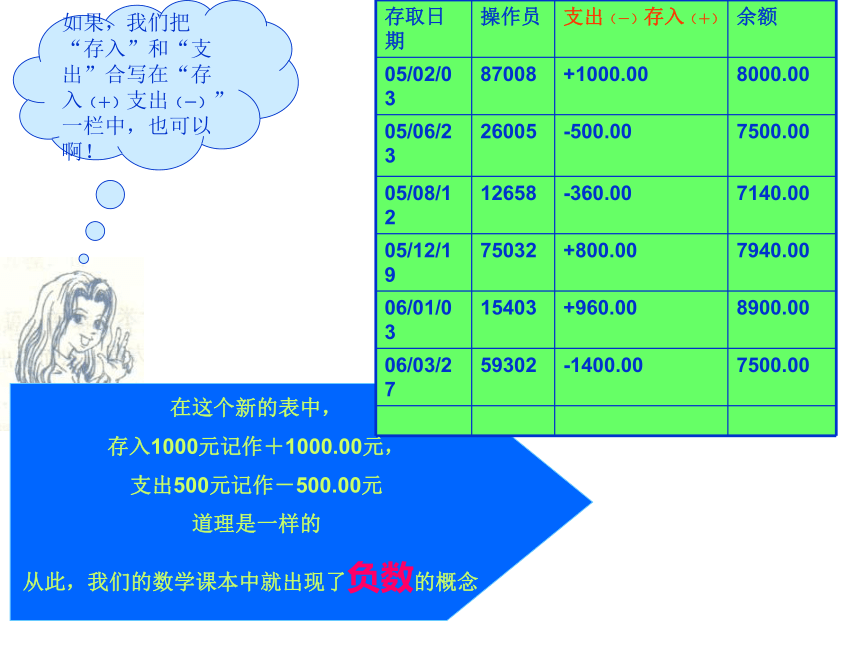
如果，我们把“存入”和“支出”合写在“存入（＋）支出（－）”一栏中，也可以啊！
在这个新的表中，
存入1000元记作＋1000.00元，
支出500元记作－500.00元
道理是一样的
从此，我们的数学课本中就出现了负数的概念抽象是一种思想生活中有很多相对的概念
例如：温度的零上和零下
储蓄的存入和支出
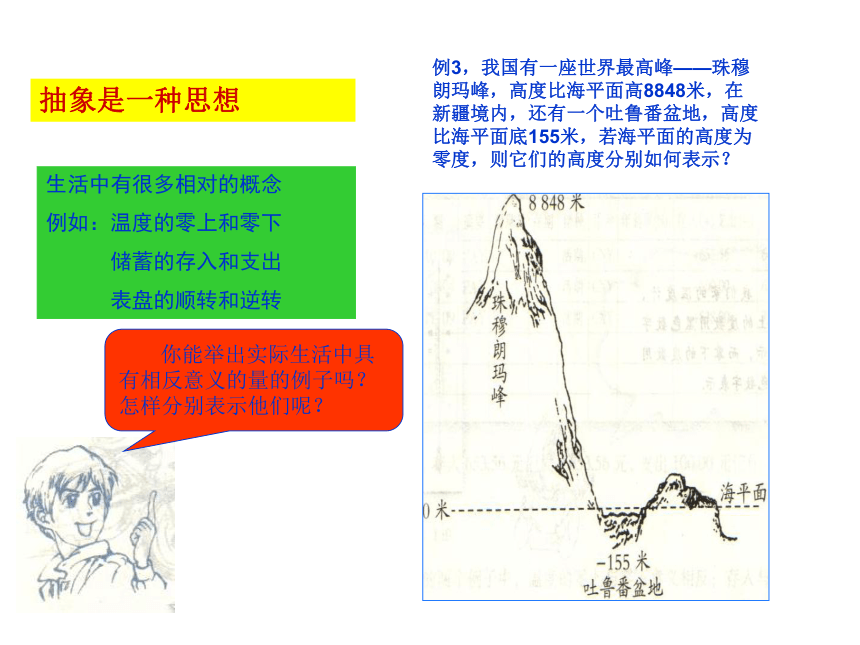
表盘的顺转和逆转 你能举出实际生活中具有相反意义的量的例子吗？怎样分别表示他们呢？例3，我国有一座世界最高峰——珠穆朗玛峰，高度比海平面高8848米，在新疆境内，还有一个吐鲁番盆地，高度比海平面底155米，若海平面的高度为零度，则它们的高度分别如何表示？ 在上面的三个例子中，为了便于区分这些意义相反的量，数学上就规定：
在具有相反意义的一对量中，把其中的一种量用正数（positive number）表示；而另一种量用负数（negative number）表示，它是在正数前面加上“－”（读作负）号。
有的时候在正数前面“＋”号，以强调它是正数。例如，正数5写作＋ 5，但通常把“+”省略不写
0既不是正数，也不是负数。从抽象中总结让我们从以下的几个例子中更好的理解负数的概念加10分扣10分得0分全国主要城市天气预报议一议财富全球强中的主要零售企业单位：百万美元2、我们可以把学过的数归归类：
（1） 正整数（即不为0的自然数）、零和负整数统称为整 数（interger）
(2)正分数和负分数统称为分数（fraction）
(3)整数和分数统称为有理数（rationail number）
所有整数合在一起组成整数集
所有有理数合在一起组成有理数集例1 (1) 在知识竞赛中,如果用+10分表示加10分,那么扣20分怎样表示?解:(1) 扣20分记作-20分 (2) 某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?(2) 沿顺时针方向转12圈记作-12圈(3) 在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02克记作+0.02克,那么-0.03克表示什么?(3) -0.03克表示乒乓球的质量低于标准质量0.03克.(3) -0.03克表示乒乓球的质量低于标准质量0.03克.3、有理数的分类(复习)…… 负分数整数分数有理数……正整数……零……负整数…… 正分数判断题：
1、如果－50元表示支出50元，那么＋200元
表示收入200元。（ ）
2、如果＋10表示提前10分钟到校，那么－5
表示迟到5分钟到校。（ ）20, -8, 0, -1课堂练习：
（１）如果零上5°C记作+5°C，那么零下3°C记作什么?
（２）东、西为两个相反方向，如果-４米表示一个
　　　物体向西运动４米，那么+２米表示什么？物体
　　　原地不动记为什么？　　　　　　　　　　　　　
（３）某仓库运进面粉７·５吨，那么运出３.８吨应记作什么？ （-3°C）（ +２表示物体向东运动2米，不动记为0米）( - 3. 8 吨 ）√√小结：本节课通过实例引进了负数、有理数的概念，学习了负数的表示方法，并会对有理数进行正确的归类.布置作业：