寒假查漏补缺检测卷(一)2023-2024学年数学九年级上册苏科版(含答案)
文档属性
| 名称 | 寒假查漏补缺检测卷(一)2023-2024学年数学九年级上册苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 11:27:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
寒假查漏补缺检测卷(一)2023-2024学年数学九年级上册苏科版
一、选择题
1.为备战中考,同学们积极投入复习,卓玛同学的试卷袋里装有语文试卷2张,藏文试卷3张,英语试卷1张,从中任意抽出一张试卷,恰好是语文试卷的概率是( )
A. B. C. D.
2.现有一列数:6,3,3,4,5,4,3,若去掉一个数后,这列数的中位数仍不变,则的值可能为( )
A.3 B.4 C.5 D.6
3.甲乙两班的学生在同一次数学测试,两班的平均分都是95分,方差分别为,,那么成绩比较整齐的班级是( )
A.甲班 B.乙班
C.两班一样整齐 D.无法确定
4.某机械制造厂制造某种产品,原来每件产品的成本是100元,由于提高生产技术,所以连续两次降低成本,两次降低后的成本是81元,则平均每次降低成本的百分率是( )
A. B. C. D.
5.关于x的二次方程的一个根是0,则a的值为( ).
A.1 B.-1 C.1或-1 D.
6.关于 的方程 有实数根,则 满足( )
A. B. 且
C. 且 D.
7.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心。若∠C=50°,则∠B的大小等于( )
A.20° B.25° C.40° D.50°
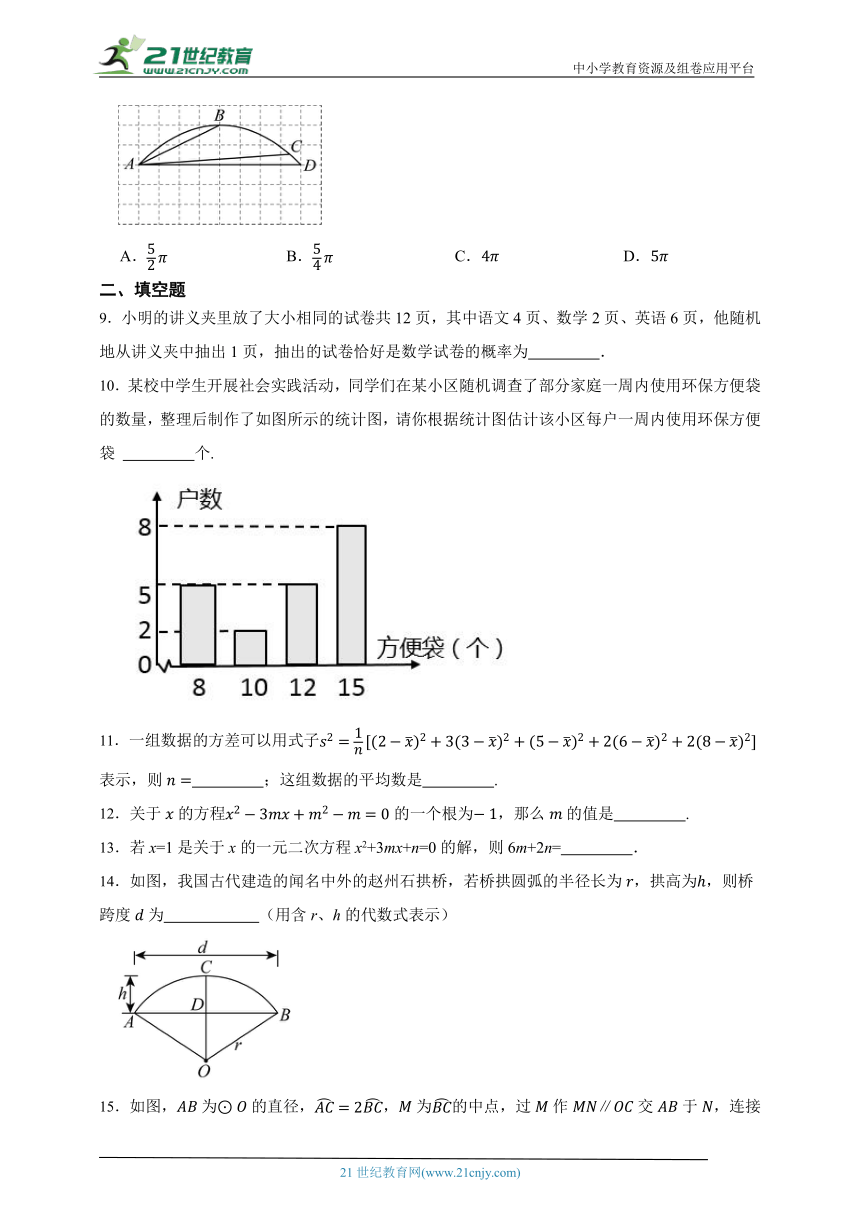
8.如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在弧上,,则的长为( )
A. B. C. D.
二、填空题
9.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页、数学2页、英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为 .
10.某校中学生开展社会实践活动,同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量,整理后制作了如图所示的统计图,请你根据统计图估计该小区每户一周内使用环保方便袋 个.
11.一组数据的方差可以用式子表示,则 ;这组数据的平均数是 .
12.关于的方程的一个根为,那么的值是 .
13.若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n= .
14.如图,我国古代建造的闻名中外的赵州石拱桥,若桥拱圆弧的半径长为,拱高为,则桥跨度为 (用含r、h的代数式表示)
15.如图,为的直径,,为的中点,过作∥交于,连接,则的度数为 .
16.在平面直角坐标系中,已知的半径为2,圆心P在抛物线上运动,当与x轴相切,且圆心P在第二象限内时,圆心P的坐标为 .
三、解答题
17.为了让教师深入理解2022年版课程标准,某校开展了“学习新课标,践行新理念”活动,并组织了2022年版课程标准知识竞赛.甲、乙、丙、丁四名教师在这次校级竞赛活动中成绩优异,该校决定从这四名教师中随机选取两名教师参加市级2022年版课程标准知识竞赛.
(1)“甲、戊两名教师被选到”是 (填“随机”、“必然”或“不可能”)事件.
(2)请用列表或画树状图的方法,求恰好选到甲、乙两名教师的概率.
18.2023年7月5日,星际荣耀“双曲线二号”验证火箭动力系统试车取得圆满成功.为了庆祝这个时刻,某县举办了科技知识活动,根据综合成绩选择一位同学参加市活动.已知嘉嘉与琪琪进入前两名,她们的各项成绩(单项满分100分)如下表所示:
选手 征文 演讲 歌唱
嘉嘉 75分 90分 87分
琪琪 84分 83分 88分
(1)如果把各项成绩的平均分作为综合成绩,应推选谁?
(2)如果把征文、演讲、歌唱三项成绩按的比例作为综合成绩,应推选谁?
19.一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
20.某农场要建一个饲养场(矩形),两面靠墙(位置的墙最大可用长度为25m,位置的墙最大可用长度为21m),另外两边用木栏围成,中间用木栏隔成两个小矩形并在如图所示的两处各留1m宽的门(不用木栏),建成后木栏总长50m.
(1)若饲养场(矩形)的面积为,求边的长;
(2)小芳说:“饲养场的面积最多能达到.”若能达到,求出边的长;若不能达到,请说明理由.
21.如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)请作图找出圆心P的位置,并写出它的坐标.
(2)求的长度.
22.如图,△ABD内接于半圆O,AB是直径,点C是弧BD的中点,连结OC,AC,分别交BD于点F、E.
(1)求证:;
(2)若,求的长.
23.如图,AB为半圆O的直径,C是半圆O上一点,D是的中点,过点D作直线,直线l,垂足为F,BC的延长线交直线l于点E.
(1)求证:直线l是的切线.
(2)若的半径为1,求的值.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】
10.【答案】12
11.【答案】9;
12.【答案】
13.【答案】﹣2
14.【答案】
15.【答案】45°
16.【答案】
17.【答案】(1)不可能
(2)
18.【答案】(1)解:分,分.
,
应推选琪琪
(2)解:嘉嘉的综合成绩为分,
琪琪的综合成绩为分.
,
应推选嘉嘉.
19.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
20.【答案】(1)解:设边的长为m,则的长为m,由题意,得:
,
解得:,
当时,,不符合题意,舍去;
当时,,符合题意,
∴边的长为20m;
(2)解:不能,理由如下:
由题意,得:,整理得:,
∴,
∴,
当时,,不符合题意;
∴饲养场的面积不能达到.
21.【答案】(1)解:如图,点P就是圆弧所在圆的圆心,点P的坐标为:(-2,1);
(2)解:如图,
∵AC2=22+42=20,AP2=PC2=12+32=10,
∴AC2=AP2+PC2,
∴△ACP是直角三角形,且∠APC=90°,
∴ =.
22.【答案】(1)解:点为弧的中点,
,
是半圆的直径,
,
;
(2)解:连结BC,
是半圆的直径,
,
设,则,
即,
解得,
∴OF=1.4,
∵点O是AB的中点,点F是BD的中点,
∴OF是的中位线,
23.【答案】(1)解:证明:如图,连接OD.
∵D是的中点,∴.
又∵直线,∴直线.
∴直线l是的切线.
(2)(解法不唯一,也可通过推理得到)
如图,过点D作,垂足为M.
∵,∴.
又∵,∴.
∵,∴,
∴,∴.
同理可得,∴,
∴,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
寒假查漏补缺检测卷(一)2023-2024学年数学九年级上册苏科版
一、选择题
1.为备战中考,同学们积极投入复习,卓玛同学的试卷袋里装有语文试卷2张,藏文试卷3张,英语试卷1张,从中任意抽出一张试卷,恰好是语文试卷的概率是( )
A. B. C. D.
2.现有一列数:6,3,3,4,5,4,3,若去掉一个数后,这列数的中位数仍不变,则的值可能为( )
A.3 B.4 C.5 D.6
3.甲乙两班的学生在同一次数学测试,两班的平均分都是95分,方差分别为,,那么成绩比较整齐的班级是( )
A.甲班 B.乙班
C.两班一样整齐 D.无法确定
4.某机械制造厂制造某种产品,原来每件产品的成本是100元,由于提高生产技术,所以连续两次降低成本,两次降低后的成本是81元,则平均每次降低成本的百分率是( )
A. B. C. D.
5.关于x的二次方程的一个根是0,则a的值为( ).
A.1 B.-1 C.1或-1 D.
6.关于 的方程 有实数根,则 满足( )
A. B. 且
C. 且 D.
7.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心。若∠C=50°,则∠B的大小等于( )
A.20° B.25° C.40° D.50°
8.如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在弧上,,则的长为( )
A. B. C. D.
二、填空题
9.小明的讲义夹里放了大小相同的试卷共12页,其中语文4页、数学2页、英语6页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为 .
10.某校中学生开展社会实践活动,同学们在某小区随机调查了部分家庭一周内使用环保方便袋的数量,整理后制作了如图所示的统计图,请你根据统计图估计该小区每户一周内使用环保方便袋 个.
11.一组数据的方差可以用式子表示,则 ;这组数据的平均数是 .
12.关于的方程的一个根为,那么的值是 .
13.若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n= .
14.如图,我国古代建造的闻名中外的赵州石拱桥,若桥拱圆弧的半径长为,拱高为,则桥跨度为 (用含r、h的代数式表示)
15.如图,为的直径,,为的中点,过作∥交于,连接,则的度数为 .
16.在平面直角坐标系中,已知的半径为2,圆心P在抛物线上运动,当与x轴相切,且圆心P在第二象限内时,圆心P的坐标为 .
三、解答题
17.为了让教师深入理解2022年版课程标准,某校开展了“学习新课标,践行新理念”活动,并组织了2022年版课程标准知识竞赛.甲、乙、丙、丁四名教师在这次校级竞赛活动中成绩优异,该校决定从这四名教师中随机选取两名教师参加市级2022年版课程标准知识竞赛.
(1)“甲、戊两名教师被选到”是 (填“随机”、“必然”或“不可能”)事件.
(2)请用列表或画树状图的方法,求恰好选到甲、乙两名教师的概率.
18.2023年7月5日,星际荣耀“双曲线二号”验证火箭动力系统试车取得圆满成功.为了庆祝这个时刻,某县举办了科技知识活动,根据综合成绩选择一位同学参加市活动.已知嘉嘉与琪琪进入前两名,她们的各项成绩(单项满分100分)如下表所示:
选手 征文 演讲 歌唱
嘉嘉 75分 90分 87分
琪琪 84分 83分 88分
(1)如果把各项成绩的平均分作为综合成绩,应推选谁?
(2)如果把征文、演讲、歌唱三项成绩按的比例作为综合成绩,应推选谁?
19.一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
20.某农场要建一个饲养场(矩形),两面靠墙(位置的墙最大可用长度为25m,位置的墙最大可用长度为21m),另外两边用木栏围成,中间用木栏隔成两个小矩形并在如图所示的两处各留1m宽的门(不用木栏),建成后木栏总长50m.
(1)若饲养场(矩形)的面积为,求边的长;
(2)小芳说:“饲养场的面积最多能达到.”若能达到,求出边的长;若不能达到,请说明理由.
21.如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)请作图找出圆心P的位置,并写出它的坐标.
(2)求的长度.
22.如图,△ABD内接于半圆O,AB是直径,点C是弧BD的中点,连结OC,AC,分别交BD于点F、E.
(1)求证:;
(2)若,求的长.
23.如图,AB为半圆O的直径,C是半圆O上一点,D是的中点,过点D作直线,直线l,垂足为F,BC的延长线交直线l于点E.
(1)求证:直线l是的切线.
(2)若的半径为1,求的值.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】
10.【答案】12
11.【答案】9;
12.【答案】
13.【答案】﹣2
14.【答案】
15.【答案】45°
16.【答案】
17.【答案】(1)不可能
(2)
18.【答案】(1)解:分,分.
,
应推选琪琪
(2)解:嘉嘉的综合成绩为分,
琪琪的综合成绩为分.
,
应推选嘉嘉.
19.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
20.【答案】(1)解:设边的长为m,则的长为m,由题意,得:
,
解得:,
当时,,不符合题意,舍去;
当时,,符合题意,
∴边的长为20m;
(2)解:不能,理由如下:
由题意,得:,整理得:,
∴,
∴,
当时,,不符合题意;
∴饲养场的面积不能达到.
21.【答案】(1)解:如图,点P就是圆弧所在圆的圆心,点P的坐标为:(-2,1);
(2)解:如图,
∵AC2=22+42=20,AP2=PC2=12+32=10,
∴AC2=AP2+PC2,
∴△ACP是直角三角形,且∠APC=90°,
∴ =.
22.【答案】(1)解:点为弧的中点,
,
是半圆的直径,
,
;
(2)解:连结BC,
是半圆的直径,
,
设,则,
即,
解得,
∴OF=1.4,
∵点O是AB的中点,点F是BD的中点,
∴OF是的中位线,
23.【答案】(1)解:证明:如图,连接OD.
∵D是的中点,∴.
又∵直线,∴直线.
∴直线l是的切线.
(2)(解法不唯一,也可通过推理得到)
如图,过点D作,垂足为M.
∵,∴.
又∵,∴.
∵,∴,
∴,∴.
同理可得,∴,
∴,即.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
