寒假查漏补缺检测卷(二)2023-2024学年数学九年级上册苏科版(含答案)
文档属性
| 名称 | 寒假查漏补缺检测卷(二)2023-2024学年数学九年级上册苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 592.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 12:10:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
寒假查漏补缺检测卷(二)2023-2024学年数学九年级上册苏科版
一、选择题
1.下列事件中,是必然事件的是( )
A.掷一枚硬币,正面朝上
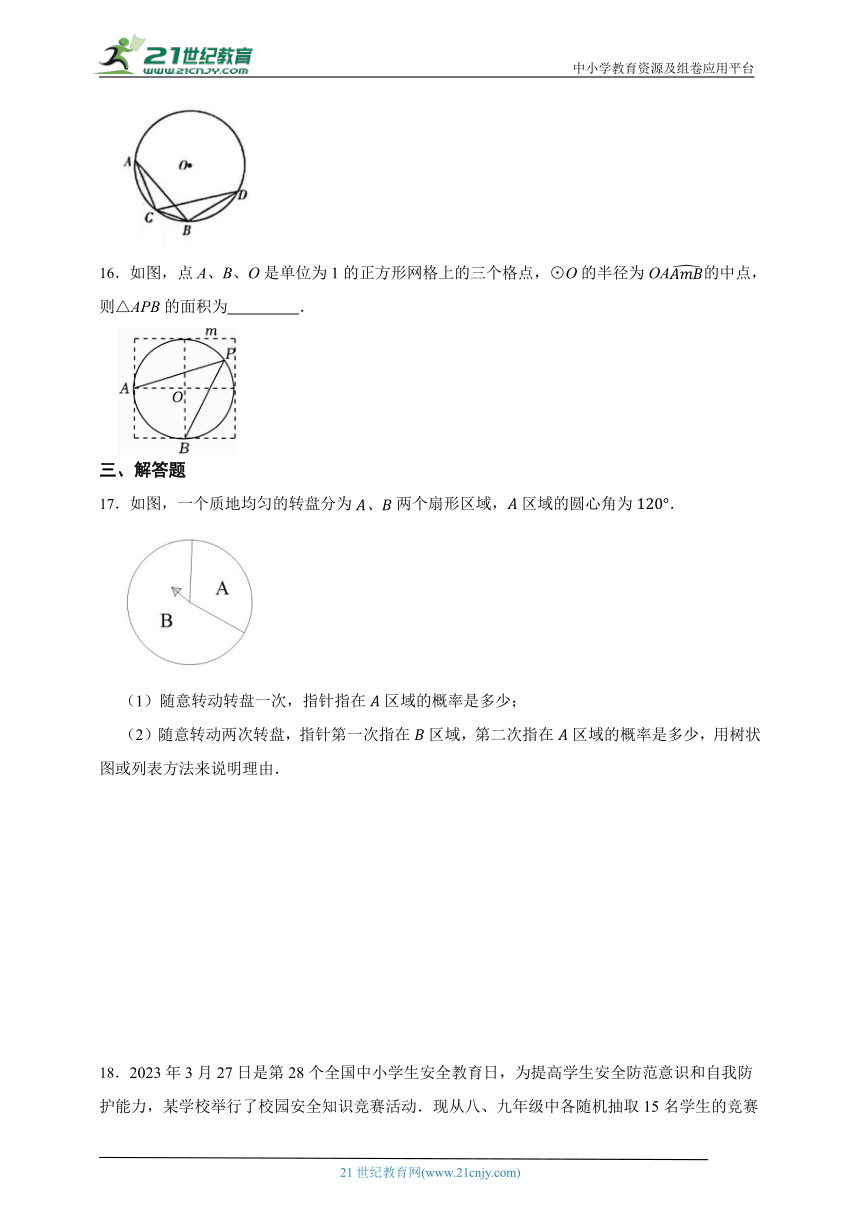
B.购买一张彩票,一定中奖
C.任意画一个三角形,它的内角和等于
D.存在一个实数,它的平方是负数
2.一天晚上,小伟帮助妈妈清洗四个绿、白、蓝、红颜色不同的有盖茶杯,突然停电了,小伟只好随机将其中一个杯盖和一个茶杯搭配在一起.则这个茶杯颜色搭配恰好正确的概率为( )
A. B. C. D.
3.下列说法中,正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.甲、乙两组数据的方差分别是,,则乙组数据比甲组数据稳定
C.“任意画一个三角形,其内角和是”是必然事件
D.从2000名学生中随机抽取100名学生进行调查,样本容量为2000名学生
4.一元二次方程x2-8x-1=0配方后可变形为( )
A.(x+4)2=17 B.(x+4)2=15
C.(x-4)2=17 D.(x-4)2=15
5.一元二次方程的解是( )
A. B.
C., D.无实数解
6.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
7.如图,四边形是的内接四边形,连接,若,则的度数是( )
A. B. C. D.
8.如图,的半径为2,圆心M的坐标为,点P是上的任意一点,,且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为( )
A.9 B.10 C.12 D.14
二、填空题
9.小明与父母从广州乘火车回梅州参观叶帅纪念馆,他们买到的火车票是同一排相邻的三个座位,那么小明恰好坐在父母中间的概率是 .
10.年月日青海省玉树县发生级大地震后,湘江中学九年级班的名同学踊跃捐款、有人每人捐元、人每人捐元、人每人捐元、人每人捐元.在这次每人捐款的数值中,中位数是 .
11.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:kg/亩,,kg/亩,,则品种 更适合在该村推广.(填“甲”或“乙”)
12.若关于x的方程 是一元二次方程,则m的值是 .
13.若关于x的方程有两个相等的实数根,则的值为 .
14.已知圆锥的母线长为,底面半径为,则它的侧面展开扇形的面积为 .
15.如图,在中,,,则 度.
16.如图,点A、B、O是单位为1的正方形网格上的三个格点,⊙O的半径为OA的中点,则△APB的面积为 .
三、解答题
17.如图,一个质地均匀的转盘分为两个扇形区域,区域的圆心角为.
(1)随意转动转盘一次,指针指在区域的概率是多少;
(2)随意转动两次转盘,指针第一次指在区域,第二次指在区域的概率是多少,用树状图或列表方法来说明理由.
18.2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析成绩得分用x表示,80分及以上为优秀,共分成四组,A:60≤x<70,B:70≤x<80;C:80≤x<90;D:90≤x≤100,并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,
87.八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98 60%
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)根据上述数据,你认为该校八、九年级中,哪个年级校园安全知识掌握更好,请说明理由(一条理由即可);
(3)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
19.关于x的方程x2﹣(m+2)x+(2m﹣1)=0
(1)若此方程的一个根为1,求m的值;
(2)求证:方程恒有两个不相等的实数根.
20.太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.
(1)求每天的销售量y(件)关于x(元)的函数关系式.
(2)在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.
21.如图,正八边形内接于,M是弧DE上的一点,连接AM,BM,求的度数.
22.已知是的直径,点D是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为M,的半径为10,求的长.
23.图1是某型号汤碗,截面如图2所示,碗体部分为半圆O,直径,倒汤时,,如图3所示.
(1)的度数为 ;
(2)在图3中,通过计算比较直径与的长度哪个更长;
(3)请在图3中画出线段,用其长度表示汤(阴影部分)的最大深度(不说理由),并求汤的最大深度.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】
10.【答案】50
11.【答案】乙
12.【答案】1
13.【答案】9
14.【答案】
15.【答案】28
16.【答案】
17.【答案】(1)解:A区域的圆心角为120°,占整个圆的比例为,
所以指针指在A区域的概率是P=;
(2)解:A区域的圆心角为120°,那么B区域的圆心角为240°.
将B区域分成圆心角为120°的两个区域B1,B2
随意转动两次转盘,可画树状图为
指针第一次指在B区域,第二次指在A区域的概率是P=
18.【答案】(1)84;100;80%
(2)解:九年级校园安全知识掌握更好,理由如下:
∵九年级学生竞赛成绩的中位数、众数和优秀率均高于八年级,所以九年级校园安全知识掌握更好;
(3)解:(人),
答:估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数200人.
19.【答案】(1)解:根据题意,得
12﹣1×(m+2)+(2m﹣1)=0,
解得m=2
(2)解:∵Δ=(m+2)2﹣4(2m﹣1)=(m﹣2)2+4,
∴在实数范围内,m无论取何值,(m﹣2)2+4>0,即Δ>0,
∴关于x的方程x2﹣(m+2)x+(2m﹣1)=0恒有两个不相等的实数根;
20.【答案】(1)解:由题意知,当销售单价下降1元时,每天销售量增加4件,
∴;
(2)解:假设衣服每件降价x元,则销售量为件,
∴,
解得:或15
∵售单价不低于150元,
∴每件衣服应降价15元,即销售单价为185元时,该品牌衣服的销售单价定185元时,商场每天利13600元;
21.【答案】解:如图,连接OA,OB.
∵正八边形是的内接正八边形,
∴,
∴.
22.【答案】(1)证明:连接,如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵是的半径,
∴直线是的切线.
(2)解:∵是的直径,且于点M,
∴,,
∵,
∴
∴,
∴,
∴.
23.【答案】(1)
(2)解:∵,
∴,
∵,
∴的长度更长;
(3)解:如图,过圆心作于点,交圆于点,则为汤的最大深度,且,
∵,,
∴.
∵,,
∴,
∴,即汤的最大深度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
寒假查漏补缺检测卷(二)2023-2024学年数学九年级上册苏科版
一、选择题
1.下列事件中,是必然事件的是( )
A.掷一枚硬币,正面朝上
B.购买一张彩票,一定中奖
C.任意画一个三角形,它的内角和等于
D.存在一个实数,它的平方是负数
2.一天晚上,小伟帮助妈妈清洗四个绿、白、蓝、红颜色不同的有盖茶杯,突然停电了,小伟只好随机将其中一个杯盖和一个茶杯搭配在一起.则这个茶杯颜色搭配恰好正确的概率为( )
A. B. C. D.
3.下列说法中,正确的是( )
A.检测“神舟十六号”载人飞船零件的质量,应采用抽样调查
B.甲、乙两组数据的方差分别是,,则乙组数据比甲组数据稳定
C.“任意画一个三角形,其内角和是”是必然事件
D.从2000名学生中随机抽取100名学生进行调查,样本容量为2000名学生
4.一元二次方程x2-8x-1=0配方后可变形为( )
A.(x+4)2=17 B.(x+4)2=15
C.(x-4)2=17 D.(x-4)2=15
5.一元二次方程的解是( )
A. B.
C., D.无实数解
6.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
7.如图,四边形是的内接四边形,连接,若,则的度数是( )
A. B. C. D.
8.如图,的半径为2,圆心M的坐标为,点P是上的任意一点,,且与x轴分别交于A、B两点,若点A、点B关于原点O对称,则的最大值为( )
A.9 B.10 C.12 D.14
二、填空题
9.小明与父母从广州乘火车回梅州参观叶帅纪念馆,他们买到的火车票是同一排相邻的三个座位,那么小明恰好坐在父母中间的概率是 .
10.年月日青海省玉树县发生级大地震后,湘江中学九年级班的名同学踊跃捐款、有人每人捐元、人每人捐元、人每人捐元、人每人捐元.在这次每人捐款的数值中,中位数是 .
11.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:kg/亩,,kg/亩,,则品种 更适合在该村推广.(填“甲”或“乙”)
12.若关于x的方程 是一元二次方程,则m的值是 .
13.若关于x的方程有两个相等的实数根,则的值为 .
14.已知圆锥的母线长为,底面半径为,则它的侧面展开扇形的面积为 .
15.如图,在中,,,则 度.
16.如图,点A、B、O是单位为1的正方形网格上的三个格点,⊙O的半径为OA的中点,则△APB的面积为 .
三、解答题
17.如图,一个质地均匀的转盘分为两个扇形区域,区域的圆心角为.
(1)随意转动转盘一次,指针指在区域的概率是多少;
(2)随意转动两次转盘,指针第一次指在区域,第二次指在区域的概率是多少,用树状图或列表方法来说明理由.
18.2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析成绩得分用x表示,80分及以上为优秀,共分成四组,A:60≤x<70,B:70≤x<80;C:80≤x<90;D:90≤x≤100,并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,
87.八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98 60%
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)根据上述数据,你认为该校八、九年级中,哪个年级校园安全知识掌握更好,请说明理由(一条理由即可);
(3)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
19.关于x的方程x2﹣(m+2)x+(2m﹣1)=0
(1)若此方程的一个根为1,求m的值;
(2)求证:方程恒有两个不相等的实数根.
20.太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.
(1)求每天的销售量y(件)关于x(元)的函数关系式.
(2)在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.
21.如图,正八边形内接于,M是弧DE上的一点,连接AM,BM,求的度数.
22.已知是的直径,点D是延长线上一点,,是的弦,.
(1)求证:直线是的切线;
(2)若,垂足为M,的半径为10,求的长.
23.图1是某型号汤碗,截面如图2所示,碗体部分为半圆O,直径,倒汤时,,如图3所示.
(1)的度数为 ;
(2)在图3中,通过计算比较直径与的长度哪个更长;
(3)请在图3中画出线段,用其长度表示汤(阴影部分)的最大深度(不说理由),并求汤的最大深度.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】
10.【答案】50
11.【答案】乙
12.【答案】1
13.【答案】9
14.【答案】
15.【答案】28
16.【答案】
17.【答案】(1)解:A区域的圆心角为120°,占整个圆的比例为,
所以指针指在A区域的概率是P=;
(2)解:A区域的圆心角为120°,那么B区域的圆心角为240°.
将B区域分成圆心角为120°的两个区域B1,B2
随意转动两次转盘,可画树状图为
指针第一次指在B区域,第二次指在A区域的概率是P=
18.【答案】(1)84;100;80%
(2)解:九年级校园安全知识掌握更好,理由如下:
∵九年级学生竞赛成绩的中位数、众数和优秀率均高于八年级,所以九年级校园安全知识掌握更好;
(3)解:(人),
答:估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数200人.
19.【答案】(1)解:根据题意,得
12﹣1×(m+2)+(2m﹣1)=0,
解得m=2
(2)解:∵Δ=(m+2)2﹣4(2m﹣1)=(m﹣2)2+4,
∴在实数范围内,m无论取何值,(m﹣2)2+4>0,即Δ>0,
∴关于x的方程x2﹣(m+2)x+(2m﹣1)=0恒有两个不相等的实数根;
20.【答案】(1)解:由题意知,当销售单价下降1元时,每天销售量增加4件,
∴;
(2)解:假设衣服每件降价x元,则销售量为件,
∴,
解得:或15
∵售单价不低于150元,
∴每件衣服应降价15元,即销售单价为185元时,该品牌衣服的销售单价定185元时,商场每天利13600元;
21.【答案】解:如图,连接OA,OB.
∵正八边形是的内接正八边形,
∴,
∴.
22.【答案】(1)证明:连接,如图,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵是的半径,
∴直线是的切线.
(2)解:∵是的直径,且于点M,
∴,,
∵,
∴
∴,
∴,
∴.
23.【答案】(1)
(2)解:∵,
∴,
∵,
∴的长度更长;
(3)解:如图,过圆心作于点,交圆于点,则为汤的最大深度,且,
∵,,
∴.
∵,,
∴,
∴,即汤的最大深度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
