第二十八章 锐角三角函数预习自检卷(含解析)
文档属性
| 名称 | 第二十八章 锐角三角函数预习自检卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 11:03:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十八章锐角三角函数预习自检卷2023-2024学年数学九年级下册人教版
一、单选题
1.点关于原点对称的点的坐标是( )
A. B. C. D.
2.在中,,,点M是的中点,点P是上一点,与相交于点N,连接,若,则下列结论错误的是( )
A. B. C. D.
3.在坡度的山坡上种树,要求相邻两棵树之间的水平距离是6米,则斜坡上相邻两棵树之间的坡面距离是( )
A.6米 B.6.5米 C.13米 D.14.4米
4.如图,、分别是矩形的边、上点,且,,以边上点为圆心作,以边上点为圆心作,且所在的与所在的相切于点,若,,则的半径是( )
A. B. C. D.
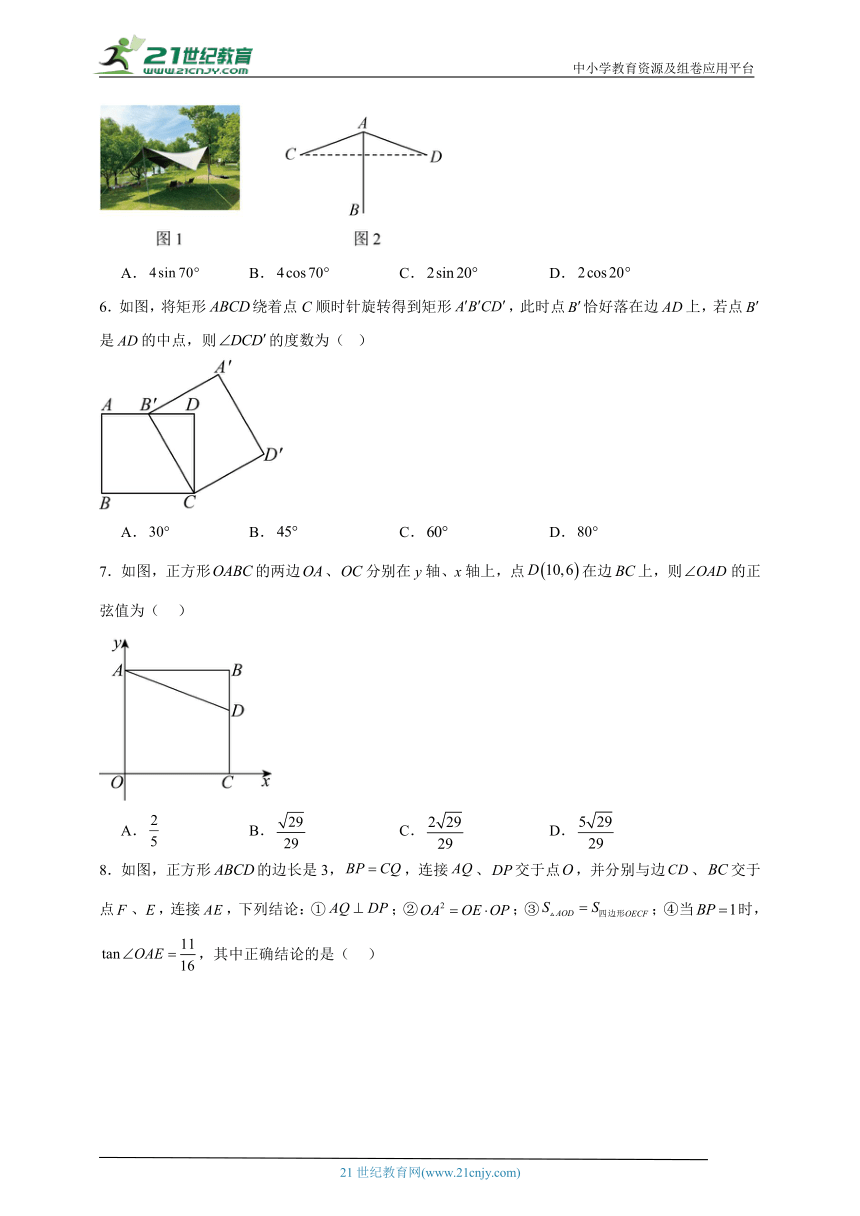
5.为争创全国文明城市,我市开展市容市貌整治行动,增加了许多市民露营地.某露营爱好者在营地搭建一种“天幕”(如图1),其截面示意图是轴对称图形(如图2),对称轴是垂直于地面的支杆所在的直线,撑开的遮阳部分用绳子拉直,分别记为,,且,的度数为,则此时“天幕”的宽度是单位:米)
A. B. C. D.
6.如图,将矩形绕着点C顺时针旋转得到矩形,此时点恰好落在边上,若点是的中点,则的度数为( )
A. B. C. D.
7.如图,正方形的两边、分别在y轴、x轴上,点在边上,则的正弦值为( )
A. B. C. D.
8.如图,正方形的边长是3,,连接、交于点,并分别与边、交于点、,连接,下列结论:①;②;③;④当时,,其中正确结论的是( )
A.①③④ B.①③ C.②④ D.①②④
二、填空题
9.如图,在菱形中,点是上的点,,若,,是边上的一个动点,则线段最小时,长为 .
10.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为 .
11.如图,在中,,点O是的中点,,,则的值为 .
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离,,则墙高 .
13.如图,在矩形中,,,P为边上一个动点,连接,将沿所在直线折叠后,点A的对应点落在点处,连接,则当取最小值时,的值为 .
14.如图,内接于,为的直径,的平分线交于点D,连接,.若,,则的长为 .
15.如图,扇形,点O为圆心,半径长为2,,再以点B为圆心,为半径作弧,交弧于点C,则阴影部分的面积是 .
16.如图,在正方形中,对角线相交于点O,点E是的中点,连接并延长交于点G,将线段绕点C逆时针旋转得到,连接,点H为的中点.连接,则的值为 .
三、解答题
17.计算:
18.“时代之舞,梦想领航”,合肥骆岗中央公园全向信标台成为合肥新地标.小丽同学想要通过测量及计算了解信标台的大致高度,如图1,当他步行至点A处,测得此时台顶C的仰角为,再步行20米至点B处,测得此时台顶C的仰角为(点A,B,D在同七、一条直线上),请帮小丽计算信标台的高度.(参考数据:,,,结果保留整数)
19.如图1,座落于福建省泉州市的中国闽台缘博物馆是一座反映中国大陆与宝岛台湾历史关系的国家级专题博物馆.小明为估测博物馆高度画出大致正面结构图.正面结构图如图2,为等腰三角形,为底边,四边形为矩形,于F,交于G,从点A至点B共行走440步,步长约为0.5米,测得,平台高约为13米,,求博物馆高的估算值.(结果按四舍五入保留到个位,参考数据:,,)
20.如图,在中,,以为直径的交于点,点在的延长线上,且.
(1)求证:直线是的切线;
(2)若,,求的半径长及的值.
21.如图是湖南师大附中博才实验中学湘江校区的钟楼,为了测量其高度,小明站在水平地面的点处,用测角仪测得钟楼顶部的仰角,测得钟楼底部的俯角,若测角仪距地面的高度.
(1)求测角仪到钟楼的距离(结果保留根号);
(2)求钟楼的高度(结果保留整数).(参考数据:,,,)
22.如图1,矩形中,,,点,分别为,边上任意一点,现将沿直线对折,点对应点为点.
(1)如图2,当,且点落在对角线上时,求线段的长;
(2)如图3,连接,,过点作,交于点.
①当为多少时,最长,并求出长的最大值;
②当,且点,,三点共线时,求的正切值;
(3)当时,的延长线交对角线于点,是否存在一点,使得以,,为顶点的三角形与相似,若存在,请直接写出线段的长;若不存在,请说明理由.
参考答案:
1.B
【分析】本题主要考查了求关于原点对称的点的坐标,求特殊角三角函数值,先求出点M的坐标,再根据关于原点对称的点横纵坐标对互为相反数进行求解即可.
【详解】解:∵点M的坐标为,即,
∴点关于原点对称的点的坐标是,
故选:B.
2.C
【分析】根据条件可得,进而得到,即可证明A;根据角之间的变换可证,设,进而表示出其他边长即可证明C、D.
【详解】解:如图,
∵点M是的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,故A正确;
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
设,则,,,,
∴,
解得:,
∴,
∴,,故C、D正确;
根据条件证不出,
故选:C.
【点睛】本题考查了相似三角形的判定与性质,勾股定理,等腰三角形的判定与性质等,根据题意正确画出图形是关键.
3.B
【分析】本题考查解直角三角形的应用,解题的关键是理解坡度的定义,学会利用勾股定理解决问题.根据坡度的定义,利用勾股定理即可解决问题.
【详解】解:如图,过作于,
山坡的坡度为,株距(相邻两棵树间的水平距离)是6米,
水平距离米,
,
铅垂高度米,
斜坡上相邻两树间的坡面距离(米,
故选:B.
4.A
【分析】本题主要考查了勾股定理、三角函数、分式方程、矩形的性质等知识点,熟练掌握相关知识是解题的关键.
如图:连接,,过点作于点,先根据四边形是矩形、和得到,进一步设,则,,并根据构造方程求出,,再设的半径为,的半径为,则,,,,在中根据勾股定理构造方程求出,得到,,最后证明四边形为矩形,进一步在中根据勾股定理构造关于的方程,求出的值即可.
【详解】解:如图,连接、,过点作于点,
与相切于点,
点在线段上
四边形是矩形,
,,,
,
,
,
,
设,则,
,
,
,解得,
经检验是分式方程的解,
,
设的半径为,的半径为,则,
,,,
,
,即,解得,
,,
,,
四边形为矩形,
,,
,
,
,即,解得,
的半径为.
故选:A.
5.A
【分析】本题考查了解直角三角形,三线合一的性质,根据正弦的定义,即可求解.
【详解】解:∵,对称轴是垂直于地面的支杆所在的直线,的度数为,
∴,
∵
∴
∴,
故选:A.
6.C
【分析】本题考查了旋转的性质,矩形的性质,解直角三角形,熟练掌握锐角三角函数的知识是解题的关键.由矩形的性质得,,由旋转的性质得,,然后利用锐角三角函数的知识即可求解.
【详解】解:∵四边形是矩形,
∴,.
由旋转的性质得,.
∵点是的中点,
∴.
∵,
∴,
∴.
故选C.
7.D
【分析】本题主要考查了求正弦值,由正方形性质和点可知正方形的边长为10,,,继而求出,由即可求解.
【详解】解:∵在正方形中,,
∴,
∵,
∴正方形的边长为10,即,,,
∴,
∴,
故选D.
8.B
【分析】由正方形的性质得到,证明, 得到,再证明,得到,故①正确;证明,得到.由于,则,进而得到,故②错误;证明, 推出.进而证明,故③正确;求出,由相似三角形的性质得到,则.证明,得到,即,故④错误.
【详解】解:∵四边形是正方形,
∴ .
∵ ,
∴.
在与中,
,
∴,
∴.
∵,
∴,
∴,
∴,故①正确;
∵,,
∴ ,
∴,
∴,
即.
∵,
∴,
∴,
∴,故②错误;
在与中,
,
∴,
∴,
∴.
在与中,
,
∴,
∴,
即,故③正确;
∵,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,即,故④错误.
故选:B.
【点睛】本题主要考查了正方形的性质,相似三角形的性质与判定,全等三角形的性质与判定,解直角三角形,熟知全等三角形的性质与判定,相似三角形的性质与判定是解题的关键.
9.
【分析】本题考查菱形的性质、解直角三角形、垂线段最短等知识.根据垂线段最短可知当时,线段最短.根据,只要求出、、、,即可解决问题.
【详解】解:根据垂线段最短可知当时,线段最短.
于,,
设,,则,,
,
,
,,,
当时,,
,
线段的最小值为,
.
故答案为:.
10./
【分析】本题考查了正弦函数的计算,如图,连接,得,从而得到,利用勾股定理计算即可.
【详解】如图,连接,
∵,
∴,
∴,
∵,
∴,
∴
∴,
∵,
∴,
故答案为:.
.
11.
【分析】本题考查了直角三角形的性质,勾股定理,正切,根据直角三角形斜边的中线等于斜边的一半即可得,在中,,,,根据勾股定理得,,即可得,掌握直角三角形的性质,勾股定理,正切是解题的关键.
【详解】解:∵在中,,点O是的中点,,
∴,
在中,,,,
根据勾股定理得,,
∴,
故答案为:.
12.
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,先解得到,再利用勾股定理求出的长即可.
【详解】解:由题意得,在中,,,,
∴,
∴,
故答案为:.
13./0.75
【分析】本题考查了折叠的性质、矩形的性质、解直角三角形等知识,根据折叠可得出,则在以B为圆心,为半径的圆上运动,则当B、、D三点共线时,取最小值,最小值为,然后在中利用正切的定义求解即可.
【详解】解:连接,
∵折叠,
∴,
∴在以B为圆心,为半径的圆上运动,
∵,
∴当B、、D三点共线时,取最小值,最小值为,
∴.
故答案为:.
14.
【分析】本题考查直径所对的圆周角是直角,勾股定理,解直角三角形,根据直径所对的圆周角是直角得到,然后利用勾股定理求出长,然后利用角平分线和圆周角定理得到,然后利用正弦计算是解题的关键.
【详解】解:∵为的直径,
∴,
∴,
又∵的平分线交于点D,
∴,
∴,
∴,
故答案为:.
15.
【分析】此题考查了求不规则图图形的面积,扇形的面积公式,等边三角形的判定和性质,正确理解图形作出辅助线及正确掌握扇形的面积公式是解题的关键.
连接,,过点作于点,推出是等边三角形,得到,利用三角函数求出的长,根据公式求出,,,的值即可得到答案.
【详解】解:连接,,过点作于点,
在扇形中,,,以为圆心,为半径画弧,交弧于点,
,
是等边三角形,
,
,
,
,,,
,
图中阴影部分的面积为:.
故答案为:.
16.
【分析】如图,连接,则,由旋转的性质可知,,,则,,证明,则,即,设,则,由勾股定理得,,根据,计算求解即可.
【详解】解:如图,连接,
∵正方形,
∴,,,,,
∴,
由旋转的性质可知,,,
∵点H为的中点,
∴,
∴,
∴,即,
∵,,
∴,
∴,即,
设,则,
由勾股定理得,,
∴,
故答案为:.
【点睛】本题考查了正方形的性质,旋转的性质,相似三角形的判定与性质,余弦,勾股定理,等腰三角形的判定与性质等知识.熟练掌握正方形的性质,旋转的性质,相似三角形的判定与性质,余弦,勾股定理,等腰三角形的判定与性质是解题的关键.
17.
【分析】本题考查了绝对值的性质,特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
先进行绝对值的化简,代入特殊角的三角函数值运算,然后合并即可.
【详解】解:
.
18.信标台的高约为60米
【分析】本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.在中,由锐角三角函数定义可得,再在中,由锐角三角函数定义可得,进而可得的高度.
【详解】解:设米,
在中,,
∴米,
在中,,
∴,
∵,米,
∴,
解得.
答:信标台的高约为60米.
19.米
【分析】本题主要考查解直角三角形的应用,根据等腰三角形的性质出米,通过解直角三角形求出米,再加上的长即可得出结论.
【详解】解:从点A至点B共行走440步,步长约为0.5米,
米
于F,是为底边的等腰三角形,
,,
米
,,
,
∴米
(米)
即博物馆高约为43米.
20.(1)见解析
(2)的半径为;
【分析】(1)根据圆周角定理以及等腰三角形的性质可得是角平分线,进而得出,由三角形的内角和定理得出即可;
(2)过点作,垂足为,由锐角三角函数可求出进而得出半径的值,再根据平行线分线段成比例,求出,,由锐角三角函数的定义求出答案即可.
【详解】(1)证明:如图,连接,
是的直径,
,即,
,
,
平分,即,
,
,
,
,
,
即,
是的半径,
是的切线;
(2)解:过点作,垂足为,
,
由可得,
,
,
,
即的半径为;
,,
,
,
,
,
,
,,
,
.
【点睛】本题考查切线的判定,锐角三角函数,圆周角定理以及平行线分线段成比例,掌握切线的判定方法,锐角三角函数的定义以及圆周角定理是解题的关键.
21.(1)
(2)钟楼的高度约为
【分析】本题考查了解直角三角形的应用;
(1)根据平行线的性质得出,根据,即可求解.
(2)依题意四边形为矩形,解得出,进而根据,即可求解.
【详解】(1)∵,
∴
∴
又∵,∴
∴.
(2)解:依题意,
∴四边形为矩形
∴,
中,,
即:
∴
∴钟楼的高度约为.
22.(1)5
(2)①当时,最长,最长为;②
(3)或
【分析】(1)连接,首先证明,利用勾股定理求出,进而得到,再证明,得到,进一步证明,则;
(2)①设,则,证明,得到,可得,得到,则当时,最长,最长为;
②当时,此时点,,三点共线,证明,得到,设,则,,,由勾股定理得到,再由,得到,解得,据此可得答案.
(3)分两种情形:当时,如图,过点作于.当时,如图,过点作交于点,过点作于,过点作于,分别求解即可.
【详解】(1)解:连接,如图2所示,
由折叠得:,,
∵,
∴,
∵在矩形中,,,
∴,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:①设,则,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴,
∴,即,
∴,
∴当时,有最大值,
∴当时,最长,最长为;
②当时,此时点,,三点共线,
∵,
∴,
∴,
设,则,,,
在中,,即,
∵,
∴,
解得,
∴,
∴;
(3)解:当时,如图,过点作于,
由折叠的性质可得,,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
设,则,,,
∴,
∵,
∴
∴,
∴,
解得:,
∴.
当时,如图,过点作交于点,过点作于,过点作于,
设,则,
由折叠的性质可得,
同理可证明,
∴,
同理可得
设,
∴,,,
∴①,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴②,
联立①②
解得,
∴,
综上所述,满足条件的的值为或.
【点睛】本题属于相似形综合题,考查了矩形的性质,相似三角形的判定和性质,解直角三角形,勾股定理,二次函数的最值问题等知识,解题的关键是学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十八章锐角三角函数预习自检卷2023-2024学年数学九年级下册人教版
一、单选题
1.点关于原点对称的点的坐标是( )
A. B. C. D.
2.在中,,,点M是的中点,点P是上一点,与相交于点N,连接,若,则下列结论错误的是( )
A. B. C. D.
3.在坡度的山坡上种树,要求相邻两棵树之间的水平距离是6米,则斜坡上相邻两棵树之间的坡面距离是( )
A.6米 B.6.5米 C.13米 D.14.4米
4.如图,、分别是矩形的边、上点,且,,以边上点为圆心作,以边上点为圆心作,且所在的与所在的相切于点,若,,则的半径是( )
A. B. C. D.
5.为争创全国文明城市,我市开展市容市貌整治行动,增加了许多市民露营地.某露营爱好者在营地搭建一种“天幕”(如图1),其截面示意图是轴对称图形(如图2),对称轴是垂直于地面的支杆所在的直线,撑开的遮阳部分用绳子拉直,分别记为,,且,的度数为,则此时“天幕”的宽度是单位:米)
A. B. C. D.
6.如图,将矩形绕着点C顺时针旋转得到矩形,此时点恰好落在边上,若点是的中点,则的度数为( )
A. B. C. D.
7.如图,正方形的两边、分别在y轴、x轴上,点在边上,则的正弦值为( )
A. B. C. D.
8.如图,正方形的边长是3,,连接、交于点,并分别与边、交于点、,连接,下列结论:①;②;③;④当时,,其中正确结论的是( )
A.①③④ B.①③ C.②④ D.①②④
二、填空题
9.如图,在菱形中,点是上的点,,若,,是边上的一个动点,则线段最小时,长为 .
10.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为 .
11.如图,在中,,点O是的中点,,,则的值为 .
12.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离,,则墙高 .
13.如图,在矩形中,,,P为边上一个动点,连接,将沿所在直线折叠后,点A的对应点落在点处,连接,则当取最小值时,的值为 .
14.如图,内接于,为的直径,的平分线交于点D,连接,.若,,则的长为 .
15.如图,扇形,点O为圆心,半径长为2,,再以点B为圆心,为半径作弧,交弧于点C,则阴影部分的面积是 .
16.如图,在正方形中,对角线相交于点O,点E是的中点,连接并延长交于点G,将线段绕点C逆时针旋转得到,连接,点H为的中点.连接,则的值为 .
三、解答题
17.计算:
18.“时代之舞,梦想领航”,合肥骆岗中央公园全向信标台成为合肥新地标.小丽同学想要通过测量及计算了解信标台的大致高度,如图1,当他步行至点A处,测得此时台顶C的仰角为,再步行20米至点B处,测得此时台顶C的仰角为(点A,B,D在同七、一条直线上),请帮小丽计算信标台的高度.(参考数据:,,,结果保留整数)
19.如图1,座落于福建省泉州市的中国闽台缘博物馆是一座反映中国大陆与宝岛台湾历史关系的国家级专题博物馆.小明为估测博物馆高度画出大致正面结构图.正面结构图如图2,为等腰三角形,为底边,四边形为矩形,于F,交于G,从点A至点B共行走440步,步长约为0.5米,测得,平台高约为13米,,求博物馆高的估算值.(结果按四舍五入保留到个位,参考数据:,,)
20.如图,在中,,以为直径的交于点,点在的延长线上,且.
(1)求证:直线是的切线;
(2)若,,求的半径长及的值.
21.如图是湖南师大附中博才实验中学湘江校区的钟楼,为了测量其高度,小明站在水平地面的点处,用测角仪测得钟楼顶部的仰角,测得钟楼底部的俯角,若测角仪距地面的高度.
(1)求测角仪到钟楼的距离(结果保留根号);
(2)求钟楼的高度(结果保留整数).(参考数据:,,,)
22.如图1,矩形中,,,点,分别为,边上任意一点,现将沿直线对折,点对应点为点.
(1)如图2,当,且点落在对角线上时,求线段的长;
(2)如图3,连接,,过点作,交于点.
①当为多少时,最长,并求出长的最大值;
②当,且点,,三点共线时,求的正切值;
(3)当时,的延长线交对角线于点,是否存在一点,使得以,,为顶点的三角形与相似,若存在,请直接写出线段的长;若不存在,请说明理由.
参考答案:
1.B
【分析】本题主要考查了求关于原点对称的点的坐标,求特殊角三角函数值,先求出点M的坐标,再根据关于原点对称的点横纵坐标对互为相反数进行求解即可.
【详解】解:∵点M的坐标为,即,
∴点关于原点对称的点的坐标是,
故选:B.
2.C
【分析】根据条件可得,进而得到,即可证明A;根据角之间的变换可证,设,进而表示出其他边长即可证明C、D.
【详解】解:如图,
∵点M是的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,故A正确;
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
设,则,,,,
∴,
解得:,
∴,
∴,,故C、D正确;
根据条件证不出,
故选:C.
【点睛】本题考查了相似三角形的判定与性质,勾股定理,等腰三角形的判定与性质等,根据题意正确画出图形是关键.
3.B
【分析】本题考查解直角三角形的应用,解题的关键是理解坡度的定义,学会利用勾股定理解决问题.根据坡度的定义,利用勾股定理即可解决问题.
【详解】解:如图,过作于,
山坡的坡度为,株距(相邻两棵树间的水平距离)是6米,
水平距离米,
,
铅垂高度米,
斜坡上相邻两树间的坡面距离(米,
故选:B.
4.A
【分析】本题主要考查了勾股定理、三角函数、分式方程、矩形的性质等知识点,熟练掌握相关知识是解题的关键.
如图:连接,,过点作于点,先根据四边形是矩形、和得到,进一步设,则,,并根据构造方程求出,,再设的半径为,的半径为,则,,,,在中根据勾股定理构造方程求出,得到,,最后证明四边形为矩形,进一步在中根据勾股定理构造关于的方程,求出的值即可.
【详解】解:如图,连接、,过点作于点,
与相切于点,
点在线段上
四边形是矩形,
,,,
,
,
,
,
设,则,
,
,
,解得,
经检验是分式方程的解,
,
设的半径为,的半径为,则,
,,,
,
,即,解得,
,,
,,
四边形为矩形,
,,
,
,
,即,解得,
的半径为.
故选:A.
5.A
【分析】本题考查了解直角三角形,三线合一的性质,根据正弦的定义,即可求解.
【详解】解:∵,对称轴是垂直于地面的支杆所在的直线,的度数为,
∴,
∵
∴
∴,
故选:A.
6.C
【分析】本题考查了旋转的性质,矩形的性质,解直角三角形,熟练掌握锐角三角函数的知识是解题的关键.由矩形的性质得,,由旋转的性质得,,然后利用锐角三角函数的知识即可求解.
【详解】解:∵四边形是矩形,
∴,.
由旋转的性质得,.
∵点是的中点,
∴.
∵,
∴,
∴.
故选C.
7.D
【分析】本题主要考查了求正弦值,由正方形性质和点可知正方形的边长为10,,,继而求出,由即可求解.
【详解】解:∵在正方形中,,
∴,
∵,
∴正方形的边长为10,即,,,
∴,
∴,
故选D.
8.B
【分析】由正方形的性质得到,证明, 得到,再证明,得到,故①正确;证明,得到.由于,则,进而得到,故②错误;证明, 推出.进而证明,故③正确;求出,由相似三角形的性质得到,则.证明,得到,即,故④错误.
【详解】解:∵四边形是正方形,
∴ .
∵ ,
∴.
在与中,
,
∴,
∴.
∵,
∴,
∴,
∴,故①正确;
∵,,
∴ ,
∴,
∴,
即.
∵,
∴,
∴,
∴,故②错误;
在与中,
,
∴,
∴,
∴.
在与中,
,
∴,
∴,
即,故③正确;
∵,
∴.
∵,
∴,
∴,
∴.
∵,
∴,
∴,即,故④错误.
故选:B.
【点睛】本题主要考查了正方形的性质,相似三角形的性质与判定,全等三角形的性质与判定,解直角三角形,熟知全等三角形的性质与判定,相似三角形的性质与判定是解题的关键.
9.
【分析】本题考查菱形的性质、解直角三角形、垂线段最短等知识.根据垂线段最短可知当时,线段最短.根据,只要求出、、、,即可解决问题.
【详解】解:根据垂线段最短可知当时,线段最短.
于,,
设,,则,,
,
,
,,,
当时,,
,
线段的最小值为,
.
故答案为:.
10./
【分析】本题考查了正弦函数的计算,如图,连接,得,从而得到,利用勾股定理计算即可.
【详解】如图,连接,
∵,
∴,
∴,
∵,
∴,
∴
∴,
∵,
∴,
故答案为:.
.
11.
【分析】本题考查了直角三角形的性质,勾股定理,正切,根据直角三角形斜边的中线等于斜边的一半即可得,在中,,,,根据勾股定理得,,即可得,掌握直角三角形的性质,勾股定理,正切是解题的关键.
【详解】解:∵在中,,点O是的中点,,
∴,
在中,,,,
根据勾股定理得,,
∴,
故答案为:.
12.
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,先解得到,再利用勾股定理求出的长即可.
【详解】解:由题意得,在中,,,,
∴,
∴,
故答案为:.
13./0.75
【分析】本题考查了折叠的性质、矩形的性质、解直角三角形等知识,根据折叠可得出,则在以B为圆心,为半径的圆上运动,则当B、、D三点共线时,取最小值,最小值为,然后在中利用正切的定义求解即可.
【详解】解:连接,
∵折叠,
∴,
∴在以B为圆心,为半径的圆上运动,
∵,
∴当B、、D三点共线时,取最小值,最小值为,
∴.
故答案为:.
14.
【分析】本题考查直径所对的圆周角是直角,勾股定理,解直角三角形,根据直径所对的圆周角是直角得到,然后利用勾股定理求出长,然后利用角平分线和圆周角定理得到,然后利用正弦计算是解题的关键.
【详解】解:∵为的直径,
∴,
∴,
又∵的平分线交于点D,
∴,
∴,
∴,
故答案为:.
15.
【分析】此题考查了求不规则图图形的面积,扇形的面积公式,等边三角形的判定和性质,正确理解图形作出辅助线及正确掌握扇形的面积公式是解题的关键.
连接,,过点作于点,推出是等边三角形,得到,利用三角函数求出的长,根据公式求出,,,的值即可得到答案.
【详解】解:连接,,过点作于点,
在扇形中,,,以为圆心,为半径画弧,交弧于点,
,
是等边三角形,
,
,
,
,,,
,
图中阴影部分的面积为:.
故答案为:.
16.
【分析】如图,连接,则,由旋转的性质可知,,,则,,证明,则,即,设,则,由勾股定理得,,根据,计算求解即可.
【详解】解:如图,连接,
∵正方形,
∴,,,,,
∴,
由旋转的性质可知,,,
∵点H为的中点,
∴,
∴,
∴,即,
∵,,
∴,
∴,即,
设,则,
由勾股定理得,,
∴,
故答案为:.
【点睛】本题考查了正方形的性质,旋转的性质,相似三角形的判定与性质,余弦,勾股定理,等腰三角形的判定与性质等知识.熟练掌握正方形的性质,旋转的性质,相似三角形的判定与性质,余弦,勾股定理,等腰三角形的判定与性质是解题的关键.
17.
【分析】本题考查了绝对值的性质,特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
先进行绝对值的化简,代入特殊角的三角函数值运算,然后合并即可.
【详解】解:
.
18.信标台的高约为60米
【分析】本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.在中,由锐角三角函数定义可得,再在中,由锐角三角函数定义可得,进而可得的高度.
【详解】解:设米,
在中,,
∴米,
在中,,
∴,
∵,米,
∴,
解得.
答:信标台的高约为60米.
19.米
【分析】本题主要考查解直角三角形的应用,根据等腰三角形的性质出米,通过解直角三角形求出米,再加上的长即可得出结论.
【详解】解:从点A至点B共行走440步,步长约为0.5米,
米
于F,是为底边的等腰三角形,
,,
米
,,
,
∴米
(米)
即博物馆高约为43米.
20.(1)见解析
(2)的半径为;
【分析】(1)根据圆周角定理以及等腰三角形的性质可得是角平分线,进而得出,由三角形的内角和定理得出即可;
(2)过点作,垂足为,由锐角三角函数可求出进而得出半径的值,再根据平行线分线段成比例,求出,,由锐角三角函数的定义求出答案即可.
【详解】(1)证明:如图,连接,
是的直径,
,即,
,
,
平分,即,
,
,
,
,
,
即,
是的半径,
是的切线;
(2)解:过点作,垂足为,
,
由可得,
,
,
,
即的半径为;
,,
,
,
,
,
,
,,
,
.
【点睛】本题考查切线的判定,锐角三角函数,圆周角定理以及平行线分线段成比例,掌握切线的判定方法,锐角三角函数的定义以及圆周角定理是解题的关键.
21.(1)
(2)钟楼的高度约为
【分析】本题考查了解直角三角形的应用;
(1)根据平行线的性质得出,根据,即可求解.
(2)依题意四边形为矩形,解得出,进而根据,即可求解.
【详解】(1)∵,
∴
∴
又∵,∴
∴.
(2)解:依题意,
∴四边形为矩形
∴,
中,,
即:
∴
∴钟楼的高度约为.
22.(1)5
(2)①当时,最长,最长为;②
(3)或
【分析】(1)连接,首先证明,利用勾股定理求出,进而得到,再证明,得到,进一步证明,则;
(2)①设,则,证明,得到,可得,得到,则当时,最长,最长为;
②当时,此时点,,三点共线,证明,得到,设,则,,,由勾股定理得到,再由,得到,解得,据此可得答案.
(3)分两种情形:当时,如图,过点作于.当时,如图,过点作交于点,过点作于,过点作于,分别求解即可.
【详解】(1)解:连接,如图2所示,
由折叠得:,,
∵,
∴,
∵在矩形中,,,
∴,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:①设,则,
∵四边形是矩形,
∴,
∵,
∴,
∴,
∴,
∴,
∴,即,
∴,
∴当时,有最大值,
∴当时,最长,最长为;
②当时,此时点,,三点共线,
∵,
∴,
∴,
设,则,,,
在中,,即,
∵,
∴,
解得,
∴,
∴;
(3)解:当时,如图,过点作于,
由折叠的性质可得,,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
设,则,,,
∴,
∵,
∴
∴,
∴,
解得:,
∴.
当时,如图,过点作交于点,过点作于,过点作于,
设,则,
由折叠的性质可得,
同理可证明,
∴,
同理可得
设,
∴,,,
∴①,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴②,
联立①②
解得,
∴,
综上所述,满足条件的的值为或.
【点睛】本题属于相似形综合题,考查了矩形的性质,相似三角形的判定和性质,解直角三角形,勾股定理,二次函数的最值问题等知识,解题的关键是学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
