人教版数学八年级下册18.2.2.2 菱形的判定同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.2.2 菱形的判定同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 97.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 11:44:49 | ||
图片预览


文档简介
第十八章 平行四边形
18.2.2 菱形
第2课时 菱形的判定
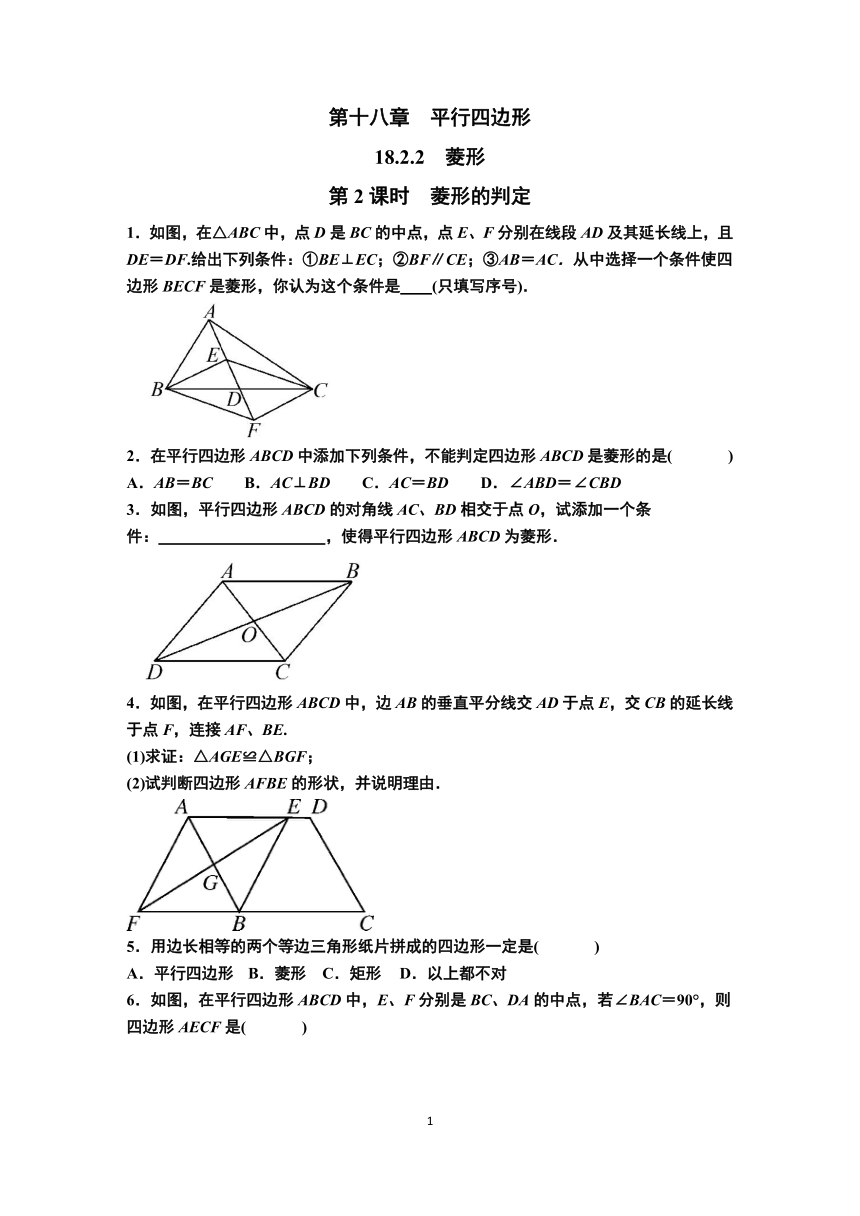
1.如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.如图,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: ,使得平行四边形ABCD为菱形.
4.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
5.用边长相等的两个等边三角形纸片拼成的四边形一定是( )
A.平行四边形 B.菱形 C.矩形 D.以上都不对
6.如图,在平行四边形ABCD中,E、F分别是BC、DA的中点,若∠BAC=90°,则四边形AECF是( )
A.矩形 B.菱形 C.平行四边形 D.不能确定
7.下列命题正确的是( )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形 D.对角线互相垂直的平行四边形是菱形
8.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( )
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
9.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
10.如图,在△ABC中,AD⊥BC于D,E、F分别是AB、AC边的中点,连接DE、EF、FD,当△ABC满足 条件时,四边形AEDF是菱形(填一个你认为恰当的条件即可).
11.在四边形ABCD中,给出四个条件:①AB=CD;②AD∥BC;③AC⊥BD;④AC平分∠BAD.由其中三个条件可推出四边形ABCD是菱形,你认为这三个条件是 (不能写四个条件,只需填序号).
12.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在 ABCD中,对角线AC、BD交于点O, .求证: .
13.如图,矩形ABCD中 ,AB=4,BC=2,点E、F分别在AB、CD上,且BE=DF=.
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
14.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
1
参考答案
1. ③
2. C
3. AC⊥BD或AB=AD
4. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEG=∠BFG,∵EF垂直平分AB,∴AG=BG,在△AGE和△BGF中,∠AEG=∠BFG,∠AGE=∠BGF,AG=BG,∴△AGE≌△BGF(AAS);
(2)解:四边形AFBE是菱形,理由如下:∵△AGE≌△BGF,∴AE=BF,∵AD∥BC,∴四边形AFBE是平行四边形,又∵EF⊥AB,∴四边形AFBE是菱形.
5-9 BBDBA
10. AB=AC或BD=CD
11. ①③④或②③④
12. AC⊥BD 四边形ABCD是菱形
证明:∵四边形ABCD为平行四边形,∴BO=DO,∵AC⊥BD,∴AC垂直平分BD,∴AB=AD,∴四边形ABCD为菱形.
13. (1)证明:矩形ABCD中,AB平行且等于CD,∵BE=DF,∴AE平行且等于CF,∴四边形AECF是平行四边形,又∵BE=DF=,AB=4,∴AE=AB-BE=,在Rt△BCE中,CE2=BE2+BC2,CE2=()2+22,∴CE=,∴CE=AE,∴平行四边形AECF是菱形;
(2)解:连接AC,交EF于点O,在Rt△ABC中,AB=4,BC=2,∴AC==2,∵AC·EF·=AE·BC,∴2×EF×=×2,∴EF=.
14. (1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
18.2.2 菱形
第2课时 菱形的判定
1.如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.如图,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: ,使得平行四边形ABCD为菱形.
4.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
5.用边长相等的两个等边三角形纸片拼成的四边形一定是( )
A.平行四边形 B.菱形 C.矩形 D.以上都不对
6.如图,在平行四边形ABCD中,E、F分别是BC、DA的中点,若∠BAC=90°,则四边形AECF是( )
A.矩形 B.菱形 C.平行四边形 D.不能确定
7.下列命题正确的是( )
A.对角线相等的四边形是菱形 B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形 D.对角线互相垂直的平行四边形是菱形
8.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( )
A.一组邻边相等的四边形是菱形
B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
9.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
10.如图,在△ABC中,AD⊥BC于D,E、F分别是AB、AC边的中点,连接DE、EF、FD,当△ABC满足 条件时,四边形AEDF是菱形(填一个你认为恰当的条件即可).
11.在四边形ABCD中,给出四个条件:①AB=CD;②AD∥BC;③AC⊥BD;④AC平分∠BAD.由其中三个条件可推出四边形ABCD是菱形,你认为这三个条件是 (不能写四个条件,只需填序号).
12.求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在 ABCD中,对角线AC、BD交于点O, .求证: .
13.如图,矩形ABCD中 ,AB=4,BC=2,点E、F分别在AB、CD上,且BE=DF=.
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
14.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
1
参考答案
1. ③
2. C
3. AC⊥BD或AB=AD
4. (1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEG=∠BFG,∵EF垂直平分AB,∴AG=BG,在△AGE和△BGF中,∠AEG=∠BFG,∠AGE=∠BGF,AG=BG,∴△AGE≌△BGF(AAS);
(2)解:四边形AFBE是菱形,理由如下:∵△AGE≌△BGF,∴AE=BF,∵AD∥BC,∴四边形AFBE是平行四边形,又∵EF⊥AB,∴四边形AFBE是菱形.
5-9 BBDBA
10. AB=AC或BD=CD
11. ①③④或②③④
12. AC⊥BD 四边形ABCD是菱形
证明:∵四边形ABCD为平行四边形,∴BO=DO,∵AC⊥BD,∴AC垂直平分BD,∴AB=AD,∴四边形ABCD为菱形.
13. (1)证明:矩形ABCD中,AB平行且等于CD,∵BE=DF,∴AE平行且等于CF,∴四边形AECF是平行四边形,又∵BE=DF=,AB=4,∴AE=AB-BE=,在Rt△BCE中,CE2=BE2+BC2,CE2=()2+22,∴CE=,∴CE=AE,∴平行四边形AECF是菱形;
(2)解:连接AC,交EF于点O,在Rt△ABC中,AB=4,BC=2,∴AC==2,∵AC·EF·=AE·BC,∴2×EF×=×2,∴EF=.
14. (1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
