17.1 勾股定理同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
17.1 勾股定理
一、单选题
1.在直角 中, ,如果 , ,那么 的长是( )
A.2 B.5 C. D.5或
2. 若一个直角三角形的两条直角边长分别是6和8,则斜边长是( )
A.6 B.7 C.8 D.10
3.已知直角三角形的两直角边长分别为3和4,则斜边上的高为( )
A.5 B.3 C. D.
二、填空题
4.在 中, , , ,则 .
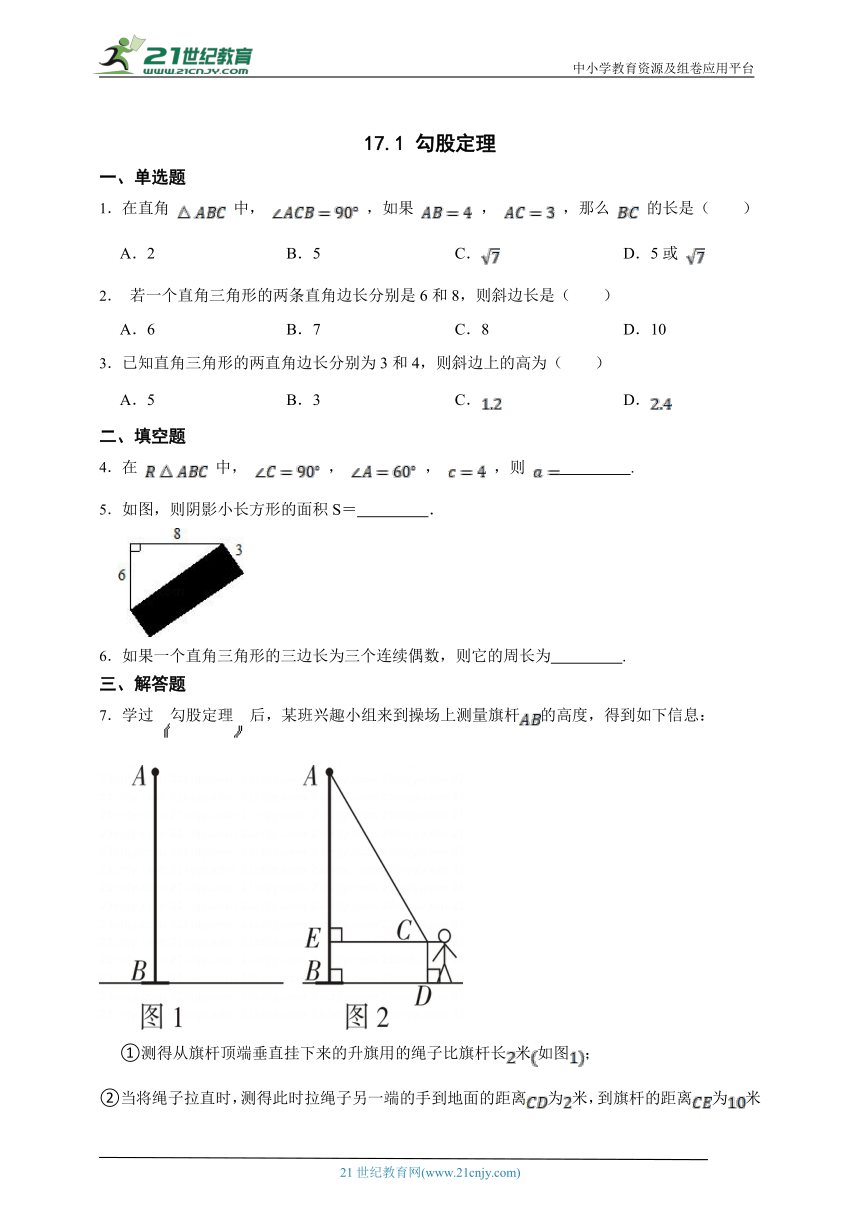
5.如图,则阴影小长方形的面积S= .
6.如果一个直角三角形的三边长为三个连续偶数,则它的周长为 .
三、解答题
7.学过勾股定理后,某班兴趣小组来到操场上测量旗杆的高度,得到如下信息:
①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长米如图;
②当将绳子拉直时,测得此时拉绳子另一端的手到地面的距离为米,到旗杆的距离为米如图.根据以上信息,求旗杆的高度.
8.如图所示是一块菜地,已知AD=8 m,CD=6 m,∠D=90°,AB=26 m,BC=24 m,求这块菜地的面积.
四、综合题
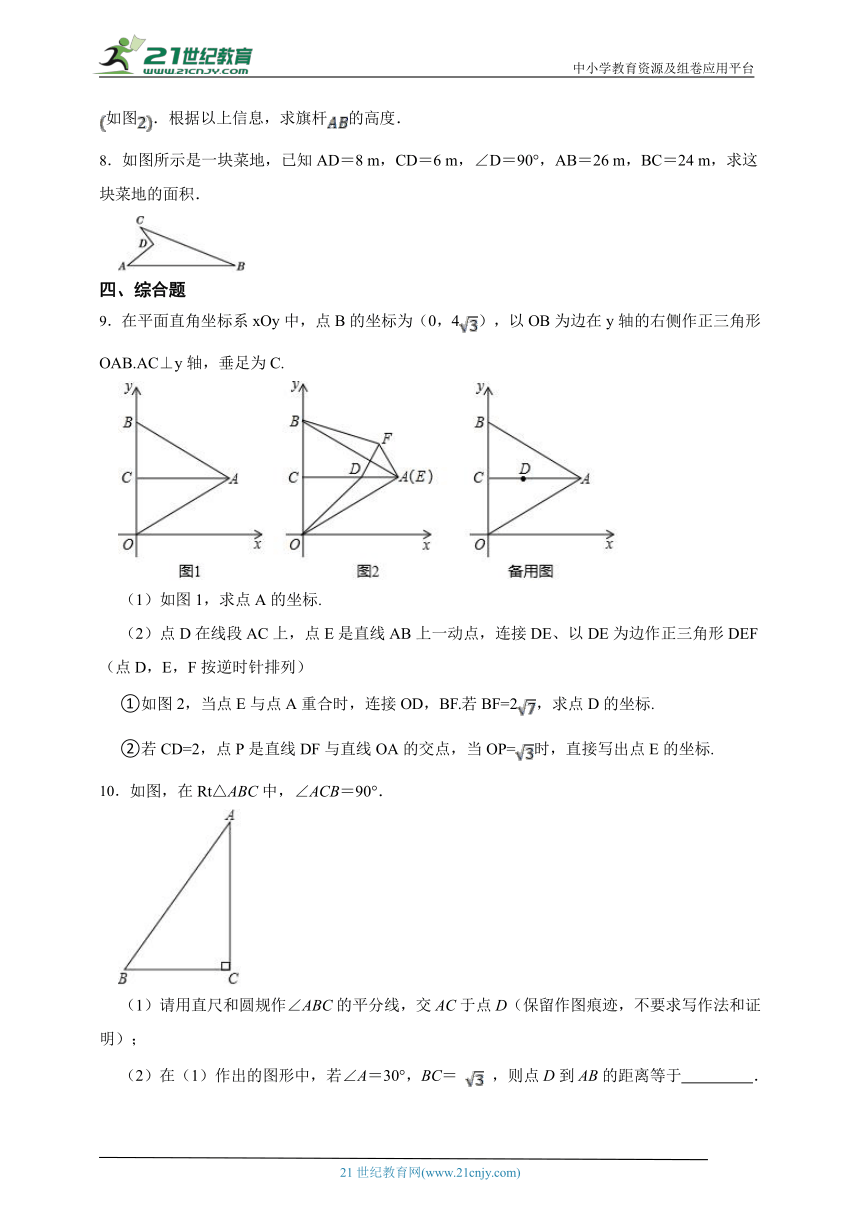
9.在平面直角坐标系xOy中,点B的坐标为(0,4),以OB为边在y轴的右侧作正三角形OAB.AC⊥y轴,垂足为C.
(1)如图1,求点A的坐标.
(2)点D在线段AC上,点E是直线AB上一动点,连接DE、以DE为边作正三角形DEF(点D,E,F按逆时针排列)
①如图2,当点E与点A重合时,连接OD,BF.若BF=2,求点D的坐标.
②若CD=2,点P是直线DF与直线OA的交点,当OP=时,直接写出点E的坐标.
10.如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);
(2)在(1)作出的图形中,若∠A=30°,BC= ,则点D到AB的距离等于 .
答案解析部分
1.【答案】C
【解析】【解答】解:∵∠ACB=90°,
则AB为斜边,
∴BC= = ,
故答案为:C.
【分析】根据∠ACB=90°得出AB为斜边,再用勾股定理求解.
2.【答案】D
【解析】【解答】解:∵一个直角三角形的两条直角边长分别是6和8,
∴斜边长为:,
故答案为:D.
【分析】根据题意利用勾股定理计算求解即可。
3.【答案】D
【解析】【解答】解:设斜边上的高为h,
由勾股定理得,三角形的斜边长= ,
则 ,
解得,h=2.4,
故答案为:D.
【分析】根据勾股定理求出斜边的边长,在应用等积法即可求得斜边上的高.
4.【答案】
【解析】【解答】解: , , ,
,
,
,
故答案为: .
【分析】利用直角三角形30度角的性质求出b,再利用勾股定理求出a即可.
5.【答案】30
【解析】【解答】由勾股定理得: =10,
∴阴影小长方形的面积S=3×10=30;
故答案是:30.
【分析】由勾股定理求出小长方形的长,再由长方形的面积公式进行计算.
6.【答案】24
【解析】【解答】设三边长分别为:
根据勾股定理可得:
解得: (不符合题意,舍去)
三角形的三边长分别为:
则周长为:
故答案为:24.
【分析】由题意可设三边长分别为:2n-2,2n,2n+2,根据勾股定理可得关于n的方程,解方程可求得三角形的各边长,再根据三角形的周长=三角形三边之和可求解.
7.【答案】解:设米,
则,,
,
,
即:,
,
,
.
答:旗杆的高度为米.
【解析】【分析】利用勾股定理列方程求出 , 再解方程即可。
8.【答案】解:如图所示,连接AC,
∵∠D=90°,
∴AC2=AD2+CD2,
∴AC=10,
又∵AC2+BC2=676,AB2=262=676,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ABC-S△ACD=
【解析】【分析】根据题意,连接AC,根据题意可得出△ABC为直角三角形,利用两个三角形的面积差,可得出菜地面积。
9.【答案】(1)解:∵点B的坐标为(0,4),△OAB是正三角形,且AC⊥y轴,
∴AC是边OB的中线,
∴C(0,2),
在Rt△ACO中,AO=4,CO=2,
由勾股定理可得,AC=6,
∴A(6,2).
(2)解:①AF=AD,AB=AO,
∵△OAB和△DEF是正三角形,
∴∠CAF=∠OAB=60°,
∵∠BAF=∠CAF-60°,∠OAD=∠OB-60°,
∴∠BAF=∠OAD,
在△BAF和△OAD中,
,
∴△BAF≌△OAD(SAS),
∴OD=BF=2,
∵OC=2,
∴CD=4,
∴D(4,2);
②(,)或(,).
【解析】【解答】解:(2)②当点P在x轴下方时,如图,连接OD,过点E作AC的垂线,交CA的延长线于点G,
则∠GAE=30°,
在Rt△ODC中,∠OCD=90°,CD=2,OC=2,
∴OD=4,∠COD=30°,
∴AD=OD=4,
∵∠AOC=60°,
∴∠AOD=30°
∴∠DOP=150°,
∵∠GAE=∠BAC=30°,
∴∠DOP=∠DAE=150°,
∵∠CDO=∠EDF=60°,
∴∠ODA=∠EDP=120°,
∴∠ODA-∠DOE=∠EDP-∠DOE
∴∠PDO=∠EDA,
∴△PDO≌△EDA(ASA),
∴OP=AE,
∴GE,AG,
∵A(6,2),
∴E(,);
当点P在x轴上方时,如图,连接OD,过点E作EG⊥AC于点G,
同上可知,△P′DO≌△EDA(ASA),
∴OP=AE,
∴GE,AG,
∵A(6,2),
∴E(,);
综上可知,点E的坐标为(,)或(,).
【分析】(1)根据等边三角形的性质结合点B的坐标可得C(0,2),在Rt△ACO中,根据勾股定理可得AC的值,进而可得点A的坐标;
(2)①由正三角形的性质可得∠CAF=∠OAB=60°,结合角的和差关系可得∠BAF=∠OAD,证明△BAF≌△OAD,得到OD=BF=2,利用勾股定理可得CD,进而可得点D的坐标;
②当点P在x轴下方时,连接OD,过点E作AC的垂线,交CA的延长线于点G,则∠GAE=30°,易得OD=4,∠COD=30°,AD=OD=4,证明△PDO≌△EDA,得到OP=AE,然后求出GE、AG,结合点A的坐标就可求出点E的坐标;当点P在x轴上方时,连接OD,过点E作EG⊥AC于点G,
同上可知△P′DO≌△EDA,OP=AE,同理可得点E的坐标.
10.【答案】(1)解:如图所示,BD即为所求;
(2)1
【解析】【解答】解:(1)如图所示,BD即为所求;
;(2)设DC=x,
过点D作DE⊥AB于E,
则∠DEB=∠C=90°,
∵BD平分∠ABC,
∴DE=DC=x,
∵∠A=30°,BC= ,
∴AD=2DE=2x,AB=2BC=2 ,
由BC2+AC2=AB2得( )2+(3x)2=(2 )2,
解得:x=1(负值舍去),
∴DE=1,即点D到AB的距离等于1,
故答案为:1.
【分析】(1)根据角平分线的作法和步骤作图即可;
(2)设DC=x,过点D作DE⊥AB于E,根据角平线的性质可知DE=DC=x,根据直角三角形中30°所对的直角边等于斜边的一半,可知AD=2DE=2x,AB=2BC=2,由勾股定理易知BC2+AC2=AB2,即()2+(3x)2=(2)2,从而得解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
17.1 勾股定理
一、单选题
1.在直角 中, ,如果 , ,那么 的长是( )
A.2 B.5 C. D.5或
2. 若一个直角三角形的两条直角边长分别是6和8,则斜边长是( )
A.6 B.7 C.8 D.10
3.已知直角三角形的两直角边长分别为3和4,则斜边上的高为( )
A.5 B.3 C. D.
二、填空题
4.在 中, , , ,则 .
5.如图,则阴影小长方形的面积S= .
6.如果一个直角三角形的三边长为三个连续偶数,则它的周长为 .
三、解答题
7.学过勾股定理后,某班兴趣小组来到操场上测量旗杆的高度,得到如下信息:
①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长米如图;
②当将绳子拉直时,测得此时拉绳子另一端的手到地面的距离为米,到旗杆的距离为米如图.根据以上信息,求旗杆的高度.
8.如图所示是一块菜地,已知AD=8 m,CD=6 m,∠D=90°,AB=26 m,BC=24 m,求这块菜地的面积.
四、综合题
9.在平面直角坐标系xOy中,点B的坐标为(0,4),以OB为边在y轴的右侧作正三角形OAB.AC⊥y轴,垂足为C.
(1)如图1,求点A的坐标.
(2)点D在线段AC上,点E是直线AB上一动点,连接DE、以DE为边作正三角形DEF(点D,E,F按逆时针排列)
①如图2,当点E与点A重合时,连接OD,BF.若BF=2,求点D的坐标.
②若CD=2,点P是直线DF与直线OA的交点,当OP=时,直接写出点E的坐标.
10.如图,在Rt△ABC中,∠ACB=90°.
(1)请用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法和证明);
(2)在(1)作出的图形中,若∠A=30°,BC= ,则点D到AB的距离等于 .
答案解析部分
1.【答案】C
【解析】【解答】解:∵∠ACB=90°,
则AB为斜边,
∴BC= = ,
故答案为:C.
【分析】根据∠ACB=90°得出AB为斜边,再用勾股定理求解.
2.【答案】D
【解析】【解答】解:∵一个直角三角形的两条直角边长分别是6和8,
∴斜边长为:,
故答案为:D.
【分析】根据题意利用勾股定理计算求解即可。
3.【答案】D
【解析】【解答】解:设斜边上的高为h,
由勾股定理得,三角形的斜边长= ,
则 ,
解得,h=2.4,
故答案为:D.
【分析】根据勾股定理求出斜边的边长,在应用等积法即可求得斜边上的高.
4.【答案】
【解析】【解答】解: , , ,
,
,
,
故答案为: .
【分析】利用直角三角形30度角的性质求出b,再利用勾股定理求出a即可.
5.【答案】30
【解析】【解答】由勾股定理得: =10,
∴阴影小长方形的面积S=3×10=30;
故答案是:30.
【分析】由勾股定理求出小长方形的长,再由长方形的面积公式进行计算.
6.【答案】24
【解析】【解答】设三边长分别为:
根据勾股定理可得:
解得: (不符合题意,舍去)
三角形的三边长分别为:
则周长为:
故答案为:24.
【分析】由题意可设三边长分别为:2n-2,2n,2n+2,根据勾股定理可得关于n的方程,解方程可求得三角形的各边长,再根据三角形的周长=三角形三边之和可求解.
7.【答案】解:设米,
则,,
,
,
即:,
,
,
.
答:旗杆的高度为米.
【解析】【分析】利用勾股定理列方程求出 , 再解方程即可。
8.【答案】解:如图所示,连接AC,
∵∠D=90°,
∴AC2=AD2+CD2,
∴AC=10,
又∵AC2+BC2=676,AB2=262=676,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ABC-S△ACD=
【解析】【分析】根据题意,连接AC,根据题意可得出△ABC为直角三角形,利用两个三角形的面积差,可得出菜地面积。
9.【答案】(1)解:∵点B的坐标为(0,4),△OAB是正三角形,且AC⊥y轴,
∴AC是边OB的中线,
∴C(0,2),
在Rt△ACO中,AO=4,CO=2,
由勾股定理可得,AC=6,
∴A(6,2).
(2)解:①AF=AD,AB=AO,
∵△OAB和△DEF是正三角形,
∴∠CAF=∠OAB=60°,
∵∠BAF=∠CAF-60°,∠OAD=∠OB-60°,
∴∠BAF=∠OAD,
在△BAF和△OAD中,
,
∴△BAF≌△OAD(SAS),
∴OD=BF=2,
∵OC=2,
∴CD=4,
∴D(4,2);
②(,)或(,).
【解析】【解答】解:(2)②当点P在x轴下方时,如图,连接OD,过点E作AC的垂线,交CA的延长线于点G,
则∠GAE=30°,
在Rt△ODC中,∠OCD=90°,CD=2,OC=2,
∴OD=4,∠COD=30°,
∴AD=OD=4,
∵∠AOC=60°,
∴∠AOD=30°
∴∠DOP=150°,
∵∠GAE=∠BAC=30°,
∴∠DOP=∠DAE=150°,
∵∠CDO=∠EDF=60°,
∴∠ODA=∠EDP=120°,
∴∠ODA-∠DOE=∠EDP-∠DOE
∴∠PDO=∠EDA,
∴△PDO≌△EDA(ASA),
∴OP=AE,
∴GE,AG,
∵A(6,2),
∴E(,);
当点P在x轴上方时,如图,连接OD,过点E作EG⊥AC于点G,
同上可知,△P′DO≌△EDA(ASA),
∴OP=AE,
∴GE,AG,
∵A(6,2),
∴E(,);
综上可知,点E的坐标为(,)或(,).
【分析】(1)根据等边三角形的性质结合点B的坐标可得C(0,2),在Rt△ACO中,根据勾股定理可得AC的值,进而可得点A的坐标;
(2)①由正三角形的性质可得∠CAF=∠OAB=60°,结合角的和差关系可得∠BAF=∠OAD,证明△BAF≌△OAD,得到OD=BF=2,利用勾股定理可得CD,进而可得点D的坐标;
②当点P在x轴下方时,连接OD,过点E作AC的垂线,交CA的延长线于点G,则∠GAE=30°,易得OD=4,∠COD=30°,AD=OD=4,证明△PDO≌△EDA,得到OP=AE,然后求出GE、AG,结合点A的坐标就可求出点E的坐标;当点P在x轴上方时,连接OD,过点E作EG⊥AC于点G,
同上可知△P′DO≌△EDA,OP=AE,同理可得点E的坐标.
10.【答案】(1)解:如图所示,BD即为所求;
(2)1
【解析】【解答】解:(1)如图所示,BD即为所求;
;(2)设DC=x,
过点D作DE⊥AB于E,
则∠DEB=∠C=90°,
∵BD平分∠ABC,
∴DE=DC=x,
∵∠A=30°,BC= ,
∴AD=2DE=2x,AB=2BC=2 ,
由BC2+AC2=AB2得( )2+(3x)2=(2 )2,
解得:x=1(负值舍去),
∴DE=1,即点D到AB的距离等于1,
故答案为:1.
【分析】(1)根据角平分线的作法和步骤作图即可;
(2)设DC=x,过点D作DE⊥AB于E,根据角平线的性质可知DE=DC=x,根据直角三角形中30°所对的直角边等于斜边的一半,可知AD=2DE=2x,AB=2BC=2,由勾股定理易知BC2+AC2=AB2,即()2+(3x)2=(2)2,从而得解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
