四年级下册数学北师大版2.4 探索与发现:三角形边的关系课件(共26张PPT)
文档属性
| 名称 | 四年级下册数学北师大版2.4 探索与发现:三角形边的关系课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 10:34:57 | ||
图片预览




文档简介
(共26张PPT)
北师版四年级数学下册
认识三角形
和四边形
探索与发现:三角形边的关系
汇报人:XXX 时间:XXXXX
经历三角形三边关系的探索过程,知道三角形任意两条边的和大于第三边。
结合操作活动,提高观察、操作、推理能力。
经历活动中问题提出与解决的过程,渗透探索精神的培养。
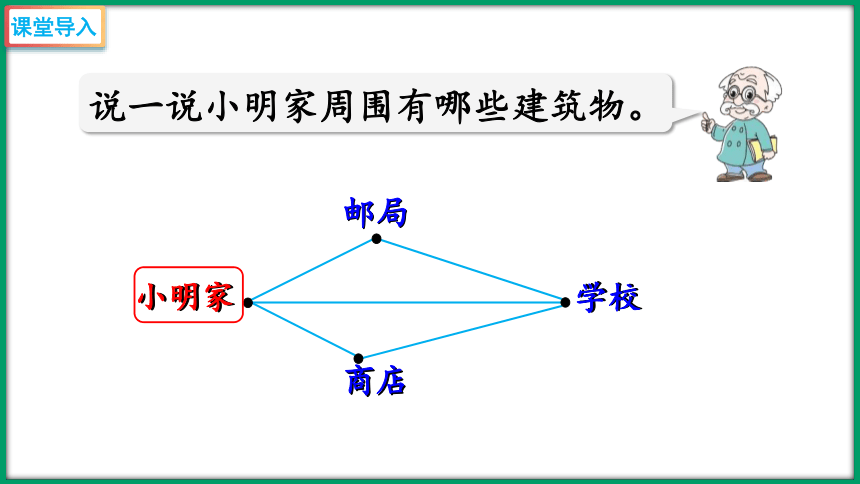
小明家
邮局
学校
商店
邮局
学校
商店
说一说小明家周围有哪些建筑物。
小明家
小明家
邮局
学校
商店
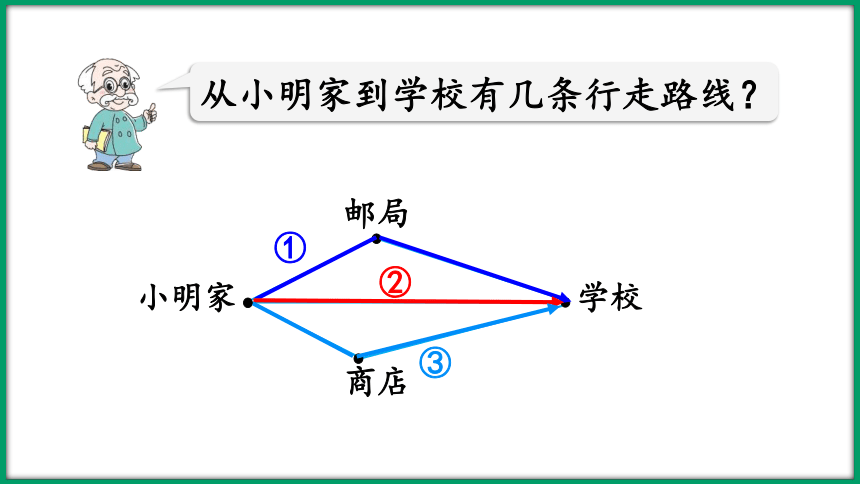
从小明家到学校有几条行走路线?
①
②
③
小明家
邮局
学校
商店
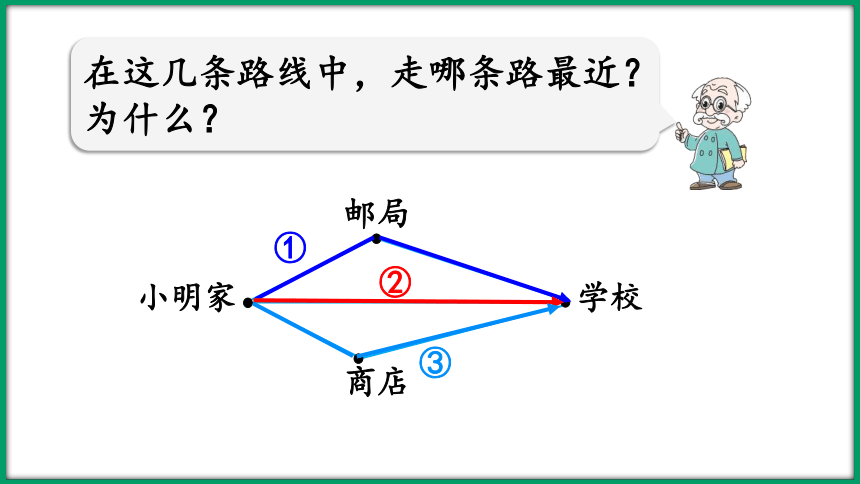
在这几条路线中,走哪条路最近?为什么?
①
②
③
用小棒摆三角形,下面哪组能摆成?哪组摆不成?(单位:厘米)
3
5
6
3
4
6
3
3
6
3
2
6
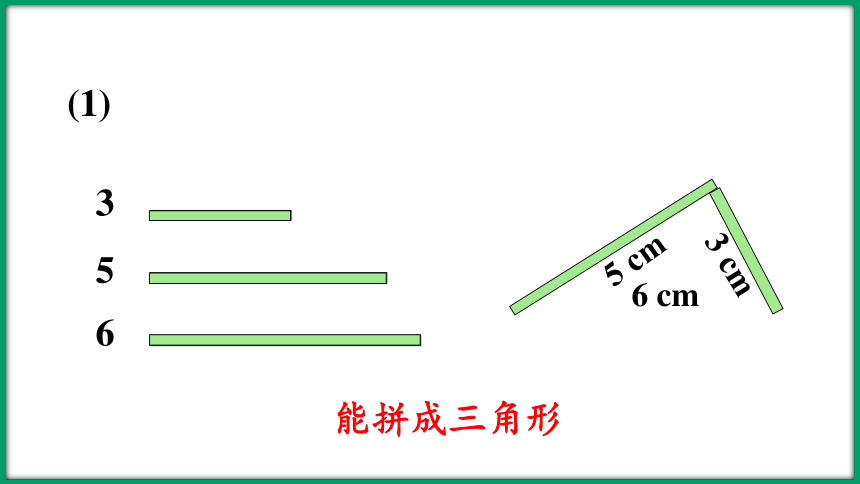
(1)
(3)
(2)
(4)
(1)
3
5
6
3 cm
5 cm
6 cm
能拼成三角形
(2)
4 cm
3 cm
3
4
6
6 cm
能拼成三角形
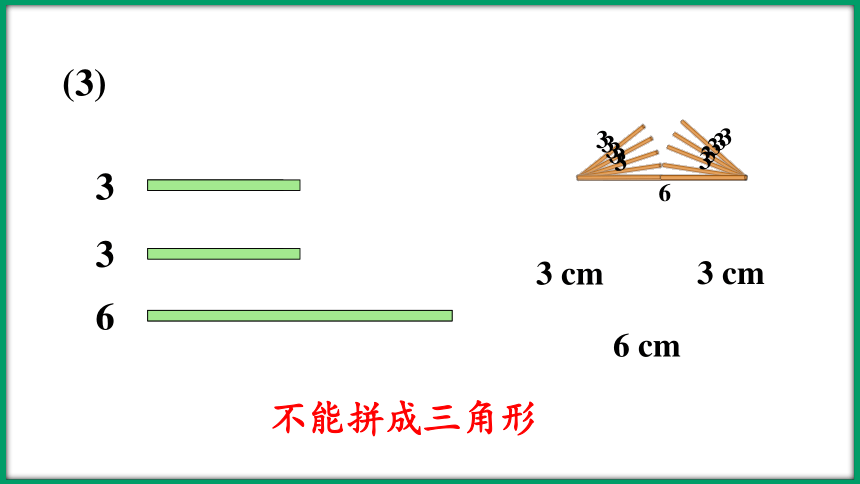
(3)
3
3
6
不能拼成三角形
3 cm
3 cm
6 cm
3
6
3
3
3
3
3
3
3
3
3
(4)
3
2
6
不能拼成三角形
3 cm
2 cm
6 cm
2
6
3
2
2
2
2
3
3
3
3
发现:只有当较短的两根小棒的长度和大于最长
的那根小棒的长度时,才能摆成三角形。
3
5
6
3
4
6
5+3>6
4+3>6
想一想,怎样的3根小棒能摆成一个三角形
发现:当较短的两根小棒的长度和小于或等于最
长的那根小棒的长度时,不能摆成三角形。
3
3
6
2
3
6
3+3=6
3+2<6
想一想,怎样的3根小棒能摆成一个三角形
算一算,比一比,能摆成三角形的3根小棒长度
之间有什么关系 (单位:厘米)
3+6>5
3+5>6
5+6>3
算一算,比一比,能摆成三角形的3根小棒长度
之间有什么关系 (单位:厘米)
3+4>6
3+6>4
4+6>3
发现:能摆成三角形的3根小棒,任意两根小棒的
长度和都大于第三根小棒的长度。
明确三角形三边的关系
1.三角形任意两边之和大于第三边。
2.三角形任意两边之差小于第三边。
设三角形三边分别为 a b c
有a+b>c a-b1.选一选。
(1) 下面( A )组中的三根小棒不能围成三角形。(单位:cm)
A
B
C
解析:根据“三角形任意两边之和大于第三边”进行判断,选项A中因为
4+5<10,较短的两条边的和比第三条边小,所以选项A的小棒不能围成三角形;选项B和C中,因为3+4>6,5+7>11,所以选项B和C能围成三角形。
A
课堂练习
(2) 一个三角形,两边的长分别是8 cm和13 cm,第三条边
的长不可能是( C )。
A. 6 cm B. 8 cm C. 21 cm
C
解析:根据三角形三条边的关系,三角形任意两边之和大于第三
边,可知8 cm+13 cm>第三条边的长度,即第三条边的长度一定小于21 cm。而第三条边也可以是较短的,则有第三条边的长度+8 cm>13 cm,即第三条边的长度要大于5 cm,所以第三条边的长度在5 cm与21 cm之间。故选C。
(3) 用25根同样长的火柴棒摆成一个三角形,最长的边最多
可以由( C )根火柴棒组成。
A. 10 B. 11 C. 12
解析:根据三角形任意两边之和大于第三边,可知要想出现最长边,一定要有最短边,最短为1根,还剩24根,剩下两边只能是12根、12根,所以三条边中最长的边最多可以由12根火柴棒组成。故选C。
C
(4) 一个三角形,其中两条边的长度分别是3 cm、8 cm,第
三条边的长度也是整厘米数。围成这个三角形,最少需
要( A )cm长的绳子。
A. 17 B. 18 C. 19
A
解析:由三角形任意两边之和大于第三边,可知3 cm+8 cm>第三条边的长度,即第三条边的长度一定小于11 cm。而第三条边也可以是较短的,则有第三条边的长度+3 cm>8 cm,即第三条边的长度要大于5 cm,所以第三条边的长度在5 cm与11 cm之间,且为整厘米数。因此第三条边长最短是6 cm,则三角形的周长是3+8+6=17(cm),所以选A。
2 从下面4根小棒中选出3根围成一个三角形,你准备怎样
选择?
选择长度是3厘米、4厘米和5厘米的小棒或选择长度是 5厘米、8厘米和4厘米的小棒。
解析:根据三角形任意两边之和大于第三边解答即可。
3.莱莱的姐姐身高1.72米,体重52千克,腿长约95厘米。莱莱
说他姐姐走一步能迈2米,对于这种说法,你相信吗? 请从数
学角度解释一下。
95+95=190(厘米)
190厘米=1.9米 1.9<2
答:我不相信,两条腿与姐姐走一步的长度可以看成一
个三角形,那么姐姐走一步的长度一定小于1.9米,而2
米大于1.9米,所以姐姐走一步不能迈2米。
4.“又是一年三月三,风筝飞满天”,放风筝是民间传统游戏之一。聪聪做了一个等腰三角形形状的风筝。如果等腰三角形的两条边长分别是46 cm和21 cm,这个等腰三角形的周长是多少厘米?
46+46+21=113(cm)
答:这个等腰三角形的周长是113 cm。
解析:本题考查的是周长的意义和等腰三角形的特征。由等腰三角
形的两条边相等,21 cm长的边不能作为腰,可得这个等腰三角形
的两腰长是46 cm,底边长是21 cm,所以等腰三角形的周长是46+
46+21=113(cm)。
5.一块等腰三角形的土地,周长是180 m,其中一
条边的长是50 m,另外两条边的长分别是多少米?
解析:假设腰长是50 m,则第三条边即底边长=三角形的周长-腰长×2,假设50 m是底边长,则腰长=(三角形的周长-底边长)÷2,据此解答。
如果50 m是腰长,底边长:180-50×2=80(m)
如果50 m是底边长,腰长:(180-50)÷2=65(m)
答:另外两条边的长分别是50 m、80 m或65 m、65 m。
1.一个三角形的两条边的长度分别是3厘米和9厘米,另一个三角形的两条边的长度分别是2厘米和6厘米。已知这两个三角形的第三条边一样长,而且长度是整厘米数,它们的第三条边的长度是多少?
它们的第三条边的长度是7厘米。
思维拓展
解析:3+9=12(厘米),2+6=8(厘米),这两个三角形的第三条边
一样长,根据“三角形任意两边之和大于第三边”,可知第三条边
的长度小于8厘米,可能是7,6,5,4,3,2,1(单位:厘米)。但
由于有一个三角形的两条边的长度分别是3厘米和9厘米,如果第三
条边的长度是6厘米,3+6=9(厘米),不能组成三角形,所以小于
或等于6厘米的都不行,答案只有7厘米。
同学们,这节课你们学会了哪些知识?
1. 三角形任意两边之和大于第三边。
2. 判断三条线段是否能围成三角形,只要把较短的两条线段的长度相加的和与第三条线段比较即可。若较短两边的长度和大于第三条线段,就一定能围成三角形;否则,就不能围成三角形。
北师版四年级数学下册
认识三角形
和四边形
探索与发现:三角形边的关系
汇报人:XXX 时间:XXXXX
经历三角形三边关系的探索过程,知道三角形任意两条边的和大于第三边。
结合操作活动,提高观察、操作、推理能力。
经历活动中问题提出与解决的过程,渗透探索精神的培养。
小明家
邮局
学校
商店
邮局
学校
商店
说一说小明家周围有哪些建筑物。
小明家
小明家
邮局
学校
商店
从小明家到学校有几条行走路线?
①
②
③
小明家
邮局
学校
商店
在这几条路线中,走哪条路最近?为什么?
①
②
③
用小棒摆三角形,下面哪组能摆成?哪组摆不成?(单位:厘米)
3
5
6
3
4
6
3
3
6
3
2
6
(1)
(3)
(2)
(4)
(1)
3
5
6
3 cm
5 cm
6 cm
能拼成三角形
(2)
4 cm
3 cm
3
4
6
6 cm
能拼成三角形
(3)
3
3
6
不能拼成三角形
3 cm
3 cm
6 cm
3
6
3
3
3
3
3
3
3
3
3
(4)
3
2
6
不能拼成三角形
3 cm
2 cm
6 cm
2
6
3
2
2
2
2
3
3
3
3
发现:只有当较短的两根小棒的长度和大于最长
的那根小棒的长度时,才能摆成三角形。
3
5
6
3
4
6
5+3>6
4+3>6
想一想,怎样的3根小棒能摆成一个三角形
发现:当较短的两根小棒的长度和小于或等于最
长的那根小棒的长度时,不能摆成三角形。
3
3
6
2
3
6
3+3=6
3+2<6
想一想,怎样的3根小棒能摆成一个三角形
算一算,比一比,能摆成三角形的3根小棒长度
之间有什么关系 (单位:厘米)
3+6>5
3+5>6
5+6>3
算一算,比一比,能摆成三角形的3根小棒长度
之间有什么关系 (单位:厘米)
3+4>6
3+6>4
4+6>3
发现:能摆成三角形的3根小棒,任意两根小棒的
长度和都大于第三根小棒的长度。
明确三角形三边的关系
1.三角形任意两边之和大于第三边。
2.三角形任意两边之差小于第三边。
设三角形三边分别为 a b c
有a+b>c a-b
(1) 下面( A )组中的三根小棒不能围成三角形。(单位:cm)
A
B
C
解析:根据“三角形任意两边之和大于第三边”进行判断,选项A中因为
4+5<10,较短的两条边的和比第三条边小,所以选项A的小棒不能围成三角形;选项B和C中,因为3+4>6,5+7>11,所以选项B和C能围成三角形。
A
课堂练习
(2) 一个三角形,两边的长分别是8 cm和13 cm,第三条边
的长不可能是( C )。
A. 6 cm B. 8 cm C. 21 cm
C
解析:根据三角形三条边的关系,三角形任意两边之和大于第三
边,可知8 cm+13 cm>第三条边的长度,即第三条边的长度一定小于21 cm。而第三条边也可以是较短的,则有第三条边的长度+8 cm>13 cm,即第三条边的长度要大于5 cm,所以第三条边的长度在5 cm与21 cm之间。故选C。
(3) 用25根同样长的火柴棒摆成一个三角形,最长的边最多
可以由( C )根火柴棒组成。
A. 10 B. 11 C. 12
解析:根据三角形任意两边之和大于第三边,可知要想出现最长边,一定要有最短边,最短为1根,还剩24根,剩下两边只能是12根、12根,所以三条边中最长的边最多可以由12根火柴棒组成。故选C。
C
(4) 一个三角形,其中两条边的长度分别是3 cm、8 cm,第
三条边的长度也是整厘米数。围成这个三角形,最少需
要( A )cm长的绳子。
A. 17 B. 18 C. 19
A
解析:由三角形任意两边之和大于第三边,可知3 cm+8 cm>第三条边的长度,即第三条边的长度一定小于11 cm。而第三条边也可以是较短的,则有第三条边的长度+3 cm>8 cm,即第三条边的长度要大于5 cm,所以第三条边的长度在5 cm与11 cm之间,且为整厘米数。因此第三条边长最短是6 cm,则三角形的周长是3+8+6=17(cm),所以选A。
2 从下面4根小棒中选出3根围成一个三角形,你准备怎样
选择?
选择长度是3厘米、4厘米和5厘米的小棒或选择长度是 5厘米、8厘米和4厘米的小棒。
解析:根据三角形任意两边之和大于第三边解答即可。
3.莱莱的姐姐身高1.72米,体重52千克,腿长约95厘米。莱莱
说他姐姐走一步能迈2米,对于这种说法,你相信吗? 请从数
学角度解释一下。
95+95=190(厘米)
190厘米=1.9米 1.9<2
答:我不相信,两条腿与姐姐走一步的长度可以看成一
个三角形,那么姐姐走一步的长度一定小于1.9米,而2
米大于1.9米,所以姐姐走一步不能迈2米。
4.“又是一年三月三,风筝飞满天”,放风筝是民间传统游戏之一。聪聪做了一个等腰三角形形状的风筝。如果等腰三角形的两条边长分别是46 cm和21 cm,这个等腰三角形的周长是多少厘米?
46+46+21=113(cm)
答:这个等腰三角形的周长是113 cm。
解析:本题考查的是周长的意义和等腰三角形的特征。由等腰三角
形的两条边相等,21 cm长的边不能作为腰,可得这个等腰三角形
的两腰长是46 cm,底边长是21 cm,所以等腰三角形的周长是46+
46+21=113(cm)。
5.一块等腰三角形的土地,周长是180 m,其中一
条边的长是50 m,另外两条边的长分别是多少米?
解析:假设腰长是50 m,则第三条边即底边长=三角形的周长-腰长×2,假设50 m是底边长,则腰长=(三角形的周长-底边长)÷2,据此解答。
如果50 m是腰长,底边长:180-50×2=80(m)
如果50 m是底边长,腰长:(180-50)÷2=65(m)
答:另外两条边的长分别是50 m、80 m或65 m、65 m。
1.一个三角形的两条边的长度分别是3厘米和9厘米,另一个三角形的两条边的长度分别是2厘米和6厘米。已知这两个三角形的第三条边一样长,而且长度是整厘米数,它们的第三条边的长度是多少?
它们的第三条边的长度是7厘米。
思维拓展
解析:3+9=12(厘米),2+6=8(厘米),这两个三角形的第三条边
一样长,根据“三角形任意两边之和大于第三边”,可知第三条边
的长度小于8厘米,可能是7,6,5,4,3,2,1(单位:厘米)。但
由于有一个三角形的两条边的长度分别是3厘米和9厘米,如果第三
条边的长度是6厘米,3+6=9(厘米),不能组成三角形,所以小于
或等于6厘米的都不行,答案只有7厘米。
同学们,这节课你们学会了哪些知识?
1. 三角形任意两边之和大于第三边。
2. 判断三条线段是否能围成三角形,只要把较短的两条线段的长度相加的和与第三条线段比较即可。若较短两边的长度和大于第三条线段,就一定能围成三角形;否则,就不能围成三角形。
