四年级下册数学北师大版2.3 探索与发现:三角形内角和课件(共34张PPT)
文档属性
| 名称 | 四年级下册数学北师大版2.3 探索与发现:三角形内角和课件(共34张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 10:36:03 | ||
图片预览




文档简介
(共34张PPT)
北师版四年级数学下册
认识三角形
和四边形
探索与发现:三角形内角和
汇报人:XXX 时间:XXXXX
1.通过量、剪、拼、折等直观操作活动,探索并发现三
角形内角和等于180°,发展动手操作、观察比较的
能力。
2.能运用三角形内角和的性质解决一些简单的实际问题。
3.在亲历探索发现的过程中,体验数学思考与探究的乐
趣,培养学习数学的兴趣。
什么是平角?平角有多少度?
1800
课堂导入
正方形和长方形的内角和是多少度?
900
900
900
900
900
900
900
900
长方形内角和3600,三角形呢?
小组活动:每人准备一个三角形,量一量,填一填。
小组活动记录表
第 组
小组成员姓名 三角形的形状 每个内角的度数 三个内角的和
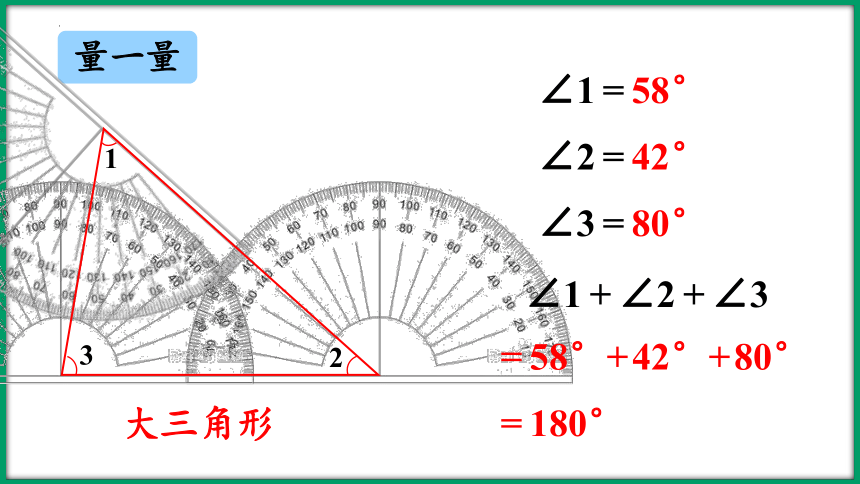
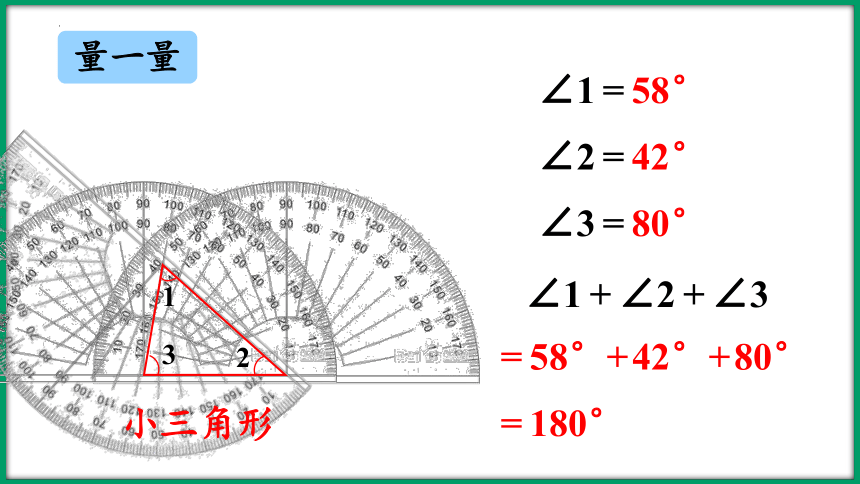
量一量
大三角形
1
3
2
∠1=58°
∠2=42°
∠3=80°
∠1+∠2+∠3
=58°+42°+80°
=180°
量一量
小三角形
1
3
2
∠1=58°
∠2=42°
∠3=80°
∠1+∠2+∠3
=58°+42°+80°
=180°
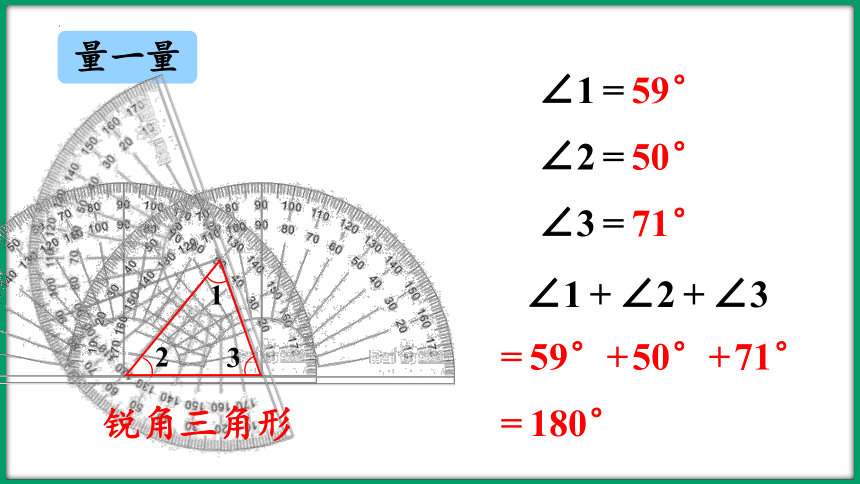
量一量
锐角三角形
1
2
3
∠1=59°
∠2=50°
∠3=71°
∠1+∠2+∠3
=59°+50°+71°
=180°
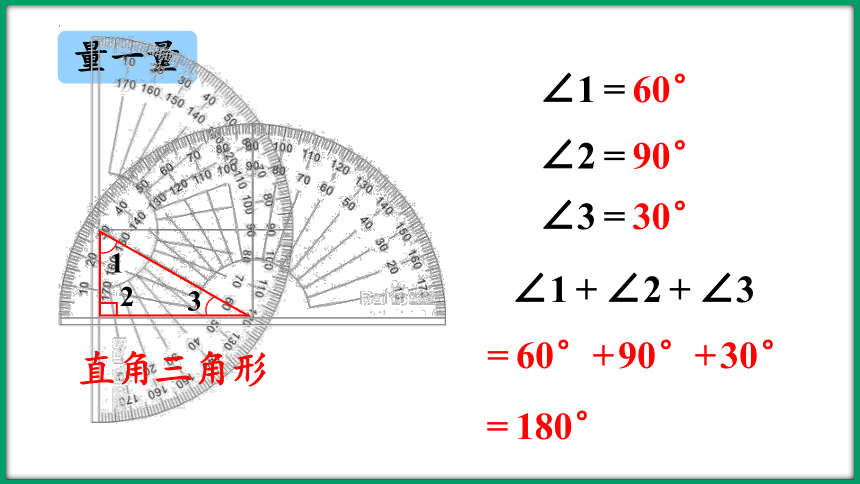
量一量
直角三角形
∠1=60°
∠2=90°
∠3=30°
∠1+∠2+∠3
=60°+90°+30°
=180°
1
2
3
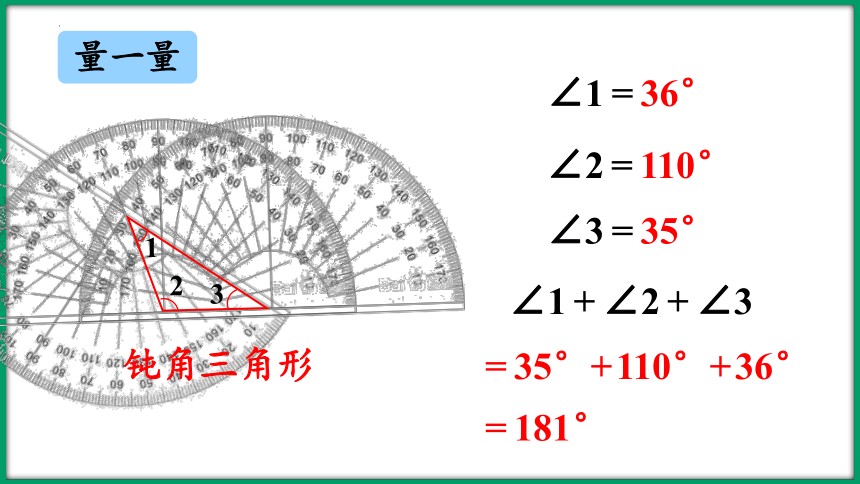
钝角三角形
∠1=36°
∠2=110°
∠3=35°
∠1+∠2+∠3
=35°+110°+36°
=181°
1
2
3
量一量
三角形的形状 每个内角的度数 三个内角的和
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
59°
50°
71°
180°
90°
30°
60°
180°
36°
110°
35°
181°
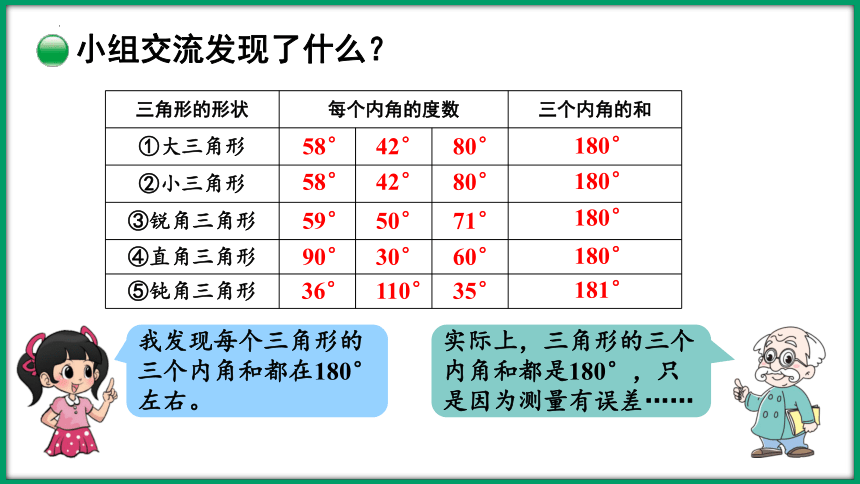
小组交流发现了什么?
我发现每个三角形的三个内角和都在180°左右。
实际上,三角形的三个内角和都是180°,只是因为测量有误差……
58°
42°
80°
180°
58°
42°
80°
180°
方法一:把三角形的三个角撕下来,拼在一起,如图。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
方法二:将三角形折成一个长方形,并使三个内角的顶
点折到同一点,如图所示。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
综上可以得出结论:三角形的内角和等于180°。也就是说,三角形的内角和与三角形的大小、形状无关,三角形的内角和永远是180°。
有什么方法能验证你们的想法?说一说,做一做。
60°
40°
80°
180 60 40=80°
锐角三角形
猜一猜,可能是什么三角形?
你还能猜出是什么三角形吗?
三角形的内角和为180°
另外两个内角和为:180° 60°=120°
①另外两个角可能是:50°和70°。
②另外两个角可能是:90°和30°。
③另外两个角可能是:110°和10°。
60°
60°
60°
锐角三角形
钝角三角形
等边三角形
直角三角形
60°
你还能猜出是什么三角形吗?
1.想一想,填一填。
(1)云云在验证三角形的内角和是( 180 )°时,把一个
三角形的三个角剪下来进行了拼接(如图)。已知这个三角形
中∠1=35°,∠3=70°,那么∠2=( 75° )。
180
75°
课堂练
(2)在一个三角形中,最大的角是78°,这个三角形是
( 锐角 )三角形。
(3)一个三角形的两个内角分别是95°和27°,则另一个内
角的度数是( 58° )。
锐角
58°
(4)有一个角是60°的等腰三角形一定是( 等边 )三角
形,它的三个内角的度数都是( 60° )。
等边
60°
2.选一选。
(1) 下列选项中,不能作为一个三角形的三个角的度数的是
( B )。
A.107°,52°,21° B.90°,43°,57°
C.80°,20°,80°
B
解析:将三个度数相加,度数和等于180°的就可以作为三角形三个内角的度数,如果不等于180°,就不能作为三角形三个内角的度数。
(2) 等腰三角形中有一个内角是40°,另外两个内角( C )。
A.都是70° B.是40°和100°
C.A、B都对
C
解析:等腰三角形的两个底角相等。已知等腰三角形的一个内角是40°,但并不知是顶角还是底角,所以要分两种情况解答。若40°是底角,则顶角是180°-40°×2=100°;若40°是顶角,则底角是(180°-40°)÷2=70°,故选C。
3.量一量,猜一猜,可能是什么三角形?
( 直角三角形 ) ( 钝角三角形 )
( 锐角三角形或直角三角
形或钝角三角形 )
直角三角形
钝角三角形
锐角三角形或直角三角
形或钝角三角形
( 锐角三角形 )
锐角三角形
4.求下列三角形未知角的度数。
(1) 180°-37°-54°=89°
(2) 180°-81°-19°=80°
解析:根据三角形内角和是180°,已知两个角的度数,用180°连续减去这两个已知角的度数即可求出未知角的度数。
180°-37°-54°=89°
180°-81°-19°=80°
5.如图,它是由一个等边三角形和一个等腰三角形
拼成的,求图中∠1的度数。
180°-60°=120°
∠1=(180°-120°)÷2=30°
答:图中∠1的度数是30°。
解析:易知等边三角形的三个内角都是60°,由题图可得等边三角形的一个角与等腰三角形的顶角合起来是180°,则等腰三角形的顶角为
180°-60°=120°,又因为在等腰三角形中,两底角相等,
所以∠1=(180°-120°)÷2=30°。
6.解决问题。
(1)在三角形ABC中,∠A=65°,∠B比∠A小15°,∠C是多
少度?
∠B=65°-15°=50°
∠C=180°-65°-50°=65°
答:∠C是65°。
(2)在三角形ABC中,∠B的度数是30°,∠A的度数是
∠B的3倍,求∠C的度数。
∠A=30°×3=90°
∠C=180°-90°-30°=60°
答:∠C的度数是60°。
7.一个等腰三角形顶角的度数是底角的4倍,它的顶角是多少度?
底角度数:180°÷(1+1+4)=30°
顶角度数:30°×4=120°
答:它的顶角是120°。
解析:根据题意,将底角的度数看作1份,顶角的度数就是4份,因为等腰三角形两个底角相等,所以三个内角份数和为(4+1+1)份,6份对应三角形内角和是180°,则一份对应度数为180°÷6,即一个底角的度数,再乘4即可求出顶角的度数。
8.有一张直角三角形纸片,剪去直角后变成一个四边形,
求∠1与∠2的和。
∠3+∠4=180°-90°=90°
∠1+∠2=360°-(∠3+∠4)=360°-90°=270°
答:∠1与∠2的和是270°。
解析:先根据三角形的内角和求出∠3+∠4的度数;再根据四边形的内角和是360°求出∠1与∠2的度数和。
1.如图,两个重叠的等腰三角形,并且∠1=∠2,∠3=∠4,∠5=112°,求∠6的度数。
因为∠2=∠4,∠5=112°,∠2+∠4+∠5=180°,
所以∠2=∠4=(180°-112°)÷2=34°。
因为∠1=∠2,∠3=∠4,
∠1+∠2+∠3+∠4+
∠6=180°,所以∠6=180°-34°×4=44°。
答:∠6的度数是44°。
思维拓展
因为∠2=∠4,∠5=112°,∠2+∠4+∠5=180°,
所以∠2=∠4=(180°-112°)÷2=34°。
因为∠1=∠2,∠3=∠4,
∠1+∠2+∠3+∠4+
∠6=180°,所以∠6=180°-34°×4=44°。
答:∠6的度数是44°。
2.下图中,∠1=100°,∠2=∠3,且∠2+∠3=∠4,求
∠5的度数。
∠2+∠3+∠4=180°-100°=80°
∠4=∠2+∠3=80°÷2=40°
∠3=40°÷2=20°
∠5=180°-∠3-∠4=120°
答:∠5的度数是120°。
解析:根据三角形的内角和等于180°可知,∠1+∠2+∠3+∠4
=180°,∠3+∠4+∠5=180°。因为∠1=100°,∠2=∠3且
∠2+∠3=∠4,所以∠4=∠2+∠3=(180°-100°)÷2=
40°,∠3=40°÷2=20°,∠5=180°-∠3-∠4=120°。
同学们,这节课你们学会了哪些知识?
1.三角形内角和等于180°,与三角形的大小、形状无关。
2.根据三角形内角和等于180°,当已知三角形中两个内角的度数时,可以求出第三个内角的度数,并可以由此判断三角形的形状。
北师版四年级数学下册
认识三角形
和四边形
探索与发现:三角形内角和
汇报人:XXX 时间:XXXXX
1.通过量、剪、拼、折等直观操作活动,探索并发现三
角形内角和等于180°,发展动手操作、观察比较的
能力。
2.能运用三角形内角和的性质解决一些简单的实际问题。
3.在亲历探索发现的过程中,体验数学思考与探究的乐
趣,培养学习数学的兴趣。
什么是平角?平角有多少度?
1800
课堂导入
正方形和长方形的内角和是多少度?
900
900
900
900
900
900
900
900
长方形内角和3600,三角形呢?
小组活动:每人准备一个三角形,量一量,填一填。
小组活动记录表
第 组
小组成员姓名 三角形的形状 每个内角的度数 三个内角的和
量一量
大三角形
1
3
2
∠1=58°
∠2=42°
∠3=80°
∠1+∠2+∠3
=58°+42°+80°
=180°
量一量
小三角形
1
3
2
∠1=58°
∠2=42°
∠3=80°
∠1+∠2+∠3
=58°+42°+80°
=180°
量一量
锐角三角形
1
2
3
∠1=59°
∠2=50°
∠3=71°
∠1+∠2+∠3
=59°+50°+71°
=180°
量一量
直角三角形
∠1=60°
∠2=90°
∠3=30°
∠1+∠2+∠3
=60°+90°+30°
=180°
1
2
3
钝角三角形
∠1=36°
∠2=110°
∠3=35°
∠1+∠2+∠3
=35°+110°+36°
=181°
1
2
3
量一量
三角形的形状 每个内角的度数 三个内角的和
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
59°
50°
71°
180°
90°
30°
60°
180°
36°
110°
35°
181°
小组交流发现了什么?
我发现每个三角形的三个内角和都在180°左右。
实际上,三角形的三个内角和都是180°,只是因为测量有误差……
58°
42°
80°
180°
58°
42°
80°
180°
方法一:把三角形的三个角撕下来,拼在一起,如图。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
方法二:将三角形折成一个长方形,并使三个内角的顶
点折到同一点,如图所示。
∠1,∠2,∠3正好拼成一个平角,说明三角形的内角和是180°。
有什么方法能验证你们的想法?说一说,做一做。
综上可以得出结论:三角形的内角和等于180°。也就是说,三角形的内角和与三角形的大小、形状无关,三角形的内角和永远是180°。
有什么方法能验证你们的想法?说一说,做一做。
60°
40°
80°
180 60 40=80°
锐角三角形
猜一猜,可能是什么三角形?
你还能猜出是什么三角形吗?
三角形的内角和为180°
另外两个内角和为:180° 60°=120°
①另外两个角可能是:50°和70°。
②另外两个角可能是:90°和30°。
③另外两个角可能是:110°和10°。
60°
60°
60°
锐角三角形
钝角三角形
等边三角形
直角三角形
60°
你还能猜出是什么三角形吗?
1.想一想,填一填。
(1)云云在验证三角形的内角和是( 180 )°时,把一个
三角形的三个角剪下来进行了拼接(如图)。已知这个三角形
中∠1=35°,∠3=70°,那么∠2=( 75° )。
180
75°
课堂练
(2)在一个三角形中,最大的角是78°,这个三角形是
( 锐角 )三角形。
(3)一个三角形的两个内角分别是95°和27°,则另一个内
角的度数是( 58° )。
锐角
58°
(4)有一个角是60°的等腰三角形一定是( 等边 )三角
形,它的三个内角的度数都是( 60° )。
等边
60°
2.选一选。
(1) 下列选项中,不能作为一个三角形的三个角的度数的是
( B )。
A.107°,52°,21° B.90°,43°,57°
C.80°,20°,80°
B
解析:将三个度数相加,度数和等于180°的就可以作为三角形三个内角的度数,如果不等于180°,就不能作为三角形三个内角的度数。
(2) 等腰三角形中有一个内角是40°,另外两个内角( C )。
A.都是70° B.是40°和100°
C.A、B都对
C
解析:等腰三角形的两个底角相等。已知等腰三角形的一个内角是40°,但并不知是顶角还是底角,所以要分两种情况解答。若40°是底角,则顶角是180°-40°×2=100°;若40°是顶角,则底角是(180°-40°)÷2=70°,故选C。
3.量一量,猜一猜,可能是什么三角形?
( 直角三角形 ) ( 钝角三角形 )
( 锐角三角形或直角三角
形或钝角三角形 )
直角三角形
钝角三角形
锐角三角形或直角三角
形或钝角三角形
( 锐角三角形 )
锐角三角形
4.求下列三角形未知角的度数。
(1) 180°-37°-54°=89°
(2) 180°-81°-19°=80°
解析:根据三角形内角和是180°,已知两个角的度数,用180°连续减去这两个已知角的度数即可求出未知角的度数。
180°-37°-54°=89°
180°-81°-19°=80°
5.如图,它是由一个等边三角形和一个等腰三角形
拼成的,求图中∠1的度数。
180°-60°=120°
∠1=(180°-120°)÷2=30°
答:图中∠1的度数是30°。
解析:易知等边三角形的三个内角都是60°,由题图可得等边三角形的一个角与等腰三角形的顶角合起来是180°,则等腰三角形的顶角为
180°-60°=120°,又因为在等腰三角形中,两底角相等,
所以∠1=(180°-120°)÷2=30°。
6.解决问题。
(1)在三角形ABC中,∠A=65°,∠B比∠A小15°,∠C是多
少度?
∠B=65°-15°=50°
∠C=180°-65°-50°=65°
答:∠C是65°。
(2)在三角形ABC中,∠B的度数是30°,∠A的度数是
∠B的3倍,求∠C的度数。
∠A=30°×3=90°
∠C=180°-90°-30°=60°
答:∠C的度数是60°。
7.一个等腰三角形顶角的度数是底角的4倍,它的顶角是多少度?
底角度数:180°÷(1+1+4)=30°
顶角度数:30°×4=120°
答:它的顶角是120°。
解析:根据题意,将底角的度数看作1份,顶角的度数就是4份,因为等腰三角形两个底角相等,所以三个内角份数和为(4+1+1)份,6份对应三角形内角和是180°,则一份对应度数为180°÷6,即一个底角的度数,再乘4即可求出顶角的度数。
8.有一张直角三角形纸片,剪去直角后变成一个四边形,
求∠1与∠2的和。
∠3+∠4=180°-90°=90°
∠1+∠2=360°-(∠3+∠4)=360°-90°=270°
答:∠1与∠2的和是270°。
解析:先根据三角形的内角和求出∠3+∠4的度数;再根据四边形的内角和是360°求出∠1与∠2的度数和。
1.如图,两个重叠的等腰三角形,并且∠1=∠2,∠3=∠4,∠5=112°,求∠6的度数。
因为∠2=∠4,∠5=112°,∠2+∠4+∠5=180°,
所以∠2=∠4=(180°-112°)÷2=34°。
因为∠1=∠2,∠3=∠4,
∠1+∠2+∠3+∠4+
∠6=180°,所以∠6=180°-34°×4=44°。
答:∠6的度数是44°。
思维拓展
因为∠2=∠4,∠5=112°,∠2+∠4+∠5=180°,
所以∠2=∠4=(180°-112°)÷2=34°。
因为∠1=∠2,∠3=∠4,
∠1+∠2+∠3+∠4+
∠6=180°,所以∠6=180°-34°×4=44°。
答:∠6的度数是44°。
2.下图中,∠1=100°,∠2=∠3,且∠2+∠3=∠4,求
∠5的度数。
∠2+∠3+∠4=180°-100°=80°
∠4=∠2+∠3=80°÷2=40°
∠3=40°÷2=20°
∠5=180°-∠3-∠4=120°
答:∠5的度数是120°。
解析:根据三角形的内角和等于180°可知,∠1+∠2+∠3+∠4
=180°,∠3+∠4+∠5=180°。因为∠1=100°,∠2=∠3且
∠2+∠3=∠4,所以∠4=∠2+∠3=(180°-100°)÷2=
40°,∠3=40°÷2=20°,∠5=180°-∠3-∠4=120°。
同学们,这节课你们学会了哪些知识?
1.三角形内角和等于180°,与三角形的大小、形状无关。
2.根据三角形内角和等于180°,当已知三角形中两个内角的度数时,可以求出第三个内角的度数,并可以由此判断三角形的形状。
