新课标人教A版 选修2-2 1.3导数在研究函数中的应用
文档属性
| 名称 | 新课标人教A版 选修2-2 1.3导数在研究函数中的应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 20.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-06 00:00:00 | ||
图片预览






文档简介
课件18张PPT。导数的应用 马艳玲
函数y=f(x)在x。处的导数是y=f(x)所表示的曲线上( x。,f(x。) )点处的切线的斜率
导数的几何意义xyoy=f(x)一、函数的单调性设函数 y=f(x)在某区间可导,若f ′(x)>0,则y=f(x)在该区间上是增函数;
若f ′(x)<0,则y=f(x)在该区间上是减函数.基础训练1、函数f(x)=x3-3x2+1的减区间是( )
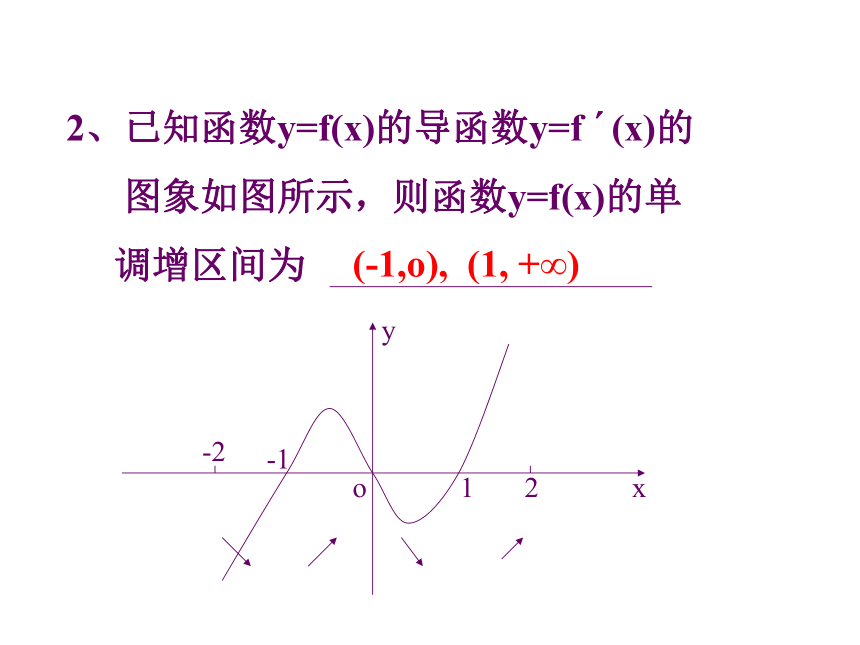
A. (2,+∞) B. (- ∞,2) C. (- ∞,0) D. (0,2)D2、已知函数y=f(x)的导函数y=f ′(x)的
图象如图所示,则函数y=f(x)的单
调增区间为xyo-11-22(-1,o), (1, +∞)二、函数的极值 函数f(x)在点x。附近有定义,
如果对x。附近的所有点都有f(x)如果对x。附近的所有点都有f(x)>f(x。)则f(x。)是函数f(x)的一个极小值;
若函数f(x)在点x。处可导且存在极值,
则f ?(x。)=03、函数f(x)的定义域为R,导函数f ′(x)的图象如图,则函数f(x) ( )
无极大值点,有两个极小值点
有三个极大值点,两个极小值点
有两个极大值点,两个极小值点
有四个极大值点,无极小值点Cxoy三、函数的最值注意严格区分极值和最值的概念.
极值是仅对某一点的附近而言,是在局部范围内讨论问题,而最值是对整个定义域而言,是在整体范围内讨论问题。
4、函数f(x)=x3-3x+1在闭区间[-3,0]上的
最大值、最小值分别是( )
1,-1 B. 1,-17
C. 3,-17 D. 9,-19C?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?例1、已知函数 f(x)=x3+ax2+bx+c 在x=-
与x=1时都取得极值.
⑴ 求a 、b的值与函数f(x)的单调区间;
⑵ 若对x ? [ -1, 2 ],不等式 f(x) 求 c 的取值范围 23例2、已知函数 f(x)=ae - x2
⑴ 若f(x)在R上为增函数,求 a的
取值范围
⑵ 若a=1求证:x>0时,f(x)>1+x12x巩固训练1、函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A. 2 B. 3 C . 4 D. 5 D2函数y=4x2+ 的单调增区间为( )
A.(0,+ ) B.( ,+ ) C.(- ,-1) D.(- ,- )∞∞∞∞2121x1B3 函数y= +x2-3x-4在[0,2]上的最小值是( )
A.- B.- C.-4 D-173310364A3x34、已知函数y=xf?(x)的图象如图所示,下面四个图象中y=f(x)的图象大致是( )xyo12-1-2xxxxyyyy11112222oooo-1-1-1-1-2-2-2-2C+__+
5.函数 f(x)=ax3+bx2+cx 在x=1或x=-1处存在
极值且f(1)=-1,求a、b、c的值,并求其极值。6. 若函数f(x)= x3- ax2+(a-1)x+1在区间
(1,4)内为减函数,在区间(6,+∞)上为增函数,
试求实数a的取值范围.1132思考题:
已知函数f(x)= e
⑴设a>o,讨论y=f(x)的单调性
⑵若对任意x∈(0,1)恒有f(x)>1,求a的取值范围1-x1+x-ax
函数y=f(x)在x。处的导数是y=f(x)所表示的曲线上( x。,f(x。) )点处的切线的斜率
导数的几何意义xyoy=f(x)一、函数的单调性设函数 y=f(x)在某区间可导,若f ′(x)>0,则y=f(x)在该区间上是增函数;
若f ′(x)<0,则y=f(x)在该区间上是减函数.基础训练1、函数f(x)=x3-3x2+1的减区间是( )
A. (2,+∞) B. (- ∞,2) C. (- ∞,0) D. (0,2)D2、已知函数y=f(x)的导函数y=f ′(x)的
图象如图所示,则函数y=f(x)的单
调增区间为xyo-11-22(-1,o), (1, +∞)二、函数的极值 函数f(x)在点x。附近有定义,
如果对x。附近的所有点都有f(x)
若函数f(x)在点x。处可导且存在极值,
则f ?(x。)=03、函数f(x)的定义域为R,导函数f ′(x)的图象如图,则函数f(x) ( )
无极大值点,有两个极小值点
有三个极大值点,两个极小值点
有两个极大值点,两个极小值点
有四个极大值点,无极小值点Cxoy三、函数的最值注意严格区分极值和最值的概念.
极值是仅对某一点的附近而言,是在局部范围内讨论问题,而最值是对整个定义域而言,是在整体范围内讨论问题。
4、函数f(x)=x3-3x+1在闭区间[-3,0]上的
最大值、最小值分别是( )
1,-1 B. 1,-17
C. 3,-17 D. 9,-19C?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?例1、已知函数 f(x)=x3+ax2+bx+c 在x=-
与x=1时都取得极值.
⑴ 求a 、b的值与函数f(x)的单调区间;
⑵ 若对x ? [ -1, 2 ],不等式 f(x)
⑴ 若f(x)在R上为增函数,求 a的
取值范围
⑵ 若a=1求证:x>0时,f(x)>1+x12x巩固训练1、函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于( )
A. 2 B. 3 C . 4 D. 5 D2函数y=4x2+ 的单调增区间为( )
A.(0,+ ) B.( ,+ ) C.(- ,-1) D.(- ,- )∞∞∞∞2121x1B3 函数y= +x2-3x-4在[0,2]上的最小值是( )
A.- B.- C.-4 D-173310364A3x34、已知函数y=xf?(x)的图象如图所示,下面四个图象中y=f(x)的图象大致是( )xyo12-1-2xxxxyyyy11112222oooo-1-1-1-1-2-2-2-2C+__+
5.函数 f(x)=ax3+bx2+cx 在x=1或x=-1处存在
极值且f(1)=-1,求a、b、c的值,并求其极值。6. 若函数f(x)= x3- ax2+(a-1)x+1在区间
(1,4)内为减函数,在区间(6,+∞)上为增函数,
试求实数a的取值范围.1132思考题:
已知函数f(x)= e
⑴设a>o,讨论y=f(x)的单调性
⑵若对任意x∈(0,1)恒有f(x)>1,求a的取值范围1-x1+x-ax
