浙江省杭州市拱墅区锦绣育才教育集团2023-2024学年九年级上学期期末数学试卷(无答案)
文档属性
| 名称 | 浙江省杭州市拱墅区锦绣育才教育集团2023-2024学年九年级上学期期末数学试卷(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 288.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 12:12:00 | ||
图片预览


文档简介
2023-2024学年浙江省杭州市拱墅区锦绣育才教育集团九年级(上)期末数学试卷
一、选择题(本题有10小题,每小题3分,共30分)
1.若△ABC与△DEF的相似比为1:3,则△ABC与△DEF的周长比为( )
A.1:3 B.1:9 C.3:1 D.9:1
2.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.无法确定 B.相切 C.相交 D.相离
3.二次函数y=ax2(a≠0)的图象经过点(2,﹣1),则a的值是( )
A. B. C. D.2
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B.1 C. D.2
5.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A. B. C. D.
6.关于二次函数y=(x﹣2)2﹣3的最大值或最小值,下列叙述正确的是( )
A.当x=2 时,y有最大值﹣3 B.当x=﹣2 时,y有最大值﹣3
C.当x=2 时,y有最小值﹣3 D.当x=﹣2 时,y有最小值﹣3
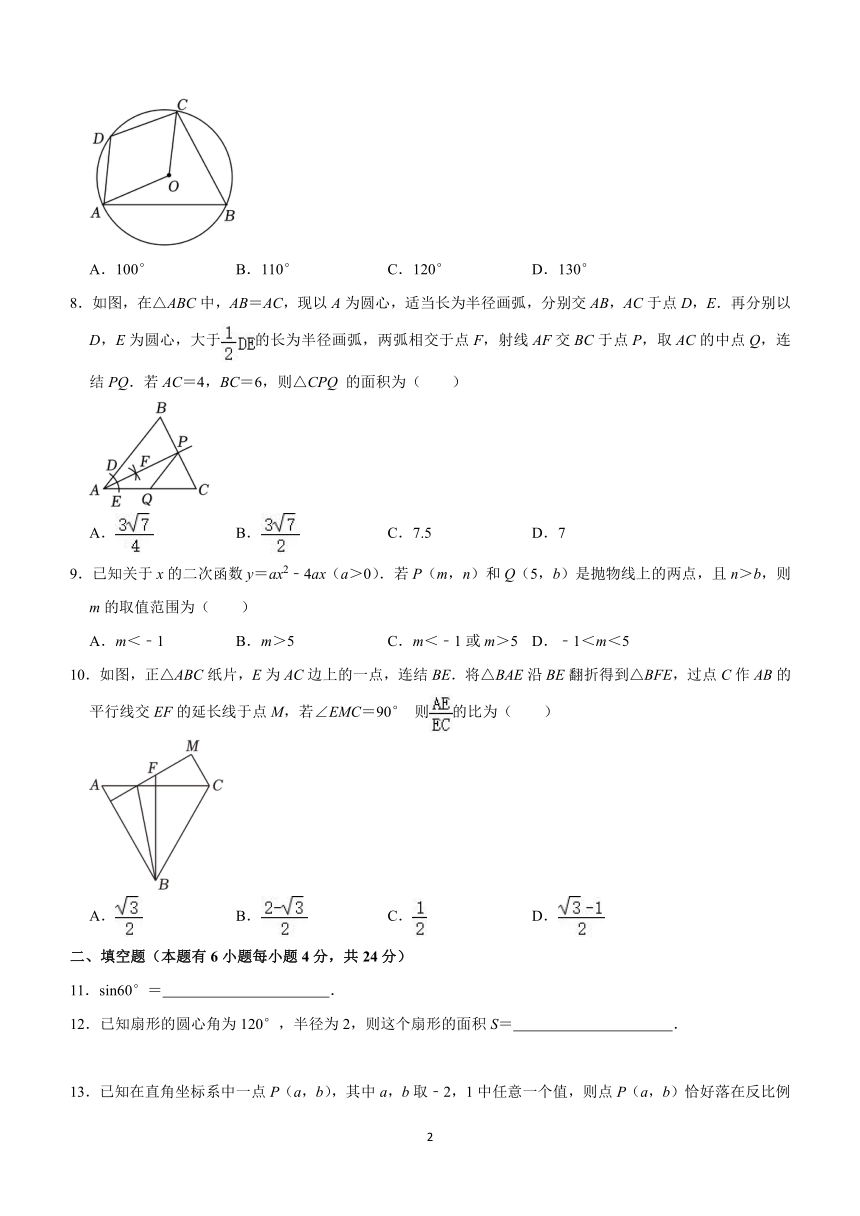
7.如图,已知四边形ABCD内接于⊙O,若∠AOC=140°,则∠ADC等于( )
A.100° B.110° C.120° D.130°
8.如图,在△ABC中,AB=AC,现以A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.再分别以D,E为圆心,大于的长为半径画弧,两弧相交于点F,射线AF交BC于点P,取AC的中点Q,连结PQ.若AC=4,BC=6,则△CPQ 的面积为( )
A. B. C.7.5 D.7
9.已知关于x的二次函数y=ax2﹣4ax(a>0).若P(m,n)和Q(5,b)是抛物线上的两点,且n>b,则m的取值范围为( )
A.m<﹣1 B.m>5 C.m<﹣1或m>5 D.﹣1<m<5
10.如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
二、填空题(本题有6小题每小题4分,共24分)
11.sin60°= .
12.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S= .
13.已知在直角坐标系中一点P(a,b),其中a,b取﹣2,1中任意一个值,则点P(a,b)恰好落在反比例函数的图象上的概率为 .
14.已知y=2x﹣1,且,令S=xy,则函数S的取值范围是 .
15.如图,三个正六边形如图摆放,则sin∠ACB= .
16.数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 ;
(2)若x=2y,则= .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)
17.已知3a=2b,求下列各式的值.
(1); (2).
18.如图,在△ABC中,AB=AC.点D在BC上,点E在AC上,连结AD,DE,且∠B=∠ADE.
(1)求证:△ABD∽△DCE;
(2)若AB=6,BD=2CE,求CD的长.
19.某高速收费站有三个ETC通道(ETC通道是指电子不停车收费的专用车道)A,B,C和一个人工收费通道D.
(1)求一辆办理过ETC卡的汽车经过此收费站时,选择A通道通过的概率;
(2)现有都办理过ETC卡的甲,乙两辆汽车都选择了ETC通道通行,求甲,乙两辆车选择不同ETC通道通过的概率.
20.如图,市交通部门要在宽为22米(即AB=22m)的城北街两边安装路灯(路灯主杆BC垂直于地面),路灯的灯臂CD长2米,路灯采用圆锥形灯罩,灯罩的中心轴线DO与灯臂CD垂直.
(1)探索灯臂CD与灯柱BC 的夹角∠BCD和灯罩中心轴线DO与地面AB所成的夹角∠DOB之间的数量关系;
(2)当灯罩的轴线DO刚好通过街道的中心线(即O为AB的中点)时照明效果最佳,若∠BCD=125°,试说明当灯柱BC=12m时,照明效果是否达到最佳?
(结果保留一位小数)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428)
21.浙教版九上数学课本第24页例1:如图1窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形.如果制作一个窗户边框的材料总长度为6m,那么如何设计这个窗户边框的尺寸,使透光面积最大?这道例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大约为1.05m2.
我们如果改变这个窗户的形状,上部改为一个等边三角形(如图2),材料总长度仍为6m,利用图2,解答下列问题:
(1)当AB=1时,求此时窗户的透光面积;
(2)与课本中例1比较,改变窗户形状后,窗户的透光面积的最大值是否变大?通过计算说明.取1.7)
22.如图.正方形ABCD顶点A,B在⊙O上.BC与⊙O交于点E,CD经过⊙O上一点P,且EP平分∠AEC.
(1)求证:CD是⊙O的切线;
(2)若S正方形ABCD=16,求CE的长.
23.已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
24.如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
一、选择题(本题有10小题,每小题3分,共30分)
1.若△ABC与△DEF的相似比为1:3,则△ABC与△DEF的周长比为( )
A.1:3 B.1:9 C.3:1 D.9:1
2.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.无法确定 B.相切 C.相交 D.相离
3.二次函数y=ax2(a≠0)的图象经过点(2,﹣1),则a的值是( )
A. B. C. D.2
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段BC的长是( )
A. B.1 C. D.2
5.在Rt△ABC中,∠C=90°,cosB=,则tanA=( )
A. B. C. D.
6.关于二次函数y=(x﹣2)2﹣3的最大值或最小值,下列叙述正确的是( )
A.当x=2 时,y有最大值﹣3 B.当x=﹣2 时,y有最大值﹣3
C.当x=2 时,y有最小值﹣3 D.当x=﹣2 时,y有最小值﹣3
7.如图,已知四边形ABCD内接于⊙O,若∠AOC=140°,则∠ADC等于( )
A.100° B.110° C.120° D.130°
8.如图,在△ABC中,AB=AC,现以A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.再分别以D,E为圆心,大于的长为半径画弧,两弧相交于点F,射线AF交BC于点P,取AC的中点Q,连结PQ.若AC=4,BC=6,则△CPQ 的面积为( )
A. B. C.7.5 D.7
9.已知关于x的二次函数y=ax2﹣4ax(a>0).若P(m,n)和Q(5,b)是抛物线上的两点,且n>b,则m的取值范围为( )
A.m<﹣1 B.m>5 C.m<﹣1或m>5 D.﹣1<m<5
10.如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
二、填空题(本题有6小题每小题4分,共24分)
11.sin60°= .
12.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S= .
13.已知在直角坐标系中一点P(a,b),其中a,b取﹣2,1中任意一个值,则点P(a,b)恰好落在反比例函数的图象上的概率为 .
14.已知y=2x﹣1,且,令S=xy,则函数S的取值范围是 .
15.如图,三个正六边形如图摆放,则sin∠ACB= .
16.数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 ;
(2)若x=2y,则= .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程)
17.已知3a=2b,求下列各式的值.
(1); (2).
18.如图,在△ABC中,AB=AC.点D在BC上,点E在AC上,连结AD,DE,且∠B=∠ADE.
(1)求证:△ABD∽△DCE;
(2)若AB=6,BD=2CE,求CD的长.
19.某高速收费站有三个ETC通道(ETC通道是指电子不停车收费的专用车道)A,B,C和一个人工收费通道D.
(1)求一辆办理过ETC卡的汽车经过此收费站时,选择A通道通过的概率;
(2)现有都办理过ETC卡的甲,乙两辆汽车都选择了ETC通道通行,求甲,乙两辆车选择不同ETC通道通过的概率.
20.如图,市交通部门要在宽为22米(即AB=22m)的城北街两边安装路灯(路灯主杆BC垂直于地面),路灯的灯臂CD长2米,路灯采用圆锥形灯罩,灯罩的中心轴线DO与灯臂CD垂直.
(1)探索灯臂CD与灯柱BC 的夹角∠BCD和灯罩中心轴线DO与地面AB所成的夹角∠DOB之间的数量关系;
(2)当灯罩的轴线DO刚好通过街道的中心线(即O为AB的中点)时照明效果最佳,若∠BCD=125°,试说明当灯柱BC=12m时,照明效果是否达到最佳?
(结果保留一位小数)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428)
21.浙教版九上数学课本第24页例1:如图1窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形.如果制作一个窗户边框的材料总长度为6m,那么如何设计这个窗户边框的尺寸,使透光面积最大?这道例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大约为1.05m2.
我们如果改变这个窗户的形状,上部改为一个等边三角形(如图2),材料总长度仍为6m,利用图2,解答下列问题:
(1)当AB=1时,求此时窗户的透光面积;
(2)与课本中例1比较,改变窗户形状后,窗户的透光面积的最大值是否变大?通过计算说明.取1.7)
22.如图.正方形ABCD顶点A,B在⊙O上.BC与⊙O交于点E,CD经过⊙O上一点P,且EP平分∠AEC.
(1)求证:CD是⊙O的切线;
(2)若S正方形ABCD=16,求CE的长.
23.已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
24.如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
同课章节目录
