2015快乐暑假初三升初四复习部分——八年级下册第九章相似图形(2)
文档属性
| 名称 | 2015快乐暑假初三升初四复习部分——八年级下册第九章相似图形(2) |  | |
| 格式 | zip | ||
| 文件大小 | 91.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-24 09:07:58 | ||
图片预览

文档简介
2015快乐暑假初三升初四复习部分——八年级下册第九章相似图形(2)
一、知识梳理
相似三角形的性质:
相似三角形的对应角 ,对应边 。
相似三角形的 、 、 的比都等于 。
相似三角形周长的比等于 ,面积的比等于 。
相似三角形的判定
(1) 的两个三角形相似。
(2) 的两个三角形相似。
(3) 的两个三角形相似。
二、典例解析
1、两个相似三角形的相似比为1:2,其中较小三角形的最大边长为10cm,最小角为20°,则另一个三角形的最大边为 ,最小角 。
2、Rt△ABC的两直角边分别为3cm和4cm,与它相似的Rt△A’B’C’的斜边为20cm,则Rt△A’B’C’的周长是 。
3、(2015春 泰山区期末)如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上。若这个矩形的长是宽的2倍,求矩形的长和宽。
4、(2014 金平区模拟)如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
5、(2014秋 包河区期末)如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
提升训练
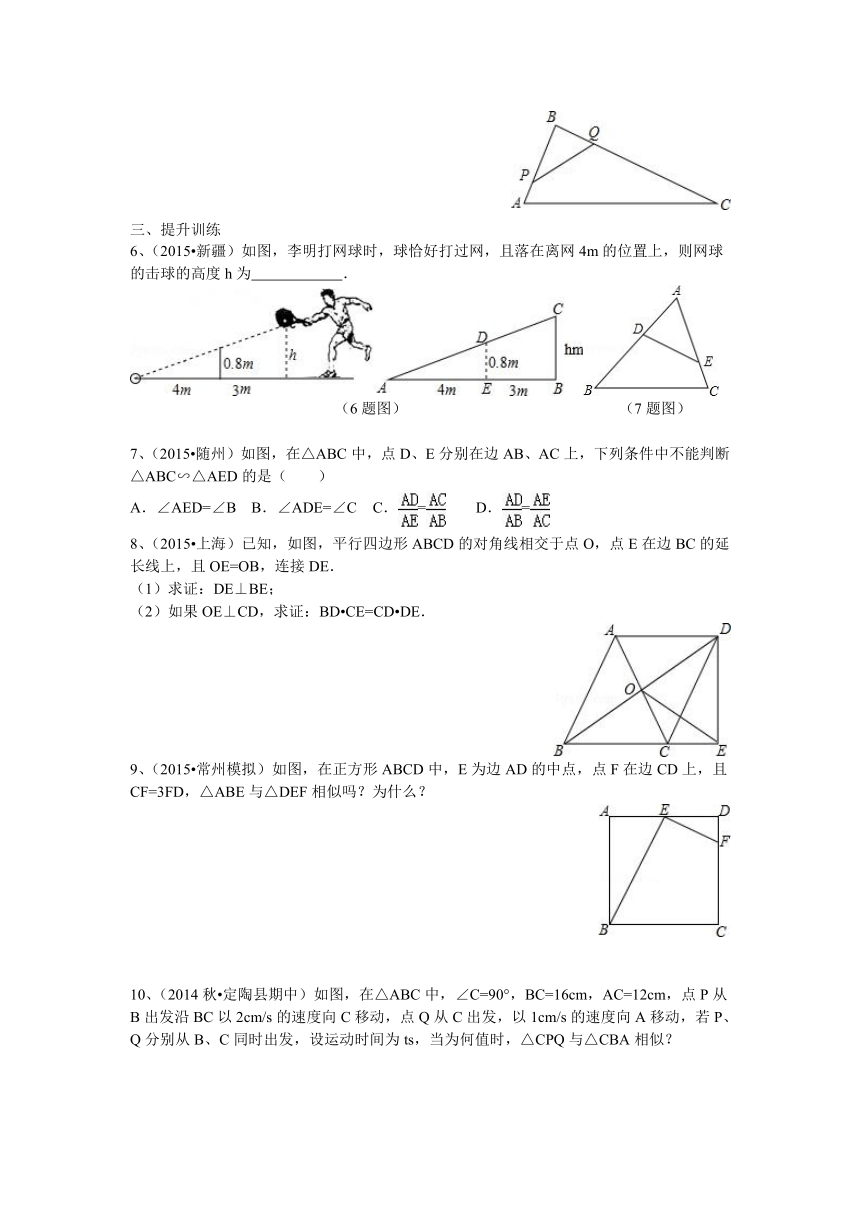
6、(2015 新疆)如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为 .
(6题图) (7题图)
7、(2015 随州)如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C.= D.=
8、(2015 上海)已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD CE=CD DE.
9、(2015 常州模拟)如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?
10、(2014秋 定陶县期中)如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
(2015 广西)一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成两个并排全等的正方形零件如图2,问这个小正方形的边长是多少?并排放置3个小正方形呢?n个呢?说明理由。
参考答案
1、20 2、20°
3、解:如图,∵四边形PQMN为矩形,∴PN∥BC,PQ=DE,∴△APN∽△ABC,
∴=,
设PQ=x,则ED=x,AE=AD﹣DE=8﹣x,
当PN=2PQ时,即PN=2x,则=,解得x=,所以2x=,此时矩形的长、宽分别为,;
当PN=PQ时,即PN=x,则=,解得x=2,所以x=1,此时矩形的长、宽分别为2,1;
所以矩形的长、宽分别为cm,cm或2cm,1cm.
4、(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
5、 解:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴=,即=,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴=,即=,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
6、 1.4 .7、D.
8、证明:(1)∵四边形ABCD是平行四边形,∴BO=BD,
∵OE=OB,∴OE=BD,∴∠BED=90°,∴DE⊥BE;
(2)∵OE⊥CD∴∠CEO+∠DCE=∠CDE+∠DCE=90°,∴∠CEO=∠CDE,
∵OB=OE,∴∠DBE=∠CDE,
∵∠BED=∠BED,∴△BDE∽△CDE,∴,∴BD CE=CD DE.
9、 解:△ABE与△DEF相似.理由如下:
∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为边AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴==2,==2,
∴=,
而∠A=∠D,
∴△ABE∽△DEF.
10、 解:CP和CB是对应边时,△CPQ∽△CBA,
所以,=,
即=,
解得t=4.8;
CP和CA是对应边时,△CPQ∽△CAB,
所以,=,
即=,
解得t=.
综上所述,当t=4.8秒或秒时,△CPQ与△CBA相似.
一、知识梳理
相似三角形的性质:
相似三角形的对应角 ,对应边 。
相似三角形的 、 、 的比都等于 。
相似三角形周长的比等于 ,面积的比等于 。
相似三角形的判定
(1) 的两个三角形相似。
(2) 的两个三角形相似。
(3) 的两个三角形相似。
二、典例解析
1、两个相似三角形的相似比为1:2,其中较小三角形的最大边长为10cm,最小角为20°,则另一个三角形的最大边为 ,最小角 。
2、Rt△ABC的两直角边分别为3cm和4cm,与它相似的Rt△A’B’C’的斜边为20cm,则Rt△A’B’C’的周长是 。
3、(2015春 泰山区期末)如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上。若这个矩形的长是宽的2倍,求矩形的长和宽。
4、(2014 金平区模拟)如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
5、(2014秋 包河区期末)如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
提升训练
6、(2015 新疆)如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为 .
(6题图) (7题图)
7、(2015 随州)如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C.= D.=
8、(2015 上海)已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD CE=CD DE.
9、(2015 常州模拟)如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,△ABE与△DEF相似吗?为什么?
10、(2014秋 定陶县期中)如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
(2015 广西)一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成两个并排全等的正方形零件如图2,问这个小正方形的边长是多少?并排放置3个小正方形呢?n个呢?说明理由。
参考答案
1、20 2、20°
3、解:如图,∵四边形PQMN为矩形,∴PN∥BC,PQ=DE,∴△APN∽△ABC,
∴=,
设PQ=x,则ED=x,AE=AD﹣DE=8﹣x,
当PN=2PQ时,即PN=2x,则=,解得x=,所以2x=,此时矩形的长、宽分别为,;
当PN=PQ时,即PN=x,则=,解得x=2,所以x=1,此时矩形的长、宽分别为2,1;
所以矩形的长、宽分别为cm,cm或2cm,1cm.
4、(1)证明:∵△ABC,△ADE为等边三角形,
∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,
∴∠1=∠DFC,
∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,
∴△AEF∽△DCF,
∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
5、 解:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴=,即=,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴=,即=,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
6、 1.4 .7、D.
8、证明:(1)∵四边形ABCD是平行四边形,∴BO=BD,
∵OE=OB,∴OE=BD,∴∠BED=90°,∴DE⊥BE;
(2)∵OE⊥CD∴∠CEO+∠DCE=∠CDE+∠DCE=90°,∴∠CEO=∠CDE,
∵OB=OE,∴∠DBE=∠CDE,
∵∠BED=∠BED,∴△BDE∽△CDE,∴,∴BD CE=CD DE.
9、 解:△ABE与△DEF相似.理由如下:
∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=AD=CD,
设AB=AD=CD=4a,
∵E为边AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴==2,==2,
∴=,
而∠A=∠D,
∴△ABE∽△DEF.
10、 解:CP和CB是对应边时,△CPQ∽△CBA,
所以,=,
即=,
解得t=4.8;
CP和CA是对应边时,△CPQ∽△CAB,
所以,=,
即=,
解得t=.
综上所述,当t=4.8秒或秒时,△CPQ与△CBA相似.
