2024年江苏省徐州市中考数学一模考前练习卷(含解析)
文档属性
| 名称 | 2024年江苏省徐州市中考数学一模考前练习卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 17:16:51 | ||
图片预览


文档简介
2024江苏省徐州市九年级中考数学一模考前练习卷
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.温度由上升后是( )
A. B. C. D.
2. 下列图形中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
3. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. B. C. D.
4. 下列计算正确的是( )
A.2a+3b=5ab B.x8÷x2=x6 C.(ab3)2=ab6 D.(x+2)2=x2+4
为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,
调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,
则所调查学生睡眠时间的众数,中位数分别为( )
A.7 h;7 h B.8 h;7.5 h C.7 h ;7.5 h D.8 h;8 h
6. 估算的值( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.无法确定
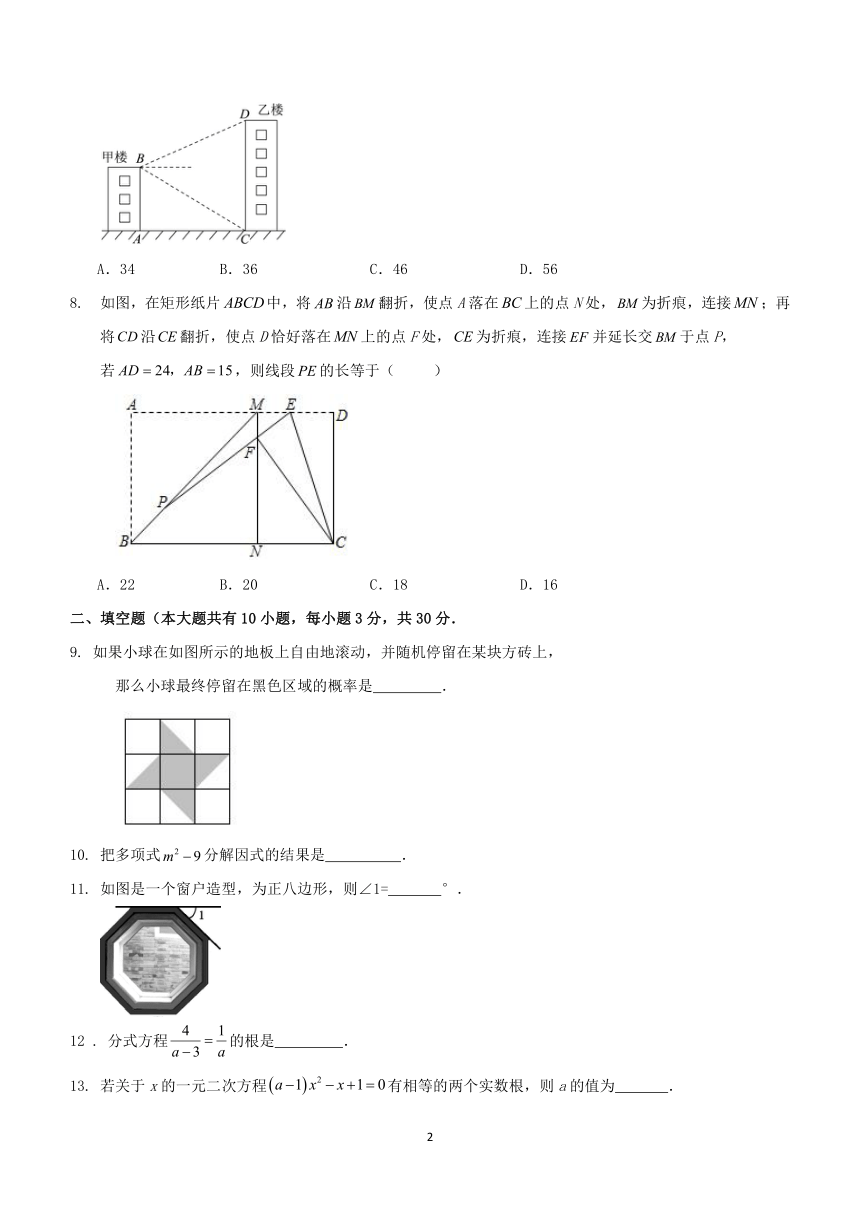
7 . 如图,甲、乙两楼的距离AC=30m,甲楼高AB=20m,自甲楼楼顶的B处看乙楼楼顶的D处,
仰角为28°,则乙楼的高CD为( )m.
(结果精确到1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
A.34 B.36 C.46 D.56
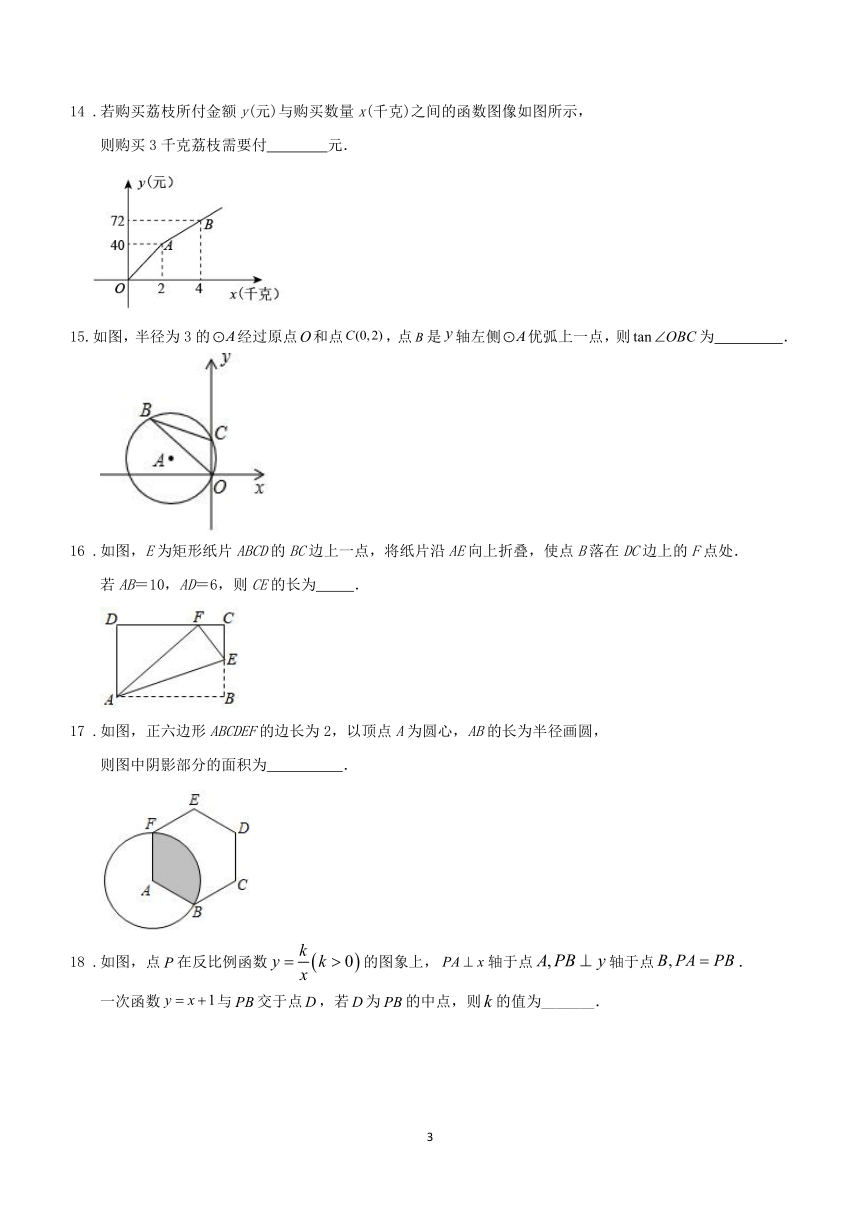
如图,在矩形纸片中,将沿翻折,使点A落在上的点N处,为折痕,连接;再将沿翻折,使点D恰好落在上的点F处,为折痕,连接并延长交于点P,
若,则线段的长等于( )
A.22 B.20 C.18 D.16
填空题(本大题共有10小题,每小题3分,共30分.
9. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,
那么小球最终停留在黑色区域的概率是 .
10. 把多项式分解因式的结果是 .
11. 如图是一个窗户造型,为正八边形,则∠1= °.
12 . 分式方程的根是 .
13. 若关于x的一元二次方程有相等的两个实数根,则a的值为 .
14 .若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
15.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则为 .
16 .如图,E为矩形纸片ABCD的BC边上一点,将纸片沿AE向上折叠,使点B落在DC边上的F点处.
若AB=10,AD=6,则CE的长为 .
17 .如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
18 .如图,点在反比例函数的图象上,轴于点轴于点.
一次函数与交于点,若为的中点,则的值为_______.
三、解答题(本大题共有10小题,共86分.)
19. (1)计算:;
(2)解方程:.
20. (1)解方程:;
(2)解不等式组:
为了解某地区九年级学生的视力情况,从该地区九年级学生中抽查了部分学生,
根据调查结果,绘制了如下两幅不完整的统计图.
根据以上信息,解决下列问题:
(1)此次调查的样本容量为 ;
(2)扇形统计图中对应圆心角的度数为 °;
(3)请补全条形统计图;
(4)若该地区九年级学生共有人,请估计其中视力正常的人数.
甲,乙、丙三人到淮海战役烈士纪念塔园林游览,
若每人分别从纪念塔、纪念馆这两个景点中选择一个参观,且选择每个景点的机会相等,
则三人选择相同景点的概率为多少?
23. 如图,在菱形中,、分别是、的中点.
求证;
(2) 若菱形的面积为8,则的面积为______.
24 . 2022年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,
12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.
求“冰墩墩”和“雪容融”的销售单价;
已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,
这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,
其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,
则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.
25 . 如图,图1是一盏台灯,图2是其侧面示意图(台灯底座高度忽略不计),
其中灯臂,灯罩,灯臂与底座构成的.
可以绕点上下调节一定的角度.使用发现:当与水平线所成的角为时,
台灯光线最佳,求此时点与桌面的距离.(结果精确到,取1.732)
26 . 如图,在中,,O是上一点,
以为半径的与相切于点D,与相交于点E.
求证:是的平分线;
若,,求的长.
27 . 【发现问题】
如图1,已知和均为等边三角形,在上,在上,
易得线段和的数量关系是______.
将图1中的绕点旋转到图2的位置,直线和直线交于点.
① 判断线段和的数量关系,并证明你的结论;
② 图2中的度数是______.
(3)【探究拓展】
如图3,若和均为等腰直角三角形,,,,
直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
28 . 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,
点P是抛物线上一动点,连接PB,PC.
(1)求抛物线的解析式;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
2024江苏省徐州市九年级中考数学一模考前练习卷
答案解析
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.温度由上升后是( )
A. B. C. D.
【答案】A
【分析】根据用上升的温度减去原来的温度列出式子,求出最后的结果即可.
【详解】解:(),
故选:A.
2. 下列图形中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解.
【详解】A、是轴对称图形,也是中心对称图形,故本选项符合题意,
B、是轴对称图形,不是中心对称图形,故本选项不合题意,
C、不是轴对称图形,是中心对称图形,故本选项不合题意,
D、是轴对称图形,不是中心对称图形,故本选项不合题意,
故选:A.
3. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】由数轴可知,,可判断A的正误;
根据,可判断B的正误;根据,可判断C的正误;
根据,,可判断D的正误.
【详解】解:由数轴可知,,
∴,故A错误,不符合题意;
∵,
∴,故B错误,不符合题意;
∵,
∴,故C错误,不符合题意;
∵,,
∴,故D正确,符合题意;
故选D.
4. 下列计算正确的是( )
A.2a+3b=5ab B.x8÷x2=x6 C.(ab3)2=ab6 D.(x+2)2=x2+4
【答案】B
【分析】由相关运算法则计算判断即可.
【详解】2a和3b不是同类项,无法计算,与题意不符,故错误;
x8÷x2=x6,与题意相符,故正确;
(ab3)2=a2b6,与题意不符,故错误;
(x+2)2=x2+2x+4,与题意不符,故错误.
故选:B.
为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,
调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,
则所调查学生睡眠时间的众数,中位数分别为( )
A.7 h;7 h B.8 h;7.5 h C.7 h ;7.5 h D.8 h;8 h
【答案】C
【分析】根据众数的定义及所给频数分布直方图可知,睡眠时间为7小时的人数最多,根据中位数的定义,把睡眠时间按从小到大排列,第25和26位学生的睡眠时间的平均数是中位数,从而可得结果.
【详解】由频数分布直方图知,睡眠时间为7小时的人数最多,从而众数为7h;
把睡眠时间按从小到大排列,第25和26位学生的睡眠时间的平均数是中位数,
而第25位学生的睡眠时间为7h,第26位学生的睡眠时间为8h,其平均数为7.5h,
故选:C.
6. 估算的值( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.无法确定
【答案】A
【分析】根据的范围,即可得出答案.
【详解】∵,∴,故在2和3之间.故选A.
7 . 如图,甲、乙两楼的距离AC=30m,甲楼高AB=20m,自甲楼楼顶的B处看乙楼楼顶的D处,
仰角为28°,则乙楼的高CD为( )m.
(结果精确到1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
A.34 B.36 C.46 D.56
【答案】B
【分析】过点B作BE⊥CD于点E,则CE=AB=20m,BE=AC=30m,在中,
由,可得,即可求解.
【详解】解:如图,过点B作BE⊥CD于点E,则CE=AB=20m,BE=AC=30m,
根据题意得:∠DBE=28°,
在中,,
∴,
解得:,
∴.
故选:B.
如图,在矩形纸片中,将沿翻折,使点A落在上的点N处,为折痕,连接;再将沿翻折,使点D恰好落在上的点F处,为折痕,连接并延长交于点P,
若,则线段的长等于( )
A.22 B.20 C.18 D.16
【答案】B
【分析】根据折叠可得是正方形,,可求出三角形的三边为9,12,15,在中,由勾股定理可以求出三边的长,通过作辅助线,可证,三边占比为,设未知数,通过,列方程求出待定系数,进而求出的长,然后求的长.
【详解】解:过点P作,垂足为G、H,
由折叠得:是正方形,,
,
∴,
在中,,
∴,
在中,设,则,由勾股定理得,,
解得:,
∵,
∴,
∵,
∴,
∴,
设,则,
∴,
解得:,
∴,
∴,
故选:B.
填空题(本大题共有10小题,每小题3分,共30分.
9. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,
那么小球最终停留在黑色区域的概率是 .
【答案】
【分析】先计算黑色区域的面积,根据黑色方砖占总方砖的比例可得出概念.
【详解】解:∵由图可知,黑色方砖有块,共有块方砖,
∴黑色方砖在整个地板中所占的比值,
∴小球最终停留在黑色区域的概率是,
故答案为:.
10. 把多项式分解因式的结果是 .
【答案】/
【分析】根据平方差公式分解因式即可.
【详解】解:.
故答案为:.
11. 如图是一个窗户造型,为正八边形,则∠1= °.
【答案】45°
【分析】根据正多边形的内角和公式即可求解.
【详解】∵图形为正八边形
∴内角为=135°,
∴∠1=180°-135°=45°.
12 . 分式方程的根是 .
【答案】
【详解】试题解析:去分母得:4a-a+3=0,
解得:a=-1,
经检验a=-1是分式方程的解.
13. 若关于x的一元二次方程有相等的两个实数根,则a的值为 .
【答案】
【分析】根据一元二次方程根的判别式的意义得到且,然后解一次方程可得到的值.
【详解】解:根据题意得且,
解得.
故答案为:.
14 .若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
【答案】
【分析】根据图像可得购买3kg荔枝需要付的钱即为当x=3时,y所对应的值,即求出AB段的函数解析式,将x=3代入即可.
【详解】解:设直线的解析式为:,
由图像可知:,
∴,
∴,
当时,,
故答案为:.
15.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则为 .
【答案】
【分析】连接CD,根据90°圆周角所对的弦是圆的直径,确定CD,根据勾股定理计算DO,根据同弧上的圆周角相等,计算tan∠ODC即可
【详解】如图,连接CD,
∵∠DOC=90°,
∴CD是圆A的直径,
∵半径为3的经过原点和点,
∴CD=6,OC=2,
∴DO==,
∴tan∠ODC==,
∵∠ODC=∠OBC,
∴tan∠OBC=,
故答案为:.
16 .如图,E为矩形纸片ABCD的BC边上一点,将纸片沿AE向上折叠,使点B落在DC边上的F点处.
若AB=10,AD=6,则CE的长为 .
【答案】
【分析】根据折叠的性质可以得到EF=BE,AF=AB=10,根据勾股定理可得DF=8,求的CF=2,再在Rt△CEF中,根据勾股定理建立方程即可求解.
【详解】解:∵将矩形ABCD沿AE向上折叠,使点B落在DC边上的F点处,AB=10,
∴EF=BE,AF=AB=10,
在矩形ABCD中,CD=AB=10,BC=AD=6,
在Rt△ADF中,DF==8,
∴CF=2,
在Rt△CEF中,EF2=CE2+CF2,
设CE=x,
∴(6﹣CE)2=CE2+22,即(6﹣x)2=x2+22,
解得x=,
则CE=.
故答案为:.
17 .如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
【答案】
【分析】延长FA交⊙A于G,如图所示:根据六边形ABCDEF是正六边形,AB=2,利用外角和求得∠GAB=,再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°, 利用扇形面积公式代入数值计算即可.
【详解】解:延长FA交⊙A于G,如图所示:
∵六边形ABCDEF是正六边形,AB=2,
∴∠GAB=,
∠FAB=180°-∠GAB=180°-60°=120°,
∴,
故答案为.
18 .如图,点在反比例函数的图象上,轴于点轴于点.
一次函数与交于点,若为的中点,则的值为_______.
【答案】4
【解析】
【分析】根据题意可设点P的坐标为,则,
把代入一次函数解析式中求出m的值进而求出点P的坐标,再求出k的值即可.
【详解】解:∵轴于点轴于点,
∴点P的横纵坐标相同,
∴可设点P的坐标为,
∵为的中点,
∴,
∵在直线上,
∴,
∴,
∴,
∵点在反比例函数的图象上,
∴,
故答案为:4.
三、解答题(本大题共有10小题,共86分.)
19. (1)计算:;
(2)解方程:.
【答案】(1)1;(2)
【分析】(1)先根据零指数幂、绝对值的性质、特殊角的三角函数值、负整数指数幂的意义化简,再算加减即可;
(2)两边都乘以化为整式方程求解,然后检验即可.
【详解】解:(1)原式
;
(2),
两边都乘以,得
,
解得,
检验:当时,,
∴原方程的解.
20. (1)解方程:;
(2)解不等式组:
【答案】(1);(2)
【分析】(1)根据配方法解一元二次方程即可求解;
分别求出每一个不等式的解集,根据口诀:
同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】(1)解:,
,
∴,
;
(2)解:,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
为了解某地区九年级学生的视力情况,从该地区九年级学生中抽查了部分学生,
根据调查结果,绘制了如下两幅不完整的统计图.
根据以上信息,解决下列问题:
(1)此次调查的样本容量为 ;
(2)扇形统计图中对应圆心角的度数为 °;
(3)请补全条形统计图;
(4)若该地区九年级学生共有人,请估计其中视力正常的人数.
【答案】(1)450 (2)
(3)见解析 (4)人
【解析】
【分析】(1)根据的人数是人,所占的比例是,据此即可求得此次调查的样本容量;
(2)用类学生数除以,再乘以即可得解;
(3)利用总人数减去、、三类的人数即可求得的人数,从而补全直方图;
(4)利用总人数乘以对应的百分比即可求得.
【小问1详解】
解:,
答:此次调查的样本容量为是,
故答案为.
【小问2详解】
解:,
故答案为;
【小问3详解】
解:
补全图形如下:
【小问4详解】
解:(人)
答:九年级学生共有人,请估计其中视力正常的人数共有人.
甲,乙、丙三人到淮海战役烈士纪念塔园林游览,
若每人分别从纪念塔、纪念馆这两个景点中选择一个参观,且选择每个景点的机会相等,
则三人选择相同景点的概率为多少?
【答案】
【解析】
【分析】根据树状图可进行求解概率.
【详解】解:由题意可得如下树状图:
∴甲、乙、丙三人分别从纪念塔、纪念馆这两个景点中选择一个参观,则共有8种情况,
其中三人选择相同景点参观共有2种,所以三人选择相同景点的概率为.
23. 如图,在菱形中,、分别是、的中点.
求证;
(2) 若菱形的面积为8,则的面积为______.
【答案】(1)见解析
(2)3
【分析】(1) 由四边形ABCD是菱形,即可求得AB=AD,∠B=∠D,又由、分别是、的中点可证得BE=DF,根据SAS,即可证△ABE≌△ADF得AE=AF,从而得证.
(2) 连接AC、BD,交于点O,AC交EF于点G,根据菱形性质可得菱形面积公式,然后根据三角形中位线定理得EF与BD关系,最后根据三角形面积公式代入计算可得答案.
【详解】(1)证明:∵四边形ABCD是菱形,
∴AB=AD,BC=DC,∠B=∠D,
∵、分别是、的中点,
∴,,
∴BE=DF,
在△ABE和△ADF中
,
∴△ABE≌△ADF(SAS);
∴AE=AF,
∴∠AEF=∠AFE.
(2)连接AC、BD,交于点O,AC交EF于点G,
∵四边形ABCD是菱形,
∴AO=OC,菱形ABCD的面积为:,
∵点E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴AC⊥EF,AG=3CG,
设AC=a,BD=b,
∴,即ab=16,
∴.
故答案为:3
24 . 2022年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,
12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.
求“冰墩墩”和“雪容融”的销售单价;
已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,
这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,
其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,
则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.
【答案】(1)“冰墩墩”和“雪容融”的销售单价分别为120元和80元;
(2)当“冰墩墩”购进200个时该旗舰店当月销售利润最大,最大利润为11600元.
【分析】(1)根据题意,列二元一次方程组即可;
(2)根据题意,列一元一次不等式组,求出m的解集,表示出月销售利润w=-2m+12000,根据函数增减性即可求出最大利润.
【详解】(1)解:设“冰墩墩”和“雪容融”的销售单价分别为x元,y元,
根据题意得,
解得,
答:“冰墩墩”和“雪容融”的销售单价分别为120元和80元;
(2)解:设“冰墩墩”购进m个时该旗舰店当月销售利润最大,此时“雪容融”购进了(600-m)个,
根据题意,得600-m≤2m,
解不等式得m≥200,
设该旗舰店当月销售利润w=(120-102)m+(80-60)(600-m)=-2m+12000,
∵-2<0,
∴w随着m的增大而减小,
∴当m=200时,w最大=-400+12000=11600,
答:当“冰墩墩”购进200个时该旗舰店当月销售利润最大,最大利润为11600元.
25 . 如图,图1是一盏台灯,图2是其侧面示意图(台灯底座高度忽略不计),
其中灯臂,灯罩,灯臂与底座构成的.
可以绕点上下调节一定的角度.使用发现:当与水平线所成的角为时,
台灯光线最佳,求此时点与桌面的距离.(结果精确到,取1.732)
【答案】
【分析】过点作,交延长线于点,过点作于F,过点作于E,
分别在和中,利用锐角三角函数的知识求出和的长,再由矩形的判定和性质得到,最后根据线段的和差计算出的长,问题得解.
【详解】过点作,交延长线于点,过点作于F,过点作于E,
在中,,,
∵
∴(cm),
在中,,,
∵,
∴(cm),
∵,,,
∴四边形是矩形,
∴,
∵,
∴(cm).
答:点与桌面的距离约为.
26 . 如图,在中,,O是上一点,
以为半径的与相切于点D,与相交于点E.
求证:是的平分线;
若,,求的长.
【答案】(1)见解析
(2)6
【分析】(1)根据切线的性质得,再由,得,由平行线的性质得,又因为等腰三角形得,等量代换即可得证;
(2)在中,由勾股定理即可求半径.
【详解】(1)证明:连接OD;
∵与BC相切于点D
∴
∴
∵,
∴
∴
∴
∵
∴
∴
∴是的平分线;
(2)解:∵
∴在中;
∵,
,
设圆的半径为r,
∴
解得,
∴圆的半径为3
∴.
27 . 【发现问题】
如图1,已知和均为等边三角形,在上,在上,
易得线段和的数量关系是______.
将图1中的绕点旋转到图2的位置,直线和直线交于点.
① 判断线段和的数量关系,并证明你的结论;
② 图2中的度数是______.
(3)【探究拓展】
如图3,若和均为等腰直角三角形,,,,
直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
【答案】(1)
(2)①,证明见解析;②;
(3)度,,理由见解析
【分析】(1)由等腰三角形的性质可求解;
(2)①由“SAS”可证,可得;
②由全等三角形的性质可得,即可解决问题.
结论:,.证明,
可得,,由此即可解决问题.
【详解】(1)解:∵和均为等边三角形,
∴,,
∴,
故答案为:;
(2)如图2中,
①∵和均为等边三角形,
∴,,,
∴,
∴(SAS),
∴;
②∵,
∴,
设交于点.
∵,
∴,
∴,
故答案为:;
(3)结论:,.
理由:如图3中,
∵,,,
∴,,
∴,
∴,,
∴,
∵,
∴.
28 . 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,
点P是抛物线上一动点,连接PB,PC.
(1)求抛物线的解析式;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)3;(3)点P的坐标为(1,4)或(﹣2,﹣5)
【分析】(1)用待定系数法求解即可;
(2)先求得点C的坐标,再用待定系数法求得直线BC的解析式;由PE=2ED可得PD=3ED,设P(m,﹣m2+2m+3),则E(m,﹣m+3),用含m的式子表示出PD和DE,根据PD=3ED得出关于m的方程,解得m的值,则可得PE的长,然后按照三角形的面积公式计算即可;
(3)分两种情况:①点C为直角顶点;②点B为直角顶点.过点C作直线P1C⊥BC,交抛物线于点P1,连接P1B,交x轴于点D;过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,分别求得直线P1C和直线BP2的解析式,将它们分别与抛物线的解析式联立,即可求得点P的坐标.
【详解】解:(1)∵抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)在y=﹣x2+2x+3中,当x=0时,y=3,
∴C(0,3).
设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入,得:
,
解得,
∴直线BC的解析式为y=﹣x+3,
若PE=2ED,则PD=3ED,
设P(m,﹣m2+2m+3),
∵PD上x轴于点D,
∴E(m,﹣m+3),
∴﹣m2+2m+3=3(﹣m+3),
∴m2﹣5m+6=0,
解得m1=2,m2=3(舍),
∴m=2,此时P(2,3),E(2,1),
∴PE=2,
∴S△PBC=×2×3=3.
∴△PBC的面积为3;
(3)∵△PBC是以BC为直角边的直角三角形,
∴有两种情况:①点C为直角顶点;②点B为直角顶点.
过点C作直线P1C⊥BC,交抛物线于点P1,连接P1B,交x轴于点D;
过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,如图所示:
∵B(3,0),C(0,3),
∴OB=OC=3,
∴∠BCO=∠OBC=45°.
∵P1C⊥BC,
∴∠DCB=90°,
∴∠DCO=45°,
又∵∠DOC=90°,
∴∠ODC=45°=∠DCO,
∴OD=OC=3,
∴D(﹣3,0),
∴直线P1C的解析式为y=x+3,
联立,
解得或(舍);
∴P1(1,4);
∵P1C⊥BC,BP2⊥BC,
∴P1CBP2,
∴设直线BP2的解析式为y=x+b,
将B(3,0)代入,得0=3+b,
∴b=﹣3,
∴直线BP2的解析式为y=x﹣3,
联立,
解得或(舍),
∴P2(﹣2,﹣5).
综上,点P的坐标为(1,4)或(﹣2,﹣5).
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.温度由上升后是( )
A. B. C. D.
2. 下列图形中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
3. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. B. C. D.
4. 下列计算正确的是( )
A.2a+3b=5ab B.x8÷x2=x6 C.(ab3)2=ab6 D.(x+2)2=x2+4
为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,
调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,
则所调查学生睡眠时间的众数,中位数分别为( )
A.7 h;7 h B.8 h;7.5 h C.7 h ;7.5 h D.8 h;8 h
6. 估算的值( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.无法确定
7 . 如图,甲、乙两楼的距离AC=30m,甲楼高AB=20m,自甲楼楼顶的B处看乙楼楼顶的D处,
仰角为28°,则乙楼的高CD为( )m.
(结果精确到1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
A.34 B.36 C.46 D.56
如图,在矩形纸片中,将沿翻折,使点A落在上的点N处,为折痕,连接;再将沿翻折,使点D恰好落在上的点F处,为折痕,连接并延长交于点P,
若,则线段的长等于( )
A.22 B.20 C.18 D.16
填空题(本大题共有10小题,每小题3分,共30分.
9. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,
那么小球最终停留在黑色区域的概率是 .
10. 把多项式分解因式的结果是 .
11. 如图是一个窗户造型,为正八边形,则∠1= °.
12 . 分式方程的根是 .
13. 若关于x的一元二次方程有相等的两个实数根,则a的值为 .
14 .若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
15.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则为 .
16 .如图,E为矩形纸片ABCD的BC边上一点,将纸片沿AE向上折叠,使点B落在DC边上的F点处.
若AB=10,AD=6,则CE的长为 .
17 .如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
18 .如图,点在反比例函数的图象上,轴于点轴于点.
一次函数与交于点,若为的中点,则的值为_______.
三、解答题(本大题共有10小题,共86分.)
19. (1)计算:;
(2)解方程:.
20. (1)解方程:;
(2)解不等式组:
为了解某地区九年级学生的视力情况,从该地区九年级学生中抽查了部分学生,
根据调查结果,绘制了如下两幅不完整的统计图.
根据以上信息,解决下列问题:
(1)此次调查的样本容量为 ;
(2)扇形统计图中对应圆心角的度数为 °;
(3)请补全条形统计图;
(4)若该地区九年级学生共有人,请估计其中视力正常的人数.
甲,乙、丙三人到淮海战役烈士纪念塔园林游览,
若每人分别从纪念塔、纪念馆这两个景点中选择一个参观,且选择每个景点的机会相等,
则三人选择相同景点的概率为多少?
23. 如图,在菱形中,、分别是、的中点.
求证;
(2) 若菱形的面积为8,则的面积为______.
24 . 2022年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,
12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.
求“冰墩墩”和“雪容融”的销售单价;
已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,
这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,
其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,
则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.
25 . 如图,图1是一盏台灯,图2是其侧面示意图(台灯底座高度忽略不计),
其中灯臂,灯罩,灯臂与底座构成的.
可以绕点上下调节一定的角度.使用发现:当与水平线所成的角为时,
台灯光线最佳,求此时点与桌面的距离.(结果精确到,取1.732)
26 . 如图,在中,,O是上一点,
以为半径的与相切于点D,与相交于点E.
求证:是的平分线;
若,,求的长.
27 . 【发现问题】
如图1,已知和均为等边三角形,在上,在上,
易得线段和的数量关系是______.
将图1中的绕点旋转到图2的位置,直线和直线交于点.
① 判断线段和的数量关系,并证明你的结论;
② 图2中的度数是______.
(3)【探究拓展】
如图3,若和均为等腰直角三角形,,,,
直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
28 . 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,
点P是抛物线上一动点,连接PB,PC.
(1)求抛物线的解析式;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
2024江苏省徐州市九年级中考数学一模考前练习卷
答案解析
一、选择题(本大题共有8小题,每小题3分,共24分.)
1.温度由上升后是( )
A. B. C. D.
【答案】A
【分析】根据用上升的温度减去原来的温度列出式子,求出最后的结果即可.
【详解】解:(),
故选:A.
2. 下列图形中,既是轴对称又是中心对称图形的是( )
A. B. C. D.
【答案】A
【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解.
【详解】A、是轴对称图形,也是中心对称图形,故本选项符合题意,
B、是轴对称图形,不是中心对称图形,故本选项不合题意,
C、不是轴对称图形,是中心对称图形,故本选项不合题意,
D、是轴对称图形,不是中心对称图形,故本选项不合题意,
故选:A.
3. 实数a,b在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. B. C. D.
【答案】D
【分析】由数轴可知,,可判断A的正误;
根据,可判断B的正误;根据,可判断C的正误;
根据,,可判断D的正误.
【详解】解:由数轴可知,,
∴,故A错误,不符合题意;
∵,
∴,故B错误,不符合题意;
∵,
∴,故C错误,不符合题意;
∵,,
∴,故D正确,符合题意;
故选D.
4. 下列计算正确的是( )
A.2a+3b=5ab B.x8÷x2=x6 C.(ab3)2=ab6 D.(x+2)2=x2+4
【答案】B
【分析】由相关运算法则计算判断即可.
【详解】2a和3b不是同类项,无法计算,与题意不符,故错误;
x8÷x2=x6,与题意相符,故正确;
(ab3)2=a2b6,与题意不符,故错误;
(x+2)2=x2+2x+4,与题意不符,故错误.
故选:B.
为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,
调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,
则所调查学生睡眠时间的众数,中位数分别为( )
A.7 h;7 h B.8 h;7.5 h C.7 h ;7.5 h D.8 h;8 h
【答案】C
【分析】根据众数的定义及所给频数分布直方图可知,睡眠时间为7小时的人数最多,根据中位数的定义,把睡眠时间按从小到大排列,第25和26位学生的睡眠时间的平均数是中位数,从而可得结果.
【详解】由频数分布直方图知,睡眠时间为7小时的人数最多,从而众数为7h;
把睡眠时间按从小到大排列,第25和26位学生的睡眠时间的平均数是中位数,
而第25位学生的睡眠时间为7h,第26位学生的睡眠时间为8h,其平均数为7.5h,
故选:C.
6. 估算的值( )
A.在2和3之间 B.在3和4之间 C.在4和5之间 D.无法确定
【答案】A
【分析】根据的范围,即可得出答案.
【详解】∵,∴,故在2和3之间.故选A.
7 . 如图,甲、乙两楼的距离AC=30m,甲楼高AB=20m,自甲楼楼顶的B处看乙楼楼顶的D处,
仰角为28°,则乙楼的高CD为( )m.
(结果精确到1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
A.34 B.36 C.46 D.56
【答案】B
【分析】过点B作BE⊥CD于点E,则CE=AB=20m,BE=AC=30m,在中,
由,可得,即可求解.
【详解】解:如图,过点B作BE⊥CD于点E,则CE=AB=20m,BE=AC=30m,
根据题意得:∠DBE=28°,
在中,,
∴,
解得:,
∴.
故选:B.
如图,在矩形纸片中,将沿翻折,使点A落在上的点N处,为折痕,连接;再将沿翻折,使点D恰好落在上的点F处,为折痕,连接并延长交于点P,
若,则线段的长等于( )
A.22 B.20 C.18 D.16
【答案】B
【分析】根据折叠可得是正方形,,可求出三角形的三边为9,12,15,在中,由勾股定理可以求出三边的长,通过作辅助线,可证,三边占比为,设未知数,通过,列方程求出待定系数,进而求出的长,然后求的长.
【详解】解:过点P作,垂足为G、H,
由折叠得:是正方形,,
,
∴,
在中,,
∴,
在中,设,则,由勾股定理得,,
解得:,
∵,
∴,
∵,
∴,
∴,
设,则,
∴,
解得:,
∴,
∴,
故选:B.
填空题(本大题共有10小题,每小题3分,共30分.
9. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,
那么小球最终停留在黑色区域的概率是 .
【答案】
【分析】先计算黑色区域的面积,根据黑色方砖占总方砖的比例可得出概念.
【详解】解:∵由图可知,黑色方砖有块,共有块方砖,
∴黑色方砖在整个地板中所占的比值,
∴小球最终停留在黑色区域的概率是,
故答案为:.
10. 把多项式分解因式的结果是 .
【答案】/
【分析】根据平方差公式分解因式即可.
【详解】解:.
故答案为:.
11. 如图是一个窗户造型,为正八边形,则∠1= °.
【答案】45°
【分析】根据正多边形的内角和公式即可求解.
【详解】∵图形为正八边形
∴内角为=135°,
∴∠1=180°-135°=45°.
12 . 分式方程的根是 .
【答案】
【详解】试题解析:去分母得:4a-a+3=0,
解得:a=-1,
经检验a=-1是分式方程的解.
13. 若关于x的一元二次方程有相等的两个实数根,则a的值为 .
【答案】
【分析】根据一元二次方程根的判别式的意义得到且,然后解一次方程可得到的值.
【详解】解:根据题意得且,
解得.
故答案为:.
14 .若购买荔枝所付金额y(元)与购买数量x(千克)之间的函数图像如图所示,
则购买3千克荔枝需要付 元.
【答案】
【分析】根据图像可得购买3kg荔枝需要付的钱即为当x=3时,y所对应的值,即求出AB段的函数解析式,将x=3代入即可.
【详解】解:设直线的解析式为:,
由图像可知:,
∴,
∴,
当时,,
故答案为:.
15.如图,半径为3的经过原点和点,点是轴左侧优弧上一点,则为 .
【答案】
【分析】连接CD,根据90°圆周角所对的弦是圆的直径,确定CD,根据勾股定理计算DO,根据同弧上的圆周角相等,计算tan∠ODC即可
【详解】如图,连接CD,
∵∠DOC=90°,
∴CD是圆A的直径,
∵半径为3的经过原点和点,
∴CD=6,OC=2,
∴DO==,
∴tan∠ODC==,
∵∠ODC=∠OBC,
∴tan∠OBC=,
故答案为:.
16 .如图,E为矩形纸片ABCD的BC边上一点,将纸片沿AE向上折叠,使点B落在DC边上的F点处.
若AB=10,AD=6,则CE的长为 .
【答案】
【分析】根据折叠的性质可以得到EF=BE,AF=AB=10,根据勾股定理可得DF=8,求的CF=2,再在Rt△CEF中,根据勾股定理建立方程即可求解.
【详解】解:∵将矩形ABCD沿AE向上折叠,使点B落在DC边上的F点处,AB=10,
∴EF=BE,AF=AB=10,
在矩形ABCD中,CD=AB=10,BC=AD=6,
在Rt△ADF中,DF==8,
∴CF=2,
在Rt△CEF中,EF2=CE2+CF2,
设CE=x,
∴(6﹣CE)2=CE2+22,即(6﹣x)2=x2+22,
解得x=,
则CE=.
故答案为:.
17 .如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,
则图中阴影部分的面积为 .
【答案】
【分析】延长FA交⊙A于G,如图所示:根据六边形ABCDEF是正六边形,AB=2,利用外角和求得∠GAB=,再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°, 利用扇形面积公式代入数值计算即可.
【详解】解:延长FA交⊙A于G,如图所示:
∵六边形ABCDEF是正六边形,AB=2,
∴∠GAB=,
∠FAB=180°-∠GAB=180°-60°=120°,
∴,
故答案为.
18 .如图,点在反比例函数的图象上,轴于点轴于点.
一次函数与交于点,若为的中点,则的值为_______.
【答案】4
【解析】
【分析】根据题意可设点P的坐标为,则,
把代入一次函数解析式中求出m的值进而求出点P的坐标,再求出k的值即可.
【详解】解:∵轴于点轴于点,
∴点P的横纵坐标相同,
∴可设点P的坐标为,
∵为的中点,
∴,
∵在直线上,
∴,
∴,
∴,
∵点在反比例函数的图象上,
∴,
故答案为:4.
三、解答题(本大题共有10小题,共86分.)
19. (1)计算:;
(2)解方程:.
【答案】(1)1;(2)
【分析】(1)先根据零指数幂、绝对值的性质、特殊角的三角函数值、负整数指数幂的意义化简,再算加减即可;
(2)两边都乘以化为整式方程求解,然后检验即可.
【详解】解:(1)原式
;
(2),
两边都乘以,得
,
解得,
检验:当时,,
∴原方程的解.
20. (1)解方程:;
(2)解不等式组:
【答案】(1);(2)
【分析】(1)根据配方法解一元二次方程即可求解;
分别求出每一个不等式的解集,根据口诀:
同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】(1)解:,
,
∴,
;
(2)解:,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为:.
为了解某地区九年级学生的视力情况,从该地区九年级学生中抽查了部分学生,
根据调查结果,绘制了如下两幅不完整的统计图.
根据以上信息,解决下列问题:
(1)此次调查的样本容量为 ;
(2)扇形统计图中对应圆心角的度数为 °;
(3)请补全条形统计图;
(4)若该地区九年级学生共有人,请估计其中视力正常的人数.
【答案】(1)450 (2)
(3)见解析 (4)人
【解析】
【分析】(1)根据的人数是人,所占的比例是,据此即可求得此次调查的样本容量;
(2)用类学生数除以,再乘以即可得解;
(3)利用总人数减去、、三类的人数即可求得的人数,从而补全直方图;
(4)利用总人数乘以对应的百分比即可求得.
【小问1详解】
解:,
答:此次调查的样本容量为是,
故答案为.
【小问2详解】
解:,
故答案为;
【小问3详解】
解:
补全图形如下:
【小问4详解】
解:(人)
答:九年级学生共有人,请估计其中视力正常的人数共有人.
甲,乙、丙三人到淮海战役烈士纪念塔园林游览,
若每人分别从纪念塔、纪念馆这两个景点中选择一个参观,且选择每个景点的机会相等,
则三人选择相同景点的概率为多少?
【答案】
【解析】
【分析】根据树状图可进行求解概率.
【详解】解:由题意可得如下树状图:
∴甲、乙、丙三人分别从纪念塔、纪念馆这两个景点中选择一个参观,则共有8种情况,
其中三人选择相同景点参观共有2种,所以三人选择相同景点的概率为.
23. 如图,在菱形中,、分别是、的中点.
求证;
(2) 若菱形的面积为8,则的面积为______.
【答案】(1)见解析
(2)3
【分析】(1) 由四边形ABCD是菱形,即可求得AB=AD,∠B=∠D,又由、分别是、的中点可证得BE=DF,根据SAS,即可证△ABE≌△ADF得AE=AF,从而得证.
(2) 连接AC、BD,交于点O,AC交EF于点G,根据菱形性质可得菱形面积公式,然后根据三角形中位线定理得EF与BD关系,最后根据三角形面积公式代入计算可得答案.
【详解】(1)证明:∵四边形ABCD是菱形,
∴AB=AD,BC=DC,∠B=∠D,
∵、分别是、的中点,
∴,,
∴BE=DF,
在△ABE和△ADF中
,
∴△ABE≌△ADF(SAS);
∴AE=AF,
∴∠AEF=∠AFE.
(2)连接AC、BD,交于点O,AC交EF于点G,
∵四边形ABCD是菱形,
∴AO=OC,菱形ABCD的面积为:,
∵点E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴AC⊥EF,AG=3CG,
设AC=a,BD=b,
∴,即ab=16,
∴.
故答案为:3
24 . 2022年11月,某网店当月售出了“冰墩墩”200个和“雪容融”100个,销售总额为32000元,
12月售出了“冰墩墩”300个和“雪容融”200个,销售总额为52000元.
求“冰墩墩”和“雪容融”的销售单价;
已知“冰墩墩”和“雪容融”的成本分别为102元/个和60元/个.由于冬奥会的举行,
这两款毛绒玩具持续热销,于是该店再次购进这两款毛绒玩具共600个,
其中“雪容融”的数量不超过“冰墩墩”数量的2倍,若购进的这两款毛绒玩具全部售出,
则“冰墩墩”购进多少个时该店当月销售利润最大,并求出最大利润.
【答案】(1)“冰墩墩”和“雪容融”的销售单价分别为120元和80元;
(2)当“冰墩墩”购进200个时该旗舰店当月销售利润最大,最大利润为11600元.
【分析】(1)根据题意,列二元一次方程组即可;
(2)根据题意,列一元一次不等式组,求出m的解集,表示出月销售利润w=-2m+12000,根据函数增减性即可求出最大利润.
【详解】(1)解:设“冰墩墩”和“雪容融”的销售单价分别为x元,y元,
根据题意得,
解得,
答:“冰墩墩”和“雪容融”的销售单价分别为120元和80元;
(2)解:设“冰墩墩”购进m个时该旗舰店当月销售利润最大,此时“雪容融”购进了(600-m)个,
根据题意,得600-m≤2m,
解不等式得m≥200,
设该旗舰店当月销售利润w=(120-102)m+(80-60)(600-m)=-2m+12000,
∵-2<0,
∴w随着m的增大而减小,
∴当m=200时,w最大=-400+12000=11600,
答:当“冰墩墩”购进200个时该旗舰店当月销售利润最大,最大利润为11600元.
25 . 如图,图1是一盏台灯,图2是其侧面示意图(台灯底座高度忽略不计),
其中灯臂,灯罩,灯臂与底座构成的.
可以绕点上下调节一定的角度.使用发现:当与水平线所成的角为时,
台灯光线最佳,求此时点与桌面的距离.(结果精确到,取1.732)
【答案】
【分析】过点作,交延长线于点,过点作于F,过点作于E,
分别在和中,利用锐角三角函数的知识求出和的长,再由矩形的判定和性质得到,最后根据线段的和差计算出的长,问题得解.
【详解】过点作,交延长线于点,过点作于F,过点作于E,
在中,,,
∵
∴(cm),
在中,,,
∵,
∴(cm),
∵,,,
∴四边形是矩形,
∴,
∵,
∴(cm).
答:点与桌面的距离约为.
26 . 如图,在中,,O是上一点,
以为半径的与相切于点D,与相交于点E.
求证:是的平分线;
若,,求的长.
【答案】(1)见解析
(2)6
【分析】(1)根据切线的性质得,再由,得,由平行线的性质得,又因为等腰三角形得,等量代换即可得证;
(2)在中,由勾股定理即可求半径.
【详解】(1)证明:连接OD;
∵与BC相切于点D
∴
∴
∵,
∴
∴
∴
∵
∴
∴
∴是的平分线;
(2)解:∵
∴在中;
∵,
,
设圆的半径为r,
∴
解得,
∴圆的半径为3
∴.
27 . 【发现问题】
如图1,已知和均为等边三角形,在上,在上,
易得线段和的数量关系是______.
将图1中的绕点旋转到图2的位置,直线和直线交于点.
① 判断线段和的数量关系,并证明你的结论;
② 图2中的度数是______.
(3)【探究拓展】
如图3,若和均为等腰直角三角形,,,,
直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
【答案】(1)
(2)①,证明见解析;②;
(3)度,,理由见解析
【分析】(1)由等腰三角形的性质可求解;
(2)①由“SAS”可证,可得;
②由全等三角形的性质可得,即可解决问题.
结论:,.证明,
可得,,由此即可解决问题.
【详解】(1)解:∵和均为等边三角形,
∴,,
∴,
故答案为:;
(2)如图2中,
①∵和均为等边三角形,
∴,,,
∴,
∴(SAS),
∴;
②∵,
∴,
设交于点.
∵,
∴,
∴,
故答案为:;
(3)结论:,.
理由:如图3中,
∵,,,
∴,,
∴,
∴,,
∴,
∵,
∴.
28 . 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,
点P是抛物线上一动点,连接PB,PC.
(1)求抛物线的解析式;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)3;(3)点P的坐标为(1,4)或(﹣2,﹣5)
【分析】(1)用待定系数法求解即可;
(2)先求得点C的坐标,再用待定系数法求得直线BC的解析式;由PE=2ED可得PD=3ED,设P(m,﹣m2+2m+3),则E(m,﹣m+3),用含m的式子表示出PD和DE,根据PD=3ED得出关于m的方程,解得m的值,则可得PE的长,然后按照三角形的面积公式计算即可;
(3)分两种情况:①点C为直角顶点;②点B为直角顶点.过点C作直线P1C⊥BC,交抛物线于点P1,连接P1B,交x轴于点D;过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,分别求得直线P1C和直线BP2的解析式,将它们分别与抛物线的解析式联立,即可求得点P的坐标.
【详解】解:(1)∵抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)在y=﹣x2+2x+3中,当x=0时,y=3,
∴C(0,3).
设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入,得:
,
解得,
∴直线BC的解析式为y=﹣x+3,
若PE=2ED,则PD=3ED,
设P(m,﹣m2+2m+3),
∵PD上x轴于点D,
∴E(m,﹣m+3),
∴﹣m2+2m+3=3(﹣m+3),
∴m2﹣5m+6=0,
解得m1=2,m2=3(舍),
∴m=2,此时P(2,3),E(2,1),
∴PE=2,
∴S△PBC=×2×3=3.
∴△PBC的面积为3;
(3)∵△PBC是以BC为直角边的直角三角形,
∴有两种情况:①点C为直角顶点;②点B为直角顶点.
过点C作直线P1C⊥BC,交抛物线于点P1,连接P1B,交x轴于点D;
过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,如图所示:
∵B(3,0),C(0,3),
∴OB=OC=3,
∴∠BCO=∠OBC=45°.
∵P1C⊥BC,
∴∠DCB=90°,
∴∠DCO=45°,
又∵∠DOC=90°,
∴∠ODC=45°=∠DCO,
∴OD=OC=3,
∴D(﹣3,0),
∴直线P1C的解析式为y=x+3,
联立,
解得或(舍);
∴P1(1,4);
∵P1C⊥BC,BP2⊥BC,
∴P1CBP2,
∴设直线BP2的解析式为y=x+b,
将B(3,0)代入,得0=3+b,
∴b=﹣3,
∴直线BP2的解析式为y=x﹣3,
联立,
解得或(舍),
∴P2(﹣2,﹣5).
综上,点P的坐标为(1,4)或(﹣2,﹣5).
同课章节目录
