人教版数学八年级下册同步练习(含答案版)18.2.1.2 矩形的判定
文档属性
| 名称 | 人教版数学八年级下册同步练习(含答案版)18.2.1.2 矩形的判定 |  | |
| 格式 | docx | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 18:52:13 | ||
图片预览


文档简介
第十八章 平行四边形
18.2.1 矩形
第2课时 矩形的判定
一、选择题
1.在下列条件中,能够判定 ABCD为矩形的是( )
A.AB=AD B.AC⊥BD
C.AB=AC D.∠A=∠B
2.平行四边形的内角平分线能够围成的四边形是( )
A.梯形 B.矩形
C.正方形 D.一般平行四边形
3.如图所示,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
4.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.下列条件中,能判定四边形是矩形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相互平分且相等
6.要判断一个四边形门框是否为矩形,在下面四个策划方案中,正确的方案是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
7.已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DACC.∠BAC=∠ABD D.∠BAC=∠ADB
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
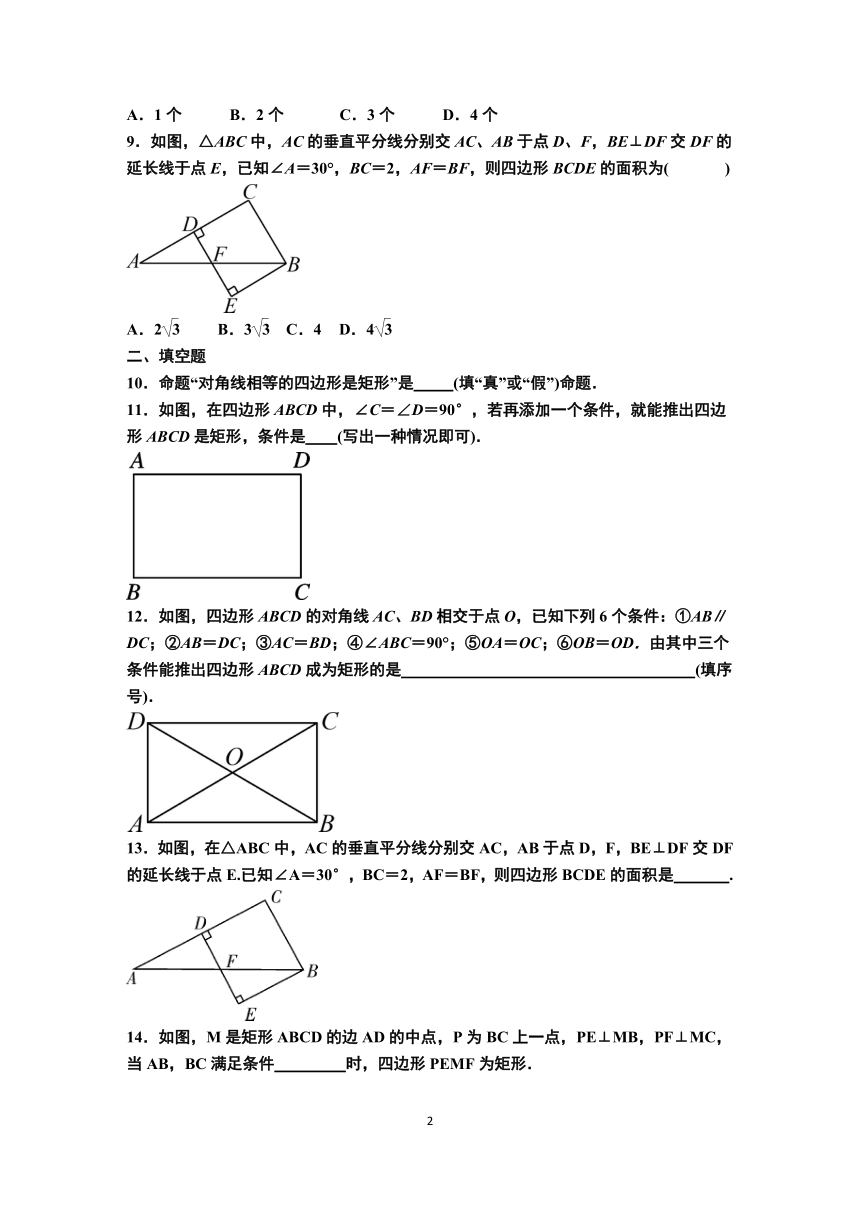
9.如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积为( )
A.2 B.3 C.4 D.4
二、填空题
10.命题“对角线相等的四边形是矩形”是 (填“真”或“假”)命题.
11.如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,条件是 (写出一种情况即可).
12.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.由其中三个条件能推出四边形ABCD成为矩形的是 (填序号).
13.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
14.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件 时,四边形PEMF为矩形.
三、解答题
15.(2023·岳阳中考)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明 ABCD为矩形.
16.如图,BC是等腰△BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
17.如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
(1)求证:四边形ADEC是矩形;
(2)在 ABCD中,取AB的中点M,连接CM,若CM=5,且AC=8,则四边形ADEC的面积为 .
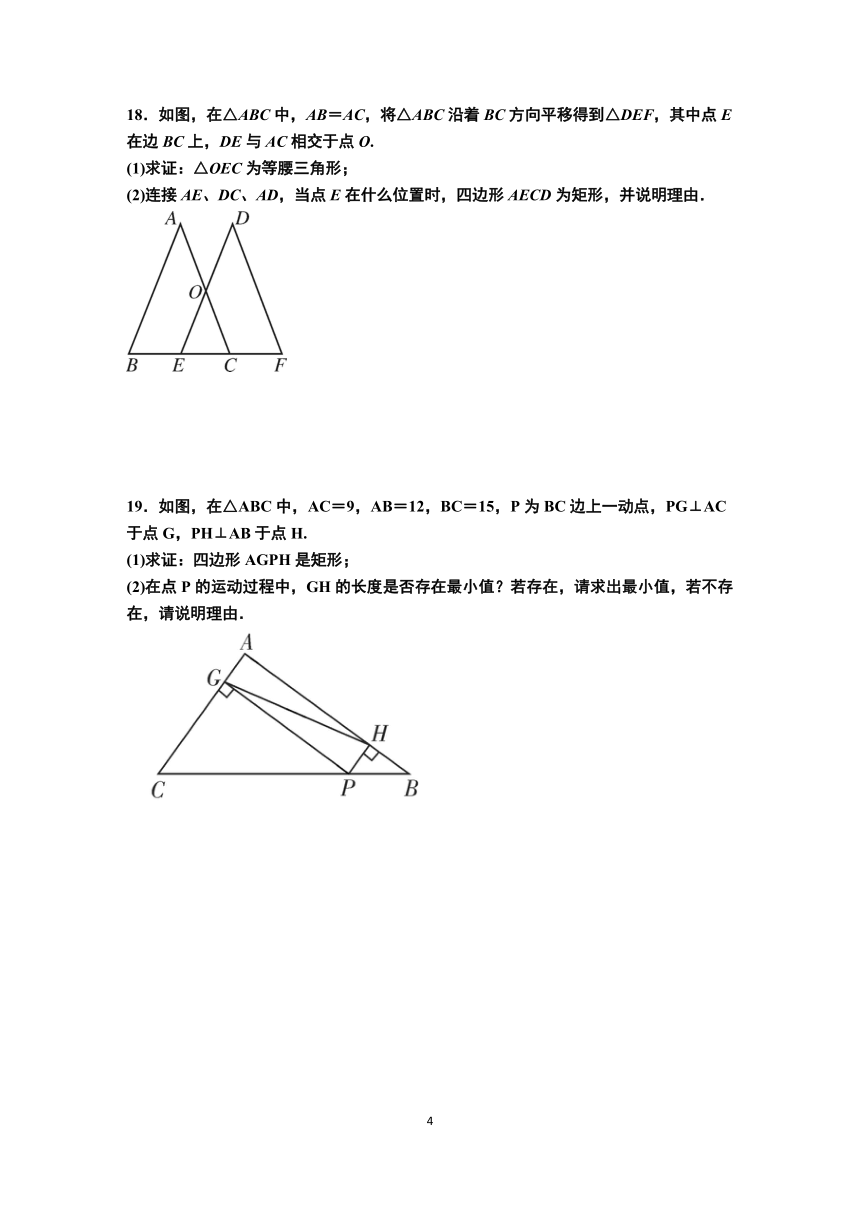
18.如图,在△ABC中,AB=AC,将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
19.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
1
参考答案
一、选择题
1.在下列条件中,能够判定 ABCD为矩形的是( D )
A.AB=AD B.AC⊥BD
C.AB=AC D.∠A=∠B
2.平行四边形的内角平分线能够围成的四边形是( B )
A.梯形 B.矩形
C.正方形 D.一般平行四边形
3.如图所示,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( D )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
4.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.下列条件中,能判定四边形是矩形的是( D )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相互平分且相等
6.要判断一个四边形门框是否为矩形,在下面四个策划方案中,正确的方案是( D )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
7.已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( C )
A.∠BAC=∠DCA B.∠BAC=∠DACC.∠BAC=∠ABD D.∠BAC=∠ADB
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( C )
A.1个 B.2个 C.3个 D.4个
9.如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积为( A )
A.2 B.3 C.4 D.4
二、填空题
10.命题“对角线相等的四边形是矩形”是 (填“真”或“假”)命题.
【答案】假
11.如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,条件是 (写出一种情况即可).
【答案】∠A=90°(答案不唯一)
12.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.由其中三个条件能推出四边形ABCD成为矩形的是 (填序号).
【答案】①②③或①②④或③⑤⑥或④⑤⑥
13.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
【答案】2
14.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件 时,四边形PEMF为矩形.
【答案】BC=2AB
三、解答题
15.(2023·岳阳中考)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明 ABCD为矩形.
【答案】(1)①(或②)
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
在△ABM和△DCM中,
∴△ABM≌△DCM(SAS).
∴∠A=∠D.∴∠A=∠D=90°.
∴ ABCD为矩形.(选②证明也可以)
16.如图,BC是等腰△BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
解:四边形ABCD是矩形,
理由:∵BC是等腰△BED底边ED上的高,∴EC=CD.
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE.
∴四边形ABCD是平行四边形.
∵AC=BE,BE=BD,∴AC=BD,
∴四边形ABCD是矩形.
17.如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
(1)求证:四边形ADEC是矩形;
(2)在 ABCD中,取AB的中点M,连接CM,若CM=5,且AC=8,则四边形ADEC的面积为 .
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.∵DE∥AC,
∴四边形ADEC是平行四边形.又∵AC⊥BC,∴∠ACE=90°.
∴四边形ADEC是矩形.
(2)48
18.如图,在△ABC中,AB=AC,将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵△ABC平移得到△DEF,∴AB∥DE,∴∠ABC=∠DEF,∴∠DEF=∠ACB,即△OEC为等腰三角形;
(2)解:当E为BC中点时,四边形AECD为矩形,∵AB=AC,且E为BC中点,∴AE⊥BC,BE=EC,∵△ABC平移得到△DEF,∴BE∥AD,BE=AD,∴AD∥EC,AD=EC,∴四边形AECD为平行四边形,又∵AE⊥BC,∴四边形AECD为矩形
19.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
(1)证明:∵AC=9,
AB=12,BC=15,
∴AC2+AB2=BC2.
∴∠A=90°.
∵PG⊥AC,PH⊥AB,∴∠AGP=∠AHP=90°.
∴四边形AGPH是矩形.
(2)解:存在.连接AP.∵四边形AGPH是矩形,∴GH=AP.当AP⊥BC时,AP最短.
∵S△ABC=AC·AB=BC·AP,
∴9×12=15·AP.∴AP=.
∴GH的最小值为.
18.2.1 矩形
第2课时 矩形的判定
一、选择题
1.在下列条件中,能够判定 ABCD为矩形的是( )
A.AB=AD B.AC⊥BD
C.AB=AC D.∠A=∠B
2.平行四边形的内角平分线能够围成的四边形是( )
A.梯形 B.矩形
C.正方形 D.一般平行四边形
3.如图所示,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
4.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.下列条件中,能判定四边形是矩形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相互平分且相等
6.要判断一个四边形门框是否为矩形,在下面四个策划方案中,正确的方案是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
7.已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )
A.∠BAC=∠DCA B.∠BAC=∠DACC.∠BAC=∠ABD D.∠BAC=∠ADB
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( )
A.1个 B.2个 C.3个 D.4个
9.如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积为( )
A.2 B.3 C.4 D.4
二、填空题
10.命题“对角线相等的四边形是矩形”是 (填“真”或“假”)命题.
11.如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,条件是 (写出一种情况即可).
12.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.由其中三个条件能推出四边形ABCD成为矩形的是 (填序号).
13.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
14.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件 时,四边形PEMF为矩形.
三、解答题
15.(2023·岳阳中考)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明 ABCD为矩形.
16.如图,BC是等腰△BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
17.如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
(1)求证:四边形ADEC是矩形;
(2)在 ABCD中,取AB的中点M,连接CM,若CM=5,且AC=8,则四边形ADEC的面积为 .
18.如图,在△ABC中,AB=AC,将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
19.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
1
参考答案
一、选择题
1.在下列条件中,能够判定 ABCD为矩形的是( D )
A.AB=AD B.AC⊥BD
C.AB=AC D.∠A=∠B
2.平行四边形的内角平分线能够围成的四边形是( B )
A.梯形 B.矩形
C.正方形 D.一般平行四边形
3.如图所示,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( D )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
4.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分 D.矩形的对角线相等且互相平分
5.下列条件中,能判定四边形是矩形的是( D )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相互平分且相等
6.要判断一个四边形门框是否为矩形,在下面四个策划方案中,正确的方案是( D )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
7.已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( C )
A.∠BAC=∠DCA B.∠BAC=∠DACC.∠BAC=∠ABD D.∠BAC=∠ADB
8.如图,在 ABCD中,对角线AC与BD相交于点O,对于下列条件:①∠1+∠3=90°;②BC2+CD2=AC2;③∠1=∠2;④AC⊥BD.能判定四边形ABCD是矩形的个数是( C )
A.1个 B.2个 C.3个 D.4个
9.如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积为( A )
A.2 B.3 C.4 D.4
二、填空题
10.命题“对角线相等的四边形是矩形”是 (填“真”或“假”)命题.
【答案】假
11.如图,在四边形ABCD中,∠C=∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,条件是 (写出一种情况即可).
【答案】∠A=90°(答案不唯一)
12.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.由其中三个条件能推出四边形ABCD成为矩形的是 (填序号).
【答案】①②③或①②④或③⑤⑥或④⑤⑥
13.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E.已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 .
【答案】2
14.如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MB,PF⊥MC,当AB,BC满足条件 时,四边形PEMF为矩形.
【答案】BC=2AB
三、解答题
15.(2023·岳阳中考)如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是 (填序号);
(2)添加条件后,请证明 ABCD为矩形.
【答案】(1)①(或②)
(2)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
在△ABM和△DCM中,
∴△ABM≌△DCM(SAS).
∴∠A=∠D.∴∠A=∠D=90°.
∴ ABCD为矩形.(选②证明也可以)
16.如图,BC是等腰△BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
解:四边形ABCD是矩形,
理由:∵BC是等腰△BED底边ED上的高,∴EC=CD.
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE.
∴四边形ABCD是平行四边形.
∵AC=BE,BE=BD,∴AC=BD,
∴四边形ABCD是矩形.
17.如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
(1)求证:四边形ADEC是矩形;
(2)在 ABCD中,取AB的中点M,连接CM,若CM=5,且AC=8,则四边形ADEC的面积为 .
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.∵DE∥AC,
∴四边形ADEC是平行四边形.又∵AC⊥BC,∴∠ACE=90°.
∴四边形ADEC是矩形.
(2)48
18.如图,在△ABC中,AB=AC,将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
(1)证明:∵AB=AC,∴∠ABC=∠ACB,∵△ABC平移得到△DEF,∴AB∥DE,∴∠ABC=∠DEF,∴∠DEF=∠ACB,即△OEC为等腰三角形;
(2)解:当E为BC中点时,四边形AECD为矩形,∵AB=AC,且E为BC中点,∴AE⊥BC,BE=EC,∵△ABC平移得到△DEF,∴BE∥AD,BE=AD,∴AD∥EC,AD=EC,∴四边形AECD为平行四边形,又∵AE⊥BC,∴四边形AECD为矩形
19.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
(1)证明:∵AC=9,
AB=12,BC=15,
∴AC2+AB2=BC2.
∴∠A=90°.
∵PG⊥AC,PH⊥AB,∴∠AGP=∠AHP=90°.
∴四边形AGPH是矩形.
(2)解:存在.连接AP.∵四边形AGPH是矩形,∴GH=AP.当AP⊥BC时,AP最短.
∵S△ABC=AC·AB=BC·AP,
∴9×12=15·AP.∴AP=.
∴GH的最小值为.
