2023-2024学人教版七年级数学下册第五章 相交线与平行线 单元练习(含答案)
文档属性
| 名称 | 2023-2024学人教版七年级数学下册第五章 相交线与平行线 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 307.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 20:15:54 | ||
图片预览



文档简介
第五章 相交线与平行线 单元练习
一.选择题(共12小题)
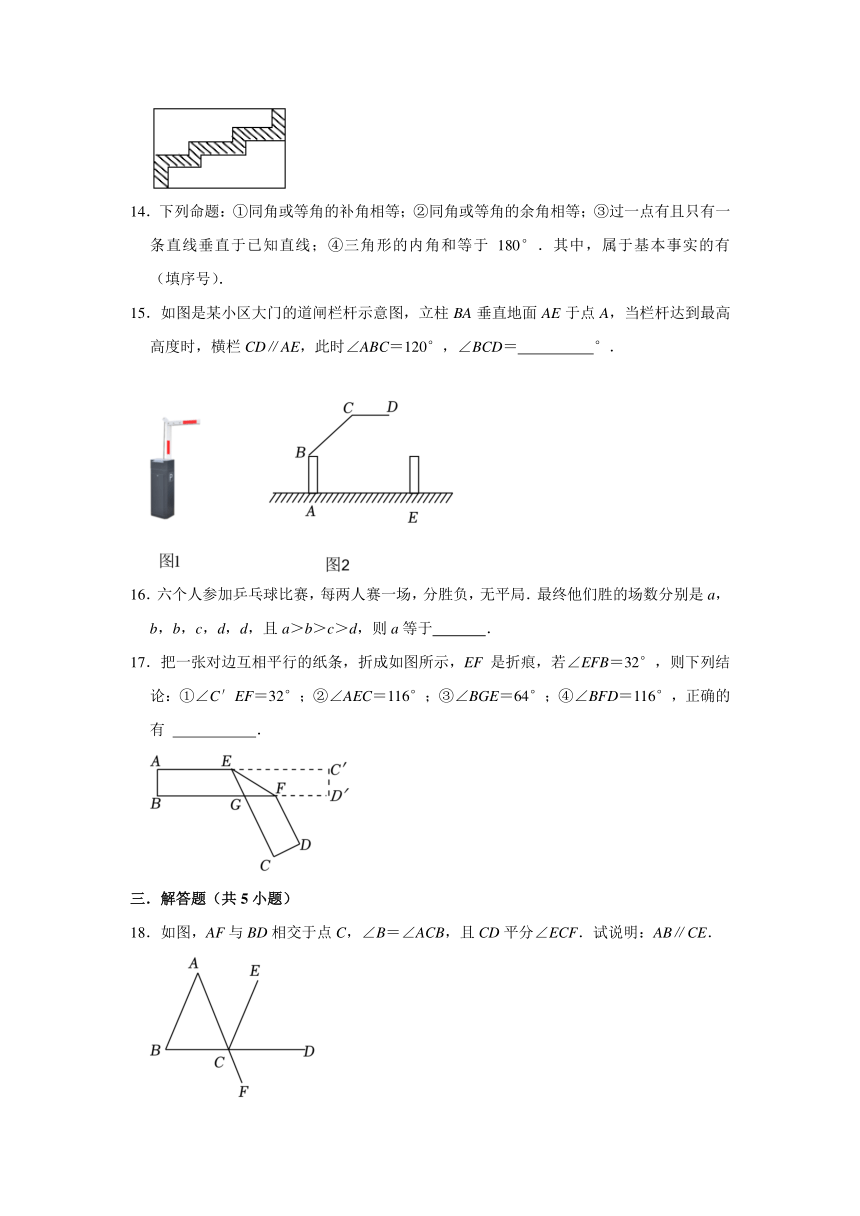
1.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
2.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
3.如图,添加下列一个条件后,能判定AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠B+∠D=180° D.∠1+∠3+∠D=180°
4.如图,∠1和∠4的位置关系是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
5.下列现象是数学中的平移的是( )
A.树叶从树上落下
B.电梯从底楼升到顶楼
C.骑自行车时轮胎的滚动
D.钟摆的摆动
6.如图,下列条件中,不能判断AD∥BE的是( )
A.∠1=∠4 B.∠B=∠5
C.∠D=∠5 D.∠BAD+∠B=180°
7.如图,将△ABC沿直线AB向右平移2cm后到达△BDE的位置,若△ABC的周长为11cm,则四边形ADEC的周长为( )
A.13cm B.15cm C.16cm D.17cm
8.如图,AB∥CD,BE∥DF,∠DBE的平分线与∠CDF的平分线交于点G,当∠BGD=65°时,∠BDC=( )
A.65° B.60° C.55° D.50°
9.如图,点D在直线AB上,CD⊥ED,则图中的∠1和∠2的关系是( )
A.互为补角 B.对顶角 C.同位角 D.互为余角
10.如图,正方形ABCD中,EF≠AB,点P、Q、R、S分别是AB,BC,CD,DA上的点,有以下四个命题:
①若SQ∥EF,则SQ=EF;
②若SQ=EF,则SQ∥EF;
③若PR⊥EF,则PR=EF;
④若PR=EF,则PR⊥EF.其中真命题有( )
A.①② B.③④ C.①③ D.①②③④
11.小宇设计了一个随机碰撞模拟器:在模拟器中有A,B,C三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个C型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个A型小球和一个C型小球发生碰撞,会变成一个B型小球.现在模拟器中有A型小球12个,B型小球9个,C型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:其中正确的说法是( )
①最后剩下的小球可能是A型小球;
②最后剩下的小球一定是B型小球;
③最后剩下的小球一定不是C型小球.
A.① B.②③ C.③ D.①③
12.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:①∠D=30°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,在一块长为20m,宽为14m的草地上有一条宽为2m的曲折小路,运用你所学的知识求出这块草地的绿地面积为 m2.
14.下列命题:①同角或等角的补角相等;②同角或等角的余角相等;③过一点有且只有一条直线垂直于已知直线;④三角形的内角和等于180°.其中,属于基本事实的有 (填序号).
15.如图是某小区大门的道闸栏杆示意图,立柱BA垂直地面AE于点A,当栏杆达到最高高度时,横栏CD∥AE,此时∠ABC=120°,∠BCD= °.
16.六个人参加乒乓球比赛,每两人赛一场,分胜负,无平局.最终他们胜的场数分别是a,b,b,c,d,d,且a>b>c>d,则a等于 .
17.把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论:①∠C′EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°,正确的有 .
三.解答题(共5小题)
18.如图,AF与BD相交于点C,∠B=∠ACB,且CD平分∠ECF.试说明:AB∥CE.
19.如图,直线MN与直线AB,CD分别交于点E,F,∠1与∠2互补.
(1)如图1,求证AB∥CD;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP的延长线与CD交于点G,点H是MN上一点,且PF∥GH,求证:GH⊥EG;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,交MN于点Q,∠QPF:∠HPK=3:2,求∠HPF的度数.
20.如图,EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
21.如图,∠A=59°,∠D=121°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)求∠DFE的度数;
(2)若∠BFP=48°,请判断CE与PF是否平行.
22.(1)如图①,MA1∥NA2,则∠A1+∠A2= ;如图②,MA1∥NA3,则∠A1+∠A2+∠A3= ;
(2)如图③,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4= ;
(3)利用上述结论解决问题:如图④,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=80°,求∠BFD的度数.
参考答案
一.选择题(共12小题)
1--10ABDBB BBDDC 11--12DB
二.填空题(共5小题)
13.216
14.③
15.150
16.4
17.①②③④
三.解答题(共5小题)
18.证明:因为CD平分∠ECF,
所以∠ECD=∠FCD(角平分线的定义).
因为∠ACB=∠FCD(对顶角相等),
所以∠ECD=∠ACB(等量代换).
因为∠B=∠ACB,
所以∠B=∠ECD(等量代换).
所以AB∥CE(同位角相等,两直线平行).
19.(1)证明:由题意可得:∠1+∠2=180°,∠1+∠BEF=180°,
∴∠2=∠BEF,
∴AB∥CD,
(2)证明:由题意可得:EP平分∠BEF,FP平分∠EFD,
∴,
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴,
∴∠EPF=90°,
∵PF∥GH,
∴∠PGH=90°,即GH⊥EG;
(3)解设∠HPK=2x°,则∠QPF=3x°,∠PHK=∠HPK=2x°,
∵PF∥GH,
∴∠PHK=∠FPH=2x°,
∴∠QPK=7x°,
又∵PQ平分∠EPK,
∴∠EPQ=∠QPK=7x°,
由(2)得:∠EPF=∠EPQ+∠QPF=90°,即3x°+7x°=90°,
解得x=9,
∴∠HPF=18°.
20.(1)证明:∵EF∥CD,
∴∠1+∠4=180°,
又∵∠1+∠2=180°,
∴∠2=∠4,
∴GD∥CA;
(2)解:∵GD∥CA,∠A=40°,
∴∠3=∠A=40°,∠4=∠2,
∵DG平分∠CDB,
∴∠2=∠3=40°,
∴∠4=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠4=80°.
21.解:(1)∵∠A=59°,∠D=121°,
∴∠A+∠D=180°,
∴AB∥CD,
∴∠DFE=∠1,
∵∠1=3∠2,∠2=24°,
∴∠DFE=72°;
(2)CE∥PF,
理由:∵∠DFE=72°,
∴∠BFC=72°,
∵∠BFP=48°,
∴∠PFC=72°﹣48°=24°,
∵∠2=24°,
∴∠PFC=∠2,
∴CE∥PF.
22.解:(1)如图①,根据MA1∥NA2,可得∠A1+∠A2=180°,
如图②,过A2作PA2∥MA1,
∵MA1∥NA3,
∴PA2∥MA1∥NA3,
∴∠A1+∠A1A2P=180°,∠A3+∠A3A2P=180°,
∴∠A1+∠A1A2A3+∠A3=360°;
故答案为:180°,360°;
(2)如图③,过A2作PA2∥MA1,过A3作QA3∥MA1,
∵MA1∥NA3,
∴QA3∥PA2∥MA1∥NA3,
∴∠A1+∠A1A2P=180°,∠QA3A2+∠A3A2P=180°,∠A4+∠A4A3Q=180°,
∴∠A1+∠A2+∠A3+∠A4=540°;
故答案为:540°;
(3)如图④,过F作FG∥AB,则AB∥CD∥FG,
∴∠BFG=∠ABF,∠GFD=∠CDF,
∵∠ABE和∠CDE的平分线相交于点F,
∴∠BFD=(∠ABE+∠CDE),
又∵∠ABE+∠E+∠CDE=360°,∠E=80°,
∴∠ABE+∠CDE=280°,
∴∠BFD=140
一.选择题(共12小题)
1.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
2.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
3.如图,添加下列一个条件后,能判定AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠B+∠D=180° D.∠1+∠3+∠D=180°
4.如图,∠1和∠4的位置关系是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
5.下列现象是数学中的平移的是( )
A.树叶从树上落下
B.电梯从底楼升到顶楼
C.骑自行车时轮胎的滚动
D.钟摆的摆动
6.如图,下列条件中,不能判断AD∥BE的是( )
A.∠1=∠4 B.∠B=∠5
C.∠D=∠5 D.∠BAD+∠B=180°
7.如图,将△ABC沿直线AB向右平移2cm后到达△BDE的位置,若△ABC的周长为11cm,则四边形ADEC的周长为( )
A.13cm B.15cm C.16cm D.17cm
8.如图,AB∥CD,BE∥DF,∠DBE的平分线与∠CDF的平分线交于点G,当∠BGD=65°时,∠BDC=( )
A.65° B.60° C.55° D.50°
9.如图,点D在直线AB上,CD⊥ED,则图中的∠1和∠2的关系是( )
A.互为补角 B.对顶角 C.同位角 D.互为余角
10.如图,正方形ABCD中,EF≠AB,点P、Q、R、S分别是AB,BC,CD,DA上的点,有以下四个命题:
①若SQ∥EF,则SQ=EF;
②若SQ=EF,则SQ∥EF;
③若PR⊥EF,则PR=EF;
④若PR=EF,则PR⊥EF.其中真命题有( )
A.①② B.③④ C.①③ D.①②③④
11.小宇设计了一个随机碰撞模拟器:在模拟器中有A,B,C三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个C型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个A型小球和一个C型小球发生碰撞,会变成一个B型小球.现在模拟器中有A型小球12个,B型小球9个,C型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:其中正确的说法是( )
①最后剩下的小球可能是A型小球;
②最后剩下的小球一定是B型小球;
③最后剩下的小球一定不是C型小球.
A.① B.②③ C.③ D.①③
12.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:①∠D=30°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,在一块长为20m,宽为14m的草地上有一条宽为2m的曲折小路,运用你所学的知识求出这块草地的绿地面积为 m2.
14.下列命题:①同角或等角的补角相等;②同角或等角的余角相等;③过一点有且只有一条直线垂直于已知直线;④三角形的内角和等于180°.其中,属于基本事实的有 (填序号).
15.如图是某小区大门的道闸栏杆示意图,立柱BA垂直地面AE于点A,当栏杆达到最高高度时,横栏CD∥AE,此时∠ABC=120°,∠BCD= °.
16.六个人参加乒乓球比赛,每两人赛一场,分胜负,无平局.最终他们胜的场数分别是a,b,b,c,d,d,且a>b>c>d,则a等于 .
17.把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论:①∠C′EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°,正确的有 .
三.解答题(共5小题)
18.如图,AF与BD相交于点C,∠B=∠ACB,且CD平分∠ECF.试说明:AB∥CE.
19.如图,直线MN与直线AB,CD分别交于点E,F,∠1与∠2互补.
(1)如图1,求证AB∥CD;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP的延长线与CD交于点G,点H是MN上一点,且PF∥GH,求证:GH⊥EG;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,交MN于点Q,∠QPF:∠HPK=3:2,求∠HPF的度数.
20.如图,EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
21.如图,∠A=59°,∠D=121°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)求∠DFE的度数;
(2)若∠BFP=48°,请判断CE与PF是否平行.
22.(1)如图①,MA1∥NA2,则∠A1+∠A2= ;如图②,MA1∥NA3,则∠A1+∠A2+∠A3= ;
(2)如图③,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4= ;
(3)利用上述结论解决问题:如图④,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=80°,求∠BFD的度数.
参考答案
一.选择题(共12小题)
1--10ABDBB BBDDC 11--12DB
二.填空题(共5小题)
13.216
14.③
15.150
16.4
17.①②③④
三.解答题(共5小题)
18.证明:因为CD平分∠ECF,
所以∠ECD=∠FCD(角平分线的定义).
因为∠ACB=∠FCD(对顶角相等),
所以∠ECD=∠ACB(等量代换).
因为∠B=∠ACB,
所以∠B=∠ECD(等量代换).
所以AB∥CE(同位角相等,两直线平行).
19.(1)证明:由题意可得:∠1+∠2=180°,∠1+∠BEF=180°,
∴∠2=∠BEF,
∴AB∥CD,
(2)证明:由题意可得:EP平分∠BEF,FP平分∠EFD,
∴,
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴,
∴∠EPF=90°,
∵PF∥GH,
∴∠PGH=90°,即GH⊥EG;
(3)解设∠HPK=2x°,则∠QPF=3x°,∠PHK=∠HPK=2x°,
∵PF∥GH,
∴∠PHK=∠FPH=2x°,
∴∠QPK=7x°,
又∵PQ平分∠EPK,
∴∠EPQ=∠QPK=7x°,
由(2)得:∠EPF=∠EPQ+∠QPF=90°,即3x°+7x°=90°,
解得x=9,
∴∠HPF=18°.
20.(1)证明:∵EF∥CD,
∴∠1+∠4=180°,
又∵∠1+∠2=180°,
∴∠2=∠4,
∴GD∥CA;
(2)解:∵GD∥CA,∠A=40°,
∴∠3=∠A=40°,∠4=∠2,
∵DG平分∠CDB,
∴∠2=∠3=40°,
∴∠4=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠4=80°.
21.解:(1)∵∠A=59°,∠D=121°,
∴∠A+∠D=180°,
∴AB∥CD,
∴∠DFE=∠1,
∵∠1=3∠2,∠2=24°,
∴∠DFE=72°;
(2)CE∥PF,
理由:∵∠DFE=72°,
∴∠BFC=72°,
∵∠BFP=48°,
∴∠PFC=72°﹣48°=24°,
∵∠2=24°,
∴∠PFC=∠2,
∴CE∥PF.
22.解:(1)如图①,根据MA1∥NA2,可得∠A1+∠A2=180°,
如图②,过A2作PA2∥MA1,
∵MA1∥NA3,
∴PA2∥MA1∥NA3,
∴∠A1+∠A1A2P=180°,∠A3+∠A3A2P=180°,
∴∠A1+∠A1A2A3+∠A3=360°;
故答案为:180°,360°;
(2)如图③,过A2作PA2∥MA1,过A3作QA3∥MA1,
∵MA1∥NA3,
∴QA3∥PA2∥MA1∥NA3,
∴∠A1+∠A1A2P=180°,∠QA3A2+∠A3A2P=180°,∠A4+∠A4A3Q=180°,
∴∠A1+∠A2+∠A3+∠A4=540°;
故答案为:540°;
(3)如图④,过F作FG∥AB,则AB∥CD∥FG,
∴∠BFG=∠ABF,∠GFD=∠CDF,
∵∠ABE和∠CDE的平分线相交于点F,
∴∠BFD=(∠ABE+∠CDE),
又∵∠ABE+∠E+∠CDE=360°,∠E=80°,
∴∠ABE+∠CDE=280°,
∴∠BFD=140
