18.1.2 平行四边形的判定同步练习(含解析)
文档属性
| 名称 | 18.1.2 平行四边形的判定同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.1.2 平行四边形的判定
一、单选题
1.如图, 、 两处被池塘隔开,为了测量 、 两处的距离,在 外选一点 ,连接 、 ,并分别取线段 、 的中点 、 ,测得 ,则 的长为( )
A. B. C. D.
2.如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE,则他只需测量( )
A.AD长 B.AE长 C.DE长 D.AC长
3.在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
二、填空题
4.四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需满足的条件 (横线只需填一个你认为合适的条件即可)
5. M、N分别是△ABC中AB、AC的中点,若BC=6,则MN= .
6.三角形的三条中位线的长分别是3,4,5,则这个三角形的周长是 .
三、综合题
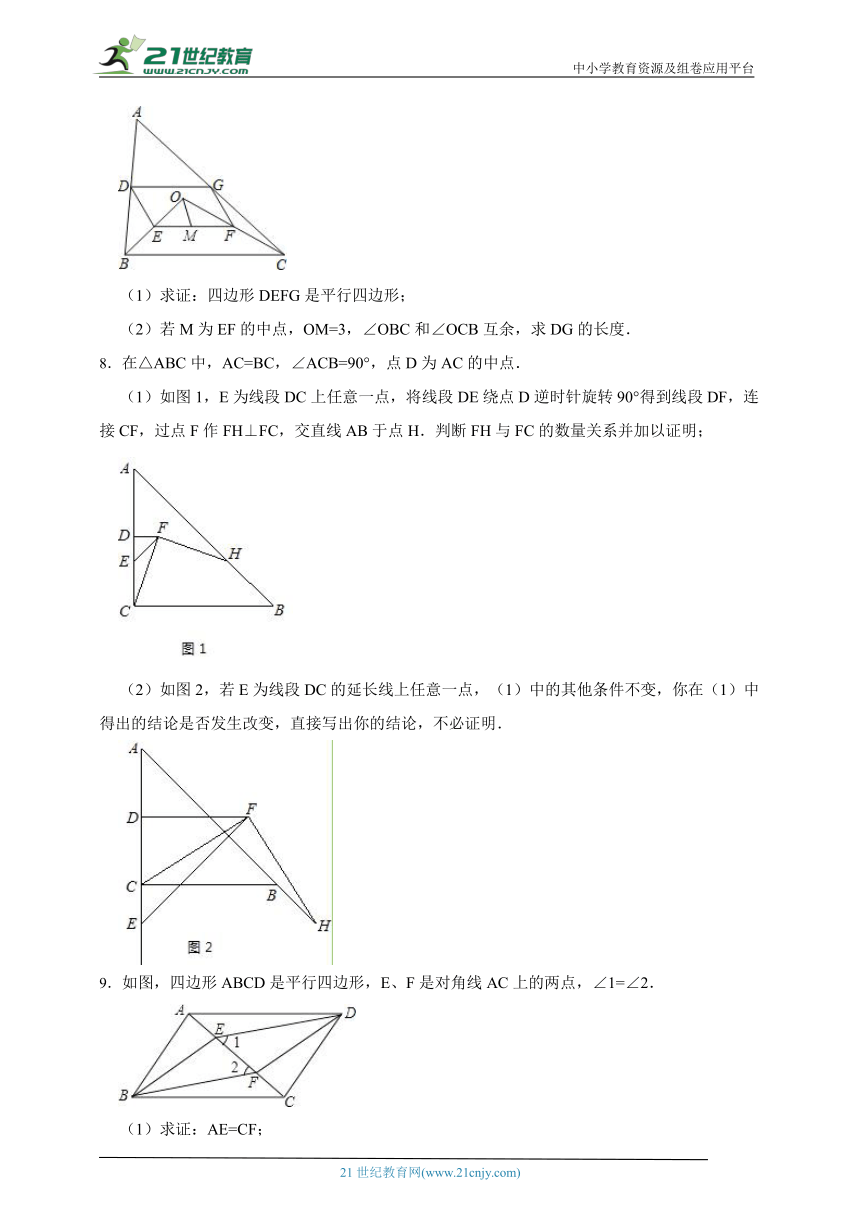
7.如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
8.在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
9.如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
答案解析部分
1.【答案】C
【解析】【解答】解: 、 是 、 的中点,
是 的中位线,
,
,
.
故答案为: .
【分析】根据题意直接利用三角形中位线等于第三边的一半可求出 .
2.【答案】C
【解析】【解答】解:∵D、E是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∴ 他只需测量DE的长;
故答案为:C.
【分析】三角形的中位线平行第三边,且等于第三边的一半,据此解答即可.
3.【答案】D
【解析】【解答】A、根据两组对边分别平行的四边形为平行四边形;A不符合题意;
B、根据两组对边分别相等的四边形为平行四边形;B不符合题意;
C、根据对角线互相平分的四边形是平行四边形;C不符合题意;
D、不能判定.D符合题意.
【分析】本题让找错误的判定定理,D中一组对边平行,另一组对边相等,不等判定四边形为平行四边形.
4.【答案】AD ="BC" (或AD ∥BC等)
【解析】【解答】解:根据平行四边形的判定方法,需要增加的条件是:AD=BC或AB∥CD或∠A=∠C或∠B=∠D.故答案为:AD=BC(或AB∥CD).
【分析】根据一组对边平行且相等的四边形是平行四边形可添加AD=BC;
根据两组对边分别平行的四边形是平行四边形可添加AB∥CD。(答案不唯一)
5.【答案】3
【解析】【解答】解:∵△ABC中,M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∵BC=6,
∴MN=BC=3,
故答案为:3.
【分析】三角形的中位线平行于第三边且等于第三边的一半,据此解答即可.
6.【答案】24
【解析】【解答】解:∵三角形的三条中位线的长分别是3,4,5,
∴三角形的三条边的长分别是6,8,10,
∴这个三角形的周长=6+8+10=24.
故答案为:24.
【分析】三角形的中位线等于第三边的一半,由此可得三角形的三条边的长分别是6,8,10,据此可得三角形的周长.
7.【答案】(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG= BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF= BC,
∴DE=EF,DG∥EF,
∴四边形DEFG是平行四边形。
(2)解:∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
【解析】【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF= BC,DG∥BC且DG= BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.此题是平行四边形的判定与性质题,主要考查了平行四边形的判定和性质,三角形的中位线,直角三角形的性质,解本题的关键是判定四边形DEFG是平行四边形.
8.【答案】(1)解:FH与FC的数量关系是:FH=FC.
证明如下:延长DF交AB于点G,
由题意,知∠EDF=∠ACB=90°,DE=DF,
∴DG∥CB,
∵点D为AC的中点,
∴点G为AB的中点,且 ,
∴DG为△ABC的中位线,
∴ .
∵AC=BC,
∴DC=DG,
∴DC﹣DE=DG﹣DF,
即EC=FG.
∵∠EDF=90°,FH⊥FC,
∴∠1+∠CFD=90°,∠2+∠CFD=90°,
∴∠1=∠2.
∵△DEF与△ADG都是等腰直角三角形,
∴∠DEF=∠DGA=45°,
∴∠CEF=∠FGH=135°,
∴△CEF≌△FGH,
∴CF=FH
(2)解:FH与FC仍然相等.
理由:由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG= BC,DC= AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中
,
∴△FCE≌△HFG(ASA),
∴HF=FC
【解析】【分析】(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠1=∠2=90°﹣∠DFC,∠CEF=∠FGH=135°,由AAS证出△CEF≌△FGH.∴CF=FH.(2)通过证明△CEF≌△FGH(ASA)得出.
9.【答案】(1)证明:如图:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2
∴∠5=∠6
∵在△ADE与△CBF中,
∴△ADE≌△CBF(ASA),
∴AE=CF
(2)证明:∵∠1=∠2,
∴DE∥BF.
又∵由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
【解析】【分析】(1)通过全等三角形△ADE≌△CBF的对应边相等证得AE=CF;(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
18.1.2 平行四边形的判定
一、单选题
1.如图, 、 两处被池塘隔开,为了测量 、 两处的距离,在 外选一点 ,连接 、 ,并分别取线段 、 的中点 、 ,测得 ,则 的长为( )
A. B. C. D.
2.如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE,则他只需测量( )
A.AD长 B.AE长 C.DE长 D.AC长
3.在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
二、填空题
4.四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需满足的条件 (横线只需填一个你认为合适的条件即可)
5. M、N分别是△ABC中AB、AC的中点,若BC=6,则MN= .
6.三角形的三条中位线的长分别是3,4,5,则这个三角形的周长是 .
三、综合题
7.如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
8.在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
9.如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
答案解析部分
1.【答案】C
【解析】【解答】解: 、 是 、 的中点,
是 的中位线,
,
,
.
故答案为: .
【分析】根据题意直接利用三角形中位线等于第三边的一半可求出 .
2.【答案】C
【解析】【解答】解:∵D、E是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∴ 他只需测量DE的长;
故答案为:C.
【分析】三角形的中位线平行第三边,且等于第三边的一半,据此解答即可.
3.【答案】D
【解析】【解答】A、根据两组对边分别平行的四边形为平行四边形;A不符合题意;
B、根据两组对边分别相等的四边形为平行四边形;B不符合题意;
C、根据对角线互相平分的四边形是平行四边形;C不符合题意;
D、不能判定.D符合题意.
【分析】本题让找错误的判定定理,D中一组对边平行,另一组对边相等,不等判定四边形为平行四边形.
4.【答案】AD ="BC" (或AD ∥BC等)
【解析】【解答】解:根据平行四边形的判定方法,需要增加的条件是:AD=BC或AB∥CD或∠A=∠C或∠B=∠D.故答案为:AD=BC(或AB∥CD).
【分析】根据一组对边平行且相等的四边形是平行四边形可添加AD=BC;
根据两组对边分别平行的四边形是平行四边形可添加AB∥CD。(答案不唯一)
5.【答案】3
【解析】【解答】解:∵△ABC中,M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∵BC=6,
∴MN=BC=3,
故答案为:3.
【分析】三角形的中位线平行于第三边且等于第三边的一半,据此解答即可.
6.【答案】24
【解析】【解答】解:∵三角形的三条中位线的长分别是3,4,5,
∴三角形的三条边的长分别是6,8,10,
∴这个三角形的周长=6+8+10=24.
故答案为:24.
【分析】三角形的中位线等于第三边的一半,由此可得三角形的三条边的长分别是6,8,10,据此可得三角形的周长.
7.【答案】(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG= BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF= BC,
∴DE=EF,DG∥EF,
∴四边形DEFG是平行四边形。
(2)解:∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6.
【解析】【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF= BC,DG∥BC且DG= BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.此题是平行四边形的判定与性质题,主要考查了平行四边形的判定和性质,三角形的中位线,直角三角形的性质,解本题的关键是判定四边形DEFG是平行四边形.
8.【答案】(1)解:FH与FC的数量关系是:FH=FC.
证明如下:延长DF交AB于点G,
由题意,知∠EDF=∠ACB=90°,DE=DF,
∴DG∥CB,
∵点D为AC的中点,
∴点G为AB的中点,且 ,
∴DG为△ABC的中位线,
∴ .
∵AC=BC,
∴DC=DG,
∴DC﹣DE=DG﹣DF,
即EC=FG.
∵∠EDF=90°,FH⊥FC,
∴∠1+∠CFD=90°,∠2+∠CFD=90°,
∴∠1=∠2.
∵△DEF与△ADG都是等腰直角三角形,
∴∠DEF=∠DGA=45°,
∴∠CEF=∠FGH=135°,
∴△CEF≌△FGH,
∴CF=FH
(2)解:FH与FC仍然相等.
理由:由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG= BC,DC= AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中
,
∴△FCE≌△HFG(ASA),
∴HF=FC
【解析】【分析】(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠1=∠2=90°﹣∠DFC,∠CEF=∠FGH=135°,由AAS证出△CEF≌△FGH.∴CF=FH.(2)通过证明△CEF≌△FGH(ASA)得出.
9.【答案】(1)证明:如图:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2
∴∠5=∠6
∵在△ADE与△CBF中,
∴△ADE≌△CBF(ASA),
∴AE=CF
(2)证明:∵∠1=∠2,
∴DE∥BF.
又∵由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
【解析】【分析】(1)通过全等三角形△ADE≌△CBF的对应边相等证得AE=CF;(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
