北师大版数学七年级下册第2章第1节两条直线的位置关系同步练习(附详细分析)
文档属性
| 名称 | 北师大版数学七年级下册第2章第1节两条直线的位置关系同步练习(附详细分析) | 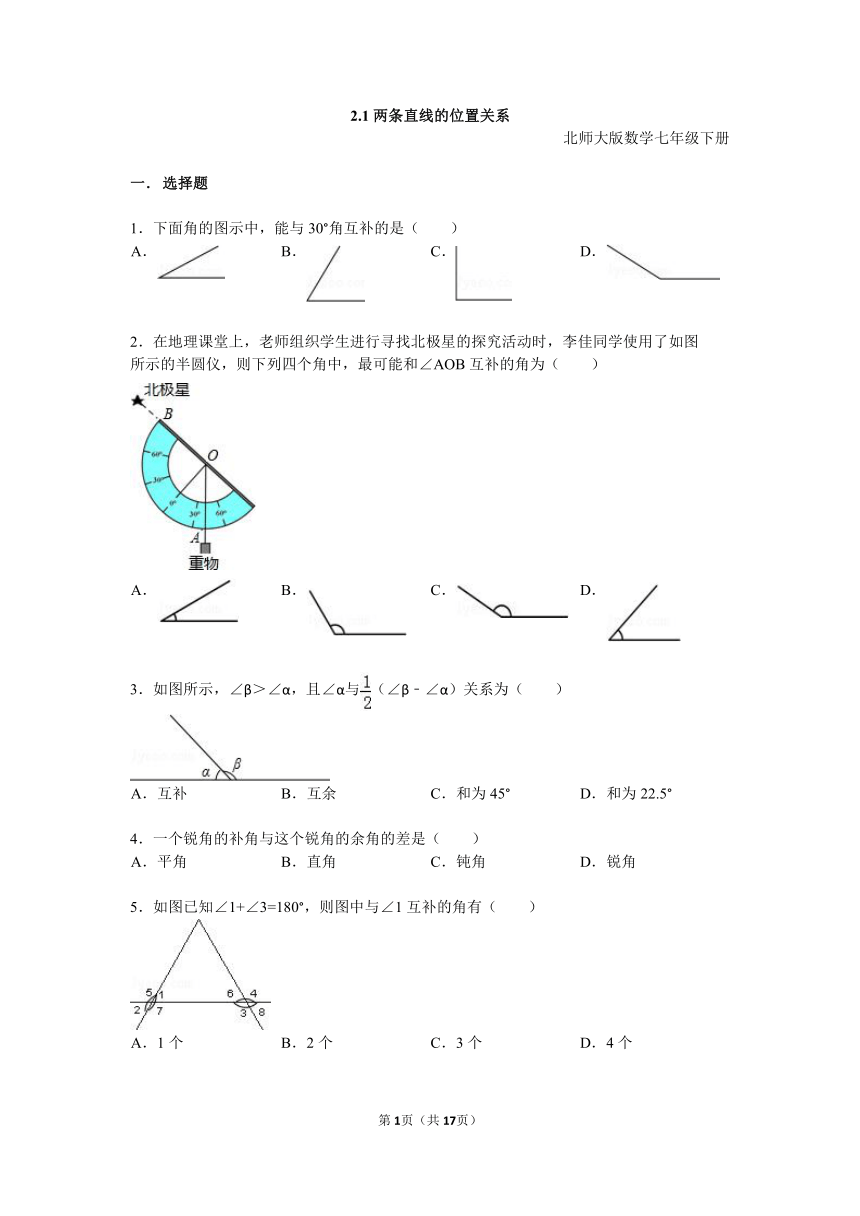 | |
| 格式 | zip | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-23 23:33:56 | ||
图片预览




文档简介
2.1两条直线的位置关系
北师大版数学七年级下册
选择题
1.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
2.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图
所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
A. B. C. D.
3.如图所示,∠β>∠α,且∠α与(∠β﹣∠α)关系为( )
A. 互补 B. 互余 C. 和为45° D. 和为22.5°
4.一个锐角的补角与这个锐角的余角的差是( )
A. 平角 B. 直角 C. 钝角 D. 锐角
5.如图已知∠1+∠3=180°,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.如图所示,点O在直线L上,∠1与∠2互余,∠α=116°,则∠β的度数是( )
A. 144° B. 164° C. 154° D. 150°
7.若一个角的补角的余角是28°,则这个角的度数为( )
A. 128° B. 118° C. 72° D. 62°
8.直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA、OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是( )
A. ∠BOD B. ∠AOC C. ∠COM D. 没有
9.以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A. ②③ B. ③ C. ①② D. ①
10.如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③180°﹣∠α;④(∠α﹣∠β).正确的是:( )
A. ①②③④ B. ①②④ C. ①②③ D. ①②
二.填空题
11.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度.
12.如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
余的角是 (只需填写三个角).
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
14.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= .
15.一副三角板按如图所示方式重叠,若图中∠DCE=35°25′,则∠ACB= .
三.解答题(共4小题)
16.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 对对顶角;
(5)若有2008条直线相交于一点,则可形成 对对顶角.
17.
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
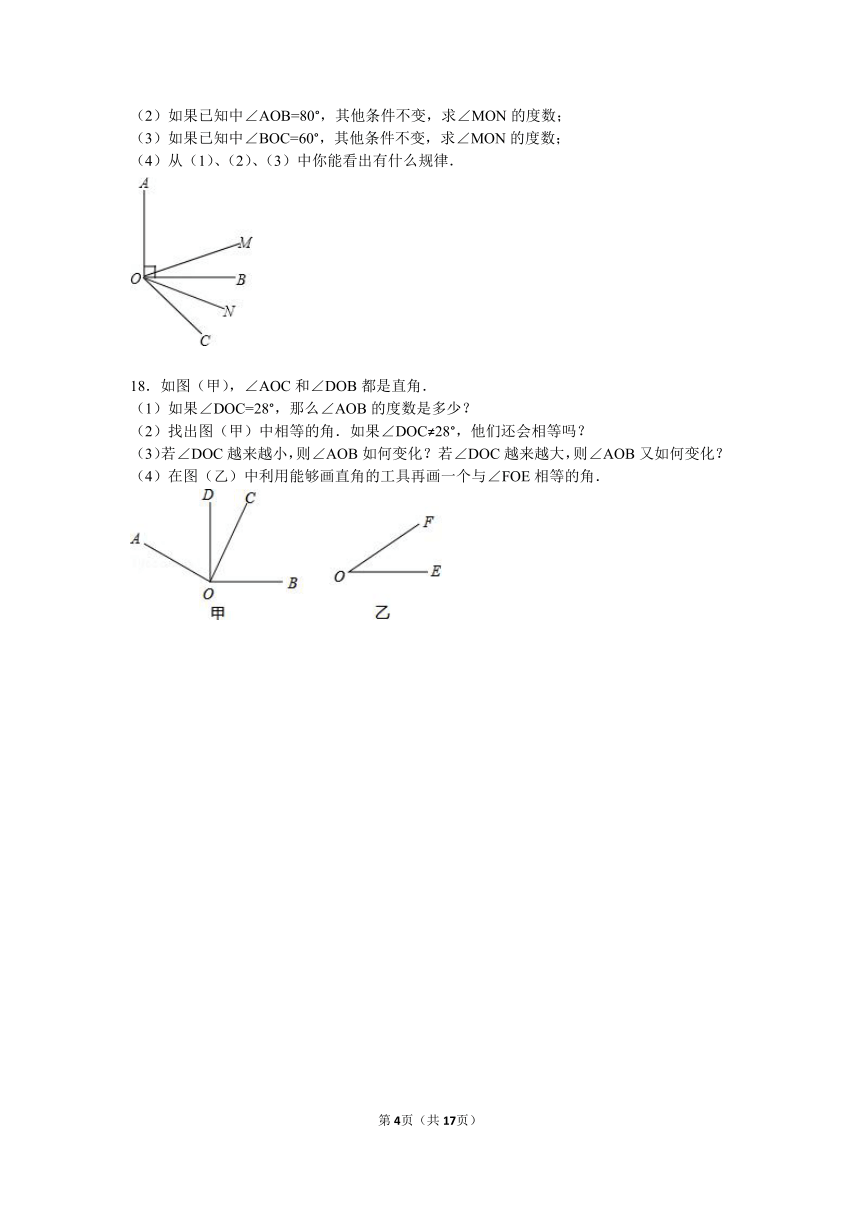
18.如图(甲),∠AOC和∠DOB都是直角.
(1)如果∠DOC=28°,那么∠AOB的度数是多少?
(2)找出图(甲)中相等的角.如果∠DOC≠28°,他们还会相等吗?
(3)若∠DOC越来越小,则∠AOB如何变化?若∠DOC越来越大,则∠AOB又如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与∠FOE相等的角.
参考答案与试题解析
一.选择题
1.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
答案:D
知识点: 余角和补角.
分析: 先求出30°的补角为150°,再测量度数等于150°的角即可求解.
解答: 解:30°角的补角=180°﹣30°=150°,是钝角,结合各图形,只有选项D是钝角,所以,能与30°角互补的是选项D.故选:D.
题型: 选择题
难易程度: 容易
掌握程度: 掌握
考查类型: 中考题型
试题类型: 精品型
试题级别: 七年级
试题地区: 广西省
试题来源: 2015年广西省玉林市中考数学试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了互为补角的定义,根据补角的定义求出30°角的补角是钝角是解题的关键.
2.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图
所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
A. B. C. D.
知识点: 余角和补角.
分析: 根据图形估计∠AOB的大致度数,然后根据互为补角的和等于180°进行解答即可.
解答: 解:根据图形可得∠AOB大约为135°,∴与∠AOB互补的角大约为45°,综合各选项D符合.故选D.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题型
试题级别: 七年级
试题来源: 2015年宝应县校级模拟
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角与补角的定义,熟记补角的概念,并大致估计出∠AOB的度数是解题的关键.
3.如图所示,∠β>∠α,且∠α与(∠β﹣∠α)关系为( )
A. 互补 B. 互余 C. 和为45° D. 和为22.5°
知识点: 余角和补角.
分析: 首先根据图形可得∠α+∠β=180°,再表示出∠α,然后再把等式变形即可.
解答: 解:观察图形可知,∠α+∠β=180°,则∠α=180°﹣∠β,∵180°﹣∠β+(∠β﹣∠α)=180°﹣(∠β+∠α)=180°﹣90°=90°.故∠α与(∠β﹣∠α)关系为互余.故选:B.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 常考型
试题类型: 普通类型
试题级别: 七年级
试题来源: 2015年杭州市中学模拟
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题主要考查了余角和补角,关键是掌握余角和补角的定义.
4.一个锐角的补角与这个锐角的余角的差是( )
A. 平角 B. 直角 C. 钝角 D. 锐角
知识点: 余角和补角.
分析: 首先根据余角与补角的定义,设这个角为x°,则它的余角为(90°﹣x),补角为(180°﹣x),再根据题中给出的关系列出代数式即可求解.
解答: 解:设这个角的度数为x,则它的余角为(90°﹣x),补角为(180°﹣x),则(180°﹣x)﹣(90°﹣x)=90°.故选B.
题型: 选择题
难易程度: 较易
掌握程度: 了解
考查类型: 常考题型
试题类型: 普通类型
试题级别: 七年级
试题来源 2015年启东市月考数学试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式求解.
5.如图已知∠1+∠3=180°,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
知识点: 对顶角、邻补角;余角和补角.
分析: 相加等于180°的两角称作互为补角,即两角互补.∠1的补角有它的两个邻补角∠5和∠7;另外∠1+∠3=180°,则∠3和它的对顶角∠4,都是∠1的补角.
解答: 解:从左边两条相交线看,∠1的邻补角有∠5和∠7;又∠1+∠3=180°,从右边两条相交线看,∠1的邻补角有∠3和∠4,共4个.故选D.
题型: 选择题
难易程度: 较易
掌握程度: 了解
考查类型: 常考题
试题类型: 普通类型
考察级别: 七年级
试题来源: 2015年昌江县校级数学期中考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题主要考查互补的概念以及对顶角的性质,是需要熟记的内容.
6.一个角的余角是它的补角的,则这个角为( )
A. 60° B. 45° C. 30° D. 90°
知识点: 余角和补角.
专题: 计算题.
分析: 先设出这个角,根据题中的数量关系列方程解答.
解答: 解:设这个角是x,列方程得:90°﹣x=(180°﹣x).解得x=45°.故选B.
题型: 选择题,计算题
难易程度: 普通
掌握程度: 掌握
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年郸城县校级数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 列方程时一定明确“余角是它的补角的”,不能误为(90°﹣x)=180°﹣x.
7.若一个角的补角的余角是28°,则这个角的度数为( )
A. 128° B. 118° C. 72° D. 62°
知识点: 余角和补角.
分析: 根据互余的两角之和为90°,互补的两角之和为180°,即可得出这个角的度数.
解答: 解:设这个角为x,由题意得,90°﹣(180°﹣x)=28°,解得:x=118°.故选:B.
题型: 选择题
难易程度: 容易
掌握程度: 了解
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年惠山区校级期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为90°,互补的两角之和为180°.
8.直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA、OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是( )
A. ∠BOD B. ∠AOC C. ∠COM D. 没有
知识点: 余角和补角;垂线.
分析: 根据垂直的定义,得∠AOM=∠BOM=90°,再结合图形和同角的余角相等可得始终与∠MOD保持相等的角.
解答: 解:∵OM⊥AB,∴∠AOM=∠BOM=90°.∴∠AOC+∠MOC=90°.∵∠COD是直角,∴∠DOM+∠MOC=90°.∴∠DOM=∠AOC.故选B.
题型: 选择题
难易程度: 容易
掌握程度: 常考
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年肥西县数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题利用垂直的定义和同角的余角相等,要注意领会由垂直得直角这一要点.
9.以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A. ②③ B. ③ C. ①② D. ①
知识点: 余角和补角;直线、射线、线段;直线的性质:两点确定一条直线.
分析: 根据线段的概念,直线的性质和余角、补角的定义进行判断.
解答: 解:①在同一直线上的4点A、B、C、D只能表示6条不同的线段,故错误;②经过两点有一条直线,并且只有一条直线,正确;③同一个锐角的补角一定大于它的余角,正确.故选A.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 好题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年宿州数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题综合考查线段的概念,直线的性质以及余角和补角的运用,属于基础题型.
10.如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③180°﹣∠α;④(∠α﹣∠β).正确的是:( )
A. ①②③④ B. ①②④ C. ①②③ D. ①②
知识点: 余角和补角.
分析: 根据∠α与∠β互补,得出∠β=180°﹣∠α,∠α=180°﹣∠β,求出∠β的余角是90°﹣∠β,90°﹣∠β表示∠β的余角;∠α﹣90°=90°﹣∠β,即可判断②;180°﹣∠α=∠β,根据余角的定义即可判断③;求出(∠α﹣∠β)=90°﹣∠β,即可判断④.
解答: 解:∵∠α与∠β互补,∴∠β=180°﹣∠α,∠α=180°﹣∠β,∴90°﹣∠β表示∠β的余角,∴①正确;∠α﹣90°=180°﹣∠β﹣90°=90°﹣∠β,∴②正确;180°﹣∠α=∠β,∴③错误;(∠α﹣∠β)=(180°﹣∠β﹣∠β)=90°﹣∠β,∴④正确;故选B.
题型: 选择题
难易程度: 普通
掌握程度: 掌握
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年靖江市数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了对余角和补角的理解和运用,注意:∠α与∠β互补,得出∠β=180°﹣∠α,∠α=180°﹣∠β;∠β的余角是90°﹣∠β,题目较好,难度不大.
二.填空题
11.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 90 度.
知识点: 对顶角、邻补角;余角和补角.
分析: 根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.
解答: 解:如图,∵∠1=∠3,∠2=∠4,而∠3+∠4=90°,∴∠1+∠2=90°.故答案为:90.
题型: 压轴题,计算题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2011年江西中考数学
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了对顶角的性质:对顶角相等.
12.如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
余的角是 ∠B′EM,∠MEB,∠A′NE (只需填写三个角).
知识点: 余角和补角;翻折变换(折叠问题).
分析: 由折叠的性质得到∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,再由平角的定义得到NE与ME垂直,根据同角(等角)的余角相等,即可在图中找出与∠B′ME互余的角.
解答: 解:由折叠及长方形ABCD可得:∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,∵∠MEB+∠MEB′+∠AEN+∠A′EN=180°,∴∠MEB+∠AEN=∠MEB′+∠A′EN=90°,则图中与∠B′ME互余的角是∠B′EM,∠MEB,∠A′NE.故答案为:∠B′EM,∠MEB,∠A′NE.
题型: 计算题,压轴题
难易程度: 较难
掌握类型: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年赵县数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查了余角和补角,以及翻折变换,熟练掌握图形折叠的性质是解本题的关键.
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 28 个交点.
知识点: 相交线.
专题: 压轴题;规律型.
分析: 由已知一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点总街出:在同一平面内,n条直线两两相交,则有 个交点,代入即可求解.
解答: 解:由已知总结出在同一平面内,n条直线两两相交,则有 个交点,所以8条直线两两相交,交点的个数为 =28,故答案为28个.故答案为:28.
题型: 压轴题,规律题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 无
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查的知识点是相交线,关键是此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊项一般猜想的方法.
14.(2014秋 故城县期末)如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= 180° .
知识点: 余角和补角.
分析: 因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
解答: 解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故答案为:180°.
题型: 填空题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 无
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
15.一副三角板按如图所示方式重叠,若图中∠DCE=35°25′,则∠ACB= 144°35′ .
知识点: 余角和补角.
分析: 因为∠ACB=∠ACD+∠DCB,∠ACD=90°,而∠DCB和∠DCE互余,利用互余的关系求得∠DCB解决问题.
解答: 解:∵∠DCB和∠DCE互余,∴∠DCB=90°﹣35°25′=54°35′,∠ACD=90°,∴∠ACB=∠ACD+∠DCB=90°+54°35′=144°35′.故答案为:144°35′.
题型: 填空题
难易程度: 较难
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014—2015年萧山区校级数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查角的和与差,注意利用三角板中的直角和两角互余的关系计算得出答案.
三.解答题(共4小题)
16.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 2 对对顶角;
(2)如图b,图中共有 6 对对顶角;
(3)如图c,图中共有 12 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 (n﹣1)n 对对顶角;
(5)若有2008条直线相交于一点,则可形成 4030056 对对顶角.
知识点: 相交线和对顶角
专题: 规律型.
分析: 由图示可得,(1)两条直线相交于一点,形成2对对顶角;(2)三条直线相交于一点,形成6对对顶角,(3)4条直线相交于一点,形成12对对顶角;(4)依次可找出规律,若有n条直线相交于一点,则可形成n(n﹣1)对对顶角;(5)将n=2008代入n(n﹣1),可得2008条直线相交于一点可形成的对顶角的对数.
解答: 解:(1)如图a,图中共有1×2=2对对顶角;(2)如图b,图中共有2×3=6对对顶角;(3)如图c,图中共有3×4=12对对顶角;(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n﹣1)对对顶角;(5)若有2008条直线相交于一点,则可形成(2008﹣1)×2008=4 030 056对对顶角.
题型: 规律型,压轴题,解答题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题,常考型
试题类型: 精品类型
试题级别: 七年级
试题来源: 2014—2015年铅山县校级数学月考试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查多条直线相交于一点,所形成的对顶角的个数的计算规律.即若有n条直线相交于一点,则可形成(n﹣1)n对对顶角.
17.如图,已知∠AOM与∠MOB互为余角,且∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
知识点: 余角和补角;角平分线的定义.
专题: 探究型.
分析: 要根据所提供的条件,和角平分线的性质,和两角互余的性质,求出角的度数.
解答: 解:(1)因OM平分∠AOC,所以∠MOC=∠AOC.又ON平分∠BOC,所以∠NOC=∠BOC.所以∠MON=∠MOC﹣∠NOC=∠AOC﹣∠BOC=∠AOB.而∠AOB=90°,所以∠MON=45度.(2)当∠AOB=80°,其他条件不变时,∠MON=×80°=40度.(3)当∠BOC=60°,其他条件不变时,∠MON=45度.(4)分析(1)、(2)、(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,而与锐角∠BOC的大小变化无关.
题型: 探究型,计算题,压轴题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题
试题类型: 精品类型
试题级别: 七年级
试题来源: 2013年莒南县数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 解题时要利用角平分线的性质和∠AOM与∠MOB互为余角找出各角之间的关系,求出各角的度数.
18.如图(甲),∠AOC和∠DOB都是直角.
(1)如果∠DOC=28°,那么∠AOB的度数是多少?
(2)找出图(甲)中相等的角.如果∠DOC≠28°,他们还会相等吗?
(3)若∠DOC越来越小,则∠AOB如何变化?若∠DOC越来越大,则∠AOB又如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与∠FOE相等的角.
知识点: 余角和补角;角的计算.
分析: (1)根据∠AOC=90°,∠DOC=28°,求出∠AOD的度数,然后即可求出∠AOB的度数;(2)根据等式的性质可得∠AOD=∠BOC;(3)根据∠AOD+∠DOC+∠DOC+∠BOC=180°,可得∠AOB+∠DOC=180°,进而得到∠DOC变小∠AOB变大,若∠DOC越来越大,则∠AOB越来越小.(4)首先以OE为边,在∠EOF外画∠GOE=90°,再以OF为边在∠EOF外画∠HOF=90°,即可得到∠HOG=∠EOF.
解答: 解:(1)因为,∠AOC=∠DOB=90°,∠DOC=28°所以,∠COB=90°﹣28°=62°所以,∠AOB=90°+62°=152°(2)相等的角有:∠AOC=∠DOB,∠AOD=∠COB如果∠DOC≠28°,他们还会相等(3)若∠DOC越来越小,则∠AOB越来越大;若∠DOC越来越大,则∠AOB越来越小(4)如图,画∠GOE=∠HOF=90°,则∠HOG=∠FOE即,∠HOG为所画的角
题型: 计算题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题
试题类型: 普通类型
试题级别: 七年级
试题来源 2013年秋年双柏县数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角和补角,以及角的计算,是基础题,准确识图是解题的关键.
第8页(共17页)
北师大版数学七年级下册
选择题
1.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
2.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图
所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
A. B. C. D.
3.如图所示,∠β>∠α,且∠α与(∠β﹣∠α)关系为( )
A. 互补 B. 互余 C. 和为45° D. 和为22.5°
4.一个锐角的补角与这个锐角的余角的差是( )
A. 平角 B. 直角 C. 钝角 D. 锐角
5.如图已知∠1+∠3=180°,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
6.如图所示,点O在直线L上,∠1与∠2互余,∠α=116°,则∠β的度数是( )
A. 144° B. 164° C. 154° D. 150°
7.若一个角的补角的余角是28°,则这个角的度数为( )
A. 128° B. 118° C. 72° D. 62°
8.直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA、OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是( )
A. ∠BOD B. ∠AOC C. ∠COM D. 没有
9.以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A. ②③ B. ③ C. ①② D. ①
10.如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③180°﹣∠α;④(∠α﹣∠β).正确的是:( )
A. ①②③④ B. ①②④ C. ①②③ D. ①②
二.填空题
11.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 度.
12.如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
余的角是 (只需填写三个角).
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 个交点.
14.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= .
15.一副三角板按如图所示方式重叠,若图中∠DCE=35°25′,则∠ACB= .
三.解答题(共4小题)
16.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3)如图c,图中共有 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 对对顶角;
(5)若有2008条直线相交于一点,则可形成 对对顶角.
17.
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
18.如图(甲),∠AOC和∠DOB都是直角.
(1)如果∠DOC=28°,那么∠AOB的度数是多少?
(2)找出图(甲)中相等的角.如果∠DOC≠28°,他们还会相等吗?
(3)若∠DOC越来越小,则∠AOB如何变化?若∠DOC越来越大,则∠AOB又如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与∠FOE相等的角.
参考答案与试题解析
一.选择题
1.下面角的图示中,能与30°角互补的是( )
A. B. C. D.
答案:D
知识点: 余角和补角.
分析: 先求出30°的补角为150°,再测量度数等于150°的角即可求解.
解答: 解:30°角的补角=180°﹣30°=150°,是钝角,结合各图形,只有选项D是钝角,所以,能与30°角互补的是选项D.故选:D.
题型: 选择题
难易程度: 容易
掌握程度: 掌握
考查类型: 中考题型
试题类型: 精品型
试题级别: 七年级
试题地区: 广西省
试题来源: 2015年广西省玉林市中考数学试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了互为补角的定义,根据补角的定义求出30°角的补角是钝角是解题的关键.
2.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图
所示的半圆仪,则下列四个角中,最可能和∠AOB互补的角为( )
A. B. C. D.
知识点: 余角和补角.
分析: 根据图形估计∠AOB的大致度数,然后根据互为补角的和等于180°进行解答即可.
解答: 解:根据图形可得∠AOB大约为135°,∴与∠AOB互补的角大约为45°,综合各选项D符合.故选D.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题型
试题级别: 七年级
试题来源: 2015年宝应县校级模拟
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角与补角的定义,熟记补角的概念,并大致估计出∠AOB的度数是解题的关键.
3.如图所示,∠β>∠α,且∠α与(∠β﹣∠α)关系为( )
A. 互补 B. 互余 C. 和为45° D. 和为22.5°
知识点: 余角和补角.
分析: 首先根据图形可得∠α+∠β=180°,再表示出∠α,然后再把等式变形即可.
解答: 解:观察图形可知,∠α+∠β=180°,则∠α=180°﹣∠β,∵180°﹣∠β+(∠β﹣∠α)=180°﹣(∠β+∠α)=180°﹣90°=90°.故∠α与(∠β﹣∠α)关系为互余.故选:B.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 常考型
试题类型: 普通类型
试题级别: 七年级
试题来源: 2015年杭州市中学模拟
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题主要考查了余角和补角,关键是掌握余角和补角的定义.
4.一个锐角的补角与这个锐角的余角的差是( )
A. 平角 B. 直角 C. 钝角 D. 锐角
知识点: 余角和补角.
分析: 首先根据余角与补角的定义,设这个角为x°,则它的余角为(90°﹣x),补角为(180°﹣x),再根据题中给出的关系列出代数式即可求解.
解答: 解:设这个角的度数为x,则它的余角为(90°﹣x),补角为(180°﹣x),则(180°﹣x)﹣(90°﹣x)=90°.故选B.
题型: 选择题
难易程度: 较易
掌握程度: 了解
考查类型: 常考题型
试题类型: 普通类型
试题级别: 七年级
试题来源 2015年启东市月考数学试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式求解.
5.如图已知∠1+∠3=180°,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
知识点: 对顶角、邻补角;余角和补角.
分析: 相加等于180°的两角称作互为补角,即两角互补.∠1的补角有它的两个邻补角∠5和∠7;另外∠1+∠3=180°,则∠3和它的对顶角∠4,都是∠1的补角.
解答: 解:从左边两条相交线看,∠1的邻补角有∠5和∠7;又∠1+∠3=180°,从右边两条相交线看,∠1的邻补角有∠3和∠4,共4个.故选D.
题型: 选择题
难易程度: 较易
掌握程度: 了解
考查类型: 常考题
试题类型: 普通类型
考察级别: 七年级
试题来源: 2015年昌江县校级数学期中考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题主要考查互补的概念以及对顶角的性质,是需要熟记的内容.
6.一个角的余角是它的补角的,则这个角为( )
A. 60° B. 45° C. 30° D. 90°
知识点: 余角和补角.
专题: 计算题.
分析: 先设出这个角,根据题中的数量关系列方程解答.
解答: 解:设这个角是x,列方程得:90°﹣x=(180°﹣x).解得x=45°.故选B.
题型: 选择题,计算题
难易程度: 普通
掌握程度: 掌握
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年郸城县校级数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 列方程时一定明确“余角是它的补角的”,不能误为(90°﹣x)=180°﹣x.
7.若一个角的补角的余角是28°,则这个角的度数为( )
A. 128° B. 118° C. 72° D. 62°
知识点: 余角和补角.
分析: 根据互余的两角之和为90°,互补的两角之和为180°,即可得出这个角的度数.
解答: 解:设这个角为x,由题意得,90°﹣(180°﹣x)=28°,解得:x=118°.故选:B.
题型: 选择题
难易程度: 容易
掌握程度: 了解
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年惠山区校级期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为90°,互补的两角之和为180°.
8.直线AB上有一点O,OM⊥AB于O,另有直角∠COD在平角∠AOB内绕O点左右摆动(OC与OA、OD与OB不重合),在摆动时,始终与∠MOD保持相等的角是( )
A. ∠BOD B. ∠AOC C. ∠COM D. 没有
知识点: 余角和补角;垂线.
分析: 根据垂直的定义,得∠AOM=∠BOM=90°,再结合图形和同角的余角相等可得始终与∠MOD保持相等的角.
解答: 解:∵OM⊥AB,∴∠AOM=∠BOM=90°.∴∠AOC+∠MOC=90°.∵∠COD是直角,∴∠DOM+∠MOC=90°.∴∠DOM=∠AOC.故选B.
题型: 选择题
难易程度: 容易
掌握程度: 常考
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年肥西县数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题利用垂直的定义和同角的余角相等,要注意领会由垂直得直角这一要点.
9.以下3个说法中:①在同一直线上的4点A、B、C、D只能表示5条不同的线段;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.说法都正确的结论是( )
A. ②③ B. ③ C. ①② D. ①
知识点: 余角和补角;直线、射线、线段;直线的性质:两点确定一条直线.
分析: 根据线段的概念,直线的性质和余角、补角的定义进行判断.
解答: 解:①在同一直线上的4点A、B、C、D只能表示6条不同的线段,故错误;②经过两点有一条直线,并且只有一条直线,正确;③同一个锐角的补角一定大于它的余角,正确.故选A.
题型: 选择题
难易程度: 普通
掌握程度: 理解
考查类型: 好题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014年宿州数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题综合考查线段的概念,直线的性质以及余角和补角的运用,属于基础题型.
10.如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③180°﹣∠α;④(∠α﹣∠β).正确的是:( )
A. ①②③④ B. ①②④ C. ①②③ D. ①②
知识点: 余角和补角.
分析: 根据∠α与∠β互补,得出∠β=180°﹣∠α,∠α=180°﹣∠β,求出∠β的余角是90°﹣∠β,90°﹣∠β表示∠β的余角;∠α﹣90°=90°﹣∠β,即可判断②;180°﹣∠α=∠β,根据余角的定义即可判断③;求出(∠α﹣∠β)=90°﹣∠β,即可判断④.
解答: 解:∵∠α与∠β互补,∴∠β=180°﹣∠α,∠α=180°﹣∠β,∴90°﹣∠β表示∠β的余角,∴①正确;∠α﹣90°=180°﹣∠β﹣90°=90°﹣∠β,∴②正确;180°﹣∠α=∠β,∴③错误;(∠α﹣∠β)=(180°﹣∠β﹣∠β)=90°﹣∠β,∴④正确;故选B.
题型: 选择题
难易程度: 普通
掌握程度: 掌握
考查类型: 易错题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年靖江市数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了对余角和补角的理解和运用,注意:∠α与∠β互补,得出∠β=180°﹣∠α,∠α=180°﹣∠β;∠β的余角是90°﹣∠β,题目较好,难度不大.
二.填空题
11.一块直角三角板放在两平行直线上,如图所示,∠1+∠2= 90 度.
知识点: 对顶角、邻补角;余角和补角.
分析: 根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.
解答: 解:如图,∵∠1=∠3,∠2=∠4,而∠3+∠4=90°,∴∠1+∠2=90°.故答案为:90.
题型: 压轴题,计算题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2011年江西中考数学
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了对顶角的性质:对顶角相等.
12.如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
余的角是 ∠B′EM,∠MEB,∠A′NE (只需填写三个角).
知识点: 余角和补角;翻折变换(折叠问题).
分析: 由折叠的性质得到∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,再由平角的定义得到NE与ME垂直,根据同角(等角)的余角相等,即可在图中找出与∠B′ME互余的角.
解答: 解:由折叠及长方形ABCD可得:∠MB′E=∠B=90°,∠NA′E=∠A=90°,∠MEB=∠MEB′,∠AEN=∠A′EN,∵∠MEB+∠MEB′+∠AEN+∠A′EN=180°,∴∠MEB+∠AEN=∠MEB′+∠A′EN=90°,则图中与∠B′ME互余的角是∠B′EM,∠MEB,∠A′NE.故答案为:∠B′EM,∠MEB,∠A′NE.
题型: 计算题,压轴题
难易程度: 较难
掌握类型: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2013年赵县数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查了余角和补角,以及翻折变换,熟练掌握图形折叠的性质是解本题的关键.
13.一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点;8条直线两两相交,最多有 28 个交点.
知识点: 相交线.
专题: 压轴题;规律型.
分析: 由已知一平面内,三条直线两两相交,最多有3个交点;4条直线两两相交,最多有6个交点;5条直线两两相交,最多有10个交点总街出:在同一平面内,n条直线两两相交,则有 个交点,代入即可求解.
解答: 解:由已知总结出在同一平面内,n条直线两两相交,则有 个交点,所以8条直线两两相交,交点的个数为 =28,故答案为28个.故答案为:28.
题型: 压轴题,规律题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 无
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查的知识点是相交线,关键是此题在相交线的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊项一般猜想的方法.
14.(2014秋 故城县期末)如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= 180° .
知识点: 余角和补角.
分析: 因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
解答: 解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故答案为:180°.
题型: 填空题
难易程度: 普通
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 无
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
15.一副三角板按如图所示方式重叠,若图中∠DCE=35°25′,则∠ACB= 144°35′ .
知识点: 余角和补角.
分析: 因为∠ACB=∠ACD+∠DCB,∠ACD=90°,而∠DCB和∠DCE互余,利用互余的关系求得∠DCB解决问题.
解答: 解:∵∠DCB和∠DCE互余,∴∠DCB=90°﹣35°25′=54°35′,∠ACD=90°,∴∠ACB=∠ACD+∠DCB=90°+54°35′=144°35′.故答案为:144°35′.
题型: 填空题
难易程度: 较难
掌握程度: 理解
考查类型: 常考题
试题类型: 普通类型
试题级别: 七年级
试题来源: 2014—2015年萧山区校级数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 此题考查角的和与差,注意利用三角板中的直角和两角互余的关系计算得出答案.
三.解答题(共4小题)
16.观察下列各图,寻找对顶角(不含平角):
(1)如图a,图中共有 2 对对顶角;
(2)如图b,图中共有 6 对对顶角;
(3)如图c,图中共有 12 对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成 (n﹣1)n 对对顶角;
(5)若有2008条直线相交于一点,则可形成 4030056 对对顶角.
知识点: 相交线和对顶角
专题: 规律型.
分析: 由图示可得,(1)两条直线相交于一点,形成2对对顶角;(2)三条直线相交于一点,形成6对对顶角,(3)4条直线相交于一点,形成12对对顶角;(4)依次可找出规律,若有n条直线相交于一点,则可形成n(n﹣1)对对顶角;(5)将n=2008代入n(n﹣1),可得2008条直线相交于一点可形成的对顶角的对数.
解答: 解:(1)如图a,图中共有1×2=2对对顶角;(2)如图b,图中共有2×3=6对对顶角;(3)如图c,图中共有3×4=12对对顶角;(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n﹣1)对对顶角;(5)若有2008条直线相交于一点,则可形成(2008﹣1)×2008=4 030 056对对顶角.
题型: 规律型,压轴题,解答题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题,常考型
试题类型: 精品类型
试题级别: 七年级
试题来源: 2014—2015年铅山县校级数学月考试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查多条直线相交于一点,所形成的对顶角的个数的计算规律.即若有n条直线相交于一点,则可形成(n﹣1)n对对顶角.
17.如图,已知∠AOM与∠MOB互为余角,且∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)如果已知中∠AOB=80°,其他条件不变,求∠MON的度数;
(3)如果已知中∠BOC=60°,其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)中你能看出有什么规律.
知识点: 余角和补角;角平分线的定义.
专题: 探究型.
分析: 要根据所提供的条件,和角平分线的性质,和两角互余的性质,求出角的度数.
解答: 解:(1)因OM平分∠AOC,所以∠MOC=∠AOC.又ON平分∠BOC,所以∠NOC=∠BOC.所以∠MON=∠MOC﹣∠NOC=∠AOC﹣∠BOC=∠AOB.而∠AOB=90°,所以∠MON=45度.(2)当∠AOB=80°,其他条件不变时,∠MON=×80°=40度.(3)当∠BOC=60°,其他条件不变时,∠MON=45度.(4)分析(1)、(2)、(3)的结果和(1)的解答过程可知:∠MON的大小总等于∠AOB的一半,而与锐角∠BOC的大小变化无关.
题型: 探究型,计算题,压轴题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题
试题类型: 精品类型
试题级别: 七年级
试题来源: 2013年莒南县数学期末考试
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 解题时要利用角平分线的性质和∠AOM与∠MOB互为余角找出各角之间的关系,求出各角的度数.
18.如图(甲),∠AOC和∠DOB都是直角.
(1)如果∠DOC=28°,那么∠AOB的度数是多少?
(2)找出图(甲)中相等的角.如果∠DOC≠28°,他们还会相等吗?
(3)若∠DOC越来越小,则∠AOB如何变化?若∠DOC越来越大,则∠AOB又如何变化?
(4)在图(乙)中利用能够画直角的工具再画一个与∠FOE相等的角.
知识点: 余角和补角;角的计算.
分析: (1)根据∠AOC=90°,∠DOC=28°,求出∠AOD的度数,然后即可求出∠AOB的度数;(2)根据等式的性质可得∠AOD=∠BOC;(3)根据∠AOD+∠DOC+∠DOC+∠BOC=180°,可得∠AOB+∠DOC=180°,进而得到∠DOC变小∠AOB变大,若∠DOC越来越大,则∠AOB越来越小.(4)首先以OE为边,在∠EOF外画∠GOE=90°,再以OF为边在∠EOF外画∠HOF=90°,即可得到∠HOG=∠EOF.
解答: 解:(1)因为,∠AOC=∠DOB=90°,∠DOC=28°所以,∠COB=90°﹣28°=62°所以,∠AOB=90°+62°=152°(2)相等的角有:∠AOC=∠DOB,∠AOD=∠COB如果∠DOC≠28°,他们还会相等(3)若∠DOC越来越小,则∠AOB越来越大;若∠DOC越来越大,则∠AOB越来越小(4)如图,画∠GOE=∠HOF=90°,则∠HOG=∠FOE即,∠HOG为所画的角
题型: 计算题
难易程度: 较难
掌握程度: 理解
考查类型: 压轴题
试题类型: 普通类型
试题级别: 七年级
试题来源 2013年秋年双柏县数学期末考试试卷
试题标签: 北师大版 数学 七年级下学期 第二章第一节
点评: 本题考查了余角和补角,以及角的计算,是基础题,准确识图是解题的关键.
第8页(共17页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
