第八章 8.3.1 棱柱、棱锥、棱台的表面积和体积 课时练(含答案)
文档属性
| 名称 | 第八章 8.3.1 棱柱、棱锥、棱台的表面积和体积 课时练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 00:00:00 | ||
图片预览




文档简介
§8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.若正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
2.已知一直棱柱底面为正方形,它的底面边长为2,体对角线长为4,则这个棱柱的表面积是( )
A.8 B.16
C.8+12 D.8+16
3.在我国瓷器的历史上,六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以许多瓷器都做成六棱形和八棱形的,但是六棱柱形的瓷器只有六棱柱形笔筒,其余的六棱形都不是六棱柱形.如图为一个正六棱柱形状的瓷器笔筒,高为18.7 cm,底面边长为7 cm(数据为笔筒的外观数据),用一层绒布将其侧面包裹住,忽略绒布的厚度,则至少需要绒布的面积为( )
A.120 cm2 B.162.7 cm2
C.785.4 cm2 D.1 570.8 cm2
4.如图,ABC-A′B′C′是体积为1的三棱柱,则四棱锥C-AA′B′B的体积是( )
A. B.
C. D.
5.(多选)已知正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥的高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥的侧面积为
6.如图1所示,已知正方体的面对角线长为a,沿阴影面将它切割成两块,拼成如图2所示的几何体,那么此几何体的表面积为( )
A.(1+2)a2 B.(2+)a2
C.a2 D.a2
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
8.如图,一个棱长为4的正方体被挖去一个高为4的正四棱柱后得到图中的几何体,若该几何体的体积为60,则该几何体的表面积为________.
9.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积、表面积.
10.如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
(1)求大棱锥、小棱锥、棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12 cm,小棱锥的底面边长为4 cm,求截得的棱台的侧面面积和表面积.
11.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分几何体,且上、下两部分的高之比为1∶2,则关于上、下两几何体的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
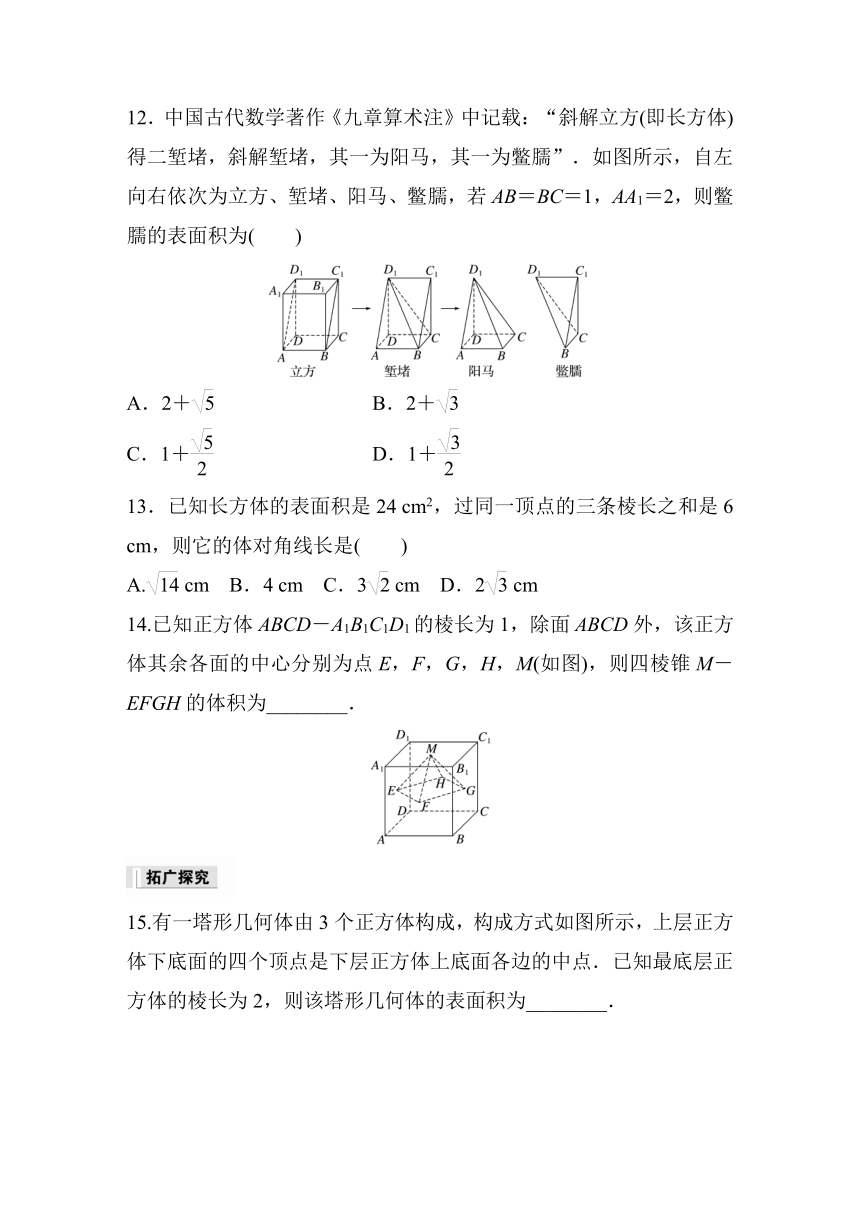
12.中国古代数学著作《九章算术注》中记载:“斜解立方(即长方体)得二堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.如图所示,自左向右依次为立方、堑堵、阳马、鳖臑,若AB=BC=1,AA1=2,则鳖臑的表面积为( )
A.2+ B.2+
C.1+ D.1+
13.已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是( )
A. cm B.4 cm C.3 cm D.2 cm
14.已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
15.有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形几何体的表面积为________.
16.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.B 2.D 3.C 4.C
5.ABD [如图所示,设E为等边三角形ADC的中心,F为CD的中点,连接PF,EF,PE,则PE为正三棱锥的高,PF为斜高,又PF==,EF=×3×=,故PE==3,故A,B正确;正三棱锥的体积为×3××9=,侧面积为3××3×=,故C错误,D正确.
]
6.D [因为正方体的面对角线长为a,则其棱长为a,
图2所示的几何体是平行六面体,上下,左右,前后两两的面积分别相等,
上、下底面是长和宽分别为a和a的矩形,其面积均为a×a=a2,
前、后两个面是两个全等的等腰直角三角形拼成的平行四边形,其面积均为2××a×a=a2,
左、右两个面是边长为a的正方形,其面积均为a×a=a2,
则此几何体的表面积为
2=a2.]
7.1 8.110
9.解 如图,设底面对角线AC=a,BD=b,
交点为O,
体对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2=2+2
===64,
∴AB=8.∴直四棱柱的侧面积
S侧=4×8×5=160.
直四棱柱的底面积
S底=AC·BD=20.
直四棱柱的表面积
S表=160+2×20=160+40.
10.解 (1)由题意知S小棱锥侧∶S大棱锥侧=1∶4,则S大棱锥侧∶S小棱锥侧∶S棱台侧=4∶1∶3.
(2)如图所示,
∵小棱锥的底面边长为4 cm,
∴大棱锥的底面边长为8 cm,
又PA=12 cm,
∴A1A=6 cm.
又梯形ABB1A1的高h′==4(cm),
∴S棱台侧=6××4
=144(cm2),
∴S棱台表=S棱台侧+S上底+S下底=144+24+96=(144+120) cm2.
11.BD
12.A [由题意可知鳖臑为四个面均是直角三角形的四面体.
∵长方体ABCD-A1B1C1D1的长、宽、高分别为1,1,2,
∴C1D1=1,C1C=2,C1B=D1C==,
∴鳖臑的表面积S==+++=2+.]
13.D [设过同一顶点的三条棱长分别为a cm,b cm,c cm ,体对角线长为l cm,则a+b+c=6,且2(ab+bc+ca)=24,从而l==
==2(cm).]
14.
解析 连接AD1,CD1,B1A,B1C,AC(图略),
∵E,H分别为AD1,CD1的中点,
∴EH∥AC,EH=AC=.
同理可得FG∥AC,
FG=AC=,
∴EH∥FG,EH=FG,
∴四边形EFGH为平行四边形,
又EG=HF,EH=HG,
∴四边形EFGH为正方形.
又四棱锥M-EFGH的高为,
∴四棱锥M-EFGH的体积为×2×=.
15.36
解析 易知由下向上三个正方体的棱长依次为2,,1,
∴S表=2×22+4×[22+()2+12]=36.
∴该几何体的表面积为36.
16.解 设点B到平面EMC的距离为h1,点D到平面EMC的距离为h2,
连接MD,因为M是AE的中点,
所以VM-ABCD=V,
所以VE-MBC=V-VE-MDC.
而VE-MBC=VB-EMC,VE-MDC=VD-EMC,
所以==.
因为B,D到平面EMC的距离即为到平面EAC的距离,而AB∥CD,且2AB=3CD,所以=.
所以VE-MBC=VM-EBC=V.
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.若正方体的表面积为96,则正方体的体积为( )
A.48 B.64 C.16 D.96
2.已知一直棱柱底面为正方形,它的底面边长为2,体对角线长为4,则这个棱柱的表面积是( )
A.8 B.16
C.8+12 D.8+16
3.在我国瓷器的历史上,六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以许多瓷器都做成六棱形和八棱形的,但是六棱柱形的瓷器只有六棱柱形笔筒,其余的六棱形都不是六棱柱形.如图为一个正六棱柱形状的瓷器笔筒,高为18.7 cm,底面边长为7 cm(数据为笔筒的外观数据),用一层绒布将其侧面包裹住,忽略绒布的厚度,则至少需要绒布的面积为( )
A.120 cm2 B.162.7 cm2
C.785.4 cm2 D.1 570.8 cm2
4.如图,ABC-A′B′C′是体积为1的三棱柱,则四棱锥C-AA′B′B的体积是( )
A. B.
C. D.
5.(多选)已知正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥的高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥的侧面积为
6.如图1所示,已知正方体的面对角线长为a,沿阴影面将它切割成两块,拼成如图2所示的几何体,那么此几何体的表面积为( )
A.(1+2)a2 B.(2+)a2
C.a2 D.a2
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
8.如图,一个棱长为4的正方体被挖去一个高为4的正四棱柱后得到图中的几何体,若该几何体的体积为60,则该几何体的表面积为________.
9.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积、表面积.
10.如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
(1)求大棱锥、小棱锥、棱台的侧面面积之比;
(2)若大棱锥PO的侧棱长为12 cm,小棱锥的底面边长为4 cm,求截得的棱台的侧面面积和表面积.
11.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分几何体,且上、下两部分的高之比为1∶2,则关于上、下两几何体的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
12.中国古代数学著作《九章算术注》中记载:“斜解立方(即长方体)得二堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.如图所示,自左向右依次为立方、堑堵、阳马、鳖臑,若AB=BC=1,AA1=2,则鳖臑的表面积为( )
A.2+ B.2+
C.1+ D.1+
13.已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是( )
A. cm B.4 cm C.3 cm D.2 cm
14.已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
15.有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,则该塔形几何体的表面积为________.
16.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.B 2.D 3.C 4.C
5.ABD [如图所示,设E为等边三角形ADC的中心,F为CD的中点,连接PF,EF,PE,则PE为正三棱锥的高,PF为斜高,又PF==,EF=×3×=,故PE==3,故A,B正确;正三棱锥的体积为×3××9=,侧面积为3××3×=,故C错误,D正确.
]
6.D [因为正方体的面对角线长为a,则其棱长为a,
图2所示的几何体是平行六面体,上下,左右,前后两两的面积分别相等,
上、下底面是长和宽分别为a和a的矩形,其面积均为a×a=a2,
前、后两个面是两个全等的等腰直角三角形拼成的平行四边形,其面积均为2××a×a=a2,
左、右两个面是边长为a的正方形,其面积均为a×a=a2,
则此几何体的表面积为
2=a2.]
7.1 8.110
9.解 如图,设底面对角线AC=a,BD=b,
交点为O,
体对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2=2+2
===64,
∴AB=8.∴直四棱柱的侧面积
S侧=4×8×5=160.
直四棱柱的底面积
S底=AC·BD=20.
直四棱柱的表面积
S表=160+2×20=160+40.
10.解 (1)由题意知S小棱锥侧∶S大棱锥侧=1∶4,则S大棱锥侧∶S小棱锥侧∶S棱台侧=4∶1∶3.
(2)如图所示,
∵小棱锥的底面边长为4 cm,
∴大棱锥的底面边长为8 cm,
又PA=12 cm,
∴A1A=6 cm.
又梯形ABB1A1的高h′==4(cm),
∴S棱台侧=6××4
=144(cm2),
∴S棱台表=S棱台侧+S上底+S下底=144+24+96=(144+120) cm2.
11.BD
12.A [由题意可知鳖臑为四个面均是直角三角形的四面体.
∵长方体ABCD-A1B1C1D1的长、宽、高分别为1,1,2,
∴C1D1=1,C1C=2,C1B=D1C==,
∴鳖臑的表面积S==+++=2+.]
13.D [设过同一顶点的三条棱长分别为a cm,b cm,c cm ,体对角线长为l cm,则a+b+c=6,且2(ab+bc+ca)=24,从而l==
==2(cm).]
14.
解析 连接AD1,CD1,B1A,B1C,AC(图略),
∵E,H分别为AD1,CD1的中点,
∴EH∥AC,EH=AC=.
同理可得FG∥AC,
FG=AC=,
∴EH∥FG,EH=FG,
∴四边形EFGH为平行四边形,
又EG=HF,EH=HG,
∴四边形EFGH为正方形.
又四棱锥M-EFGH的高为,
∴四棱锥M-EFGH的体积为×2×=.
15.36
解析 易知由下向上三个正方体的棱长依次为2,,1,
∴S表=2×22+4×[22+()2+12]=36.
∴该几何体的表面积为36.
16.解 设点B到平面EMC的距离为h1,点D到平面EMC的距离为h2,
连接MD,因为M是AE的中点,
所以VM-ABCD=V,
所以VE-MBC=V-VE-MDC.
而VE-MBC=VB-EMC,VE-MDC=VD-EMC,
所以==.
因为B,D到平面EMC的距离即为到平面EAC的距离,而AB∥CD,且2AB=3CD,所以=.
所以VE-MBC=VM-EBC=V.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
