第八章 8.3.2 圆柱、圆锥、圆台、球的表面积和体积 课时练(含答案)
文档属性
| 名称 | 第八章 8.3.2 圆柱、圆锥、圆台、球的表面积和体积 课时练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 07:50:09 | ||
图片预览


文档简介
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1.两个球的体积之比为8∶27,那么这两个球的表面积之比为( )
A.2∶3 B.4∶9
C.∶ D.2∶3
2.轴截面是正三角形的圆锥称为等边圆锥,则等边圆锥的侧面积是底面积的( )
A.4倍 B.3倍 C.倍 D.2倍
3.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式d≈.如果球的半径为,根据“开立圆术”的方法求得的球的体积约为( )
A. B. C. D.
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B.
C.2π D.4π
5.(多选)圆台的上、下底面半径分别为10和20,它的侧面展开所得的扇环所对的圆心角为180°,则圆台的( )
A.母线长为20 B.表面积为1 100π
C.高为10 D.体积为
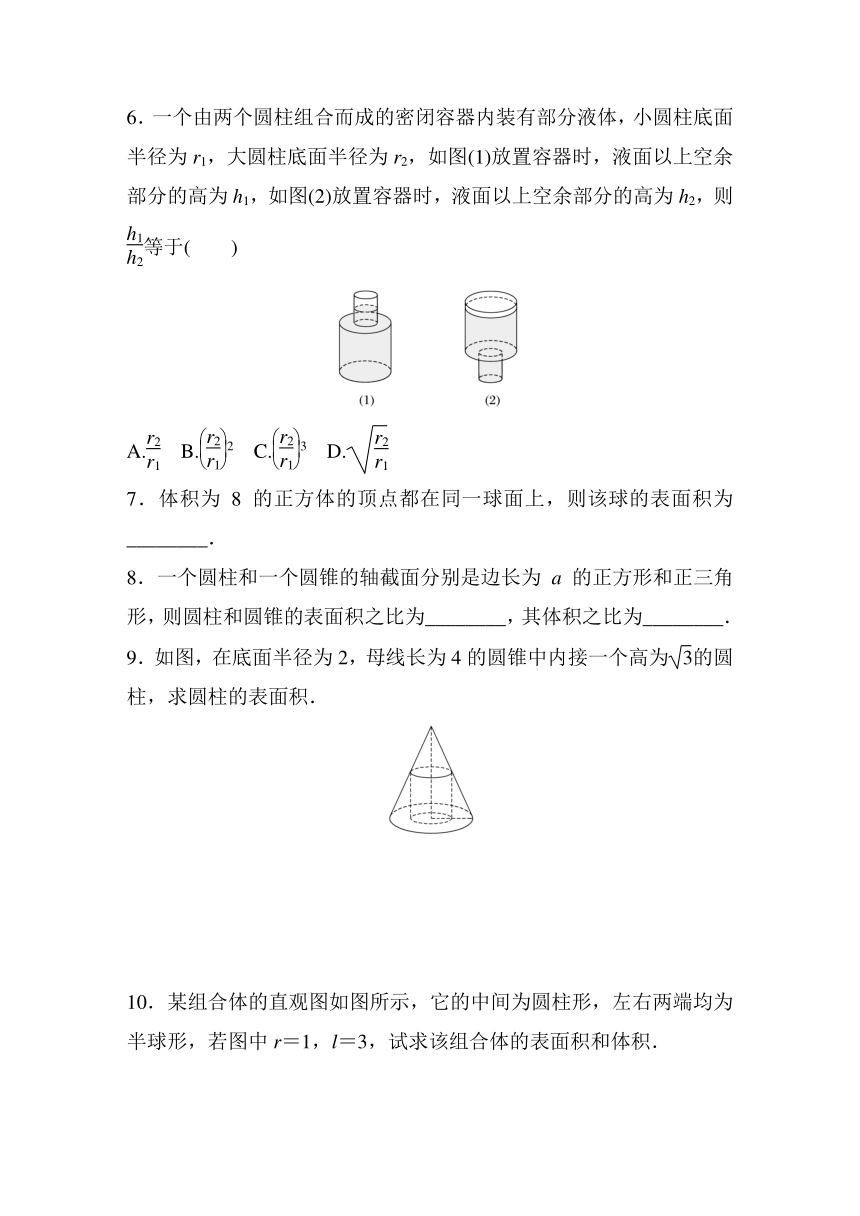
6.一个由两个圆柱组合而成的密闭容器内装有部分液体,小圆柱底面半径为r1,大圆柱底面半径为r2,如图(1)放置容器时,液面以上空余部分的高为h1,如图(2)放置容器时,液面以上空余部分的高为h2,则等于( )
A. B.2 C.3 D.
7.体积为8的正方体的顶点都在同一球面上,则该球的表面积为________.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
9.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为( )
A.5π B.6π C.20π D.10π
12.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸,若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)( )
A.2寸 B.3寸 C.4寸 D.6寸
13.祖暅,祖冲之之子,南北朝时期伟大的科学家,于5世纪末提出下面的体积计算原理,即祖暅原理:幂势既同,则积不容异.意思是如果两个等高的几何体在同高处截得两几何体的截面面积相等,那么这两个几何体的体积相等,现有如图的半椭球体与被挖去圆锥的圆柱等高,且平行于底面的平面在任意高度截两几何体所得截面面积相等,已知圆柱高为h,底面半径为r,则半椭球的体积是________.
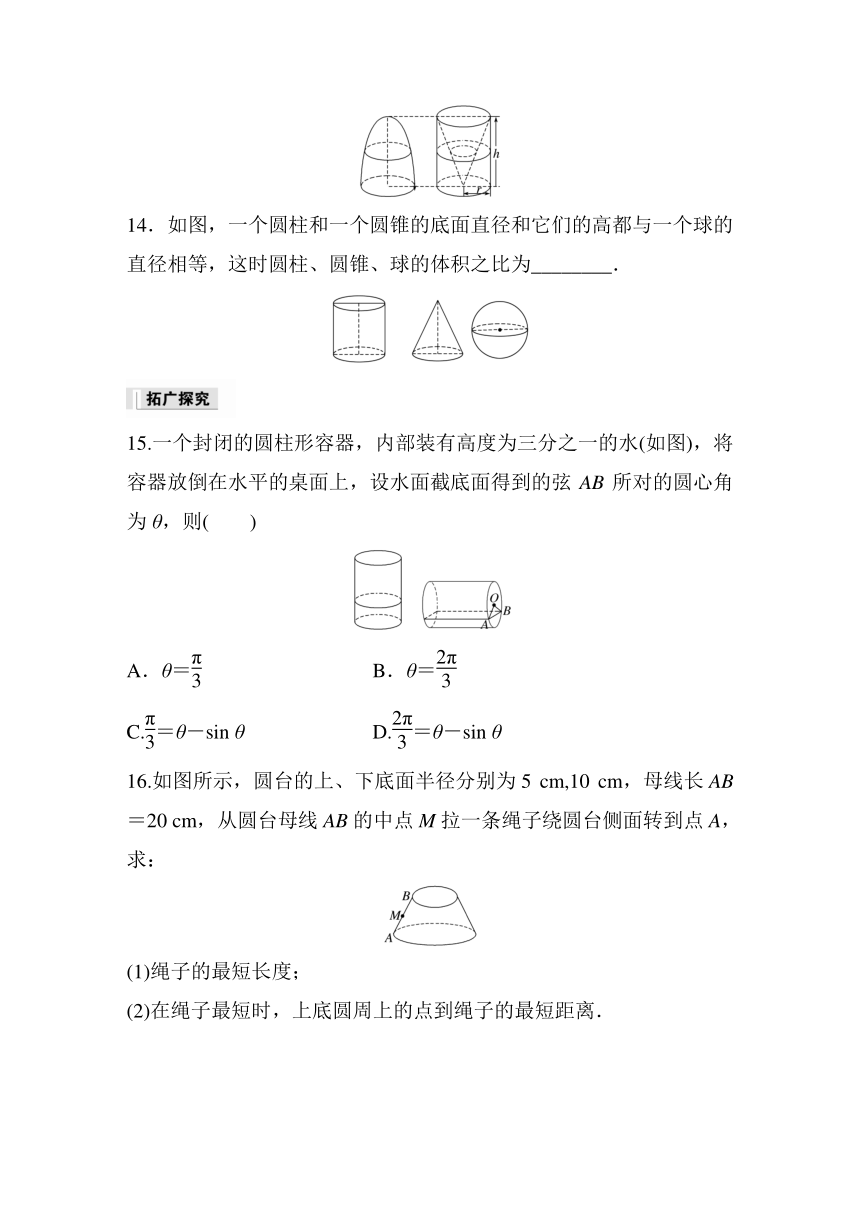
14.如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的体积之比为________.
15.一个封闭的圆柱形容器,内部装有高度为三分之一的水(如图),将容器放倒在水平的桌面上,设水面截底面得到的弦AB所对的圆心角为θ,则( )
A.θ= B.θ=
C.=θ-sin θ D.=θ-sin θ
16.如图所示,圆台的上、下底面半径分别为5 cm,10 cm,母线长AB=20 cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到点A,求:
(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1.B 2.D 3.D 4.B
5.ABD [如图所示,设圆台的上底面周长为C,因为扇环所对的圆心角为180°,
所以C=π·SA,
又C=10×2π,
所以SA=20,
同理SB=40,
故圆台的母线AB=SB-SA=20,
高h==10,
体积V=π×10×(102+10×20+202)=,
表面积S=π(10+20)×20+100π+400π=1 100π,
故A,B,D正确,C错误.]
6.B [在图(1)中,液面以上空余部分的体积为πrh1;在图(2)中,液面以上空余部分的体积为πrh2.因为πrh1=πrh2,所以=2.]
7.12π
8.2∶1 2∶1
解析 S圆柱=2·π2+2π··a=a2.
S圆锥=π2+π··a=a2.
∴S圆柱∶S圆锥=2∶1.
V圆柱=π2·a=a3,
V圆锥=·π2·a=a3,
∴V圆柱∶V圆锥=a3∶a3
=2∶1.
9.解 设圆锥的底面半径为R,圆柱的底面半径为r,高为h,表面积为S.
则R=OC=2,AC=4,AO==2,h=,AE=AO-h=.
如图所示,易知△AEB∽△AOC,
∴=,
即=,∴r=1,
∴S=S圆柱底+S圆柱侧=2π+2π=(2+2)π.
10.解 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π.
该组合体的体积V=πr3+πr2l
=π×13+π×12×3=.
11.D
12.B [由已知得,天池盆盆口半径为14寸,盆底半径为6寸,
则盆口面积为196π,盆底面积为36π,
又盆深18寸,盆中水深9寸,
则积水水面的半径为=10(寸),
∴积水水面面积为100π,
∴积水的体积V=×(36π++100π)×9=588π,
∴平地降雨量为=3(寸).]
13.πr2h
解析 依题意可得V=V圆柱-V圆锥
=πr2·h-·πr2·h=πr2h.
14.3∶1∶2
解析 设球的半径为R,则
V圆柱=πR2·2R=2πR3,
V圆锥=πR2·2R=πR3,
V球=πR3,
故V圆柱∶V圆锥∶V球
=2πR3∶πR3∶πR3
=3∶1∶2.
15.D [设圆柱底面半径为r,高为h,
则水的体积为πr2h.
水平放置后,水的体积为h,
所以πr2h=h,
整理得=θ-sin θ.]
16.解 (1)如图所示,将侧面展开,绳子的最短长度为侧面展开图中AM的长度,
设OB=l,∠AOA′=θ,
则θ·l=2π×5,
θ·(l+20)=2π×10,
解得θ=,l=20(cm).
∴OA=40(cm),OM=30(cm).
∴AM==50(cm).
即绳子的最短长度为50 cm.
(2)如图所示,作OQ⊥AM于点Q,交弧BB′于点P,
则PQ即为所求的最短距离.
∵OA·OM=AM·OQ,
∴OQ=24(cm).
故PQ=OQ-OP=24-20=4(cm),即上底圆周上的点到绳子的最短距离为4 cm.
1.两个球的体积之比为8∶27,那么这两个球的表面积之比为( )
A.2∶3 B.4∶9
C.∶ D.2∶3
2.轴截面是正三角形的圆锥称为等边圆锥,则等边圆锥的侧面积是底面积的( )
A.4倍 B.3倍 C.倍 D.2倍
3.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式d≈.如果球的半径为,根据“开立圆术”的方法求得的球的体积约为( )
A. B. C. D.
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B.
C.2π D.4π
5.(多选)圆台的上、下底面半径分别为10和20,它的侧面展开所得的扇环所对的圆心角为180°,则圆台的( )
A.母线长为20 B.表面积为1 100π
C.高为10 D.体积为
6.一个由两个圆柱组合而成的密闭容器内装有部分液体,小圆柱底面半径为r1,大圆柱底面半径为r2,如图(1)放置容器时,液面以上空余部分的高为h1,如图(2)放置容器时,液面以上空余部分的高为h2,则等于( )
A. B.2 C.3 D.
7.体积为8的正方体的顶点都在同一球面上,则该球的表面积为________.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
9.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为( )
A.5π B.6π C.20π D.10π
12.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸,若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)( )
A.2寸 B.3寸 C.4寸 D.6寸
13.祖暅,祖冲之之子,南北朝时期伟大的科学家,于5世纪末提出下面的体积计算原理,即祖暅原理:幂势既同,则积不容异.意思是如果两个等高的几何体在同高处截得两几何体的截面面积相等,那么这两个几何体的体积相等,现有如图的半椭球体与被挖去圆锥的圆柱等高,且平行于底面的平面在任意高度截两几何体所得截面面积相等,已知圆柱高为h,底面半径为r,则半椭球的体积是________.
14.如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的体积之比为________.
15.一个封闭的圆柱形容器,内部装有高度为三分之一的水(如图),将容器放倒在水平的桌面上,设水面截底面得到的弦AB所对的圆心角为θ,则( )
A.θ= B.θ=
C.=θ-sin θ D.=θ-sin θ
16.如图所示,圆台的上、下底面半径分别为5 cm,10 cm,母线长AB=20 cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到点A,求:
(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
1.B 2.D 3.D 4.B
5.ABD [如图所示,设圆台的上底面周长为C,因为扇环所对的圆心角为180°,
所以C=π·SA,
又C=10×2π,
所以SA=20,
同理SB=40,
故圆台的母线AB=SB-SA=20,
高h==10,
体积V=π×10×(102+10×20+202)=,
表面积S=π(10+20)×20+100π+400π=1 100π,
故A,B,D正确,C错误.]
6.B [在图(1)中,液面以上空余部分的体积为πrh1;在图(2)中,液面以上空余部分的体积为πrh2.因为πrh1=πrh2,所以=2.]
7.12π
8.2∶1 2∶1
解析 S圆柱=2·π2+2π··a=a2.
S圆锥=π2+π··a=a2.
∴S圆柱∶S圆锥=2∶1.
V圆柱=π2·a=a3,
V圆锥=·π2·a=a3,
∴V圆柱∶V圆锥=a3∶a3
=2∶1.
9.解 设圆锥的底面半径为R,圆柱的底面半径为r,高为h,表面积为S.
则R=OC=2,AC=4,AO==2,h=,AE=AO-h=.
如图所示,易知△AEB∽△AOC,
∴=,
即=,∴r=1,
∴S=S圆柱底+S圆柱侧=2π+2π=(2+2)π.
10.解 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π.
该组合体的体积V=πr3+πr2l
=π×13+π×12×3=.
11.D
12.B [由已知得,天池盆盆口半径为14寸,盆底半径为6寸,
则盆口面积为196π,盆底面积为36π,
又盆深18寸,盆中水深9寸,
则积水水面的半径为=10(寸),
∴积水水面面积为100π,
∴积水的体积V=×(36π++100π)×9=588π,
∴平地降雨量为=3(寸).]
13.πr2h
解析 依题意可得V=V圆柱-V圆锥
=πr2·h-·πr2·h=πr2h.
14.3∶1∶2
解析 设球的半径为R,则
V圆柱=πR2·2R=2πR3,
V圆锥=πR2·2R=πR3,
V球=πR3,
故V圆柱∶V圆锥∶V球
=2πR3∶πR3∶πR3
=3∶1∶2.
15.D [设圆柱底面半径为r,高为h,
则水的体积为πr2h.
水平放置后,水的体积为h,
所以πr2h=h,
整理得=θ-sin θ.]
16.解 (1)如图所示,将侧面展开,绳子的最短长度为侧面展开图中AM的长度,
设OB=l,∠AOA′=θ,
则θ·l=2π×5,
θ·(l+20)=2π×10,
解得θ=,l=20(cm).
∴OA=40(cm),OM=30(cm).
∴AM==50(cm).
即绳子的最短长度为50 cm.
(2)如图所示,作OQ⊥AM于点Q,交弧BB′于点P,
则PQ即为所求的最短距离.
∵OA·OM=AM·OQ,
∴OQ=24(cm).
故PQ=OQ-OP=24-20=4(cm),即上底圆周上的点到绳子的最短距离为4 cm.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
