实际问题与二次函数
图片预览




文档简介
课件26张PPT。2.3实际问题与二次函数湘教版九年级(下)梅桥中学九年级数学组 黄敏时,图象将发生怎样的变化?二次函数y=ax2y = a(x+d)2y = a(x+d)2 +h1、顶点坐标?(0,0)(–d,0)( –d,h )2、对称轴?y轴(直线x=0)(直线x= –d )(直线x= –d )3、平移问题?一般地,函数y=ax2的图象先向右(当d<0)或向左 (当d>0)平移|d|个单位可得y = a(x+d)2的图象;若再向上(当h>0 )或向下 (当h<0 )平移|h|个单位可得到y = a(x+d)2 +h的图象。
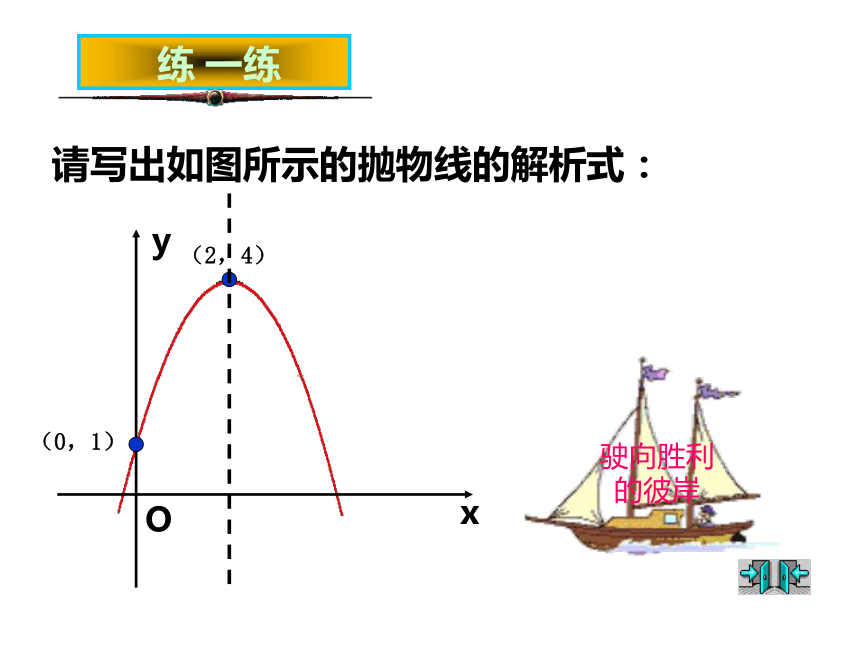
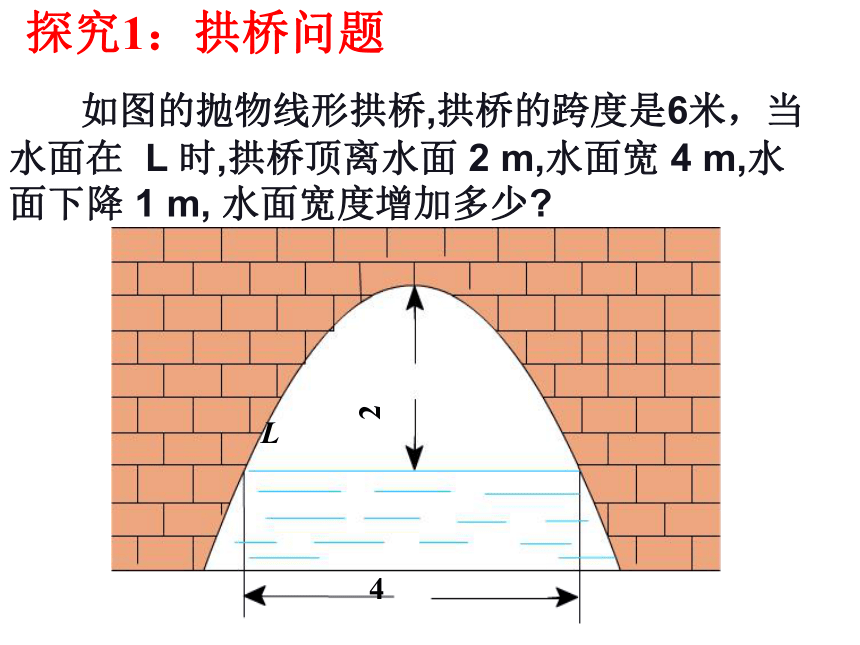
请写出如图所示的抛物线的解析式: (0,1)(2,4)xyO具有二次函数的图象抛物线的特征 如图的抛物线形拱桥,拱桥的跨度是6米,当水面在 L 时,拱桥顶离水面 2 m,水面宽 4 m,水面下降 1 m, 水面宽度增加多少?探究1:拱桥问题探究1: 如图的抛物线形拱桥,拱桥的跨度是6米,当水面在L 时,拱桥顶离水面 2 m,水面宽 4 m,水面下降 1 m, 水面宽度增加多少? 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度增加多少?0(2,-2)
●(-2,-2)
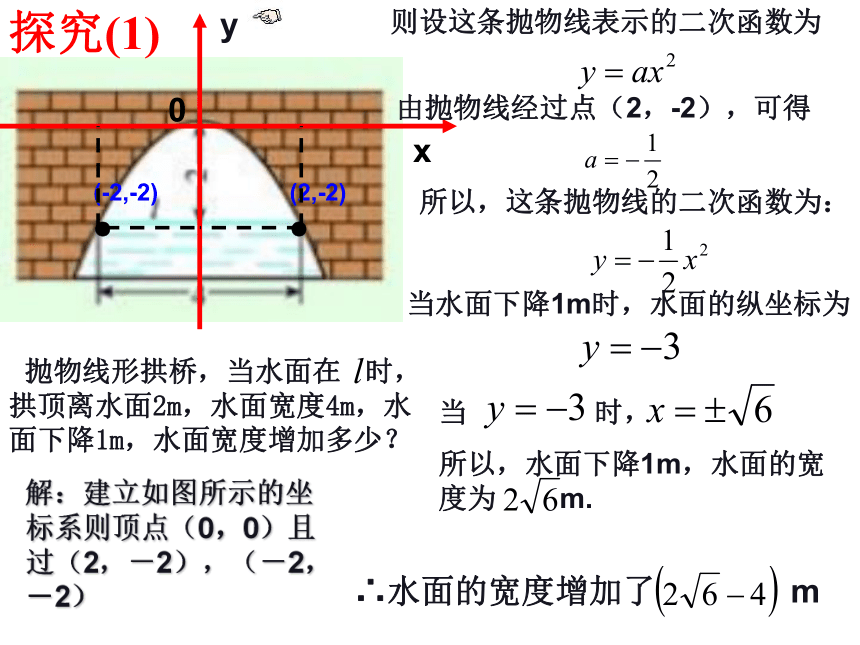
●探究(1)解:建立如图所示的坐标系则顶点(0,0)且过(2,-2),(-2,-2) 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度增加多少?0(4, 0)
●(0,0)
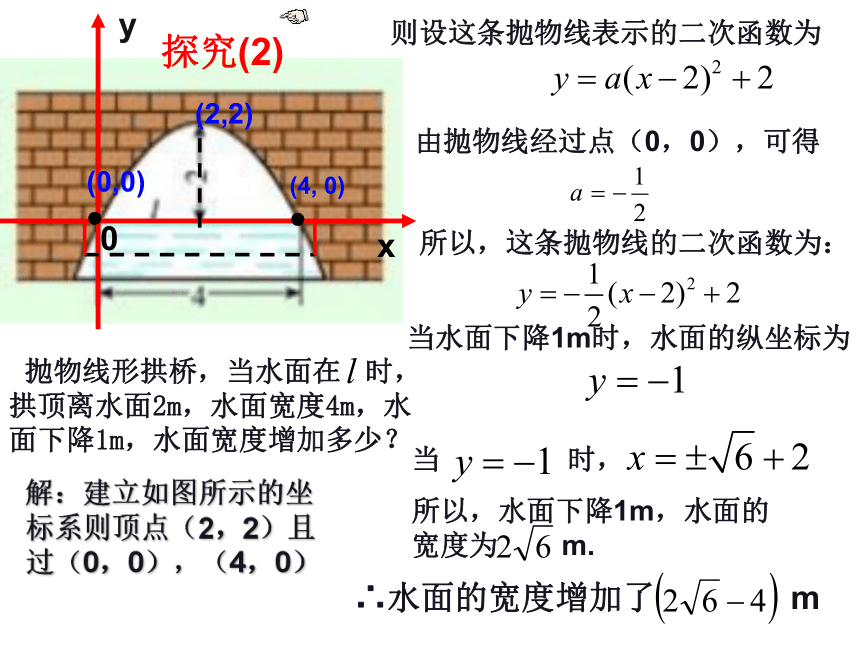
●(2,2)解:建立如图所示的坐标系则顶点(2,2)且过(0,0),(4,0)探究(2)变形题: 如图的抛物线形拱桥,拱桥的跨度是4.9米,当水面在L 时,拱桥顶离水面 2 m,水面宽 4 m,当水面宽3m时,拱桥顶离水面高多少 m?
一座拱桥的示意图如图,当水面宽4m时,桥洞顶部
离水面2m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究归纳:ABC2m4m 注意:
在解决实际问题时,我们应建立简单方便的平面直角坐标系. 用抛物线的知识解决生活中的一些实际问题的一般步骤:建立直角坐标系二次函数 问题求解 找出实际问题的答案总
结注意变量的取值范围例题1: 如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触上绳子,求绳子最低点到地面的距离。所以,绳子最低点到地面
的距离为 0.2米.解 :如图:以CD所在的直线为X轴,CD的中垂线为Y轴建立直角坐标系, 则 B(0.8, 2.2),F(- 0.4, 0.7)1m2.5m4m1m甲乙丙丁ABCD例题2: 你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地视为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
解:由题意,设抛物线解析式为 y =ax2+bx+1,
把 B(1,1.5),D(4,1)代入得:
把x=2.5代入得y=1.625∴C点的坐标为(2.5, 1.625)
∴丁的身高是1.625米 . y= -(x-1)2 +2.252.5练习:1.25探究2:投篮问题 一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米8米4米4米08(4,4)∵篮圈中心距离地面3米∴此球不能投中如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:3若假设出手的角度和力度都不变,
则如何才能使此球命中?(1)跳得高一点(2)向前平移一点探究延伸:(4,4)(8,3)在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?0 1 2 3 4 5 6 7 8 9 在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?(8,3)(5,4)(4,4)0 1 2 3 4 5 6 7 8 9(7,3)●解二次函数应用题的一般步骤:
1 . 审题,弄清已知和未知。
2 . 将实际问题转化为数学问题。建立适当的平面直角坐标系小结反思3 .根据题意找出点的坐标,求出抛物线 解析式。分析图象(并注意变量的取值范围), 解决实际问题。4 .返回实际背景检验。本节课你有哪些收获?你疑惑的地方有哪些?再 见
请写出如图所示的抛物线的解析式: (0,1)(2,4)xyO具有二次函数的图象抛物线的特征 如图的抛物线形拱桥,拱桥的跨度是6米,当水面在 L 时,拱桥顶离水面 2 m,水面宽 4 m,水面下降 1 m, 水面宽度增加多少?探究1:拱桥问题探究1: 如图的抛物线形拱桥,拱桥的跨度是6米,当水面在L 时,拱桥顶离水面 2 m,水面宽 4 m,水面下降 1 m, 水面宽度增加多少? 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度增加多少?0(2,-2)
●(-2,-2)
●探究(1)解:建立如图所示的坐标系则顶点(0,0)且过(2,-2),(-2,-2) 抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽度4m,水面下降1m,水面宽度增加多少?0(4, 0)
●(0,0)
●(2,2)解:建立如图所示的坐标系则顶点(2,2)且过(0,0),(4,0)探究(2)变形题: 如图的抛物线形拱桥,拱桥的跨度是4.9米,当水面在L 时,拱桥顶离水面 2 m,水面宽 4 m,当水面宽3m时,拱桥顶离水面高多少 m?
一座拱桥的示意图如图,当水面宽4m时,桥洞顶部
离水面2m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究归纳:ABC2m4m 注意:
在解决实际问题时,我们应建立简单方便的平面直角坐标系. 用抛物线的知识解决生活中的一些实际问题的一般步骤:建立直角坐标系二次函数 问题求解 找出实际问题的答案总
结注意变量的取值范围例题1: 如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触上绳子,求绳子最低点到地面的距离。所以,绳子最低点到地面
的距离为 0.2米.解 :如图:以CD所在的直线为X轴,CD的中垂线为Y轴建立直角坐标系, 则 B(0.8, 2.2),F(- 0.4, 0.7)1m2.5m4m1m甲乙丙丁ABCD例题2: 你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地视为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
解:由题意,设抛物线解析式为 y =ax2+bx+1,
把 B(1,1.5),D(4,1)代入得:
把x=2.5代入得y=1.625∴C点的坐标为(2.5, 1.625)
∴丁的身高是1.625米 . y= -(x-1)2 +2.252.5练习:1.25探究2:投篮问题 一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。 问此球能否投中?3米8米4米4米08(4,4)∵篮圈中心距离地面3米∴此球不能投中如图,建立平面 直角坐标系,点(4,4)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数为:3若假设出手的角度和力度都不变,
则如何才能使此球命中?(1)跳得高一点(2)向前平移一点探究延伸:(4,4)(8,3)在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?0 1 2 3 4 5 6 7 8 9 在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?(8,3)(5,4)(4,4)0 1 2 3 4 5 6 7 8 9(7,3)●解二次函数应用题的一般步骤:
1 . 审题,弄清已知和未知。
2 . 将实际问题转化为数学问题。建立适当的平面直角坐标系小结反思3 .根据题意找出点的坐标,求出抛物线 解析式。分析图象(并注意变量的取值范围), 解决实际问题。4 .返回实际背景检验。本节课你有哪些收获?你疑惑的地方有哪些?再 见
