同角的三角函数的基本关系
图片预览
文档简介
1.2.2同角的三角函数的基本关系
一:知识目标
1.理解同角的三角函数的基本关系
2.掌握同角的三角函数的基本关系的推导方法
3.会利用同角的三角函数的基本关系的求值化简与证明
二:能力目标
1.通过推导同角的三角函数的基本关系,体会数形结合的思想方法
2.通过应用同角的三角函数的基本关系,体会转化与化归的思想方法
三:教学重难点
1.重点:同角的三角函数的基本关系的推导与应用
2.难点:同角的三角函数的基本关系的几何推导
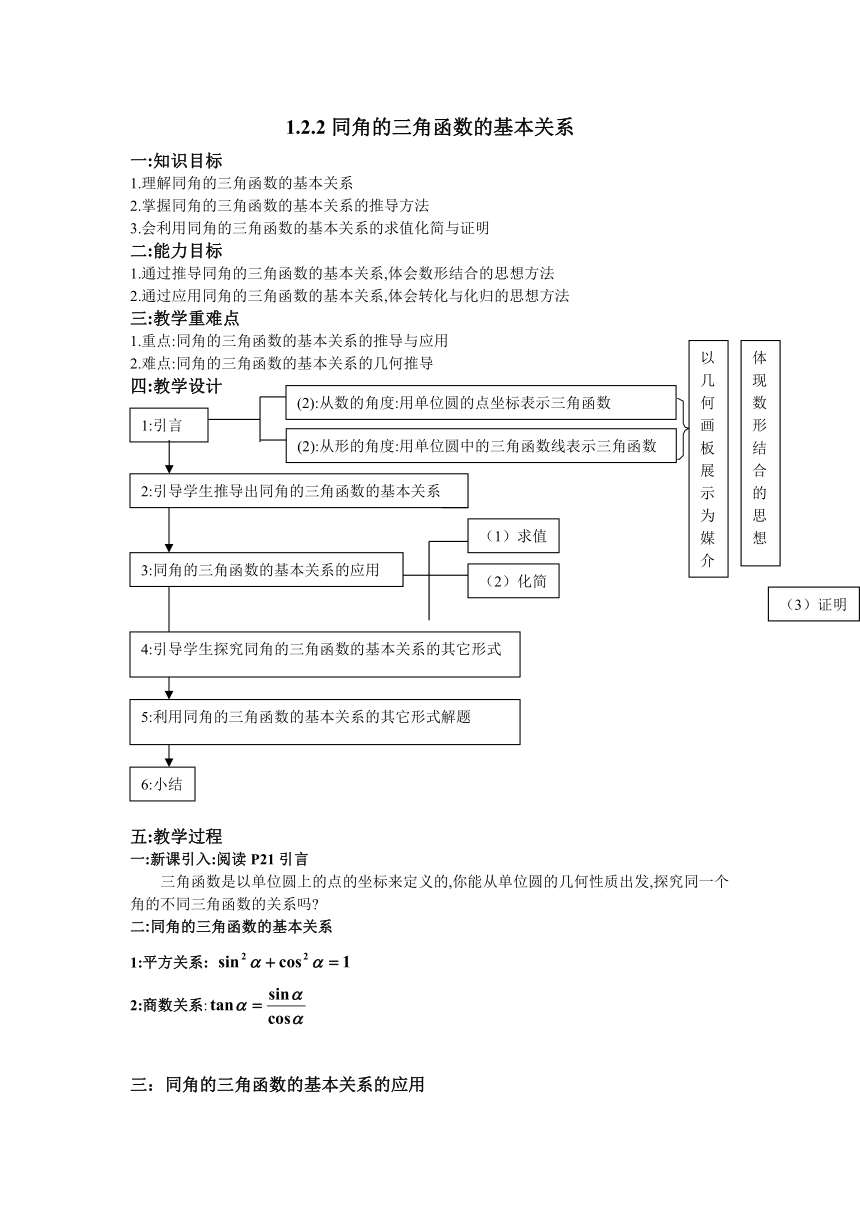
四:教学设计
五:教学过程
一:新课引入
:阅读P21引言
三角函数是以单位圆上的点的坐标来定义的,你能从单位圆的几何性质出发,探究同一个角的不同三角函数的关系吗
二:同角的三角函数的基本关系
1:平方关系:
2:商数关系:
三:同角的三角函数的基本关系的应用
1:应用之一:求三角函数值
2:应用之二:化简三角函数式
归纳:等式证明的思维路径
(1)变化等式的一边,直至与另一边相等
(2) 等式的两边分别变化,都等于第三式
(3)证明与原等式等价的等式成立
(1)
(2)
四:引导学生探究同角的三角函数的基本关系的其它形式
五:探究的应用
六:小结
(1) 求值(先定象限,后定值)
(2)
)
(1) 化简
(3)证明
2:高
以几何画板展示为媒介
体现数形结合的思想
(2):从数的角度:用单位圆的点坐标表示三角函数
1:引言
(2):从形的角度:用单位圆中的三角函数线表示三角函数
2:引导学生推导出同角的三角函数的基本关系
3:同角的三角函数的基本关系的应用
(3)证明
(2)化简
(1)求值
4:引导学生探究同角的三角函数的基本关系的其它形式
5:利用同角的三角函数的基本关系的其它形式解题
6:小结
平方关系
商数关系
(1):重视对“1”变形
(2):弦切互化
一:知识目标
1.理解同角的三角函数的基本关系
2.掌握同角的三角函数的基本关系的推导方法
3.会利用同角的三角函数的基本关系的求值化简与证明
二:能力目标
1.通过推导同角的三角函数的基本关系,体会数形结合的思想方法
2.通过应用同角的三角函数的基本关系,体会转化与化归的思想方法
三:教学重难点
1.重点:同角的三角函数的基本关系的推导与应用
2.难点:同角的三角函数的基本关系的几何推导
四:教学设计
五:教学过程
一:新课引入
:阅读P21引言
三角函数是以单位圆上的点的坐标来定义的,你能从单位圆的几何性质出发,探究同一个角的不同三角函数的关系吗
二:同角的三角函数的基本关系
1:平方关系:
2:商数关系:
三:同角的三角函数的基本关系的应用
1:应用之一:求三角函数值
2:应用之二:化简三角函数式
归纳:等式证明的思维路径
(1)变化等式的一边,直至与另一边相等
(2) 等式的两边分别变化,都等于第三式
(3)证明与原等式等价的等式成立
(1)
(2)
四:引导学生探究同角的三角函数的基本关系的其它形式
五:探究的应用
六:小结
(1) 求值(先定象限,后定值)
(2)
)
(1) 化简
(3)证明
2:高
以几何画板展示为媒介
体现数形结合的思想
(2):从数的角度:用单位圆的点坐标表示三角函数
1:引言
(2):从形的角度:用单位圆中的三角函数线表示三角函数
2:引导学生推导出同角的三角函数的基本关系
3:同角的三角函数的基本关系的应用
(3)证明
(2)化简
(1)求值
4:引导学生探究同角的三角函数的基本关系的其它形式
5:利用同角的三角函数的基本关系的其它形式解题
6:小结
平方关系
商数关系
(1):重视对“1”变形
(2):弦切互化
