第八章 §8.6 习题课 二面角的平面角的常见解法 课时练(含答案)
文档属性
| 名称 | 第八章 §8.6 习题课 二面角的平面角的常见解法 课时练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 343.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 11:54:55 | ||
图片预览




文档简介
习题课 二面角的平面角的常见解法
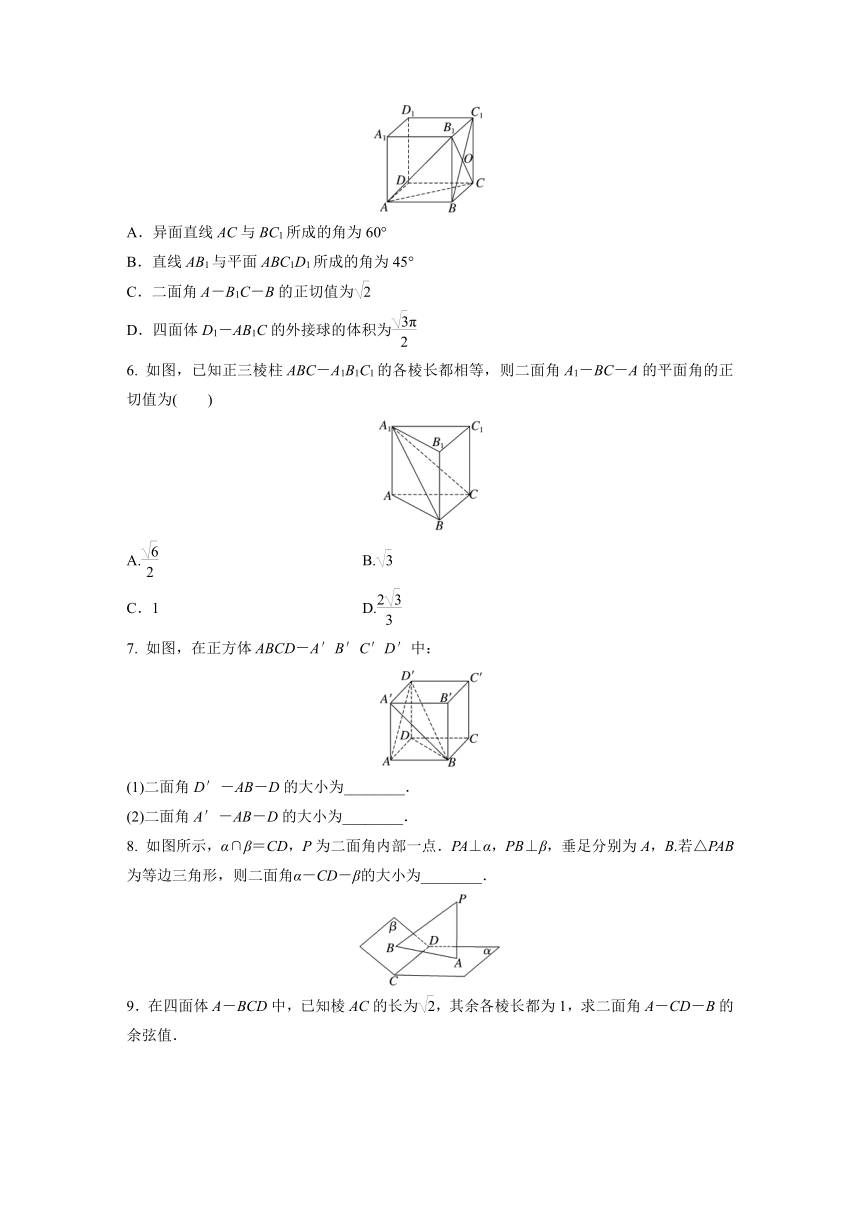
1. 如图,三棱台ABC-A1B1C1的下底面是正三角形,AB⊥BB1,B1C1⊥BB1,则二面角A-BB1-C的大小是( )
A.30° B.45°
C.60° D.90°
2.如图所示,将等腰Rt△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.则这个二面角的大小是( )
A.30° B.60°
C.90° D.120°
3.已知二面角α-l-β的大小为130°,两条异面直线a,b满足a α,b β,且a⊥l,b⊥l,则a,b所成角的大小为( )
A.40° B.50° C.130° D.140°
4. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱AD,BC的中点,则平面C1D1EF与底面ABCD所成的二面角的余弦值为( )
A. B. C. D.
5.(多选)如图,在棱长为1的正方体中,下列结论正确的是( )
A.异面直线AC与BC1所成的角为60°
B.直线AB1与平面ABC1D1所成的角为45°
C.二面角A-B1C-B的正切值为
D.四面体D1-AB1C的外接球的体积为
6. 如图,已知正三棱柱ABC-A1B1C1的各棱长都相等,则二面角A1-BC-A的平面角的正切值为( )
A. B.
C.1 D.
7. 如图,在正方体ABCD-A′B′C′D′中:
(1)二面角D′-AB-D的大小为________.
(2)二面角A′-AB-D的大小为________.
8. 如图所示,α∩β=CD,P为二面角内部一点.PA⊥α,PB⊥β,垂足分别为A,B.若△PAB为等边三角形,则二面角α-CD-β的大小为________.
9.在四面体A-BCD中,已知棱AC的长为,其余各棱长都为1,求二面角A-CD-B的余弦值.
10.在四棱锥P-ABCD中,四边形ABCD是平行四边形,PA⊥平面ABCD,PA=AB,∠ABC=30°,求二面角P-BC-A的余弦值.
11. 如图,将正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值为( )
A. B. C. D.
12.如图所示,在△ABC中,AD⊥BC,△ABD的面积是△ACD面积的2倍.沿AD将△ABC翻折,使翻折后BC⊥平面ACD,此时二面角B-AD-C的大小为( )
A.30° B.45° C.60° D.90°
13.二面角α-MN-β的平面角为θ1,AB α,B∈MN,∠ABM=θ2(θ2为锐角),AB与β的夹角为θ3,则下列关系式成立的是( )
A.cos θ3=cos θ1·cos θ2
B.cos θ3=sin θ1·cos θ2
C.sin θ3=sin θ1·sin θ2
D.sin θ3=cos θ1·sin θ2
14.将边长为1的正方形ABCD沿对角线AC折叠,使得点B和点D的距离为1,则二面角B-AC-D的大小为________.
15. “帷幄”是古代打仗必备的帐篷,又称“幄帐”.如图是一种幄帐示意图,帐顶采用“五脊四坡式”,四条斜脊的长度相等,一条正脊平行于底面,若各斜坡面与底面所成二面角的正切值均为,底面矩形的长与宽之比为2∶1,则正脊与斜脊长度的比值为( )
A. B.2 C. D.
16. 如图,在水平放置的直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=DC=AB=1,以AB所在直线为轴,将梯形ABCD向上旋转角θ得到梯形ABEF,其中θ∈.
(1)证明:平面ADF⊥平面CDFE;
(2)若平面ADF与平面BCE所成的二面角的余弦值等于,求θ的值.
习题课 二面角的平面角的常见解法
1.C 2.C 3.B 4.B
5.ACD [如图所示,连接AD1,AO,CD1,
对于A,易知BC1∥AD1,则∠D1AC为异面直线AC与BC1所成的角,显然△AD1C为正三角形,
∴∠D1AC=60°,故A正确;
对于B,∵B1O⊥BC1,B1O⊥AB,AB∩BC1=B,∴B1O⊥平面ABC1D1,∴∠B1AO为直线AB1与平面ABC1D1所成的角,
∵AO=,B1O=,
∴tan∠B1AO==,
∴∠B1AO=30°,故B错误;
对于C,在△AB1C中,AO⊥B1C,
∴∠AOB为二面角A-B1C-B的平面角,tan∠AOB===,故C正确;
对于D,利用补形法可知三棱锥的外接球即为正方体的外接球,∴R=,∴V=R3=,故D正确.]
6.D [设棱长为a,BC的中点为E,连接A1E,AE(图略),由正三棱柱ABC-A1B1C1的各棱长都相等,可得A1E⊥BC,AE⊥BC,所以二面角A1-BC-A的平面角为∠A1EA,在等边△ABC中,AE=a,
所以tan∠A1EA=
==,
即二面角A1-BC-A的平面角的正切值为.]
7.(1)45° (2)90°
8.120°
解析 设平面PAB与棱CD交于点E,
如图,连接BE,AE,易得CD⊥BE,CD⊥AE,
则∠BEA即为所求二面角的平面角.
∵△PAB为等边三角形,
∴∠APB=60°,∴∠BEA=120°.
故二面角α-CD-β的大小为120°.
9.解 如图,由已知可得AD⊥DC,
又由其余各棱长都为1,得△BCD为等边三角形,取CD的中点E,连接BE,则BE⊥CD,
在平面ADC中,过E作AD的平行线交AC于点F,连接BF,则EF⊥CD,则∠BEF为二面角A-CD-B的平面角.
∵EF=,BE=,BF=,
∴cos∠BEF=
==.
10.解 设PA=AB=2,过点A在平面ABCD内作AE⊥BC交BC于点E,连接PE,如图所示,
∵PA⊥平面ABCD,BC 平面ABCD,
∴BC⊥PA,
∵AE⊥BC,PA∩AE=A,PA,AE 平面PAE,
∴BC⊥平面PAE,
∵PE 平面PAE,∴PE⊥BC,
∴二面角P-BC-A的平面角为∠PEA,
在Rt△ABE中,∠AEB=90°,∠ABE=30°,
AB=2,
则AE=AB=1,
∵PA⊥平面ABCD,AE 平面ABCD,
∴PA⊥AE,
∴PE==,
∴cos∠PEA===.
∴二面角P-BC-A的余弦值为.
11.B [∵以正方形A1BCD的对角线BD为棱折成直二面角,
∴平面ABD⊥平面BCD,连接A1C交BD于点O,连接AO,如图所示,
则AO⊥BD,
∵平面ABD∩平面BCD=BD,AO 平面ABD,
∴AO⊥平面BCD,
∴AO⊥CD,
取CD的中点M,连接OM,AM,
则OM∥BC,
∴OM⊥CD,
又AO∩OM=O,
∴CD⊥平面AOM,
∴AM⊥CD,
∴∠AMO即为二面角A-CD-B的平面角.
设正方形A1BCD的边长为2,
则AO=,OM=1,
∴AM==.
∴cos∠AMO===.]
12.C [由已知得BD=2CD.翻折后,易知BC⊥CD.在Rt△BCD中,∠BDC=60°.而AD⊥BD,CD⊥AD,故∠BDC是二面角B-AD-C的平面角,其大小为60°.]
13.C [如图,过点A作AH⊥β于点H,作HO⊥MN于点O,连接AO,则AO⊥MN,所以∠AOH为α-MN-β的平面角,∠ABH为AB与β所成的角,因为sin θ1=,sin θ2=,
所以sin θ1·sin θ2=·==sin θ3.]
14.
解析 设翻折前AC与BD相交于点O,
则OB⊥AC,OD⊥AC,而翻折之后的图形如图所示,
∴∠BOD为二面角B-AC-D的平面角,
∵OB=OD=,BD=1,
∴△BOD为等腰直角三角形,且∠BOD=,
∴二面角B-AC-D的大小为.
15.A [设正脊长为a,斜脊长为b,底面矩形的长与宽分别为2t和t,
如图,过S作SO⊥上底平面于O,过O作OE⊥AD于E,作OF⊥AB于F,
连接SE,SF,OA,
由题意知
tan∠SEO=tan∠SFO=,
SE2=SA2-AE2=b2-2,
SF2=SB2-BF2=b2-2,
所以=,于是a=t,
SA=b=
==,
所以==.]
16.(1)证明 由题意,知AB⊥AD,AB⊥AF,AD∩AF=A,且AD,AF 平面ADF,
所以AB⊥平面ADF,
又AB∥CD,
所以CD⊥平面ADF,
因为CD 平面CDFE,
所以平面ADF⊥平面CDFE.
(2)解 因为EF∥AB∥CD,
所以EF⊥平面ADF,
从而△BCE在平面ADF内的投影为△ADF,
所以平面ADF与平面BCE所成二面角的余弦值为,
由已知得∠FAD=θ,AF=AD=1,BE=BC=,FD=EC=2sin ,
所以S△ADF=sin θ=sin cos ,
S△BCE=·2sin ·=sin ·,
从而=
==,
即cos2=,
因为θ∈,
所以cos >0,所以cos =,
所以=,
故θ=.
1. 如图,三棱台ABC-A1B1C1的下底面是正三角形,AB⊥BB1,B1C1⊥BB1,则二面角A-BB1-C的大小是( )
A.30° B.45°
C.60° D.90°
2.如图所示,将等腰Rt△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.则这个二面角的大小是( )
A.30° B.60°
C.90° D.120°
3.已知二面角α-l-β的大小为130°,两条异面直线a,b满足a α,b β,且a⊥l,b⊥l,则a,b所成角的大小为( )
A.40° B.50° C.130° D.140°
4. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱AD,BC的中点,则平面C1D1EF与底面ABCD所成的二面角的余弦值为( )
A. B. C. D.
5.(多选)如图,在棱长为1的正方体中,下列结论正确的是( )
A.异面直线AC与BC1所成的角为60°
B.直线AB1与平面ABC1D1所成的角为45°
C.二面角A-B1C-B的正切值为
D.四面体D1-AB1C的外接球的体积为
6. 如图,已知正三棱柱ABC-A1B1C1的各棱长都相等,则二面角A1-BC-A的平面角的正切值为( )
A. B.
C.1 D.
7. 如图,在正方体ABCD-A′B′C′D′中:
(1)二面角D′-AB-D的大小为________.
(2)二面角A′-AB-D的大小为________.
8. 如图所示,α∩β=CD,P为二面角内部一点.PA⊥α,PB⊥β,垂足分别为A,B.若△PAB为等边三角形,则二面角α-CD-β的大小为________.
9.在四面体A-BCD中,已知棱AC的长为,其余各棱长都为1,求二面角A-CD-B的余弦值.
10.在四棱锥P-ABCD中,四边形ABCD是平行四边形,PA⊥平面ABCD,PA=AB,∠ABC=30°,求二面角P-BC-A的余弦值.
11. 如图,将正方形A1BCD折成直二面角A-BD-C,则二面角A-CD-B的余弦值为( )
A. B. C. D.
12.如图所示,在△ABC中,AD⊥BC,△ABD的面积是△ACD面积的2倍.沿AD将△ABC翻折,使翻折后BC⊥平面ACD,此时二面角B-AD-C的大小为( )
A.30° B.45° C.60° D.90°
13.二面角α-MN-β的平面角为θ1,AB α,B∈MN,∠ABM=θ2(θ2为锐角),AB与β的夹角为θ3,则下列关系式成立的是( )
A.cos θ3=cos θ1·cos θ2
B.cos θ3=sin θ1·cos θ2
C.sin θ3=sin θ1·sin θ2
D.sin θ3=cos θ1·sin θ2
14.将边长为1的正方形ABCD沿对角线AC折叠,使得点B和点D的距离为1,则二面角B-AC-D的大小为________.
15. “帷幄”是古代打仗必备的帐篷,又称“幄帐”.如图是一种幄帐示意图,帐顶采用“五脊四坡式”,四条斜脊的长度相等,一条正脊平行于底面,若各斜坡面与底面所成二面角的正切值均为,底面矩形的长与宽之比为2∶1,则正脊与斜脊长度的比值为( )
A. B.2 C. D.
16. 如图,在水平放置的直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=DC=AB=1,以AB所在直线为轴,将梯形ABCD向上旋转角θ得到梯形ABEF,其中θ∈.
(1)证明:平面ADF⊥平面CDFE;
(2)若平面ADF与平面BCE所成的二面角的余弦值等于,求θ的值.
习题课 二面角的平面角的常见解法
1.C 2.C 3.B 4.B
5.ACD [如图所示,连接AD1,AO,CD1,
对于A,易知BC1∥AD1,则∠D1AC为异面直线AC与BC1所成的角,显然△AD1C为正三角形,
∴∠D1AC=60°,故A正确;
对于B,∵B1O⊥BC1,B1O⊥AB,AB∩BC1=B,∴B1O⊥平面ABC1D1,∴∠B1AO为直线AB1与平面ABC1D1所成的角,
∵AO=,B1O=,
∴tan∠B1AO==,
∴∠B1AO=30°,故B错误;
对于C,在△AB1C中,AO⊥B1C,
∴∠AOB为二面角A-B1C-B的平面角,tan∠AOB===,故C正确;
对于D,利用补形法可知三棱锥的外接球即为正方体的外接球,∴R=,∴V=R3=,故D正确.]
6.D [设棱长为a,BC的中点为E,连接A1E,AE(图略),由正三棱柱ABC-A1B1C1的各棱长都相等,可得A1E⊥BC,AE⊥BC,所以二面角A1-BC-A的平面角为∠A1EA,在等边△ABC中,AE=a,
所以tan∠A1EA=
==,
即二面角A1-BC-A的平面角的正切值为.]
7.(1)45° (2)90°
8.120°
解析 设平面PAB与棱CD交于点E,
如图,连接BE,AE,易得CD⊥BE,CD⊥AE,
则∠BEA即为所求二面角的平面角.
∵△PAB为等边三角形,
∴∠APB=60°,∴∠BEA=120°.
故二面角α-CD-β的大小为120°.
9.解 如图,由已知可得AD⊥DC,
又由其余各棱长都为1,得△BCD为等边三角形,取CD的中点E,连接BE,则BE⊥CD,
在平面ADC中,过E作AD的平行线交AC于点F,连接BF,则EF⊥CD,则∠BEF为二面角A-CD-B的平面角.
∵EF=,BE=,BF=,
∴cos∠BEF=
==.
10.解 设PA=AB=2,过点A在平面ABCD内作AE⊥BC交BC于点E,连接PE,如图所示,
∵PA⊥平面ABCD,BC 平面ABCD,
∴BC⊥PA,
∵AE⊥BC,PA∩AE=A,PA,AE 平面PAE,
∴BC⊥平面PAE,
∵PE 平面PAE,∴PE⊥BC,
∴二面角P-BC-A的平面角为∠PEA,
在Rt△ABE中,∠AEB=90°,∠ABE=30°,
AB=2,
则AE=AB=1,
∵PA⊥平面ABCD,AE 平面ABCD,
∴PA⊥AE,
∴PE==,
∴cos∠PEA===.
∴二面角P-BC-A的余弦值为.
11.B [∵以正方形A1BCD的对角线BD为棱折成直二面角,
∴平面ABD⊥平面BCD,连接A1C交BD于点O,连接AO,如图所示,
则AO⊥BD,
∵平面ABD∩平面BCD=BD,AO 平面ABD,
∴AO⊥平面BCD,
∴AO⊥CD,
取CD的中点M,连接OM,AM,
则OM∥BC,
∴OM⊥CD,
又AO∩OM=O,
∴CD⊥平面AOM,
∴AM⊥CD,
∴∠AMO即为二面角A-CD-B的平面角.
设正方形A1BCD的边长为2,
则AO=,OM=1,
∴AM==.
∴cos∠AMO===.]
12.C [由已知得BD=2CD.翻折后,易知BC⊥CD.在Rt△BCD中,∠BDC=60°.而AD⊥BD,CD⊥AD,故∠BDC是二面角B-AD-C的平面角,其大小为60°.]
13.C [如图,过点A作AH⊥β于点H,作HO⊥MN于点O,连接AO,则AO⊥MN,所以∠AOH为α-MN-β的平面角,∠ABH为AB与β所成的角,因为sin θ1=,sin θ2=,
所以sin θ1·sin θ2=·==sin θ3.]
14.
解析 设翻折前AC与BD相交于点O,
则OB⊥AC,OD⊥AC,而翻折之后的图形如图所示,
∴∠BOD为二面角B-AC-D的平面角,
∵OB=OD=,BD=1,
∴△BOD为等腰直角三角形,且∠BOD=,
∴二面角B-AC-D的大小为.
15.A [设正脊长为a,斜脊长为b,底面矩形的长与宽分别为2t和t,
如图,过S作SO⊥上底平面于O,过O作OE⊥AD于E,作OF⊥AB于F,
连接SE,SF,OA,
由题意知
tan∠SEO=tan∠SFO=,
SE2=SA2-AE2=b2-2,
SF2=SB2-BF2=b2-2,
所以=,于是a=t,
SA=b=
==,
所以==.]
16.(1)证明 由题意,知AB⊥AD,AB⊥AF,AD∩AF=A,且AD,AF 平面ADF,
所以AB⊥平面ADF,
又AB∥CD,
所以CD⊥平面ADF,
因为CD 平面CDFE,
所以平面ADF⊥平面CDFE.
(2)解 因为EF∥AB∥CD,
所以EF⊥平面ADF,
从而△BCE在平面ADF内的投影为△ADF,
所以平面ADF与平面BCE所成二面角的余弦值为,
由已知得∠FAD=θ,AF=AD=1,BE=BC=,FD=EC=2sin ,
所以S△ADF=sin θ=sin cos ,
S△BCE=·2sin ·=sin ·,
从而=
==,
即cos2=,
因为θ∈,
所以cos >0,所以cos =,
所以=,
故θ=.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
