第八章 §8.6 习题课 异面直线所成的角及直线与平面所成的角的解法 课时练(含答案)
文档属性
| 名称 | 第八章 §8.6 习题课 异面直线所成的角及直线与平面所成的角的解法 课时练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 398.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 13:01:12 | ||
图片预览


文档简介
习题课 异面直线所成的角及直线与平面所成的角的解法
1.在正方体ABCD-A1B1C1D1中,直线AC1与CD所成角的余弦值为( )
A. B. C. D.
2.在正方体ABCD-A1B1C1D1中,E,F分别是棱AA1,AB的中点,则异面直线EF与C1D所成角的大小是( )
A. B. C. D.
3.已知圆锥SO的底面半径为r,当圆锥的体积为πr3时,该圆锥的母线与底面所成角的正弦值为( )
A. B. C. D.
4.若斜线段AB的长是它在平面α上的射影长的2倍,则AB与平面α所成的角是( )
A.60° B.45° C.30° D.120°
5.在正方体ABCD-A1B1C1D1中,BB1和平面ACD1所成角的余弦值为( )
A. B. C. D.
6. 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,则平面AD1E与平面ABCD的交线与直线C1D1所成角的正切值为( )
A. B. C. D.2
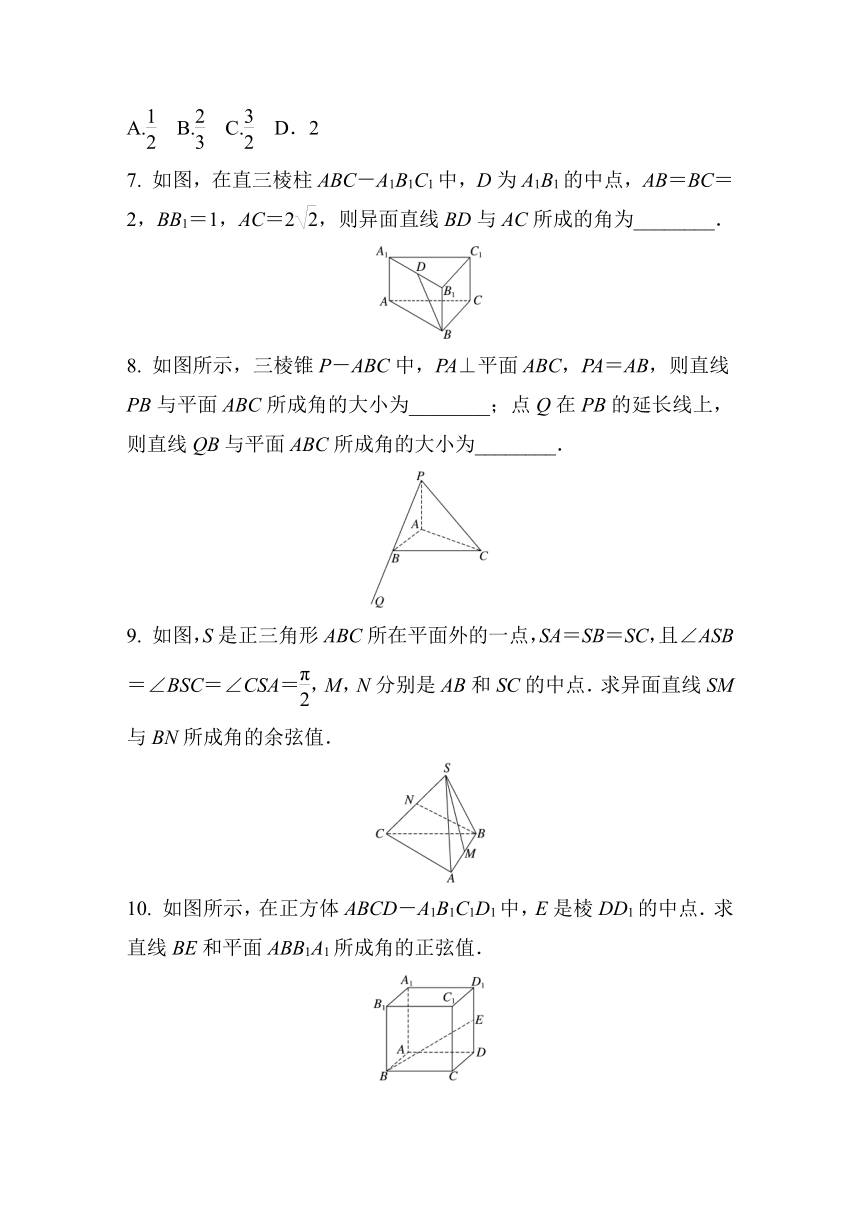
7. 如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=2,BB1=1,AC=2,则异面直线BD与AC所成的角为________.
8. 如图所示,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的大小为________;点Q在PB的延长线上,则直线QB与平面ABC所成角的大小为________.
9. 如图,S是正三角形ABC所在平面外的一点,SA=SB=SC,且∠ASB=∠BSC=∠CSA=,M,N分别是AB和SC的中点.求异面直线SM与BN所成角的余弦值.
10. 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.求直线BE和平面ABB1A1所成角的正弦值.
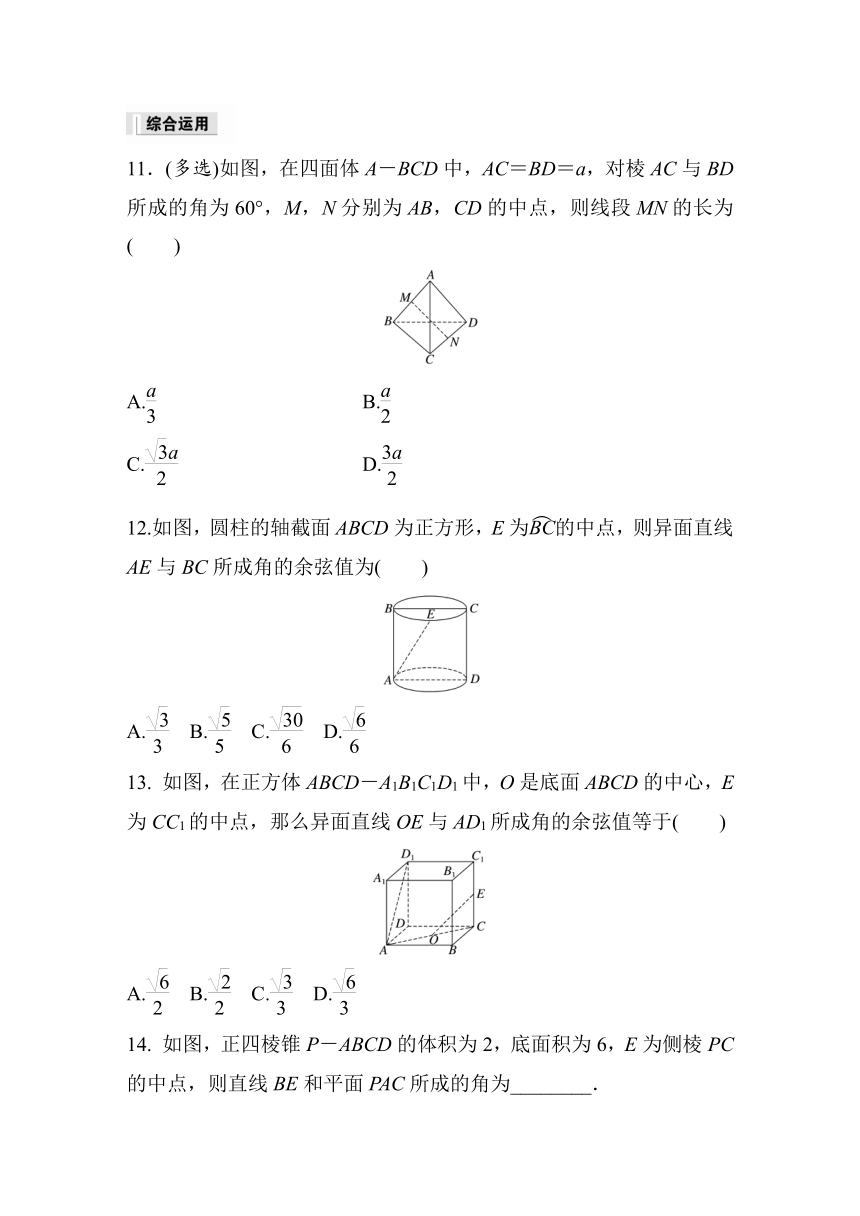
11.(多选)如图,在四面体A-BCD中,AC=BD=a,对棱AC与BD所成的角为60°,M,N分别为AB,CD的中点,则线段MN的长为( )
A. B.
C. D.
12.如图,圆柱的轴截面ABCD为正方形,E为的中点,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
13. 如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于( )
A. B. C. D.
14. 如图,正四棱锥P-ABCD的体积为2,底面积为6,E为侧棱PC的中点,则直线BE和平面PAC所成的角为________.
15.(多选)《九章算术》卷五《商功》中描述几何体“阳马”为底面为矩形,一棱垂直于底面的四棱锥,如图,在直角梯形ABCS中,∠ABC=∠BCS=90°,SC=2BC=2AB=2,过点A作AD⊥SC交SC于点D,以AD为折痕把△SAD折起,当几何体S-ABCD为阳马时,下列四个命题正确的是( )
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成角的大小等于45°
D.AB与SC所成角的大小等于30°
16. 如图,点P为平面ABC外一点,AP,AB,AC两两互相垂直,过AC的中点D作ED⊥平面ABC,且ED=1,PA=2,AC=2,连接BP,BE,BD,多面体B-PADE的体积是.
(1)画出平面PBE与平面ABC的交线,并说明理由;
(2)求BE和平面PADE所成角的正切值.
习题课 异面直线所成的角及直线与平面所成的角的解法
1.B 2.D 3.A 4.A
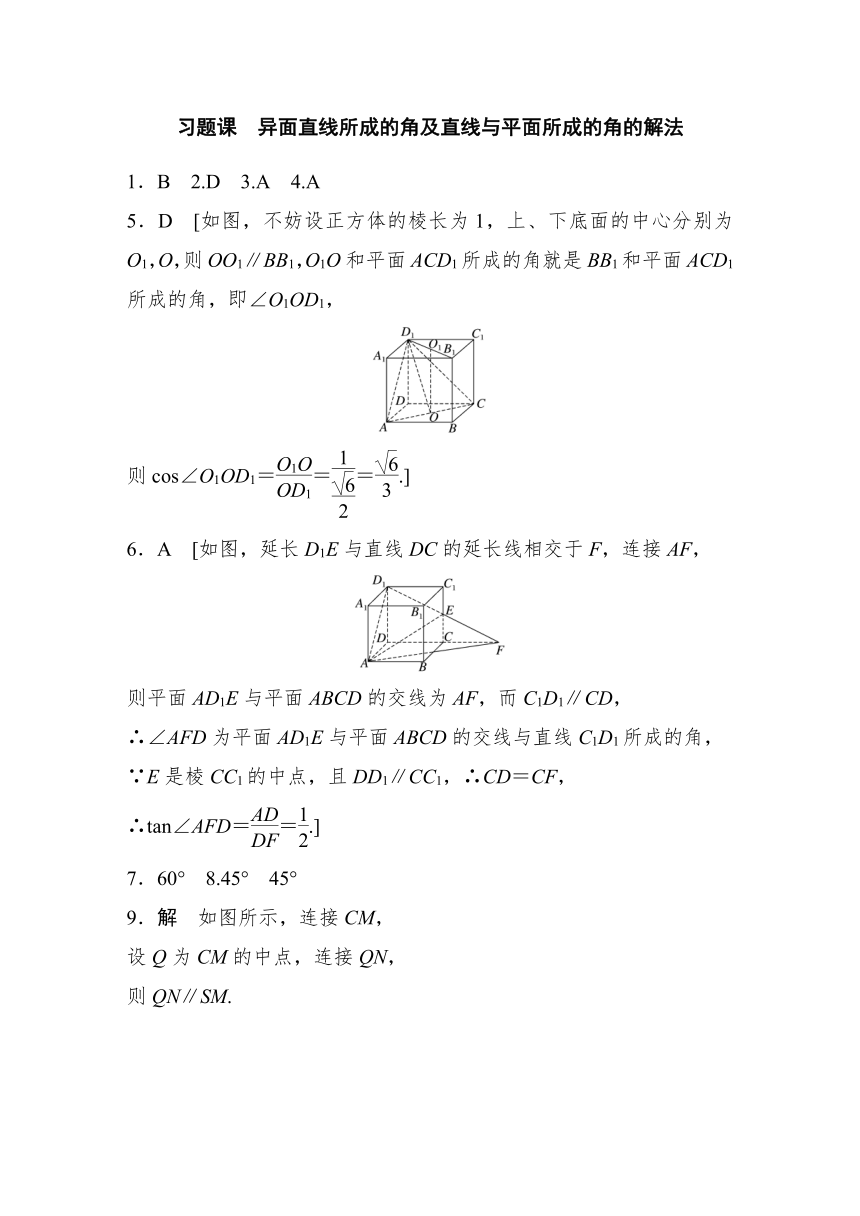
5.D [如图,不妨设正方体的棱长为1,上、下底面的中心分别为O1,O,则OO1∥BB1,O1O和平面ACD1所成的角就是BB1和平面ACD1所成的角,即∠O1OD1,
则cos∠O1OD1===.]
6.A [如图,延长D1E与直线DC的延长线相交于F,连接AF,
则平面AD1E与平面ABCD的交线为AF,而C1D1∥CD,
∴∠AFD为平面AD1E与平面ABCD的交线与直线C1D1所成的角,
∵E是棱CC1的中点,且DD1∥CC1,∴CD=CF,
∴tan∠AFD==.]
7.60° 8.45° 45°
9.解 如图所示,连接CM,
设Q为CM的中点,连接QN,
则QN∥SM.
∴∠QNB或其补角是异面直线SM与BN所成的角.
连接BQ,设SC=a,在△BQN中,
BN=a,NQ=SM=a,BQ=a,
∴cos∠QNB=
==.
即异面直线SM与BN所成角的余弦值为.
10.解 如图,取AA1的中点M,连接EM,BM.
因为E是DD1的中点,四边形ADD1A1为正方形,
所以EM∥AD.
又在正方体ABCD-A1B1C1D1中,
AD⊥平面ABB1A1,所以EM⊥平面ABB1A1,
从而直线BM为直线BE在平面ABB1A1上的射影,
∠EBM即为直线BE和平面ABB1A1所成的角.
设正方体的棱长为2a,
则EM=AD=2a,
BE==3a.
于是在Rt△BEM中,
sin∠EBM==,
即直线BE和平面ABB1A1所成角的正弦值为.
11.BC [取BC的中点E,连接EN,EM,如图所示.
因为M为AB的中点,
所以ME∥AC,且ME=AC=,
同理得EN∥BD,且EN=,
所以∠MEN或其补角为异面直线AC与BD所成的角,
在△MEN中,EM=EN,若∠MEN=60°,
则△MEN为等边三角形,
所以MN=.
若∠MEN=120°,可得MN=.]
12.D [如图,取BC的中点H,连接EH,AH,则∠EHA=90°.设AB=2,则BH=HE=1,AH=,所以AE=.连接ED,则ED=.因为BC∥AD,所以异面直线AE与BC所成的角即为∠EAD(或其补角).在△EAD中,cos∠EAD=
==.]
13.D [如图所示,取BC的中点F,连接EF,OF,BC1.
因为E为CC1的中点,
所以EF∥BC1∥AD1,
故∠OEF或其补角即为异面直线OE与AD1所成的角,
设正方体ABCD-A1B1C1D1的棱长为2,
则在△OEF中,EF=,OE=,OF=1,
故∠OFE=90°,故cos∠OEF===.]
14.60°
解析 如图,在正四棱锥P-ABCD中,连接BD,交AC于点O,连接PO,
则PO⊥平面ABCD,在正四棱锥中,BO⊥平面PAC.
连接OE,DE,则∠BEO是直线BE和平面PAC所成的角.
∵正四棱锥P-ABCD的体积为2,底面积为6,
∴V=×6×PO=2,则PO=1,
BC=,则OC=OB=,
∵E为侧棱PC的中点,
∴取OC的中点H,连接EH,
则EH⊥OC,
EH=PO=,OH=OC=,
则OE=
==1.
在Rt△BOE中,
tan∠BEO===,
则∠BEO=60°.
15.AB [如图,当几何体S-ABCD为阳马时,SD⊥平面ABCD,
对于A,SD⊥平面ABCD,所以AC⊥SD,又AC⊥BD,SD∩BD=D,
故AC⊥平面SBD,所以AC⊥SB,故A正确;
对于B,因为AB∥CD,且AB 平面SCD,CD 平面SCD,故AB∥平面SCD,故B正确;
对于C,由A知,AC⊥平面SBD,连接SO,则∠ASO是SA与平面SBD所成的角,
因为SA=,OA=,
所以∠ASO=30°,故C不正确;
对于D,因为AB∥CD,所以∠SCD是AB与SC所成的角,因为SD=CD=1,所以∠SCD=45°,故D不正确.]
16.解 (1)如图,延长PE交AC于点F,连接BF,
∵AP,AB,AC两两互相垂直,
∴PA⊥平面ABC.
∵DE⊥平面ABC,
∴DE∥PA,
∴==,
∴F与C重合.
∵C∈PE,C∈AC,PE 平面PBE,AC 平面ABC,
∴C是平面PBE与平面ABC的公共点.
又B是平面PBE与平面ABC的公共点,
∴BC是平面PBE与平面ABC的交线.
(2)如图,连接AE.
∵AP,AB,AC两两互相垂直,
∴AB⊥平面PAC,
∴∠BEA为BE和平面PADE所成的角.
∵VB-PADE=S梯形ADEP·AB
=××(1+2)×1×AB=,
∴AB=.
又∵AE==,
∴tan∠BEA===,
所以BE和平面PADE所成角的正切值为.
1.在正方体ABCD-A1B1C1D1中,直线AC1与CD所成角的余弦值为( )
A. B. C. D.
2.在正方体ABCD-A1B1C1D1中,E,F分别是棱AA1,AB的中点,则异面直线EF与C1D所成角的大小是( )
A. B. C. D.
3.已知圆锥SO的底面半径为r,当圆锥的体积为πr3时,该圆锥的母线与底面所成角的正弦值为( )
A. B. C. D.
4.若斜线段AB的长是它在平面α上的射影长的2倍,则AB与平面α所成的角是( )
A.60° B.45° C.30° D.120°
5.在正方体ABCD-A1B1C1D1中,BB1和平面ACD1所成角的余弦值为( )
A. B. C. D.
6. 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,则平面AD1E与平面ABCD的交线与直线C1D1所成角的正切值为( )
A. B. C. D.2
7. 如图,在直三棱柱ABC-A1B1C1中,D为A1B1的中点,AB=BC=2,BB1=1,AC=2,则异面直线BD与AC所成的角为________.
8. 如图所示,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的大小为________;点Q在PB的延长线上,则直线QB与平面ABC所成角的大小为________.
9. 如图,S是正三角形ABC所在平面外的一点,SA=SB=SC,且∠ASB=∠BSC=∠CSA=,M,N分别是AB和SC的中点.求异面直线SM与BN所成角的余弦值.
10. 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.求直线BE和平面ABB1A1所成角的正弦值.
11.(多选)如图,在四面体A-BCD中,AC=BD=a,对棱AC与BD所成的角为60°,M,N分别为AB,CD的中点,则线段MN的长为( )
A. B.
C. D.
12.如图,圆柱的轴截面ABCD为正方形,E为的中点,则异面直线AE与BC所成角的余弦值为( )
A. B. C. D.
13. 如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于( )
A. B. C. D.
14. 如图,正四棱锥P-ABCD的体积为2,底面积为6,E为侧棱PC的中点,则直线BE和平面PAC所成的角为________.
15.(多选)《九章算术》卷五《商功》中描述几何体“阳马”为底面为矩形,一棱垂直于底面的四棱锥,如图,在直角梯形ABCS中,∠ABC=∠BCS=90°,SC=2BC=2AB=2,过点A作AD⊥SC交SC于点D,以AD为折痕把△SAD折起,当几何体S-ABCD为阳马时,下列四个命题正确的是( )
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成角的大小等于45°
D.AB与SC所成角的大小等于30°
16. 如图,点P为平面ABC外一点,AP,AB,AC两两互相垂直,过AC的中点D作ED⊥平面ABC,且ED=1,PA=2,AC=2,连接BP,BE,BD,多面体B-PADE的体积是.
(1)画出平面PBE与平面ABC的交线,并说明理由;
(2)求BE和平面PADE所成角的正切值.
习题课 异面直线所成的角及直线与平面所成的角的解法
1.B 2.D 3.A 4.A
5.D [如图,不妨设正方体的棱长为1,上、下底面的中心分别为O1,O,则OO1∥BB1,O1O和平面ACD1所成的角就是BB1和平面ACD1所成的角,即∠O1OD1,
则cos∠O1OD1===.]
6.A [如图,延长D1E与直线DC的延长线相交于F,连接AF,
则平面AD1E与平面ABCD的交线为AF,而C1D1∥CD,
∴∠AFD为平面AD1E与平面ABCD的交线与直线C1D1所成的角,
∵E是棱CC1的中点,且DD1∥CC1,∴CD=CF,
∴tan∠AFD==.]
7.60° 8.45° 45°
9.解 如图所示,连接CM,
设Q为CM的中点,连接QN,
则QN∥SM.
∴∠QNB或其补角是异面直线SM与BN所成的角.
连接BQ,设SC=a,在△BQN中,
BN=a,NQ=SM=a,BQ=a,
∴cos∠QNB=
==.
即异面直线SM与BN所成角的余弦值为.
10.解 如图,取AA1的中点M,连接EM,BM.
因为E是DD1的中点,四边形ADD1A1为正方形,
所以EM∥AD.
又在正方体ABCD-A1B1C1D1中,
AD⊥平面ABB1A1,所以EM⊥平面ABB1A1,
从而直线BM为直线BE在平面ABB1A1上的射影,
∠EBM即为直线BE和平面ABB1A1所成的角.
设正方体的棱长为2a,
则EM=AD=2a,
BE==3a.
于是在Rt△BEM中,
sin∠EBM==,
即直线BE和平面ABB1A1所成角的正弦值为.
11.BC [取BC的中点E,连接EN,EM,如图所示.
因为M为AB的中点,
所以ME∥AC,且ME=AC=,
同理得EN∥BD,且EN=,
所以∠MEN或其补角为异面直线AC与BD所成的角,
在△MEN中,EM=EN,若∠MEN=60°,
则△MEN为等边三角形,
所以MN=.
若∠MEN=120°,可得MN=.]
12.D [如图,取BC的中点H,连接EH,AH,则∠EHA=90°.设AB=2,则BH=HE=1,AH=,所以AE=.连接ED,则ED=.因为BC∥AD,所以异面直线AE与BC所成的角即为∠EAD(或其补角).在△EAD中,cos∠EAD=
==.]
13.D [如图所示,取BC的中点F,连接EF,OF,BC1.
因为E为CC1的中点,
所以EF∥BC1∥AD1,
故∠OEF或其补角即为异面直线OE与AD1所成的角,
设正方体ABCD-A1B1C1D1的棱长为2,
则在△OEF中,EF=,OE=,OF=1,
故∠OFE=90°,故cos∠OEF===.]
14.60°
解析 如图,在正四棱锥P-ABCD中,连接BD,交AC于点O,连接PO,
则PO⊥平面ABCD,在正四棱锥中,BO⊥平面PAC.
连接OE,DE,则∠BEO是直线BE和平面PAC所成的角.
∵正四棱锥P-ABCD的体积为2,底面积为6,
∴V=×6×PO=2,则PO=1,
BC=,则OC=OB=,
∵E为侧棱PC的中点,
∴取OC的中点H,连接EH,
则EH⊥OC,
EH=PO=,OH=OC=,
则OE=
==1.
在Rt△BOE中,
tan∠BEO===,
则∠BEO=60°.
15.AB [如图,当几何体S-ABCD为阳马时,SD⊥平面ABCD,
对于A,SD⊥平面ABCD,所以AC⊥SD,又AC⊥BD,SD∩BD=D,
故AC⊥平面SBD,所以AC⊥SB,故A正确;
对于B,因为AB∥CD,且AB 平面SCD,CD 平面SCD,故AB∥平面SCD,故B正确;
对于C,由A知,AC⊥平面SBD,连接SO,则∠ASO是SA与平面SBD所成的角,
因为SA=,OA=,
所以∠ASO=30°,故C不正确;
对于D,因为AB∥CD,所以∠SCD是AB与SC所成的角,因为SD=CD=1,所以∠SCD=45°,故D不正确.]
16.解 (1)如图,延长PE交AC于点F,连接BF,
∵AP,AB,AC两两互相垂直,
∴PA⊥平面ABC.
∵DE⊥平面ABC,
∴DE∥PA,
∴==,
∴F与C重合.
∵C∈PE,C∈AC,PE 平面PBE,AC 平面ABC,
∴C是平面PBE与平面ABC的公共点.
又B是平面PBE与平面ABC的公共点,
∴BC是平面PBE与平面ABC的交线.
(2)如图,连接AE.
∵AP,AB,AC两两互相垂直,
∴AB⊥平面PAC,
∴∠BEA为BE和平面PADE所成的角.
∵VB-PADE=S梯形ADEP·AB
=××(1+2)×1×AB=,
∴AB=.
又∵AE==,
∴tan∠BEA===,
所以BE和平面PADE所成角的正切值为.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
