18.2.2 菱形同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2.2 菱形
一、单选题
1.如图,在菱形 中,对角线 、 交于点 .若 , ,则 的长为( )
A.1 B. C.2 D.
2.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上.若点的坐标是,则点的坐标为( )
A. B. C. D.
3.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0)、B(0,2)、C(3,0)、D(0,-2),四边形ABCD是( ).
A.矩形 B.菱形 C.正方形 D.梯形
4.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
二、填空题
5.已知菱形ABCD的对角线AC=12 cm,BD=16cm,则这个菱形的面积为 cm.
6.如图,菱形对角线相交于点O,,则菱形的边长为 .
7.菱形的两条对角线长为2和 ,则菱形的周长为 .
三、解答题
8.如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 .若 ,求证:四边形 是菱形.
9.如图,在菱形ABCD中,两条对角线相交于点O,F在CD上,,连接OF并延长到E,使,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若,,求OD的长.
四、综合题
10.如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求平行四边形ABCD的面积.
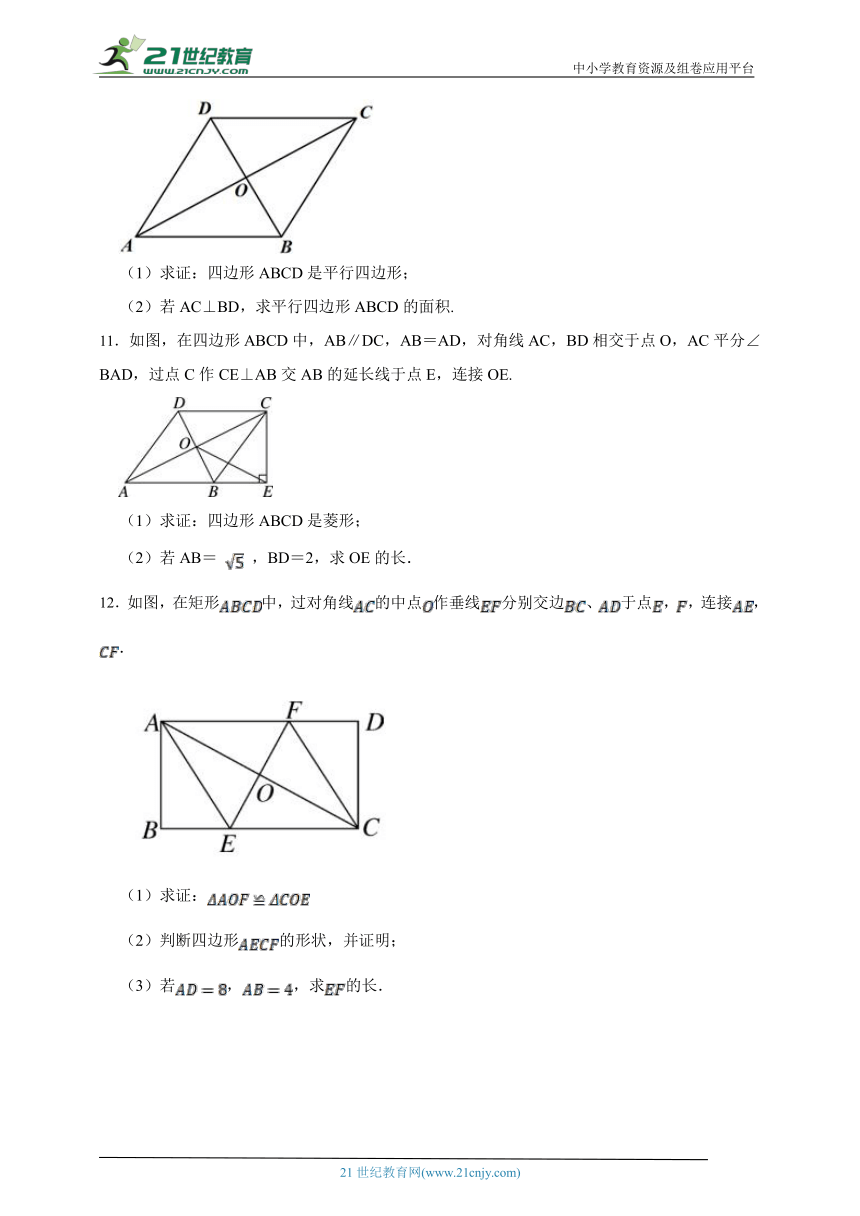
11.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD相交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB= ,BD=2,求OE的长.
12.如图,在矩形中,过对角线的中点作垂线分别交边、于点,,连接,.
(1)求证:
(2)判断四边形的形状,并证明;
(3)若,,求的长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD是菱形,
∴OC=OA=1,∠COD=90°, ∠CDO=12∠ADC=12×60 =30 .
∴CD=2OC=2×1=2,
故选C.
2.【答案】D
【解析】【解答】解:点的坐标为,
,
四边形是菱形,
,
点的横坐标为,纵坐标与点的纵坐标相同,即为4,
即,
故答案为:D.
【分析】利用勾股定理求出OA的长,再利用菱形的性质可得,再求出点B的坐标即可。
3.【答案】B
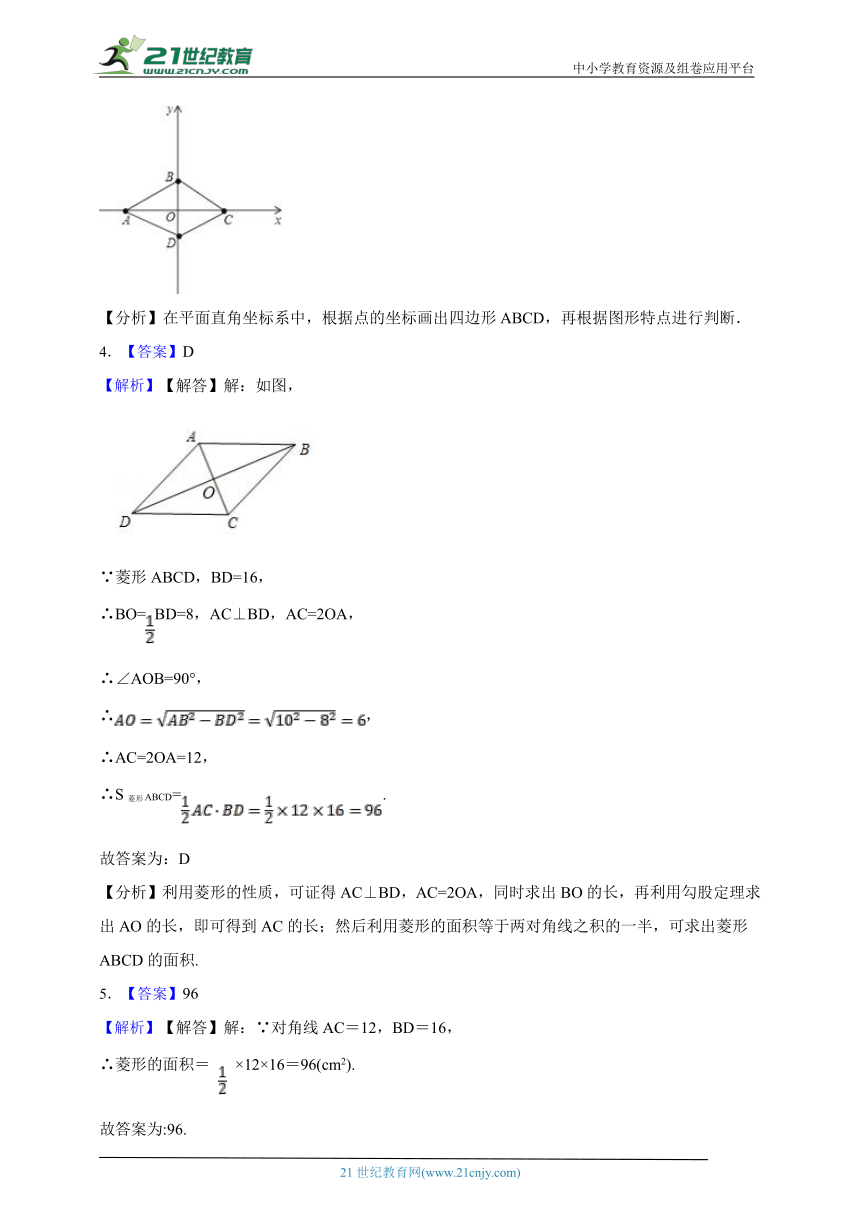
【解析】【解答】图形如图所示:∵A(-3,0)、B(0,2)、C(3,0)、D(0,-2),∴OA=OC,OB=OD,∴四边形ABCD为平行四边形,∵BD⊥AC,∴四边形ABCD为菱形,故选B.
【分析】在平面直角坐标系中,根据点的坐标画出四边形ABCD,再根据图形特点进行判断.
4.【答案】D
【解析】【解答】解:如图,
∵菱形ABCD,BD=16,
∴BO=BD=8,AC⊥BD,AC=2OA,
∴∠AOB=90°,
∴,
∴AC=2OA=12,
∴S菱形ABCD=.
故答案为:D
【分析】利用菱形的性质,可证得AC⊥BD,AC=2OA,同时求出BO的长,再利用勾股定理求出AO的长,即可得到AC的长;然后利用菱形的面积等于两对角线之积的一半,可求出菱形ABCD的面积.
5.【答案】96
【解析】【解答】解:∵对角线AC=12,BD=16,
∴菱形的面积= ×12×16=96(cm2).
故答案为:96.
【分析】根据菱形的面积等于对角线乘积的一半解答.
6.【答案】5
【解析】【解答】∵菱形对角线相交于点O,
∴ AC⊥BD,AO=OC=4,DO=BD=3
∴ AD==5
∴ 菱形的边长是5
【分析】本题考查菱形的性质和勾股定理的计算。菱形对角线互相平分且垂直,熟悉这一点很重要。
7.【答案】12
【解析】【解答】解:如图,
∵菱形ABCD,
∴AC⊥BD,AO=AC=,DO=BD=1,
∴∠AOD=90°,
在Rt△AOD中,,
∴菱形的周长为3×4=12.
【分析】利用菱形的性质可证得∠AOD=90°,同时可求出AO,OD的长;再利用勾股定理求出AD的长,然后求出菱形的周长。
8.【答案】证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠DAE=∠BCF,
∵DE∥BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB,
在△ADE和△CBF中,
∴△ADE≌△CBF(AAS),
∴DE=BF,
又∵DE∥BF,
∴四边形EBFD是平行四边形,
∵BE=DE,
∴四边形EBFD为菱形.
【解析】【分析】利用平行四边形的性质可得到AD=CB,AD∥CB, 再利用平行线的性质可推出∠DAE=∠BCF,∠AED=∠CFB,利用AAS证明△ADE≌△CBF,利用全等三角形的性质可推出DE=DF;然后根据有一组对边平行且相等的四边形是平行四边形,可知四边形EBFD是平行四边形,由一组邻边相等的平行四边形是菱形,可证得结论.
9.【答案】(1)证明:∵四边形ABCD是菱形,
∴,
∴,
∵,,
∴四边形OCED是平行四边形,
∵,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴,,,,
∵,
∴是等边三角形,
∴,,
∴,
∴.
【解析】【分析】(1)已知四边形ABCD是菱形,利用菱形的性质可得,,然后利用平行四边形的判定以及矩形的判定即可证明四边形OCED是矩形;
(2)已知,AD=2,是四边形ABCD是菱形,利用菱形的性质可得,,,然后可以证明三角形ABD是等边三角形,然后即可求出AD=2OD,然后求出OD即可.
10.【答案】(1)证明:如图,
∵AB//DC,
∴∠1=∠2 , ∠3=∠4
又∵AO=CO,
∴△AOB≌△COD,
∴OD=OB,
∴四边形ABCD是平行四边形
(2)解:∵AC⊥BD,
∴平行四边形ABCD是菱形,
∴平行四边形ABCD的面积为S= AC×BD=40.
【解析】【分析】(1)先证明△AOB≌△COD,可得OD=OB,从而根据对角线互相平分的四边形是平行四边形可证结论;
(2)先根据对角线互相垂直的平行四边形是菱形证明四边形ABCD是菱形,然后根据菱形的面积等于对角线乘积的一半计算即可.
11.【答案】(1)证明:∵AB∥DC,
∴∠DCA=∠CAB,
∵AC平分∠BAD,
∴∠CAB=∠DAC
∴∠DCA=∠DAC,
∴AD=DC
同理得:AD=AB,
∴AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形。
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,且AC与BD互相平分,
∵BD=2BO=2,∴BO=1
∵AO=
∴AO=2,
∴AC=2AO=4
∵CE⊥AB,
∴∠CEA=90°,AO=CO,
∴OE==2
【解析】【分析】(1)由AB与DC平行,可知∠DCA与∠CAB这一组内错角相等,再由已知条件中AC平分∠BAD,可知∠DAC与∠CAB相等,即可得到∠DAC与∠DCA相等,由等角对等边可知AD与DC相等,同理可知AD与AB相等,所以AB与DC这一组对边相等,再由AB与DC平行,可以判定四边形ABCD是平行四边形,再由已知中的AB与AD这一组邻边相等,即可证得四边形ABCD是菱形;
(2)由四边形ABCD是菱形,菱形的对角线互相垂直且平分,根据勾股定理可以求得AO的长,即可得到AC的长,再由CE与AE垂直,可知三角形ACE是直角三角形,点O是斜边AC上的中点,由直角三角形斜边上的中线等于斜边的一半,即可求得OE的长。
12.【答案】(1)证明:∵ 四边形ABCD是矩形
∴AD∥BC
∴∠FAC=∠ECA
∵O是AC的中点
∴OA=OC
又∠AOF=∠COE
∴ △AOF≌△COE.
(2)四边形AECF是菱形,
证明:由(1)得△AOF≌△COE
∴AF=CE
又AF∥EC
∴四边形AECF是平行四边形
又∵EF⊥AC
∴四边形AECF是菱形.
(3)解:∵四边形ABCD是矩形
∴CD=AB=4,∠D=90°
在Rt△ACD中,根据勾股定理得AC=..
又∵O是AC的中点
∴OC=
在Rt△CDF中,设CF=x,
∵四边形AECF是菱形.
∴AF=CF=x
则DF=8-x,根据勾股定理得:
解得x=5;即CF=5
在Rt△COF中,根据勾股定理得
所以EF=2OF=.
【解析】【分析】(1)根据矩形的性质可得AD∥BC,由平行线的性质可得∠FAC=∠ECA,根据中点的概念可得OA=OC,由对顶角的性质可得∠AOF=∠COE,然后根据全等三角形的判定定理进行证明;
(2)根据全等三角形的性质可得AF=CE,结合AF∥EC可得四边形AECF是平行四边形,然后根据EF⊥AC以及菱形的判定定理进行证明;
(3)根据矩形的性质可得CD=AB=4,∠D=90°,利用勾股定理可得AC,根据中点的概念可得OC,设CF=x,根据菱形的性质可得AF=CF=x,则DF=8-x,根据勾股定理得x,然后利用勾股定理求出OF,据此可得EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
18.2.2 菱形
一、单选题
1.如图,在菱形 中,对角线 、 交于点 .若 , ,则 的长为( )
A.1 B. C.2 D.
2.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上.若点的坐标是,则点的坐标为( )
A. B. C. D.
3.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0)、B(0,2)、C(3,0)、D(0,-2),四边形ABCD是( ).
A.矩形 B.菱形 C.正方形 D.梯形
4.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
二、填空题
5.已知菱形ABCD的对角线AC=12 cm,BD=16cm,则这个菱形的面积为 cm.
6.如图,菱形对角线相交于点O,,则菱形的边长为 .
7.菱形的两条对角线长为2和 ,则菱形的周长为 .
三、解答题
8.如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 .若 ,求证:四边形 是菱形.
9.如图,在菱形ABCD中,两条对角线相交于点O,F在CD上,,连接OF并延长到E,使,连接CE,DE.
(1)求证:四边形OCED是矩形;
(2)若,,求OD的长.
四、综合题
10.如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求平行四边形ABCD的面积.
11.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD相交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB= ,BD=2,求OE的长.
12.如图,在矩形中,过对角线的中点作垂线分别交边、于点,,连接,.
(1)求证:
(2)判断四边形的形状,并证明;
(3)若,,求的长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD是菱形,
∴OC=OA=1,∠COD=90°, ∠CDO=12∠ADC=12×60 =30 .
∴CD=2OC=2×1=2,
故选C.
2.【答案】D
【解析】【解答】解:点的坐标为,
,
四边形是菱形,
,
点的横坐标为,纵坐标与点的纵坐标相同,即为4,
即,
故答案为:D.
【分析】利用勾股定理求出OA的长,再利用菱形的性质可得,再求出点B的坐标即可。
3.【答案】B
【解析】【解答】图形如图所示:∵A(-3,0)、B(0,2)、C(3,0)、D(0,-2),∴OA=OC,OB=OD,∴四边形ABCD为平行四边形,∵BD⊥AC,∴四边形ABCD为菱形,故选B.
【分析】在平面直角坐标系中,根据点的坐标画出四边形ABCD,再根据图形特点进行判断.
4.【答案】D
【解析】【解答】解:如图,
∵菱形ABCD,BD=16,
∴BO=BD=8,AC⊥BD,AC=2OA,
∴∠AOB=90°,
∴,
∴AC=2OA=12,
∴S菱形ABCD=.
故答案为:D
【分析】利用菱形的性质,可证得AC⊥BD,AC=2OA,同时求出BO的长,再利用勾股定理求出AO的长,即可得到AC的长;然后利用菱形的面积等于两对角线之积的一半,可求出菱形ABCD的面积.
5.【答案】96
【解析】【解答】解:∵对角线AC=12,BD=16,
∴菱形的面积= ×12×16=96(cm2).
故答案为:96.
【分析】根据菱形的面积等于对角线乘积的一半解答.
6.【答案】5
【解析】【解答】∵菱形对角线相交于点O,
∴ AC⊥BD,AO=OC=4,DO=BD=3
∴ AD==5
∴ 菱形的边长是5
【分析】本题考查菱形的性质和勾股定理的计算。菱形对角线互相平分且垂直,熟悉这一点很重要。
7.【答案】12
【解析】【解答】解:如图,
∵菱形ABCD,
∴AC⊥BD,AO=AC=,DO=BD=1,
∴∠AOD=90°,
在Rt△AOD中,,
∴菱形的周长为3×4=12.
【分析】利用菱形的性质可证得∠AOD=90°,同时可求出AO,OD的长;再利用勾股定理求出AD的长,然后求出菱形的周长。
8.【答案】证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠DAE=∠BCF,
∵DE∥BF,
∴∠DEF=∠BFE,
∴∠AED=∠CFB,
在△ADE和△CBF中,
∴△ADE≌△CBF(AAS),
∴DE=BF,
又∵DE∥BF,
∴四边形EBFD是平行四边形,
∵BE=DE,
∴四边形EBFD为菱形.
【解析】【分析】利用平行四边形的性质可得到AD=CB,AD∥CB, 再利用平行线的性质可推出∠DAE=∠BCF,∠AED=∠CFB,利用AAS证明△ADE≌△CBF,利用全等三角形的性质可推出DE=DF;然后根据有一组对边平行且相等的四边形是平行四边形,可知四边形EBFD是平行四边形,由一组邻边相等的平行四边形是菱形,可证得结论.
9.【答案】(1)证明:∵四边形ABCD是菱形,
∴,
∴,
∵,,
∴四边形OCED是平行四边形,
∵,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,
∴,,,,
∵,
∴是等边三角形,
∴,,
∴,
∴.
【解析】【分析】(1)已知四边形ABCD是菱形,利用菱形的性质可得,,然后利用平行四边形的判定以及矩形的判定即可证明四边形OCED是矩形;
(2)已知,AD=2,是四边形ABCD是菱形,利用菱形的性质可得,,,然后可以证明三角形ABD是等边三角形,然后即可求出AD=2OD,然后求出OD即可.
10.【答案】(1)证明:如图,
∵AB//DC,
∴∠1=∠2 , ∠3=∠4
又∵AO=CO,
∴△AOB≌△COD,
∴OD=OB,
∴四边形ABCD是平行四边形
(2)解:∵AC⊥BD,
∴平行四边形ABCD是菱形,
∴平行四边形ABCD的面积为S= AC×BD=40.
【解析】【分析】(1)先证明△AOB≌△COD,可得OD=OB,从而根据对角线互相平分的四边形是平行四边形可证结论;
(2)先根据对角线互相垂直的平行四边形是菱形证明四边形ABCD是菱形,然后根据菱形的面积等于对角线乘积的一半计算即可.
11.【答案】(1)证明:∵AB∥DC,
∴∠DCA=∠CAB,
∵AC平分∠BAD,
∴∠CAB=∠DAC
∴∠DCA=∠DAC,
∴AD=DC
同理得:AD=AB,
∴AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形。
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,且AC与BD互相平分,
∵BD=2BO=2,∴BO=1
∵AO=
∴AO=2,
∴AC=2AO=4
∵CE⊥AB,
∴∠CEA=90°,AO=CO,
∴OE==2
【解析】【分析】(1)由AB与DC平行,可知∠DCA与∠CAB这一组内错角相等,再由已知条件中AC平分∠BAD,可知∠DAC与∠CAB相等,即可得到∠DAC与∠DCA相等,由等角对等边可知AD与DC相等,同理可知AD与AB相等,所以AB与DC这一组对边相等,再由AB与DC平行,可以判定四边形ABCD是平行四边形,再由已知中的AB与AD这一组邻边相等,即可证得四边形ABCD是菱形;
(2)由四边形ABCD是菱形,菱形的对角线互相垂直且平分,根据勾股定理可以求得AO的长,即可得到AC的长,再由CE与AE垂直,可知三角形ACE是直角三角形,点O是斜边AC上的中点,由直角三角形斜边上的中线等于斜边的一半,即可求得OE的长。
12.【答案】(1)证明:∵ 四边形ABCD是矩形
∴AD∥BC
∴∠FAC=∠ECA
∵O是AC的中点
∴OA=OC
又∠AOF=∠COE
∴ △AOF≌△COE.
(2)四边形AECF是菱形,
证明:由(1)得△AOF≌△COE
∴AF=CE
又AF∥EC
∴四边形AECF是平行四边形
又∵EF⊥AC
∴四边形AECF是菱形.
(3)解:∵四边形ABCD是矩形
∴CD=AB=4,∠D=90°
在Rt△ACD中,根据勾股定理得AC=..
又∵O是AC的中点
∴OC=
在Rt△CDF中,设CF=x,
∵四边形AECF是菱形.
∴AF=CF=x
则DF=8-x,根据勾股定理得:
解得x=5;即CF=5
在Rt△COF中,根据勾股定理得
所以EF=2OF=.
【解析】【分析】(1)根据矩形的性质可得AD∥BC,由平行线的性质可得∠FAC=∠ECA,根据中点的概念可得OA=OC,由对顶角的性质可得∠AOF=∠COE,然后根据全等三角形的判定定理进行证明;
(2)根据全等三角形的性质可得AF=CE,结合AF∥EC可得四边形AECF是平行四边形,然后根据EF⊥AC以及菱形的判定定理进行证明;
(3)根据矩形的性质可得CD=AB=4,∠D=90°,利用勾股定理可得AC,根据中点的概念可得OC,设CF=x,根据菱形的性质可得AF=CF=x,则DF=8-x,根据勾股定理得x,然后利用勾股定理求出OF,据此可得EF.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
