18.2 特殊的平行四边形本节综合练习题(含解析)
文档属性
| 名称 | 18.2 特殊的平行四边形本节综合练习题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
18.2 特殊的平行四边形本节综合练习题
一、单选题
1.下列说法正确的是( )
A.矩形的对角线互相垂直平分
B.对角线相等的菱形是正方形
C.两邻边相等的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
2.下列给出的条件中,能识别一个四边形是菱形的是( )
A.有一组对边平行且相等,有一个角是直角
B.两组对边分别相等,且有一组邻角相等
C.有一组对边平行,另一组对边相等,且对角线互相垂直
D.有一组对边平行且相等,且有一条对角线平分一个内角
3.下列说法正确的有( )
一组对边相等的四边形是矩形; 两条对角线相等的四边形是矩形; 四条边都相等且对角线互相垂直的四边形是正方形; 四条边都相等的四边形是菱形.
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是( )
A.AD=AB B.AB⊥AD C.AB=AC D.CA⊥BD
5.如图,菱形ABCD中,AC=8.BD=6.则菱形的面积为( )
A.20 B.40 C.28 D.24
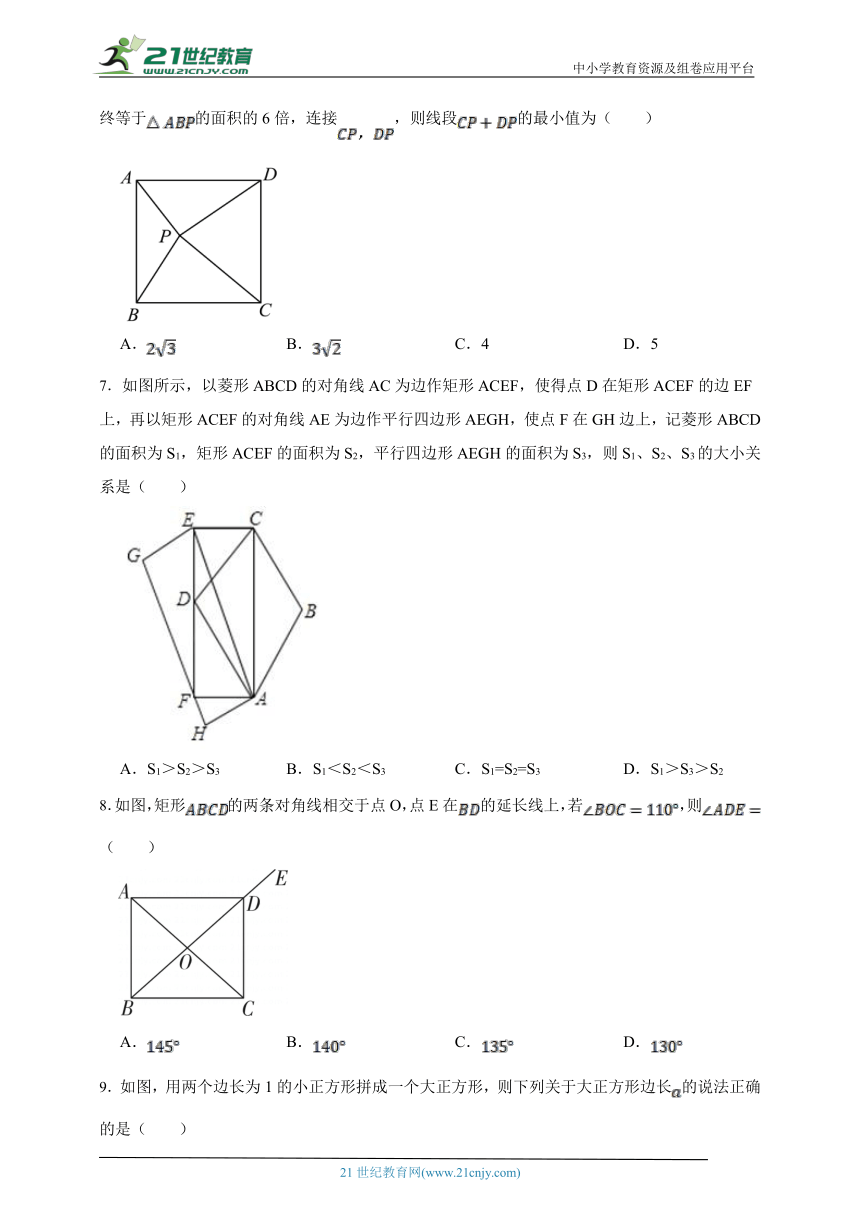
6.如图,正方形的边长为3,点P是正方形的内部一动点,且正方形的面积始终等于的面积的6倍,连接,则线段的最小值为( )
A. B. C.4 D.5
7.如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
A.S1>S2>S3 B.S1<S2<S3 C.S1=S2=S3 D.S1>S3>S2
8.如图,矩形的两条对角线相交于点O,点E在的延长线上,若,则( )
A. B. C. D.
9.如图,用两个边长为1的小正方形拼成一个大正方形,则下列关于大正方形边长的说法正确的是( )
A.是整数 B.满足 C.是分数 D.是无理数
10.下列命题中,假命题是( )
A.四个角都相等的四边形是矩形
B.两组对边分别相等的四边形是平行四边形
C.四条边都相等的四边形是正方形
D.两条对角线互相垂直平分的四边形是菱形
二、填空题
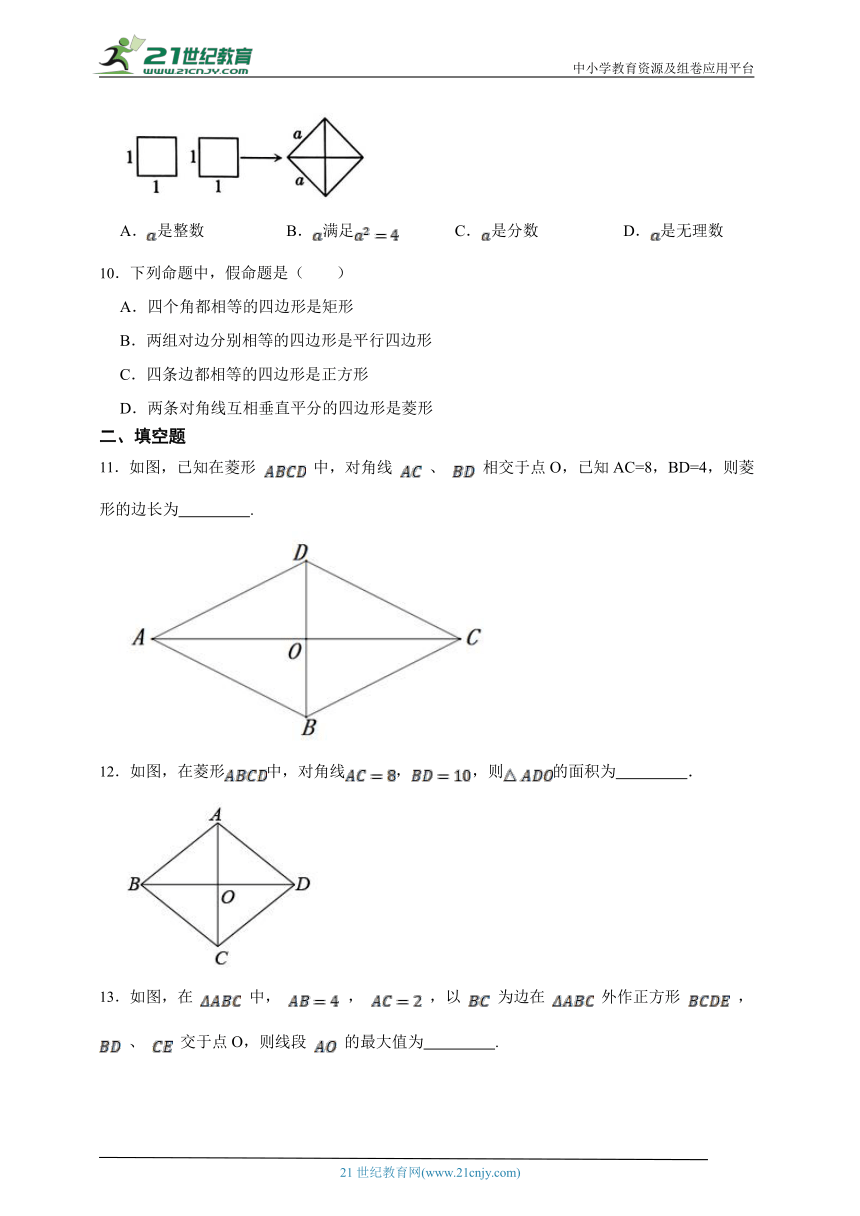
11.如图,已知在菱形 中,对角线 、 相交于点O,已知AC=8,BD=4,则菱形的边长为 .
12.如图,在菱形中,对角线,,则的面积为 .
13.如图,在 中, , ,以 为边在 外作正方形 , 、 交于点O,则线段 的最大值为 .
14.如图,长方形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,点E表示的实数是 .
15.已知直线的解析式为,菱形,,,…按图所示的方式放置,顶点,,,,…均在直线上,顶点,,,…均在轴上,则点的坐标是 .
三、作图题
16.如图,16个形状大小完全相同的菱形组成网格,菱形的顶点称为格点.
(1)在图1中画出矩形,使得,,,分别落在,,,边包含端点的格点上画出其中一个即可.
(2)如图2,已知点,,,,均在格点上,请在网格中包含边界找一格点,连结,使得直线平分平行四边形的面积.
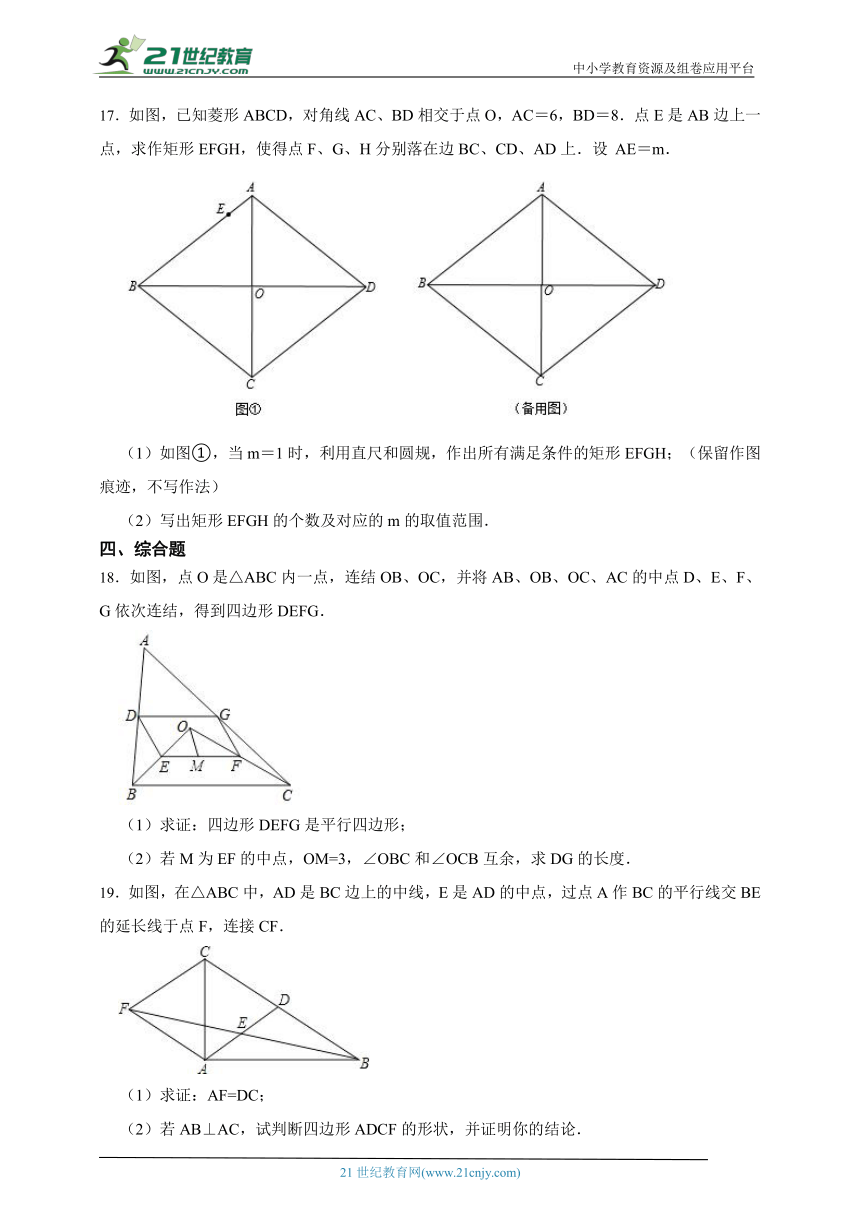
17.如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
四、综合题
18.如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
19.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
20.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
21.探索发现如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且,PE交CD于F.
(1)求证:;
(2) °.
(3)拓展延伸
如图,在菱形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且,,连接CE,请判断线段AP与线段CE的数量关系,并说明理由.
22.已知,在平行四边形 中, 为 上一点,且 ,连接 交 于点 ,过点 作 于 ,交 于点 .
(1)若 ,求 的度数;
(2)若 ,过点 作 交 于点 ,求证: .
答案解析部分
1.【答案】B
【解析】【解答】解: .矩形的对角线相等平分,不一定互相垂直,故 说法错误;
.对角线相等的菱形是正方形,正确;
.两邻边相等的平行四边形是菱形,故 说法错误;
.对角线互相垂直、相等且平分的四边形是正方形,故 说法错误.
故答案为: .
【分析】根据矩形,菱形,正方形的性质与判定分别判别即可.
2.【答案】D
【解析】【解答】A.错误,可判定为矩形,而不一定是菱形;B.错误,可判定为矩形,而不一定是菱形;C.错误,可判定为等腰梯形,而不是菱形;D.正确,有一组对边平行且相等可判定为平行四边形,有一条对角线平分一个内角,则可判定有一组邻边相等,而一组邻边相等的平行四边形是菱形.故答案为:D.
【分析】根据菱形的判定定理可知D正确。
3.【答案】A
【解析】【解答】解:(1)两组对边相等的四边形是平行四边形,故(1)错误;(2)两条对角线平分且相等的四边形是矩形,故(2)错误;(3)四条边都相等且对角线相等的四边形是正方形,故(3)错误;(4)四条边都相等的四边形是菱形,故(4)正确,
所以正确的有1个,
故答案为:A.
【分析】两组对边分别相等的四边形是平行四边形,一组对边相等的四边形可能是等腰梯形,也可能就是一个任意四边形,故(1)错误;两条对角线平分且相等的四边形是矩形或两条对角线相等的平行四边形是矩形,故(2)错误;(3)四条边都相等且对角线相等的四边形是正方形,或四条边相等且对角线相等的四边形是正方形,故(3)错误;(4)四条边都相等的四边形是菱形,故(4)正确,综上所述即可得出答案。
4.【答案】B
5.【答案】D
【解析】【解答】解: 菱形的面积为6×8÷2=24,
故答案为:D.
【分析】根据菱形的面积等于对角线乘积的一半可得答案.
6.【答案】D
【解析】【解答】解:作PQ⊥AB于点Q,
∵正方形的面积始终等于的面积的6倍,
∴S△ABP=×3×3=×3 PQ,
∴PQ=1,即P到AB的距离始终为1,
作直线PM ⊥AD于点M,交BC于点N,则点P在线段MN上运动,且四边形AQPM,BQPN均为矩形,
∴BN=PQ=1,
∴CN=2,
作点C关于MN对称点F,则点F在CB的延长线上,且CF=2CN=4,连接DF交MN于点P,则此时PD+PC最小,最小值为DF的长,
在Rt△DCF中,;
即线段CP+DP的最小值是5;
故答案为:D.
【分析】根据题意得出P到AB的距离始终为1,作点C关于MN对称点F,则点F在CB的延长线上,且CF=2CN=4,连接DF交MN于点P,则此时PD+PC最小,最小值为DF的长,勾股定理即可求解.
7.【答案】C
【解析】【解答】解:连接BD交AC于N,作FM⊥AB于M,如图所示:
∵四边形ABCD是菱形,
∴BD⊥AC,DN=BD,菱形ABCD的面积S1=AC BD=AC DN,
∵四边形ACEF是矩形,
∴AC=EF,CE=AF,∠AFD=∠DEC=∠ECN=90°,矩形ACEF的面积为S2=AC CE,
∴四边形CEDN是矩形,
∴DN=CE,
∴S1=S2,
∵△直角三角形AEF的面积=AE FM=EF AF=AC CE,
∴EF AF=AC CE,
∵平行四边形AEGH的面积为S3=AE FM,
∴S1=S2=S3;
故选:C.
【分析】连接BD交AC于N,作FM⊥AB于M,由菱形的性质得出BD⊥AC,DN=BD,S1=AC BD=AC DN,由矩形的性质得出AC=EF,CE=AF,∠AFD=∠DEC=∠ECN=90°,S2=AC CE,得出DN=CE,S1=S2,由直角三角形AEF的面积得出EF AF=AC CE,S3=AE FM,S1=S2=S3;即可得出结论.
8.【答案】A
【解析】【解答】
解:∵四边形ABCD是矩形
∴AO=DO
∴∠OAD=∠ODA
又∵∠BOC=110°
∴∠AOD=∠BOC=110°
∴在△AOD中,
∠OAD=∠ODA=(180°-∠AOD)=(180°-110°)=35°
∴∠ADE=180°-∠ODA=180°-35°=145°
故正确答案是:A
【分析】本题运用矩形的性质得出对角线相等且互相平分,然后运用三角形的内角和从而求出角的度数。
9.【答案】D
【解析】【解答】∵两个正方形的边长均是1,
∴两个小正方形的面积都是1,
∴拼接成的大正方形的面积为2,
∴此时大正方形的边长为a=,
∴a为无理数,
故答案为:D.
【分析】先求出拼接成的大正方形的面积为2,再利用正方形的面积公式求出边长为,再逐项分析判断即可.
10.【答案】C
【解析】【解答】解:A、四个角都相等的四边形是矩形,真命题;
B、两组对边分别相等的四边形是平行四边形 ,真命题;
C、四条边都相等的四边形是菱形,假命题;
D、两条对角线互相垂直平分的四边形是菱形 ,真命题;
故答案为:C.
【分析】根据矩形的判定、平行四边形的判定、正方形的判定、菱形的判定逐一判断即可.
11.【答案】
【解析】【解答】解:∵四边形ABCD是菱形,且AC=8,BD=4,
∴OA= AC=4,OB= BD=2,AC⊥BD,
∴ .
故答案为: .
【分析】由菱形的性质可得菱形的对角线互相垂直平分,再用勾股定理可求解.
12.【答案】10
【解析】【解答】解:在菱形ABCD中,对角线,,
∴OA=4,OD=5,AC⊥BD,
∴的面积为.
故答案为:10.
【分析】根据菱形的性质可得OA=AC=4,OD=BD=5,AC⊥BD,然后根据三角形的面积公式进行计算.
13.【答案】
【解析】【解答】如图,过O作OF⊥AO且使OF=AO,连接AF、CF,
∴∠AOF=90°,△AOF是等腰直角三角形,
∴AF= AO,
∵四边形BCDE是正方形,
∴OB=OC,∠BOC=90°,
∵∠BOC=∠AOF=90°,
∴∠AOB+∠AOC=∠COF+∠AOC,
∴∠AOB=∠COF,
又∵OB=OC,AO=OF,
∴△AOB≌△COF,
∴CF=AB=4,
当点A、C、F三点不共线时,AC+CF>AF,
当点A、C、F三点共线时,AC+CF=AC+AB=AF=6,
∴AF≤AC+CF=6,
∴AF的最大值是6,
∴AF= AO=6,
∴AO= .
故答案为:
【分析】过O作OF⊥AO且使OF=AO,连接AF、CF,可知△AOF是等腰直角三角形,进而可得AF= AO,根据正方形的性质可得OB=OC,∠BOC=90°,进而可得∠AOB=∠COF,进而可得△AOB≌△COF,即可证明AB=CF,当点A、C、F三点不共线时,根据三角形的三边关系可得AC+CF>AF,当点A、C、F三点共线时可得AC+CF=AC+AB=AF=6,即可得AF的最大值,由AF= AO即可得答案.
14.【答案】 1
【解析】【解答】解:∵四边形ABCD是长方形,
∴AD=BC=2,CD=AB=1,∠ADC=90°,
在Rt△ACD中,由勾股定理可得:
AC= =
∵点A在数轴上对应的数是-1,
∴点E表示的实数是 .
故答案为: .
【分析】由长方形的性质可得AD=BC=2,CD=AB=1,∠ADC=90°,由勾股定理求出AC,然后结合点A在数轴上表示的数就可得到点E表示的实数.
15.【答案】
【解析】【解答】解:设直线l: 与x轴交于点C,如图所示:
令y=0,即2x+2=0,x=-1,则C(-1,0)
令x=0,得y=2,则
∵ 四边形 为菱形
∴ AO垂直平分
∴
∴ 当x=1时,y=4,∴
则,
以此类推,可以发现:,·······
∴则点的坐标是
故答案为: .
【分析】本题考查菱形的性质,一次函数点的特征,找出点坐标的规律是关键。
16.【答案】(1)解:如图所示:只需要画出其中一个即可.
(2)解:由题意,点 即为所求;
【解析】【分析】(1)根据矩形的对角线相等且互相平分,借助网格纸的特点,根据菱形的中点对称性,过菱形的对角线交点的任意两点直线与AD、CD、BC、AB分别相交于点E、F、M、N,再顺次连接这四点即可;
(2)利用网格纸的特点,四边形EFMN是平行四边形,根据平行四边形的中心对称性,过四边形EFMN对角线交点及点P的直线就能将四边形EFMN的面积平分,据此作图即可得到符合题意的点Q.
17.【答案】(1)解:如图①,如图②(也可以用图①的方法,取⊙O与边BC、CD、AD的另一个交点即可)
(2)解:∵O到菱形边的距离为 ,当⊙O与AB相切时AE= ,当过点A,C时,⊙O与AB交于A,E两点,此时AE= ×2= ,根据图像可得如下六种情形:
①当m=0时,如图,存在1个矩形EFGH;
②当0<m< 时,如图,存在2个矩形EFGH;
③当m= 时,如图,存在1个矩形EFGH;
④当 <m≤ 时,如图,存在2个矩形EFGH;
⑤当 <m<5时,如图,存在1个矩形EFGH;
⑥当m=5时,不存在矩形EFGH
【解析】【分析】(1)以O点为圆心,OE长为半径画圆,与菱形产生交点,顺次连接圆O与菱形每条边的同侧交点即可;(2)分别考虑以O为圆心,OE为半径的圆与每条边的线段有几个交点时的情形,共分五种情况.
18.【答案】(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG= BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF= BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形。
(2)解:∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6。
【解析】【分析】(1)根据三角形中位线的性质得出DG∥BC,DG= BC;EF∥BC,EF= BC;根据平行于同一直线的两条直线互相平行及等量代换得出DG=EF,DG∥EF,根据一组对边平行且相等的四边形是平行四边形得出结论;
(2)根据余角的定义得出∠OBC+∠OCB=90°,根据三角形的内角和得出∠BOC=90°,然后根据直角三角形斜边上的中线等于斜边的一半得出EF=2OM=6,根据平行四边形对边相等得出DG=EF=6。
19.【答案】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC
(2)解:四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD= BC=DC,
∴平行四边形ADCF是菱形
【解析】【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
20.【答案】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE∥AC,AC=2DE,
∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE
(2)解: 当∠B=30°时,四边形ACEF是菱形;理由如下:
∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC= AB=AE,∴△AEC是等边三角形,∴AC=CE,
又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形
【解析】【分析】(1)连接三角形两边中点的线段是三角形的中位线,三角形的中位线平行于第三边,并且等于第三边的一半,从而得出DE∥AC,AC=2DE,又EF=2DE,故EF∥AC,EF=AC,根据一组对边平行且相等的四边形是平行四边形得出四边形ACEF是平行四边形,根据平行四边形对边相等得出AF=CE;
(2) 当∠B=30°时,四边形ACEF是菱形;理由如下:根据三角形的内角和得出∠BAC=60°,根据含30°直角三角形的边之间的关系得出AC= AB=AE,根据有一个角是60°的等腰三角形是等边三角形得出△AEC是等边三角形,根据等边三角形的三边相等得出AC=CE,根据有一组邻边相等的平行四边形是菱形得出结论。
21.【答案】(1)证明:∵四边形ABCD是正方形,
∴,,
∵,
∴,
∴,
∵,
∴;
(2)90
(3)解:∵四边形ABCD是菱形,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴是等边三角形,
∴,
∵,
∴.
【解析】【解答】解:(2)∵,
∴,
∵,
∴,
∴,
∵,
∴,
故答案为:90;
【分析】(1)由正方形的性质可得AD=CD,∠ADP=∠CDP=45°, 根据SAS证明△ADP≌△CDP,可得PA=PC,由PA=PE可得PC=PE;
(2)由△ADP≌△CDP可得,由可得,从而得出∠DCP=∠DEP,由对顶角相等可得从而得出,继而得解.
22.【答案】(1)解:如图,
,
,
,
,
,
又∵平行四边形 中, ,
,
;
(2)证明:如图,过 作 于 ,过 作 于 ,
则 ,
由(1)可得, ,
,
在 和 中,
,
,
又 矩形 中, ,
, ,
,
即 ,
,
在 和 中,
,
, ,
,
,
.
【解析】【分析】(1)根据平行四边形的性质证明即可;(2)先证明 ,再利用矩形的性质可证 ,根据等角对等边可得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
18.2 特殊的平行四边形本节综合练习题
一、单选题
1.下列说法正确的是( )
A.矩形的对角线互相垂直平分
B.对角线相等的菱形是正方形
C.两邻边相等的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
2.下列给出的条件中,能识别一个四边形是菱形的是( )
A.有一组对边平行且相等,有一个角是直角
B.两组对边分别相等,且有一组邻角相等
C.有一组对边平行,另一组对边相等,且对角线互相垂直
D.有一组对边平行且相等,且有一条对角线平分一个内角
3.下列说法正确的有( )
一组对边相等的四边形是矩形; 两条对角线相等的四边形是矩形; 四条边都相等且对角线互相垂直的四边形是正方形; 四条边都相等的四边形是菱形.
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是( )
A.AD=AB B.AB⊥AD C.AB=AC D.CA⊥BD
5.如图,菱形ABCD中,AC=8.BD=6.则菱形的面积为( )
A.20 B.40 C.28 D.24
6.如图,正方形的边长为3,点P是正方形的内部一动点,且正方形的面积始终等于的面积的6倍,连接,则线段的最小值为( )
A. B. C.4 D.5
7.如图所示,以菱形ABCD的对角线AC为边作矩形ACEF,使得点D在矩形ACEF的边EF上,再以矩形ACEF的对角线AE为边作平行四边形AEGH,使点F在GH边上,记菱形ABCD的面积为S1,矩形ACEF的面积为S2,平行四边形AEGH的面积为S3,则S1、S2、S3的大小关系是( )
A.S1>S2>S3 B.S1<S2<S3 C.S1=S2=S3 D.S1>S3>S2
8.如图,矩形的两条对角线相交于点O,点E在的延长线上,若,则( )
A. B. C. D.
9.如图,用两个边长为1的小正方形拼成一个大正方形,则下列关于大正方形边长的说法正确的是( )
A.是整数 B.满足 C.是分数 D.是无理数
10.下列命题中,假命题是( )
A.四个角都相等的四边形是矩形
B.两组对边分别相等的四边形是平行四边形
C.四条边都相等的四边形是正方形
D.两条对角线互相垂直平分的四边形是菱形
二、填空题
11.如图,已知在菱形 中,对角线 、 相交于点O,已知AC=8,BD=4,则菱形的边长为 .
12.如图,在菱形中,对角线,,则的面积为 .
13.如图,在 中, , ,以 为边在 外作正方形 , 、 交于点O,则线段 的最大值为 .
14.如图,长方形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,点E表示的实数是 .
15.已知直线的解析式为,菱形,,,…按图所示的方式放置,顶点,,,,…均在直线上,顶点,,,…均在轴上,则点的坐标是 .
三、作图题
16.如图,16个形状大小完全相同的菱形组成网格,菱形的顶点称为格点.
(1)在图1中画出矩形,使得,,,分别落在,,,边包含端点的格点上画出其中一个即可.
(2)如图2,已知点,,,,均在格点上,请在网格中包含边界找一格点,连结,使得直线平分平行四边形的面积.
17.如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.
(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
四、综合题
18.如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
19.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
20.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
21.探索发现如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且,PE交CD于F.
(1)求证:;
(2) °.
(3)拓展延伸
如图,在菱形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且,,连接CE,请判断线段AP与线段CE的数量关系,并说明理由.
22.已知,在平行四边形 中, 为 上一点,且 ,连接 交 于点 ,过点 作 于 ,交 于点 .
(1)若 ,求 的度数;
(2)若 ,过点 作 交 于点 ,求证: .
答案解析部分
1.【答案】B
【解析】【解答】解: .矩形的对角线相等平分,不一定互相垂直,故 说法错误;
.对角线相等的菱形是正方形,正确;
.两邻边相等的平行四边形是菱形,故 说法错误;
.对角线互相垂直、相等且平分的四边形是正方形,故 说法错误.
故答案为: .
【分析】根据矩形,菱形,正方形的性质与判定分别判别即可.
2.【答案】D
【解析】【解答】A.错误,可判定为矩形,而不一定是菱形;B.错误,可判定为矩形,而不一定是菱形;C.错误,可判定为等腰梯形,而不是菱形;D.正确,有一组对边平行且相等可判定为平行四边形,有一条对角线平分一个内角,则可判定有一组邻边相等,而一组邻边相等的平行四边形是菱形.故答案为:D.
【分析】根据菱形的判定定理可知D正确。
3.【答案】A
【解析】【解答】解:(1)两组对边相等的四边形是平行四边形,故(1)错误;(2)两条对角线平分且相等的四边形是矩形,故(2)错误;(3)四条边都相等且对角线相等的四边形是正方形,故(3)错误;(4)四条边都相等的四边形是菱形,故(4)正确,
所以正确的有1个,
故答案为:A.
【分析】两组对边分别相等的四边形是平行四边形,一组对边相等的四边形可能是等腰梯形,也可能就是一个任意四边形,故(1)错误;两条对角线平分且相等的四边形是矩形或两条对角线相等的平行四边形是矩形,故(2)错误;(3)四条边都相等且对角线相等的四边形是正方形,或四条边相等且对角线相等的四边形是正方形,故(3)错误;(4)四条边都相等的四边形是菱形,故(4)正确,综上所述即可得出答案。
4.【答案】B
5.【答案】D
【解析】【解答】解: 菱形的面积为6×8÷2=24,
故答案为:D.
【分析】根据菱形的面积等于对角线乘积的一半可得答案.
6.【答案】D
【解析】【解答】解:作PQ⊥AB于点Q,
∵正方形的面积始终等于的面积的6倍,
∴S△ABP=×3×3=×3 PQ,
∴PQ=1,即P到AB的距离始终为1,
作直线PM ⊥AD于点M,交BC于点N,则点P在线段MN上运动,且四边形AQPM,BQPN均为矩形,
∴BN=PQ=1,
∴CN=2,
作点C关于MN对称点F,则点F在CB的延长线上,且CF=2CN=4,连接DF交MN于点P,则此时PD+PC最小,最小值为DF的长,
在Rt△DCF中,;
即线段CP+DP的最小值是5;
故答案为:D.
【分析】根据题意得出P到AB的距离始终为1,作点C关于MN对称点F,则点F在CB的延长线上,且CF=2CN=4,连接DF交MN于点P,则此时PD+PC最小,最小值为DF的长,勾股定理即可求解.
7.【答案】C
【解析】【解答】解:连接BD交AC于N,作FM⊥AB于M,如图所示:
∵四边形ABCD是菱形,
∴BD⊥AC,DN=BD,菱形ABCD的面积S1=AC BD=AC DN,
∵四边形ACEF是矩形,
∴AC=EF,CE=AF,∠AFD=∠DEC=∠ECN=90°,矩形ACEF的面积为S2=AC CE,
∴四边形CEDN是矩形,
∴DN=CE,
∴S1=S2,
∵△直角三角形AEF的面积=AE FM=EF AF=AC CE,
∴EF AF=AC CE,
∵平行四边形AEGH的面积为S3=AE FM,
∴S1=S2=S3;
故选:C.
【分析】连接BD交AC于N,作FM⊥AB于M,由菱形的性质得出BD⊥AC,DN=BD,S1=AC BD=AC DN,由矩形的性质得出AC=EF,CE=AF,∠AFD=∠DEC=∠ECN=90°,S2=AC CE,得出DN=CE,S1=S2,由直角三角形AEF的面积得出EF AF=AC CE,S3=AE FM,S1=S2=S3;即可得出结论.
8.【答案】A
【解析】【解答】
解:∵四边形ABCD是矩形
∴AO=DO
∴∠OAD=∠ODA
又∵∠BOC=110°
∴∠AOD=∠BOC=110°
∴在△AOD中,
∠OAD=∠ODA=(180°-∠AOD)=(180°-110°)=35°
∴∠ADE=180°-∠ODA=180°-35°=145°
故正确答案是:A
【分析】本题运用矩形的性质得出对角线相等且互相平分,然后运用三角形的内角和从而求出角的度数。
9.【答案】D
【解析】【解答】∵两个正方形的边长均是1,
∴两个小正方形的面积都是1,
∴拼接成的大正方形的面积为2,
∴此时大正方形的边长为a=,
∴a为无理数,
故答案为:D.
【分析】先求出拼接成的大正方形的面积为2,再利用正方形的面积公式求出边长为,再逐项分析判断即可.
10.【答案】C
【解析】【解答】解:A、四个角都相等的四边形是矩形,真命题;
B、两组对边分别相等的四边形是平行四边形 ,真命题;
C、四条边都相等的四边形是菱形,假命题;
D、两条对角线互相垂直平分的四边形是菱形 ,真命题;
故答案为:C.
【分析】根据矩形的判定、平行四边形的判定、正方形的判定、菱形的判定逐一判断即可.
11.【答案】
【解析】【解答】解:∵四边形ABCD是菱形,且AC=8,BD=4,
∴OA= AC=4,OB= BD=2,AC⊥BD,
∴ .
故答案为: .
【分析】由菱形的性质可得菱形的对角线互相垂直平分,再用勾股定理可求解.
12.【答案】10
【解析】【解答】解:在菱形ABCD中,对角线,,
∴OA=4,OD=5,AC⊥BD,
∴的面积为.
故答案为:10.
【分析】根据菱形的性质可得OA=AC=4,OD=BD=5,AC⊥BD,然后根据三角形的面积公式进行计算.
13.【答案】
【解析】【解答】如图,过O作OF⊥AO且使OF=AO,连接AF、CF,
∴∠AOF=90°,△AOF是等腰直角三角形,
∴AF= AO,
∵四边形BCDE是正方形,
∴OB=OC,∠BOC=90°,
∵∠BOC=∠AOF=90°,
∴∠AOB+∠AOC=∠COF+∠AOC,
∴∠AOB=∠COF,
又∵OB=OC,AO=OF,
∴△AOB≌△COF,
∴CF=AB=4,
当点A、C、F三点不共线时,AC+CF>AF,
当点A、C、F三点共线时,AC+CF=AC+AB=AF=6,
∴AF≤AC+CF=6,
∴AF的最大值是6,
∴AF= AO=6,
∴AO= .
故答案为:
【分析】过O作OF⊥AO且使OF=AO,连接AF、CF,可知△AOF是等腰直角三角形,进而可得AF= AO,根据正方形的性质可得OB=OC,∠BOC=90°,进而可得∠AOB=∠COF,进而可得△AOB≌△COF,即可证明AB=CF,当点A、C、F三点不共线时,根据三角形的三边关系可得AC+CF>AF,当点A、C、F三点共线时可得AC+CF=AC+AB=AF=6,即可得AF的最大值,由AF= AO即可得答案.
14.【答案】 1
【解析】【解答】解:∵四边形ABCD是长方形,
∴AD=BC=2,CD=AB=1,∠ADC=90°,
在Rt△ACD中,由勾股定理可得:
AC= =
∵点A在数轴上对应的数是-1,
∴点E表示的实数是 .
故答案为: .
【分析】由长方形的性质可得AD=BC=2,CD=AB=1,∠ADC=90°,由勾股定理求出AC,然后结合点A在数轴上表示的数就可得到点E表示的实数.
15.【答案】
【解析】【解答】解:设直线l: 与x轴交于点C,如图所示:
令y=0,即2x+2=0,x=-1,则C(-1,0)
令x=0,得y=2,则
∵ 四边形 为菱形
∴ AO垂直平分
∴
∴ 当x=1时,y=4,∴
则,
以此类推,可以发现:,·······
∴则点的坐标是
故答案为: .
【分析】本题考查菱形的性质,一次函数点的特征,找出点坐标的规律是关键。
16.【答案】(1)解:如图所示:只需要画出其中一个即可.
(2)解:由题意,点 即为所求;
【解析】【分析】(1)根据矩形的对角线相等且互相平分,借助网格纸的特点,根据菱形的中点对称性,过菱形的对角线交点的任意两点直线与AD、CD、BC、AB分别相交于点E、F、M、N,再顺次连接这四点即可;
(2)利用网格纸的特点,四边形EFMN是平行四边形,根据平行四边形的中心对称性,过四边形EFMN对角线交点及点P的直线就能将四边形EFMN的面积平分,据此作图即可得到符合题意的点Q.
17.【答案】(1)解:如图①,如图②(也可以用图①的方法,取⊙O与边BC、CD、AD的另一个交点即可)
(2)解:∵O到菱形边的距离为 ,当⊙O与AB相切时AE= ,当过点A,C时,⊙O与AB交于A,E两点,此时AE= ×2= ,根据图像可得如下六种情形:
①当m=0时,如图,存在1个矩形EFGH;
②当0<m< 时,如图,存在2个矩形EFGH;
③当m= 时,如图,存在1个矩形EFGH;
④当 <m≤ 时,如图,存在2个矩形EFGH;
⑤当 <m<5时,如图,存在1个矩形EFGH;
⑥当m=5时,不存在矩形EFGH
【解析】【分析】(1)以O点为圆心,OE长为半径画圆,与菱形产生交点,顺次连接圆O与菱形每条边的同侧交点即可;(2)分别考虑以O为圆心,OE为半径的圆与每条边的线段有几个交点时的情形,共分五种情况.
18.【答案】(1)证明:∵D、G分别是AB、AC的中点,
∴DG∥BC,DG= BC,
∵E、F分别是OB、OC的中点,
∴EF∥BC,EF= BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形。
(2)解:∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵M为EF的中点,OM=3,
∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,
∴DG=EF=6。
【解析】【分析】(1)根据三角形中位线的性质得出DG∥BC,DG= BC;EF∥BC,EF= BC;根据平行于同一直线的两条直线互相平行及等量代换得出DG=EF,DG∥EF,根据一组对边平行且相等的四边形是平行四边形得出结论;
(2)根据余角的定义得出∠OBC+∠OCB=90°,根据三角形的内角和得出∠BOC=90°,然后根据直角三角形斜边上的中线等于斜边的一半得出EF=2OM=6,根据平行四边形对边相等得出DG=EF=6。
19.【答案】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC
(2)解:四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD= BC=DC,
∴平行四边形ADCF是菱形
【解析】【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
20.【答案】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE∥AC,AC=2DE,
∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE
(2)解: 当∠B=30°时,四边形ACEF是菱形;理由如下:
∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC= AB=AE,∴△AEC是等边三角形,∴AC=CE,
又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形
【解析】【分析】(1)连接三角形两边中点的线段是三角形的中位线,三角形的中位线平行于第三边,并且等于第三边的一半,从而得出DE∥AC,AC=2DE,又EF=2DE,故EF∥AC,EF=AC,根据一组对边平行且相等的四边形是平行四边形得出四边形ACEF是平行四边形,根据平行四边形对边相等得出AF=CE;
(2) 当∠B=30°时,四边形ACEF是菱形;理由如下:根据三角形的内角和得出∠BAC=60°,根据含30°直角三角形的边之间的关系得出AC= AB=AE,根据有一个角是60°的等腰三角形是等边三角形得出△AEC是等边三角形,根据等边三角形的三边相等得出AC=CE,根据有一组邻边相等的平行四边形是菱形得出结论。
21.【答案】(1)证明:∵四边形ABCD是正方形,
∴,,
∵,
∴,
∴,
∵,
∴;
(2)90
(3)解:∵四边形ABCD是菱形,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴是等边三角形,
∴,
∵,
∴.
【解析】【解答】解:(2)∵,
∴,
∵,
∴,
∴,
∵,
∴,
故答案为:90;
【分析】(1)由正方形的性质可得AD=CD,∠ADP=∠CDP=45°, 根据SAS证明△ADP≌△CDP,可得PA=PC,由PA=PE可得PC=PE;
(2)由△ADP≌△CDP可得,由可得,从而得出∠DCP=∠DEP,由对顶角相等可得从而得出,继而得解.
22.【答案】(1)解:如图,
,
,
,
,
,
又∵平行四边形 中, ,
,
;
(2)证明:如图,过 作 于 ,过 作 于 ,
则 ,
由(1)可得, ,
,
在 和 中,
,
,
又 矩形 中, ,
, ,
,
即 ,
,
在 和 中,
,
, ,
,
,
.
【解析】【分析】(1)根据平行四边形的性质证明即可;(2)先证明 ,再利用矩形的性质可证 ,根据等角对等边可得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
