19.1.1 变量与函数同步练习(含解析)
文档属性
| 名称 | 19.1.1 变量与函数同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
19.1.1 变量与函数
一、填空题
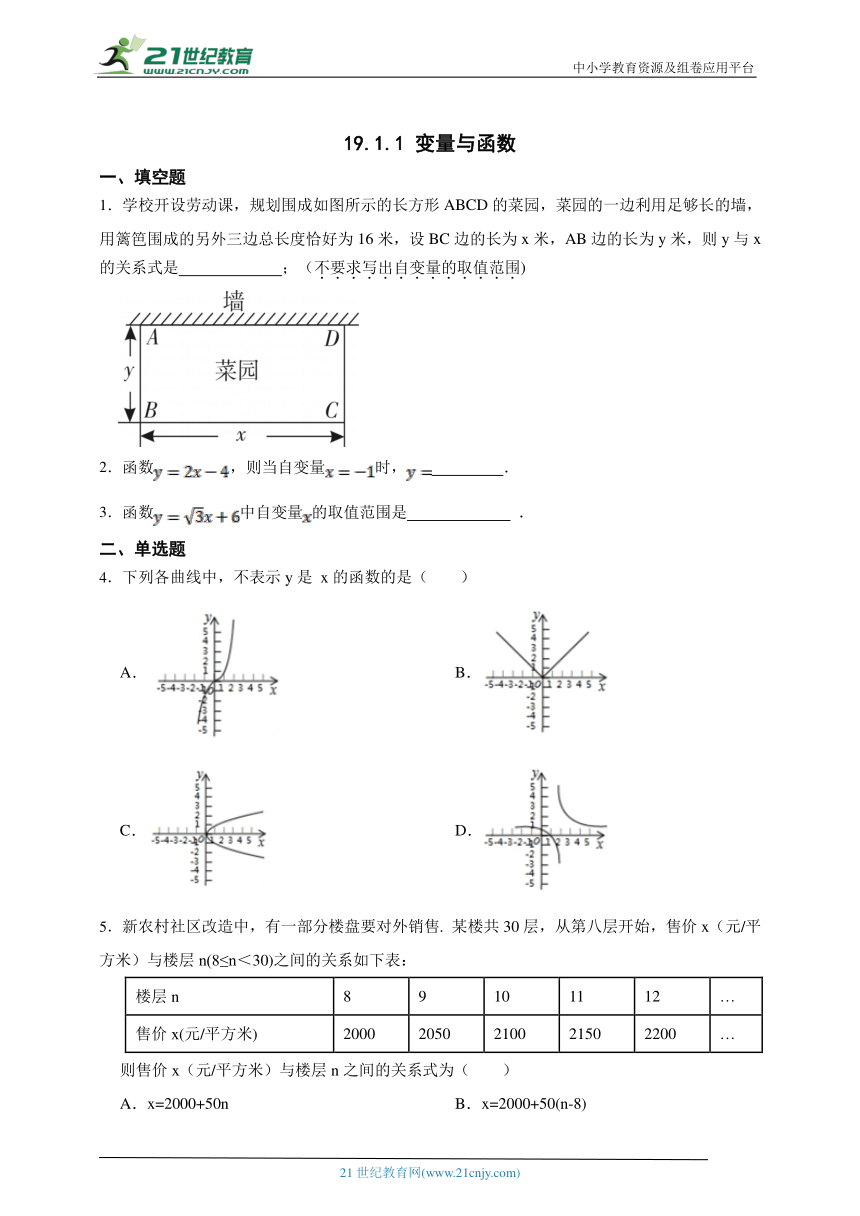
1.学校开设劳动课,规划围成如图所示的长方形ABCD的菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为16米,设BC边的长为x米,AB边的长为y米,则y与x的关系式是 ;(不要求写出自变量的取值范围)
2.函数,则当自变量时, .
3.函数中自变量的取值范围是 .
二、单选题
4.下列各曲线中,不表示y是 x的函数的是( )
A. B.
C. D.
5.新农村社区改造中,有一部分楼盘要对外销售. 某楼共30层,从第八层开始,售价x(元/平方米)与楼层n(8≤n<30)之间的关系如下表:
楼层n 8 9 10 11 12 …
售价x(元/平方米) 2000 2050 2100 2150 2200 …
则售价x(元/平方米)与楼层n之间的关系式为( )
A.x=2000+50n B.x=2000+50(n-8)
C.n=2000+50(x-8) D.n=2000+50x
6.下列关系中,不是函数的是( ).
A.y= B.y=-x2+2x
C.y=9 (x≥0) D.y=±x2
7.利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题的因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水管
三、解答题
8.如图,正方形ABCD的边长为10cm,动点M,N同时从点A出发,点M沿AB边向终点B移动,点N沿AD边向终点D移动,速度都是1cm/s,移动的时间是x(s).求△AMN的面积y(cm2)关于x(s)的函数表达式及自变量x的取值范围.
9.已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
四、综合题
10.华氏温度f(℉)与摄氏温度c(℃)之间存在如下的关系f= c+32.
(1)一个人的体温有可能达到100℉吗(精确到0.1)?
(2)如果某地早晨的摄氏温度为15℃,那么此地早晨的华氏温度是多少?
(3)若当地某一时刻的华氏温度为68℉,则该时刻摄氏温度是多少?
11.下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 1 2 3 4 5 6 7 8 9
卖钱额/元 2 4 6 8 10 12 14 16 18
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;
(3)当橘子卖出50千克时,预测卖钱额是多少?
12.如图,在△ABC中,AD为BC边上的高,BC=8,AD=4,点P为边BC上一动点,连接AP,随着BP长度的变化,△ACP的面积也在变化.
(1)在这个变化过程中,自变量是什么?因变量是什么?
(2)若设BP=x,△ACP的面积为y,请写出y与x的关系式;
(3)当BPAD时,求△ACP的面积.
答案解析部分
1.【答案】
【解析】【解答】解:由题意可得2y+x=16,
∴y=-x+8.
故答案为:y=-x+8.
【分析】由题意可得AB+BC+CD=16,即2y+x=16,进而用含x的式子表示出y即可.
2.【答案】-6
【解析】【解答】解:x=-1时,
y=2×(-1)-4=-6
故答案为:-6
【分析】将x=-1代入计算即可。
3.【答案】全体实数
【解析】【解答】解:
∴x可以是任意实数
故答案为:全体实数.
【分析】本题考查函数自变量的取值范围。根据函数的表达式,确定自变量的取值范围。 在一般的函数关系中自变量的取值范围主要考虑以下四种情况:(1)函数关系式为整式形式:自变量取值范围为任意实数;(2)函数关系式为分式形式:分母≠0;(3)函数关系式含算术平方根:被开方数≥0;(4)函数关系式含0指数:底数≠0.
4.【答案】C
【解析】【解答】解:A、B、D都符合函数的定义;
C、对x的一个值y的值不是唯一的,因而不是函数关系.
故答案为:C.
【分析】一般地,在一个变化过程中,如果有两个变量x、y,并且对于x的每一个值,y都有唯一确定的值与其对应,那么我们称y是x的函数,据此逐一判断即可.
5.【答案】B
【解析】【解答】解:观察表格可知楼层n(8≤n<30)每增加1,售价x就增加50元,
所以:x=2000+50(n-8) (8≤n<30),
故答案为:B.
【分析】由表格可知,在8≤n<30范围内,楼层每增加1层,售价就增加50元,所以售价y与楼层n之间成一次函数关系,可设解析式为y=kx+b,再用待定系数法即可求解析式。
6.【答案】D
【解析】【解答】解:A、B、C符合函数的概念,而D中给定一个x值,有两个y值与其对应,故不是函数.
故答案为:D.
【分析】在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,那么就称y是x的函数,据此判断.
7.【答案】B
【解析】【解答】根据题意可得:因变量是水的温度。
故答案为:B。
【分析】利用因变量的定义求解即可。
8.【答案】解:∵四边形ABCD是正方形,
∴∠A=90°,AB=AD=10cm,
∵ 动点M,N同时从点A出发,点M沿AB边向终点B移动,点N沿AD边向终点D移动,速度都是1cm/s,移动的时间是x(s) ,
∴AM=AN=xcm,
∴ △AMN的面积y(cm2)关于x(s)的函数表达式为:,自变量x的取值范围 0≤x≤10.
【解析】【分析】由正方形的性质得∠A=90°,AB=AD=10cm,由路程、速度与时间之间的关系可得AM=AN=xcm,进而根据直角三角形面积计算公式可得y关于x的函数解析式,结合AB及AD的长可得x的取值范围.
9.【答案】解:∵BC=8,CP=x,
∴PB=8﹣x,
∴S△APB=PB AC
=×(8﹣x)×6
=24﹣3x
自变量的取值范围是:0<x<8.
【解析】【分析】由图形可知三角形APB边BP上的高为AC,利用三角形的面积公式表示出y即可得到y与x之间的函数关系式.
10.【答案】(1)解:有可能,理由如下:
∵f= c+32
∴100= c+32
解得c=37.8°,
答:有可能达到100℉.
(2)解:f= c+32
=×15+32
=59 ℃ ,
答: 此地早晨的华氏温度是59℃.
(3)解:∵f= c+32,
∴68= c+32,
解得c=20℃,
答:该时刻摄氏温度是20℃.
【解析】【分析】(1)把f=100℉代入关系式f= c+32求出c值,再和人的正常体温作比较,即可作答;
(2)把c= 15℃代入关系式f= c+32求出f值,即可解答;
(3)把f= 68℉代入关系式f= c+32求出c值,即可解答.
11.【答案】(1)解:卖钱额是随卖出质量的变化而变化,所以质量和卖钱额都是变量,质量是自变量,卖钱额是因变量;
(2)解:y与x之间的关系: y=2x
(3)解:当 时,
即当橘子卖出50千克时,预测卖钱额是100元.
【解析】【分析】(1)在某变化过程中有两个变量x,y,按照某个对应法则,对于给定的x,有唯一确定的值y与之对应,那么y就叫做x的函数。其中x叫自变量,y叫因变量。由表格中的信息和函数的定义可知:卖钱额随卖出的质量的变化而变化,所以可知卖出的质量是自变量,卖钱额是因变量;
(2)由表格中的信息每卖出1千克的橘子,增加2元,所以可得y=2x;
(3)由题意把x=50代入(2)中的解析式计算即可求解。
12.【答案】(1)解:∵ 在这个变化过程中, △ACP的面积随着BP长度的变化而变化,
∴自变量是BP的长,因变量是△ACP的面积.
(2)解:∵BP=x, BC=8,
∴PC=BC-BP=8-x,
∴S△APC=PC·AD
=(8-x)×4
=-2x+16,
即y 与x的关系式为y=-2x+16;
(3)解:∵ BP=AD =2,
∴PC=BC-BP=8-2=6,
∴S△APC=PC·AD
=×6×4
=12.
【解析】【分析】(1)根据△ACP的面积随着BP长度的变化而变化,即可判断出自变量和因变量;
(2)先根据线段间的和差关系用x表示出PC,再表示出△APC的面积,即可解答;
(3)先求出BP长,再根据线段的和差求出PC,再计算△APC的面积,即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
19.1.1 变量与函数
一、填空题
1.学校开设劳动课,规划围成如图所示的长方形ABCD的菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为16米,设BC边的长为x米,AB边的长为y米,则y与x的关系式是 ;(不要求写出自变量的取值范围)
2.函数,则当自变量时, .
3.函数中自变量的取值范围是 .
二、单选题
4.下列各曲线中,不表示y是 x的函数的是( )
A. B.
C. D.
5.新农村社区改造中,有一部分楼盘要对外销售. 某楼共30层,从第八层开始,售价x(元/平方米)与楼层n(8≤n<30)之间的关系如下表:
楼层n 8 9 10 11 12 …
售价x(元/平方米) 2000 2050 2100 2150 2200 …
则售价x(元/平方米)与楼层n之间的关系式为( )
A.x=2000+50n B.x=2000+50(n-8)
C.n=2000+50(x-8) D.n=2000+50x
6.下列关系中,不是函数的是( ).
A.y= B.y=-x2+2x
C.y=9 (x≥0) D.y=±x2
7.利用太阳能热水器加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题的因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水管
三、解答题
8.如图,正方形ABCD的边长为10cm,动点M,N同时从点A出发,点M沿AB边向终点B移动,点N沿AD边向终点D移动,速度都是1cm/s,移动的时间是x(s).求△AMN的面积y(cm2)关于x(s)的函数表达式及自变量x的取值范围.
9.已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
四、综合题
10.华氏温度f(℉)与摄氏温度c(℃)之间存在如下的关系f= c+32.
(1)一个人的体温有可能达到100℉吗(精确到0.1)?
(2)如果某地早晨的摄氏温度为15℃,那么此地早晨的华氏温度是多少?
(3)若当地某一时刻的华氏温度为68℉,则该时刻摄氏温度是多少?
11.下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 1 2 3 4 5 6 7 8 9
卖钱额/元 2 4 6 8 10 12 14 16 18
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;
(3)当橘子卖出50千克时,预测卖钱额是多少?
12.如图,在△ABC中,AD为BC边上的高,BC=8,AD=4,点P为边BC上一动点,连接AP,随着BP长度的变化,△ACP的面积也在变化.
(1)在这个变化过程中,自变量是什么?因变量是什么?
(2)若设BP=x,△ACP的面积为y,请写出y与x的关系式;
(3)当BPAD时,求△ACP的面积.
答案解析部分
1.【答案】
【解析】【解答】解:由题意可得2y+x=16,
∴y=-x+8.
故答案为:y=-x+8.
【分析】由题意可得AB+BC+CD=16,即2y+x=16,进而用含x的式子表示出y即可.
2.【答案】-6
【解析】【解答】解:x=-1时,
y=2×(-1)-4=-6
故答案为:-6
【分析】将x=-1代入计算即可。
3.【答案】全体实数
【解析】【解答】解:
∴x可以是任意实数
故答案为:全体实数.
【分析】本题考查函数自变量的取值范围。根据函数的表达式,确定自变量的取值范围。 在一般的函数关系中自变量的取值范围主要考虑以下四种情况:(1)函数关系式为整式形式:自变量取值范围为任意实数;(2)函数关系式为分式形式:分母≠0;(3)函数关系式含算术平方根:被开方数≥0;(4)函数关系式含0指数:底数≠0.
4.【答案】C
【解析】【解答】解:A、B、D都符合函数的定义;
C、对x的一个值y的值不是唯一的,因而不是函数关系.
故答案为:C.
【分析】一般地,在一个变化过程中,如果有两个变量x、y,并且对于x的每一个值,y都有唯一确定的值与其对应,那么我们称y是x的函数,据此逐一判断即可.
5.【答案】B
【解析】【解答】解:观察表格可知楼层n(8≤n<30)每增加1,售价x就增加50元,
所以:x=2000+50(n-8) (8≤n<30),
故答案为:B.
【分析】由表格可知,在8≤n<30范围内,楼层每增加1层,售价就增加50元,所以售价y与楼层n之间成一次函数关系,可设解析式为y=kx+b,再用待定系数法即可求解析式。
6.【答案】D
【解析】【解答】解:A、B、C符合函数的概念,而D中给定一个x值,有两个y值与其对应,故不是函数.
故答案为:D.
【分析】在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,那么就称y是x的函数,据此判断.
7.【答案】B
【解析】【解答】根据题意可得:因变量是水的温度。
故答案为:B。
【分析】利用因变量的定义求解即可。
8.【答案】解:∵四边形ABCD是正方形,
∴∠A=90°,AB=AD=10cm,
∵ 动点M,N同时从点A出发,点M沿AB边向终点B移动,点N沿AD边向终点D移动,速度都是1cm/s,移动的时间是x(s) ,
∴AM=AN=xcm,
∴ △AMN的面积y(cm2)关于x(s)的函数表达式为:,自变量x的取值范围 0≤x≤10.
【解析】【分析】由正方形的性质得∠A=90°,AB=AD=10cm,由路程、速度与时间之间的关系可得AM=AN=xcm,进而根据直角三角形面积计算公式可得y关于x的函数解析式,结合AB及AD的长可得x的取值范围.
9.【答案】解:∵BC=8,CP=x,
∴PB=8﹣x,
∴S△APB=PB AC
=×(8﹣x)×6
=24﹣3x
自变量的取值范围是:0<x<8.
【解析】【分析】由图形可知三角形APB边BP上的高为AC,利用三角形的面积公式表示出y即可得到y与x之间的函数关系式.
10.【答案】(1)解:有可能,理由如下:
∵f= c+32
∴100= c+32
解得c=37.8°,
答:有可能达到100℉.
(2)解:f= c+32
=×15+32
=59 ℃ ,
答: 此地早晨的华氏温度是59℃.
(3)解:∵f= c+32,
∴68= c+32,
解得c=20℃,
答:该时刻摄氏温度是20℃.
【解析】【分析】(1)把f=100℉代入关系式f= c+32求出c值,再和人的正常体温作比较,即可作答;
(2)把c= 15℃代入关系式f= c+32求出f值,即可解答;
(3)把f= 68℉代入关系式f= c+32求出c值,即可解答.
11.【答案】(1)解:卖钱额是随卖出质量的变化而变化,所以质量和卖钱额都是变量,质量是自变量,卖钱额是因变量;
(2)解:y与x之间的关系: y=2x
(3)解:当 时,
即当橘子卖出50千克时,预测卖钱额是100元.
【解析】【分析】(1)在某变化过程中有两个变量x,y,按照某个对应法则,对于给定的x,有唯一确定的值y与之对应,那么y就叫做x的函数。其中x叫自变量,y叫因变量。由表格中的信息和函数的定义可知:卖钱额随卖出的质量的变化而变化,所以可知卖出的质量是自变量,卖钱额是因变量;
(2)由表格中的信息每卖出1千克的橘子,增加2元,所以可得y=2x;
(3)由题意把x=50代入(2)中的解析式计算即可求解。
12.【答案】(1)解:∵ 在这个变化过程中, △ACP的面积随着BP长度的变化而变化,
∴自变量是BP的长,因变量是△ACP的面积.
(2)解:∵BP=x, BC=8,
∴PC=BC-BP=8-x,
∴S△APC=PC·AD
=(8-x)×4
=-2x+16,
即y 与x的关系式为y=-2x+16;
(3)解:∵ BP=AD =2,
∴PC=BC-BP=8-2=6,
∴S△APC=PC·AD
=×6×4
=12.
【解析】【分析】(1)根据△ACP的面积随着BP长度的变化而变化,即可判断出自变量和因变量;
(2)先根据线段间的和差关系用x表示出PC,再表示出△APC的面积,即可解答;
(3)先求出BP长,再根据线段的和差求出PC,再计算△APC的面积,即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
