19.1 变量与函数综合练习题(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
19.1 变量与函数综合练习题
一、单选题
1.函数 中自变量的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≤3.
2.在国内投寄到外地质量为80g以内的普通信函应付邮资如下表:
信件质量m/g 0<m≤20 20<m≤40 40<m≤60 60<m≤80
邮资y/元 1.20 2.40 3.60 4.80
某同学想寄一封质量为15g的信函给居住在外地的朋友,他应该付的邮资是( )
A.4.80 B.3.60 C.2.40 D.1.20
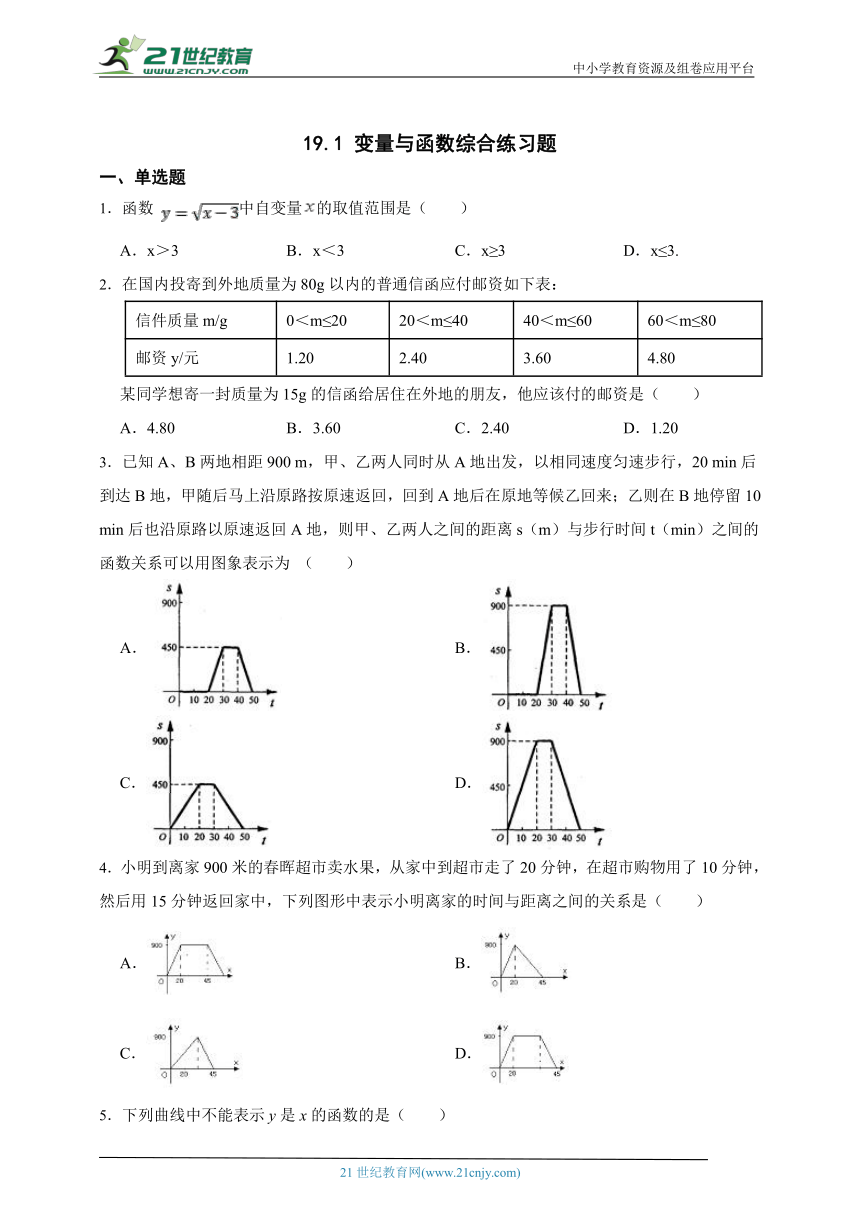
3.已知A、B两地相距900 m,甲、乙两人同时从A地出发,以相同速度匀速步行,20 min后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地停留10 min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)之间的函数关系可以用图象表示为 ( )
A. B.
C. D.
4.小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是( )
A. B.
C. D.
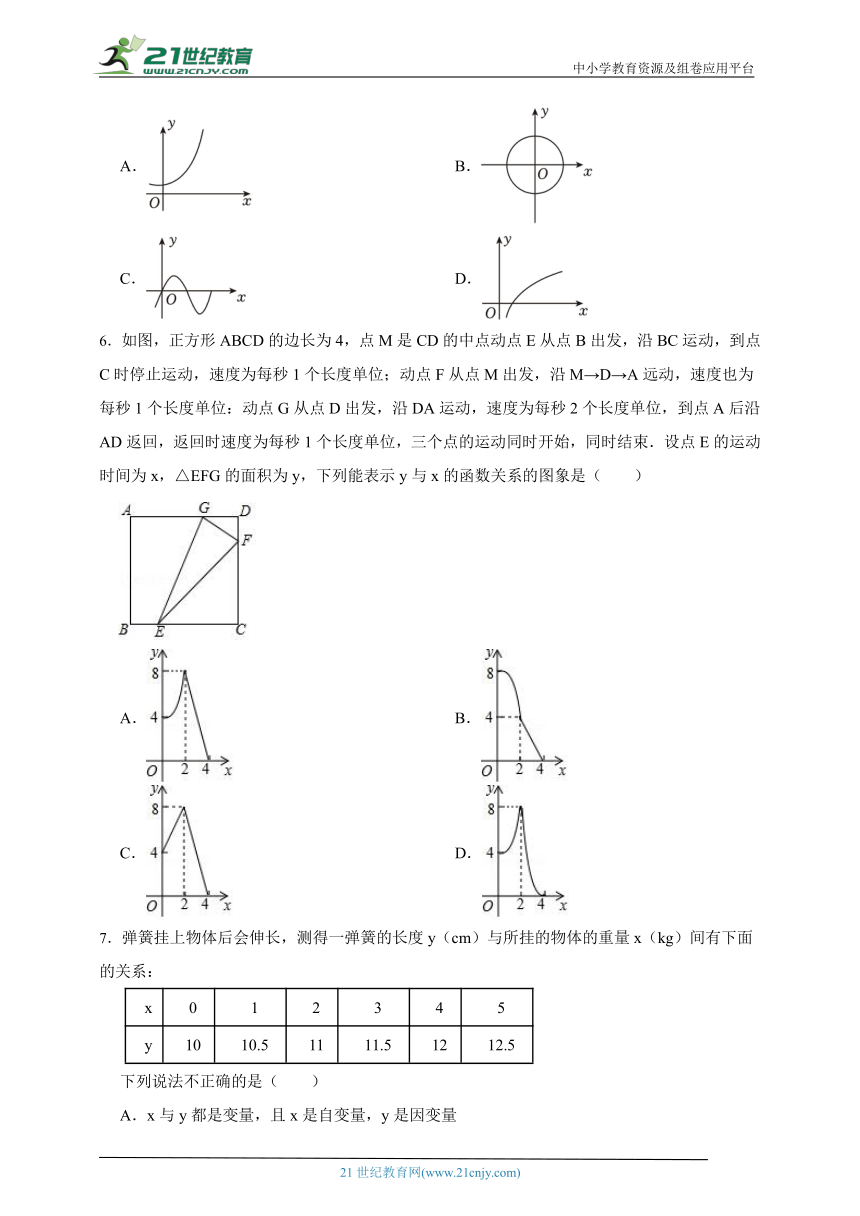
5.下列曲线中不能表示y是x的函数的是( )
A. B.
C. D.
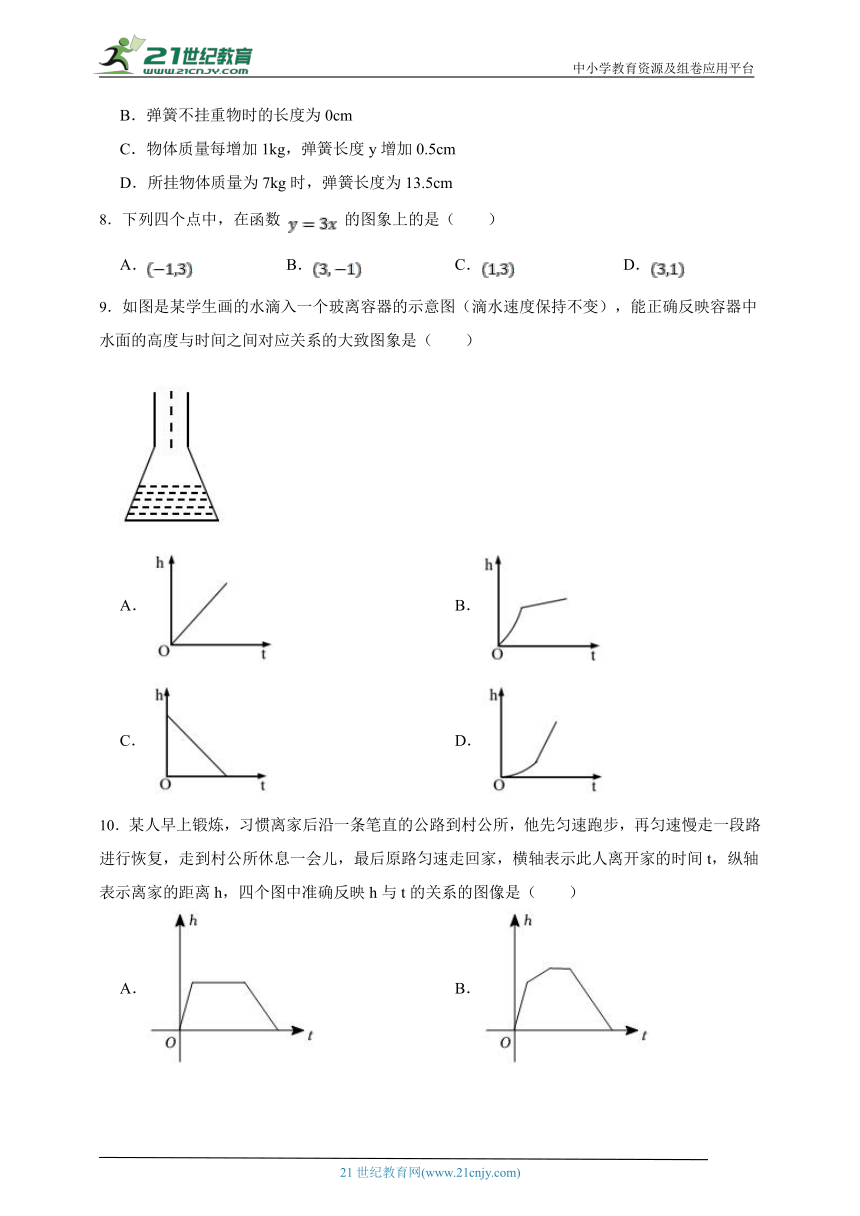
6.如图,正方形ABCD的边长为4,点M是CD的中点动点E从点B出发,沿BC运动,到点C时停止运动,速度为每秒1个长度单位;动点F从点M出发,沿M→D→A远动,速度也为每秒1个长度单位:动点G从点D出发,沿DA运动,速度为每秒2个长度单位,到点A后沿AD返回,返回时速度为每秒1个长度单位,三个点的运动同时开始,同时结束.设点E的运动时间为x,△EFG的面积为y,下列能表示y与x的函数关系的图象是( )
A. B.
C. D.
7.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
8.下列四个点中,在函数 的图象上的是( )
A. B. C. D.
9.如图是某学生画的水滴入一个玻离容器的示意图(滴水速度保持不变),能正确反映容器中水面的高度与时间之间对应关系的大致图象是( )
A. B.
C. D.
10.某人早上锻炼,习惯离家后沿一条笔直的公路到村公所,他先匀速跑步,再匀速慢走一段路进行恢复,走到村公所休息一会儿,最后原路匀速走回家,横轴表示此人离开家的时间t,纵轴表示离家的距离h,四个图中准确反映h与t的关系的图像是( )
A. B.
C. D.
二、填空题
11.根据图中的程序,当输入x=2时,输出结果y= .
12.已知f(x)= ,那么f(1)= .
13.甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是 米.
14.对于实数a和b,定义一种新的运算“*”, ,计算 = .若 恰有三个不相等的实数根 ,记 ,则k的取值范围是 .
三、解答题
15.已知一条钢筋长90cm,把它折弯成一个等腰三角形框,其底边长记为x(cm),腰长记为y(cm).
(1)求y关于x的函数表达式和自变量x的取值范围.
(2)当x=40时,求函数y的值,并求出此时等腰三角形的面积.
16.如图是在固定的电压下,通过一电阻的电流I(A)与该电阻的阻值R(Ω)之间的关系变化图.根据图象回答下列问题:
(1)这个函数反映了哪两个变量之间的关系?
(2)电阻值R是关于电流I的函数吗?
(3)当I=1A时,电阻的阻值是多少?
17.如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发用多长时间就追上甲?
四、作图题
18.有这样一个问题,探究函数y=x2﹣2 的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2 的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2 的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4
y … n 3 0 ﹣1 0 ﹣1 0 3 m
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);
(5)根据图象回答:方程x2﹣2 =﹣ 有 个实数解.
五、综合题
19.已知 与 成正比例,且 时, .
(1)求 与 之间的函数关系式,并建立平面直角坐标系,画出函数图象;
(2)结合图象,当 时,求 的取值范围.
20.(问题情境)
已知矩形的面积为 ( 为常数, ),当该矩形的长为多少时,它的周长最小?最小值是多少?
(数学模型)
设该矩形的长为 ,周长为 ,则 与 的函数表达式为 .
(探索研究)
小彬借鉴以前研究函数的经验,先探索函数 的图象性质.
(1)结合问题情境,函数 的自变量 的取值范围是 ,
下表是 与 的几组对应值.
1 2 3
2
① ▲ ;
②画出该函数图象,结合图象,得出当 ▲ 时, 有最小值, ▲ ;
(2)(解决问题)直接写出“问题情境”中问题的结论.
21.小明在学习函数的过程中遇到这样一个函数:y=[x],若x≥0时,[x]=x2﹣1;若x<0时,[x]=﹣x+1.小明根据学习函数的经验,对该函数进行了探究.
(1)下列关于该函数图象的性质正确的是 ;(填序号)
①y随x的增大而增大;
②该函数图象关于y轴对称;
③当x=0时,函数有最小值为﹣1;
④该函数图象不经过第三象限.
(2)①在平面直角坐标系xOy中画出该函数图象;
②若关于x的方程2x+c=[x]有两个互不相等的实数根,请结合函数图象,直接写出c的取值范围是 ▲ ;
(3)若点(a,b)在函数y=x﹣3图象上,且﹣ <[a]≤2,则b的取值范围是 .
答案解析部分
1.【答案】C
【解析】【分析】根据题意得:x-3≥0,解得:x≥3.故选C.
【点评】本题考查了函数自变量的取值范围的求法,求函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负。
2.【答案】D
【解析】【解答】由题可得,当0<m≤20时,邮资y=1.20元,
∴同学想寄一封质量为15g的信函给居住在外地的朋友,他应该付的邮资是1.20元,
故答案为:D.
【分析】由于0<15g<20,根据表格中的数据即得.
3.【答案】A
【解析】【解答】解:∵甲乙二人乙相同速度匀速步行20 min后从A地到达B地,
∴二人步行的距离为900÷2=450m,
0-20min时,二人同行,距离为0,
20-30min时,甲返回,乙停留在B 地,距离S从0到450m ,
30-40min时,甲继续返回,乙也返回,二人之间的距离保持450m不变,
40-50min时,甲在A地等乙,乙返回,距离S从450到0m,
纵观各选项,只有A选项图象符合.
故答案为:A .
【分析】由题意可得:二人步行的距离为900÷2=450m,0-20min时,二人同行,距离为0;20-30min时,距离S从0到450m;30-40min时,二人之间的距离保持450m不变;40-50min时,距离S从450到0m,据此判断.
4.【答案】D
【解析】【解答】依题意知,y轴代表小明离家距离,x轴代表离家时间,由于中途购物用了10分钟,故y值不变持续了10分钟,可排除BC。而小明往返共用时间45分钟。可选D。
【分析】这是一道分段函数的图象问题,依题意知,y轴代表小明离家距离,x轴代表离家时间,根据中途购物用了10分钟,故y值不变持续了10分钟,由小明往返共用时间45分钟,从而一一排除即可。
5.【答案】B
【解析】【解答】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故B符合题意;
C、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故C不符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意.
故答案为:B.
【分析】在一个变化过程中存在两个变量x、y,对于其中一个变量x的每一个确定的值,另一个变量y都只有唯一 一个值与之对应,于是我们就说y是x的函数,据此逐个判断得出答案.
6.【答案】A
【解析】【解答】解:①当x≤2时,各点位置与原图所示,
此时,BE=x,MF=x,GD=2x,
则y=S△EFG=S正方形ABCD﹣S梯形ABGE﹣S△EFC﹣S△GFD,
将有关数据代入整理得:y=S△EFG=1.5x2﹣x+4,对应图象是二次函数;
②当x>2时,各点位置与下图所示,
此时y=S△EFG= GF AB=﹣4t+16,对应图象是直线,
故答案为:A
【分析】当点F在MD上运动时,0≤x≤2;当点F在DA上运动时,2<x≤4;根据题目中相关图形的面积公式列出表达式进行选择即可。
7.【答案】B
【解析】【解答】解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:B.
【分析】由表中的数据进行分析发现:物体质量每增加1kg,弹簧长度y增加0.5cm;当不挂重物时,弹簧的长度为10cm,然后逐个分析四个选项,得出正确答案.
8.【答案】C
【解析】【解答】解:A、当x=-1, y=-3, 不符合题意;
B、当x=3 y=-9, 不符合题意;
C、当x=1, y=3, 符合题意;
D、当x=3, y=9, 不符合题意.
故答案为:C.
【分析】分别把四个点坐标代入函数式进行验证即可.
9.【答案】D
【解析】【解答】解:由于容器的形状是下宽上窄,所以水的深度上升是先慢后快.
表现出的函数图形为先缓,后陡.
故答案为:D.
【分析】由于容器的形状是下宽上窄,所以水的深度上升是先慢后快,据此逐一判断即可.
10.【答案】B
【解析】【解答】解:由题知,这个人先匀速跑步再匀速慢走,因为匀速跑步比匀速慢走的速度快,所以在相同的时间t内,匀速跑步比匀速慢走对应的h增的多,在图象上,匀速跑步就是比匀速慢走的更陡的线段;走到村公所休息时,说明随着时间t的增大,他离家的距离h不变,在图象上是平行于x轴的线段;最后原路返回家,说明随着时间t的增大,离家的距离h逐渐地变小,最后为0.
故答案为:B.
【分析】由题意可得:开始一段较陡,接下来一段较平缓,休息时为水平的线段,匀速返回时h随着时间t的增大,离家的距离h逐渐变小,直至为0,据此判断.
11.【答案】2
【解析】【解答】∵x=2时,符合x>1的条件,
∴将x=2代入函数y= x+4得:y=2.
故答案为2.
【分析】x=2时,输入x>1的程序,即可得到y的值。
12.【答案】1
【解析】【解答】解:当x=1时,f(1)= =1,
故答案为:1.
【分析】由f(x)= ,将x=1代入计算即可.
13.【答案】87.5
【解析】【解答】解:由题可得,甲从A到达B运动的时间为375秒,
∴甲的速度为:1500÷375=4m/s,
又∵甲乙两人从出发到相遇的时间为200秒,
∴乙的速度为:1500÷200﹣4=3.5m/s,
又∵甲从相遇的地点到达B的路程为:175×4=700米,
乙在两人相遇后运动175秒的路程为:175×3.5=612.5米,
∴甲到B点时,乙距B点的距离为:700﹣612.5=87.5米,
故答案为:87.5
【分析】须审清题意,y轴的含义是二者的距离,因此甲乙两地的距离为1500,200秒相遇,375秒甲到达B地;
14.【答案】;
【解析】【解答】当 时,即 时,
当 时,即 时,
;
设y= ,则y=
其函数图象如图所示,抛物线顶点 ,
根据图象可得:
当 时, 恰有三个不相等的实数根,
其中设 ,为 与 的交点, 为 与 的交点,
,
,
时, ,
故答案为: ;
【分析】分当 时,当 时两种情况,分别代入新定义的运算算式即可求解;设y= ,绘制其函数图象,根据图象确定m的取值范围,再求k的取值范围.
15.【答案】(1)由已知,得x+2y=90,x>0,2y>x.
整理,得.
∴y关于x的函数表达式是,
自变量x的取值范围是0(2)当x=40时,,
此时底边上的高为,
∴等腰三角形的面积是.
16.【答案】(1)解:根据题意可知 这个函数反映了R,I两个变量之间的关系.
(2)解:∵电阻值R随着电流I的变化而变化,
∴电阻值R是关于电流I的函数.
(3)解:由图象可知RI=16,
∴当I=1A时R=16Ω,
∴当I=1A时,电阻的阻值是16Ω.
【解析】【分析】(1)利用函数图象可得到两个变量.
(2)利用图象可知电阻值R随着电流I的变化而变化,据此可作出判断.
(3)由图象可知RI=16,即可求出当I=1A时R的值.
17.【答案】(1)解:甲下午1时出发,乙下午2时出发,
所以甲更早,早出发1小时
(2)解:甲5时到达,乙3时到达,
所以乙更早,早到2小时
(3)解:乙的速度= =50(千米/小时),
甲的平均速度= =12.5(千米/小时)
(4)解:设乙出发x小时就追上甲,
根据题意得:50x=20+10x,
x=0.5,
答:乙出发0.5小时就追上甲
【解析】【分析】(1)(2)读图可知;(3)从图中得:甲和乙所走的路程都是50千米,甲一共用了4小时,乙一共用了1小时,根据速度= ,代入计算得出;(4)从图中得:甲在走完全程时,前1小时速度为20千米/小时,从第2小时开始,速度为 =10千米/小时,因此设乙出发x小时就追上甲,则从图中看,是在甲速度为10千米/小时时与乙相遇,所以甲的路程为20+10x,乙的路程为50x,列方程解出即可.
18.【答案】(1)自变量取值范围是任意实数
(2)解:当x=4时,y= .
答:m的值为8.
(3)解:如图:
(4)解:根据函数图象可知:
当x<﹣1时,y随x的增大而减小.
(5)3
【解析】【解答】解:(1)根据函数解析式可知:无论x为何值, 均有意义,
∴自变量取值范围是任意实数.
故答案为任意实数.(5)解:根据图象可知:
直线y=﹣ ,与函数图象有三个交点,即可得:
方程x2﹣2 =﹣ 有3个实数解.
【分析】(1)根据二次根式的意义和函数关系式即可求解;(2)根据函数关系式将x的值代入即可求解;(3)根据表格数据,描点,连线,即可画出图象;(4)观察函数图象,利用增减性写出一条性质;(5)根据图象将y=x2-2 的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
19.【答案】(1)解:∵ 与 成正比例,
∴设y=k(x+2),
∵x=1时,y= 6.
∴ 6=k(1+2)
k= 2.
∴y= 2(x+2)= 2x 4
故 与 之间的函数关系式为:
y= 2x 4.
当x=0时,y=-4;
当y=0时,x=-2;
∴图象过点(0, 4)和( 2,0)
故图像如图所示:
;
(2)解:由图像及解析式得:
当y=0时,x=-2
当y=-2时,x=-1
故当 2<y≤0时,
x的取值范围 2≤x< 1.
【解析】【分析】(1)根据y与x+2成正比例,且x=1时,y=-6可确定解析式并能画出图象;
(2)根据图象和y的取值范围可求出x的取值范围。
20.【答案】(1)解:① 4;②函数图象如图:
;1|2
(2)解:当矩形的长为 时,它的周长最小,最小值是 .
【解析】【解答】解:(1)①令y= ,则 ,解得x=4;故填4;
②函数图象如图:
∵ ,
∴ ≥0
∴当x=1,函数的最小值为2;
(2)∵
∴当矩形的长为 时,它的周长最小,最小值是 .
【分析】(1)①令y= ,则 ,解得x=4,即m=4;
②利用描点、连线可画出函数的图象,y=x+=+2,x>0,根据平方的非负性可得y的最小值;
(2) ,同理可得y的最小值.
21.【答案】(1)③④
(2)解:①在平面直角坐标系 中画出该函数图象,
;②c>1或-2<c≤-1
(3)-4≤b<-3或
【解析】【解答】解:(1)画出图象,根据图象可知,
①当 时, y随x的增大而增大,故错误;
②该函数图象关于y轴不对称,故错误;
③当 时,函数有最小值为 ,正确;
④该函数图象不经过第三象限,正确;
故答案为:③④.
(2)② 关于x的方程 有两个互不相等的实数根,
可以看成是 和 有两个交点.
是一次函数,与y轴的交点为c ,
当 c>1 时,满足两个交点的条件.
若将 向下平移与图象有两个交点,则 .
方程为 ,即 .
△ ,
,
.
故答案为: 或 .
(3) ,
当 时, , ,解出 .
当 时, , ,解出 .
或 .
点 在函数 图象上,
,
,
或 .
故答案为: 或 .
【分析】(1)画出函数图象,结合图象根据函数的性质即可判断求解;
(2)①根据题意列表、描点、连线即可画出函数图象;
②将2x+c看成是一次函数y=2x+c,此函数与y轴的交点是c,因此要与[x]图象有两个交点,由题意可分情况讨论:当c>1时,满足两个交点的要求;若将y=2x+c向下平移与图象有两个交点,则 ,方程为 ,即 ,根据根的判别式求出c的范围即可;
(3)因为 <[a]≤2,所以根据分段函数图象,求解取值在 到2之间的自变量的范围,分情况讨论即可.再根据点(a,b)在函数y=x 3图象上,则b=a 3,即a=b+3,代入到a的取值范围中求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
19.1 变量与函数综合练习题
一、单选题
1.函数 中自变量的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≤3.
2.在国内投寄到外地质量为80g以内的普通信函应付邮资如下表:
信件质量m/g 0<m≤20 20<m≤40 40<m≤60 60<m≤80
邮资y/元 1.20 2.40 3.60 4.80
某同学想寄一封质量为15g的信函给居住在外地的朋友,他应该付的邮资是( )
A.4.80 B.3.60 C.2.40 D.1.20
3.已知A、B两地相距900 m,甲、乙两人同时从A地出发,以相同速度匀速步行,20 min后到达B地,甲随后马上沿原路按原速返回,回到A地后在原地等候乙回来;乙则在B地停留10 min后也沿原路以原速返回A地,则甲、乙两人之间的距离s(m)与步行时间t(min)之间的函数关系可以用图象表示为 ( )
A. B.
C. D.
4.小明到离家900米的春晖超市卖水果,从家中到超市走了20分钟,在超市购物用了10分钟,然后用15分钟返回家中,下列图形中表示小明离家的时间与距离之间的关系是( )
A. B.
C. D.
5.下列曲线中不能表示y是x的函数的是( )
A. B.
C. D.
6.如图,正方形ABCD的边长为4,点M是CD的中点动点E从点B出发,沿BC运动,到点C时停止运动,速度为每秒1个长度单位;动点F从点M出发,沿M→D→A远动,速度也为每秒1个长度单位:动点G从点D出发,沿DA运动,速度为每秒2个长度单位,到点A后沿AD返回,返回时速度为每秒1个长度单位,三个点的运动同时开始,同时结束.设点E的运动时间为x,△EFG的面积为y,下列能表示y与x的函数关系的图象是( )
A. B.
C. D.
7.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x 0 1 2 3 4 5
y 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0cm
C.物体质量每增加1kg,弹簧长度y增加0.5cm
D.所挂物体质量为7kg时,弹簧长度为13.5cm
8.下列四个点中,在函数 的图象上的是( )
A. B. C. D.
9.如图是某学生画的水滴入一个玻离容器的示意图(滴水速度保持不变),能正确反映容器中水面的高度与时间之间对应关系的大致图象是( )
A. B.
C. D.
10.某人早上锻炼,习惯离家后沿一条笔直的公路到村公所,他先匀速跑步,再匀速慢走一段路进行恢复,走到村公所休息一会儿,最后原路匀速走回家,横轴表示此人离开家的时间t,纵轴表示离家的距离h,四个图中准确反映h与t的关系的图像是( )
A. B.
C. D.
二、填空题
11.根据图中的程序,当输入x=2时,输出结果y= .
12.已知f(x)= ,那么f(1)= .
13.甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是 米.
14.对于实数a和b,定义一种新的运算“*”, ,计算 = .若 恰有三个不相等的实数根 ,记 ,则k的取值范围是 .
三、解答题
15.已知一条钢筋长90cm,把它折弯成一个等腰三角形框,其底边长记为x(cm),腰长记为y(cm).
(1)求y关于x的函数表达式和自变量x的取值范围.
(2)当x=40时,求函数y的值,并求出此时等腰三角形的面积.
16.如图是在固定的电压下,通过一电阻的电流I(A)与该电阻的阻值R(Ω)之间的关系变化图.根据图象回答下列问题:
(1)这个函数反映了哪两个变量之间的关系?
(2)电阻值R是关于电流I的函数吗?
(3)当I=1A时,电阻的阻值是多少?
17.如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发用多长时间就追上甲?
四、作图题
18.有这样一个问题,探究函数y=x2﹣2 的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2 的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2 的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4
y … n 3 0 ﹣1 0 ﹣1 0 3 m
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);
(5)根据图象回答:方程x2﹣2 =﹣ 有 个实数解.
五、综合题
19.已知 与 成正比例,且 时, .
(1)求 与 之间的函数关系式,并建立平面直角坐标系,画出函数图象;
(2)结合图象,当 时,求 的取值范围.
20.(问题情境)
已知矩形的面积为 ( 为常数, ),当该矩形的长为多少时,它的周长最小?最小值是多少?
(数学模型)
设该矩形的长为 ,周长为 ,则 与 的函数表达式为 .
(探索研究)
小彬借鉴以前研究函数的经验,先探索函数 的图象性质.
(1)结合问题情境,函数 的自变量 的取值范围是 ,
下表是 与 的几组对应值.
1 2 3
2
① ▲ ;
②画出该函数图象,结合图象,得出当 ▲ 时, 有最小值, ▲ ;
(2)(解决问题)直接写出“问题情境”中问题的结论.
21.小明在学习函数的过程中遇到这样一个函数:y=[x],若x≥0时,[x]=x2﹣1;若x<0时,[x]=﹣x+1.小明根据学习函数的经验,对该函数进行了探究.
(1)下列关于该函数图象的性质正确的是 ;(填序号)
①y随x的增大而增大;
②该函数图象关于y轴对称;
③当x=0时,函数有最小值为﹣1;
④该函数图象不经过第三象限.
(2)①在平面直角坐标系xOy中画出该函数图象;
②若关于x的方程2x+c=[x]有两个互不相等的实数根,请结合函数图象,直接写出c的取值范围是 ▲ ;
(3)若点(a,b)在函数y=x﹣3图象上,且﹣ <[a]≤2,则b的取值范围是 .
答案解析部分
1.【答案】C
【解析】【分析】根据题意得:x-3≥0,解得:x≥3.故选C.
【点评】本题考查了函数自变量的取值范围的求法,求函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负。
2.【答案】D
【解析】【解答】由题可得,当0<m≤20时,邮资y=1.20元,
∴同学想寄一封质量为15g的信函给居住在外地的朋友,他应该付的邮资是1.20元,
故答案为:D.
【分析】由于0<15g<20,根据表格中的数据即得.
3.【答案】A
【解析】【解答】解:∵甲乙二人乙相同速度匀速步行20 min后从A地到达B地,
∴二人步行的距离为900÷2=450m,
0-20min时,二人同行,距离为0,
20-30min时,甲返回,乙停留在B 地,距离S从0到450m ,
30-40min时,甲继续返回,乙也返回,二人之间的距离保持450m不变,
40-50min时,甲在A地等乙,乙返回,距离S从450到0m,
纵观各选项,只有A选项图象符合.
故答案为:A .
【分析】由题意可得:二人步行的距离为900÷2=450m,0-20min时,二人同行,距离为0;20-30min时,距离S从0到450m;30-40min时,二人之间的距离保持450m不变;40-50min时,距离S从450到0m,据此判断.
4.【答案】D
【解析】【解答】依题意知,y轴代表小明离家距离,x轴代表离家时间,由于中途购物用了10分钟,故y值不变持续了10分钟,可排除BC。而小明往返共用时间45分钟。可选D。
【分析】这是一道分段函数的图象问题,依题意知,y轴代表小明离家距离,x轴代表离家时间,根据中途购物用了10分钟,故y值不变持续了10分钟,由小明往返共用时间45分钟,从而一一排除即可。
5.【答案】B
【解析】【解答】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故B符合题意;
C、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故C不符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意.
故答案为:B.
【分析】在一个变化过程中存在两个变量x、y,对于其中一个变量x的每一个确定的值,另一个变量y都只有唯一 一个值与之对应,于是我们就说y是x的函数,据此逐个判断得出答案.
6.【答案】A
【解析】【解答】解:①当x≤2时,各点位置与原图所示,
此时,BE=x,MF=x,GD=2x,
则y=S△EFG=S正方形ABCD﹣S梯形ABGE﹣S△EFC﹣S△GFD,
将有关数据代入整理得:y=S△EFG=1.5x2﹣x+4,对应图象是二次函数;
②当x>2时,各点位置与下图所示,
此时y=S△EFG= GF AB=﹣4t+16,对应图象是直线,
故答案为:A
【分析】当点F在MD上运动时,0≤x≤2;当点F在DA上运动时,2<x≤4;根据题目中相关图形的面积公式列出表达式进行选择即可。
7.【答案】B
【解析】【解答】解:A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B、弹簧不挂重物时的长度为10cm,故B选项错误;
C、物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D、由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确;
故选:B.
【分析】由表中的数据进行分析发现:物体质量每增加1kg,弹簧长度y增加0.5cm;当不挂重物时,弹簧的长度为10cm,然后逐个分析四个选项,得出正确答案.
8.【答案】C
【解析】【解答】解:A、当x=-1, y=-3, 不符合题意;
B、当x=3 y=-9, 不符合题意;
C、当x=1, y=3, 符合题意;
D、当x=3, y=9, 不符合题意.
故答案为:C.
【分析】分别把四个点坐标代入函数式进行验证即可.
9.【答案】D
【解析】【解答】解:由于容器的形状是下宽上窄,所以水的深度上升是先慢后快.
表现出的函数图形为先缓,后陡.
故答案为:D.
【分析】由于容器的形状是下宽上窄,所以水的深度上升是先慢后快,据此逐一判断即可.
10.【答案】B
【解析】【解答】解:由题知,这个人先匀速跑步再匀速慢走,因为匀速跑步比匀速慢走的速度快,所以在相同的时间t内,匀速跑步比匀速慢走对应的h增的多,在图象上,匀速跑步就是比匀速慢走的更陡的线段;走到村公所休息时,说明随着时间t的增大,他离家的距离h不变,在图象上是平行于x轴的线段;最后原路返回家,说明随着时间t的增大,离家的距离h逐渐地变小,最后为0.
故答案为:B.
【分析】由题意可得:开始一段较陡,接下来一段较平缓,休息时为水平的线段,匀速返回时h随着时间t的增大,离家的距离h逐渐变小,直至为0,据此判断.
11.【答案】2
【解析】【解答】∵x=2时,符合x>1的条件,
∴将x=2代入函数y= x+4得:y=2.
故答案为2.
【分析】x=2时,输入x>1的程序,即可得到y的值。
12.【答案】1
【解析】【解答】解:当x=1时,f(1)= =1,
故答案为:1.
【分析】由f(x)= ,将x=1代入计算即可.
13.【答案】87.5
【解析】【解答】解:由题可得,甲从A到达B运动的时间为375秒,
∴甲的速度为:1500÷375=4m/s,
又∵甲乙两人从出发到相遇的时间为200秒,
∴乙的速度为:1500÷200﹣4=3.5m/s,
又∵甲从相遇的地点到达B的路程为:175×4=700米,
乙在两人相遇后运动175秒的路程为:175×3.5=612.5米,
∴甲到B点时,乙距B点的距离为:700﹣612.5=87.5米,
故答案为:87.5
【分析】须审清题意,y轴的含义是二者的距离,因此甲乙两地的距离为1500,200秒相遇,375秒甲到达B地;
14.【答案】;
【解析】【解答】当 时,即 时,
当 时,即 时,
;
设y= ,则y=
其函数图象如图所示,抛物线顶点 ,
根据图象可得:
当 时, 恰有三个不相等的实数根,
其中设 ,为 与 的交点, 为 与 的交点,
,
,
时, ,
故答案为: ;
【分析】分当 时,当 时两种情况,分别代入新定义的运算算式即可求解;设y= ,绘制其函数图象,根据图象确定m的取值范围,再求k的取值范围.
15.【答案】(1)由已知,得x+2y=90,x>0,2y>x.
整理,得.
∴y关于x的函数表达式是,
自变量x的取值范围是0
此时底边上的高为,
∴等腰三角形的面积是.
16.【答案】(1)解:根据题意可知 这个函数反映了R,I两个变量之间的关系.
(2)解:∵电阻值R随着电流I的变化而变化,
∴电阻值R是关于电流I的函数.
(3)解:由图象可知RI=16,
∴当I=1A时R=16Ω,
∴当I=1A时,电阻的阻值是16Ω.
【解析】【分析】(1)利用函数图象可得到两个变量.
(2)利用图象可知电阻值R随着电流I的变化而变化,据此可作出判断.
(3)由图象可知RI=16,即可求出当I=1A时R的值.
17.【答案】(1)解:甲下午1时出发,乙下午2时出发,
所以甲更早,早出发1小时
(2)解:甲5时到达,乙3时到达,
所以乙更早,早到2小时
(3)解:乙的速度= =50(千米/小时),
甲的平均速度= =12.5(千米/小时)
(4)解:设乙出发x小时就追上甲,
根据题意得:50x=20+10x,
x=0.5,
答:乙出发0.5小时就追上甲
【解析】【分析】(1)(2)读图可知;(3)从图中得:甲和乙所走的路程都是50千米,甲一共用了4小时,乙一共用了1小时,根据速度= ,代入计算得出;(4)从图中得:甲在走完全程时,前1小时速度为20千米/小时,从第2小时开始,速度为 =10千米/小时,因此设乙出发x小时就追上甲,则从图中看,是在甲速度为10千米/小时时与乙相遇,所以甲的路程为20+10x,乙的路程为50x,列方程解出即可.
18.【答案】(1)自变量取值范围是任意实数
(2)解:当x=4时,y= .
答:m的值为8.
(3)解:如图:
(4)解:根据函数图象可知:
当x<﹣1时,y随x的增大而减小.
(5)3
【解析】【解答】解:(1)根据函数解析式可知:无论x为何值, 均有意义,
∴自变量取值范围是任意实数.
故答案为任意实数.(5)解:根据图象可知:
直线y=﹣ ,与函数图象有三个交点,即可得:
方程x2﹣2 =﹣ 有3个实数解.
【分析】(1)根据二次根式的意义和函数关系式即可求解;(2)根据函数关系式将x的值代入即可求解;(3)根据表格数据,描点,连线,即可画出图象;(4)观察函数图象,利用增减性写出一条性质;(5)根据图象将y=x2-2 的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
19.【答案】(1)解:∵ 与 成正比例,
∴设y=k(x+2),
∵x=1时,y= 6.
∴ 6=k(1+2)
k= 2.
∴y= 2(x+2)= 2x 4
故 与 之间的函数关系式为:
y= 2x 4.
当x=0时,y=-4;
当y=0时,x=-2;
∴图象过点(0, 4)和( 2,0)
故图像如图所示:
;
(2)解:由图像及解析式得:
当y=0时,x=-2
当y=-2时,x=-1
故当 2<y≤0时,
x的取值范围 2≤x< 1.
【解析】【分析】(1)根据y与x+2成正比例,且x=1时,y=-6可确定解析式并能画出图象;
(2)根据图象和y的取值范围可求出x的取值范围。
20.【答案】(1)解:① 4;②函数图象如图:
;1|2
(2)解:当矩形的长为 时,它的周长最小,最小值是 .
【解析】【解答】解:(1)①令y= ,则 ,解得x=4;故填4;
②函数图象如图:
∵ ,
∴ ≥0
∴当x=1,函数的最小值为2;
(2)∵
∴当矩形的长为 时,它的周长最小,最小值是 .
【分析】(1)①令y= ,则 ,解得x=4,即m=4;
②利用描点、连线可画出函数的图象,y=x+=+2,x>0,根据平方的非负性可得y的最小值;
(2) ,同理可得y的最小值.
21.【答案】(1)③④
(2)解:①在平面直角坐标系 中画出该函数图象,
;②c>1或-2<c≤-1
(3)-4≤b<-3或
【解析】【解答】解:(1)画出图象,根据图象可知,
①当 时, y随x的增大而增大,故错误;
②该函数图象关于y轴不对称,故错误;
③当 时,函数有最小值为 ,正确;
④该函数图象不经过第三象限,正确;
故答案为:③④.
(2)② 关于x的方程 有两个互不相等的实数根,
可以看成是 和 有两个交点.
是一次函数,与y轴的交点为c ,
当 c>1 时,满足两个交点的条件.
若将 向下平移与图象有两个交点,则 .
方程为 ,即 .
△ ,
,
.
故答案为: 或 .
(3) ,
当 时, , ,解出 .
当 时, , ,解出 .
或 .
点 在函数 图象上,
,
,
或 .
故答案为: 或 .
【分析】(1)画出函数图象,结合图象根据函数的性质即可判断求解;
(2)①根据题意列表、描点、连线即可画出函数图象;
②将2x+c看成是一次函数y=2x+c,此函数与y轴的交点是c,因此要与[x]图象有两个交点,由题意可分情况讨论:当c>1时,满足两个交点的要求;若将y=2x+c向下平移与图象有两个交点,则 ,方程为 ,即 ,根据根的判别式求出c的范围即可;
(3)因为 <[a]≤2,所以根据分段函数图象,求解取值在 到2之间的自变量的范围,分情况讨论即可.再根据点(a,b)在函数y=x 3图象上,则b=a 3,即a=b+3,代入到a的取值范围中求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
