19.2.3一次函数与方程、不等式同步练习(含解析)
文档属性
| 名称 | 19.2.3一次函数与方程、不等式同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.2.3一次函数与方程、不等式
一、填空题
1.如图:点在直线上,则不等式关于的解集是 .
2.若直线y=kx+3的图象经过点(2,0),则关于x的不等式kx+3>0的解集是 .
3.已知一次函数 与 图象如图所示,则下列结论:① ;② ;③关于 的方程 的解为 ;④当 , .其中正确的有 (填序号).
4.一次函数y=-2x+4与x轴的交点坐标是 。
二、单选题
5.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( )
A. B. C. D.
6.若函数 的图象如图所示,则关于 的不等式 的解集为( )
A. B. C. D.
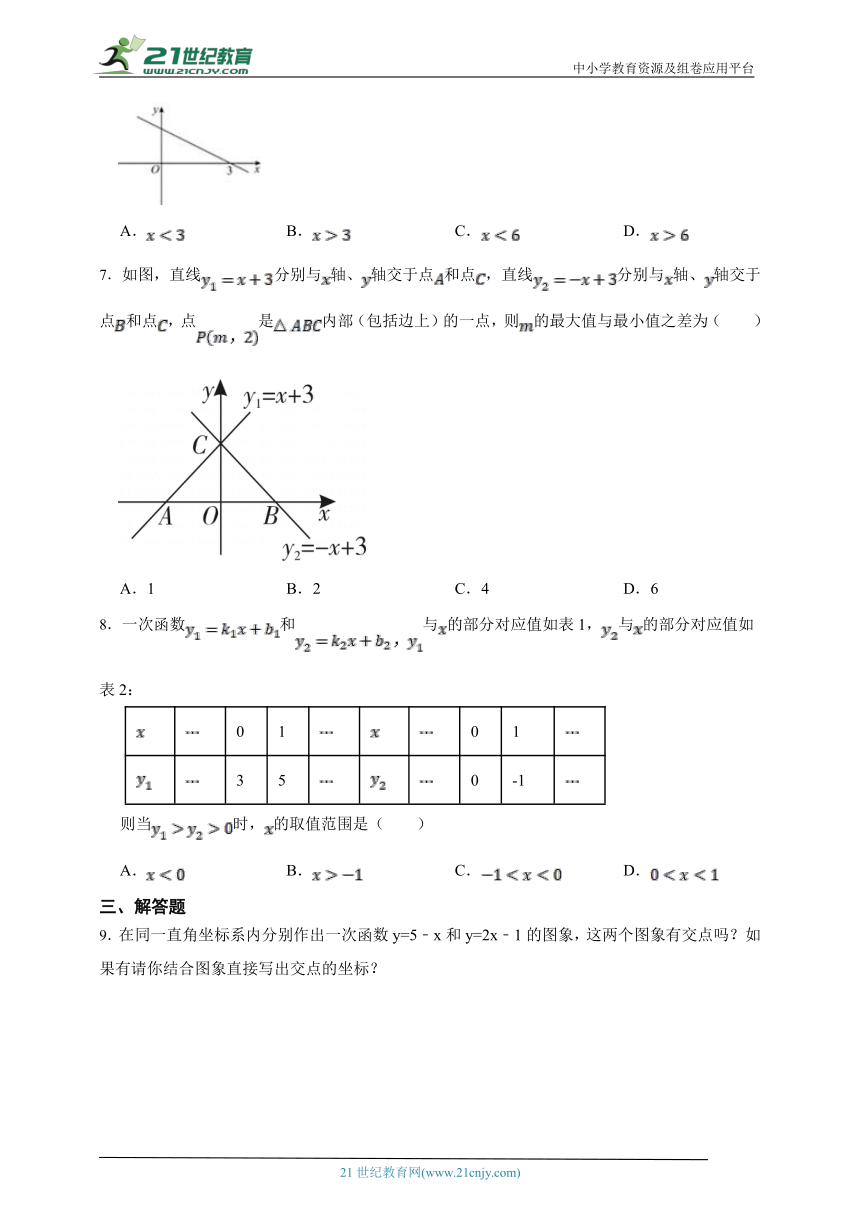
7.如图,直线分别与轴、轴交于点和点,直线分别与轴、轴交于点和点,点是内部(包括边上)的一点,则的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
8.一次函数和与的部分对应值如表1,与的部分对应值如表2:
0 1 0 1
3 5 0 -1
则当时,的取值范围是( )
A. B. C. D.
三、解答题
9.在同一直角坐标系内分别作出一次函数y=5﹣x和y=2x﹣1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?
四、综合题
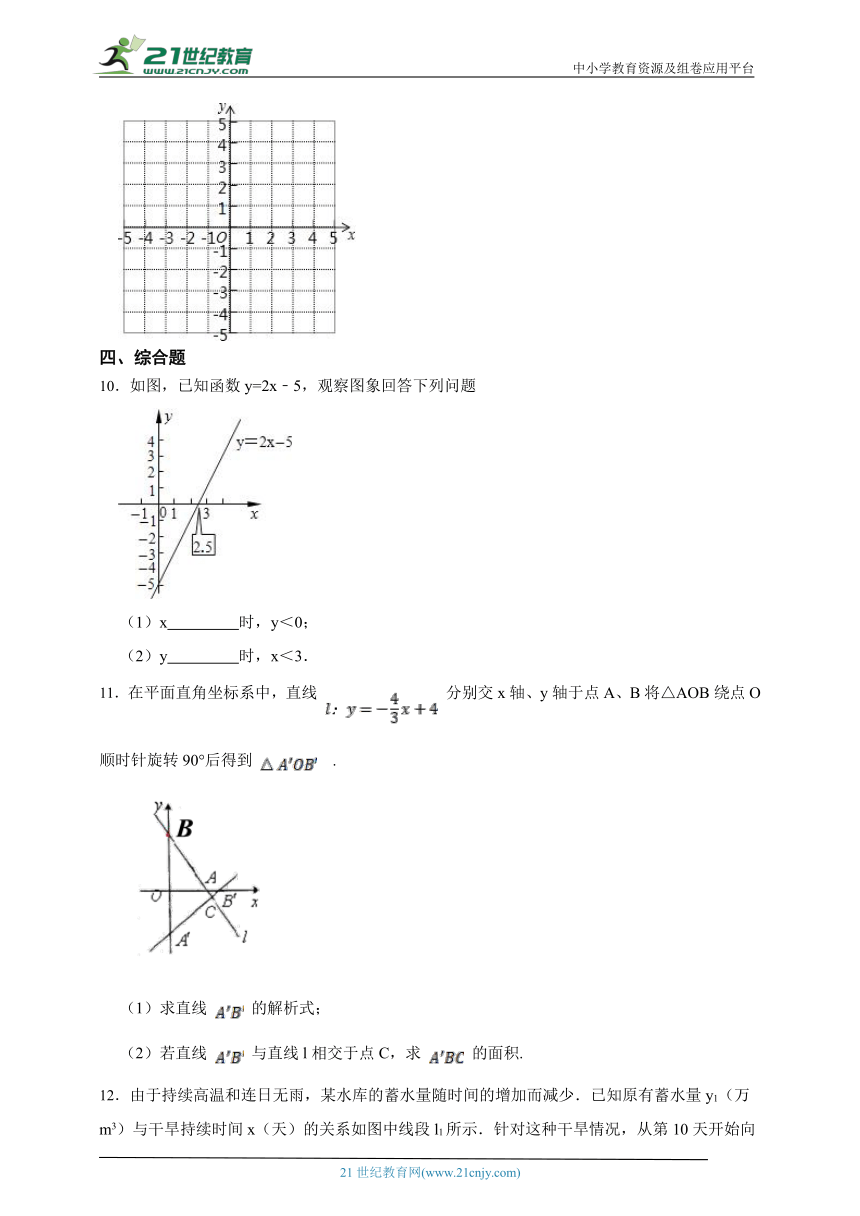
10.如图,已知函数y=2x﹣5,观察图象回答下列问题
(1)x 时,y<0;
(2)y 时,x<3.
11.在平面直角坐标系中,直线 分别交x轴、y轴于点A、B将△AOB绕点O顺时针旋转90°后得到 .
(1)求直线 的解析式;
(2)若直线 与直线l相交于点C,求 的面积.
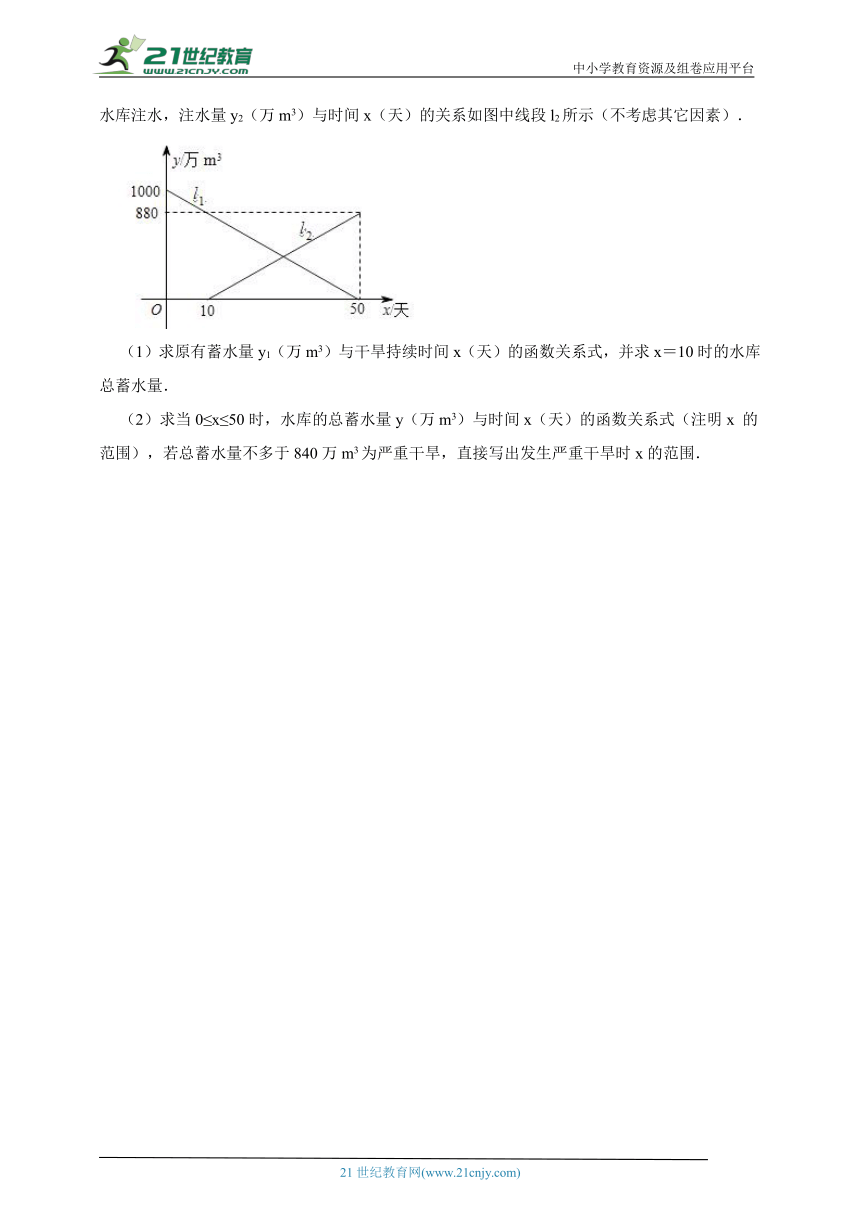
12.由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少.已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示.针对这种干旱情况,从第10天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
(1)求原有蓄水量y1(万m3)与干旱持续时间x(天)的函数关系式,并求x=10时的水库总蓄水量.
(2)求当0≤x≤50时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x 的范围),若总蓄水量不多于840万m3为严重干旱,直接写出发生严重干旱时x的范围.
答案解析部分
1.【答案】
【解析】【解答】
方法1:
点在直线上∴ y=3时,x=-2
由图分析可知,当,x≤-2
方法2:
∵ 点在直线上
∴ -2k+b=3
∴ b=3+2k
∴ kx+3+2k≥3
∴ kx+2k≥0
∴ k(x+2)≥0
∴ x+2≤0
即 x≤-2
【分析】本题考查一次函数与一元一次不等式的关系。 利用一次函数图象解一元一次不等式要先找线,由y的范围确定图象,对应的横坐标x的取值范围就是一元一次不等式的解集。或者点在函数上,得到b的代数式,再代入求不等式的解集也可。
2.【答案】
【解析】【解答】解:∵直线y=kx+3的图象经过点(2,0),
∴0=2k+3,
解得k=- ,
则不等式kx+3>0为- x+3>0,
解得:x<2,
故答案为:x<2.
【分析】把点(2,0)代入解析式,利用待定系数法求出k的值,然后再解不等式即可.
3.【答案】③④
【解析】【解答】解:∵一次函数y1=kx+b经过第一、二、四象限,
∴k<0,b>0,所以①错误;
∵直线y2=x+a的图象与y轴的交点在x轴下方,
∴a<0,所以②错误;
∵一次函数y1=kx+b与y2=x+a的图象的交点的横坐标为3,
∴x=3时,kx+b=x﹣a,所以③正确;
当x>3时,y1<y2,所以④正确.
故答案为 :③④.
【分析】根据一次函数的图象、系数与性质对①②进行判断;利用一次函数与一元一次方程的关系对③进行判断;利用函数图象,当x>3时,一次函数y1=kx+b在直线y2=x+a的下方,则可对④进行判断.
4.【答案】(2,0)
【解析】【解答】解:当y=0时-2x+4=0
解之:x=2
∴交点坐标为:(2,0).
故答案为:(2,0).
【分析】由y=0建立关于x的方程,解方程求出x的值,即可得到一次函数图象与x轴的交点坐标。
5.【答案】B
【解析】【解答】解:∵函数y=ax+b和y=kx的图象交于点P的坐标为(-4,-2),
∴关于x,y的二元一次方程组的解是.
故答案为:B.
【分析】结合函数图象,利用两函数图象的交点坐标即是二元一次方程组的解求解即可。
6.【答案】B
【解析】【解答】解:由函数图象可得一次函数y=kx+b经过点(3,0),
∴当x>3时,y=kx+b<0,
故答案为:B.
【分析】由图知,直线与x轴的交点式(3,0),而不等式kx+b<0即是直线在x轴的下方的部分,其对应的x的值在3的右边部分,所以可得不等式的解集为x>3。
7.【答案】B
【解析】【解答】 解:点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示,
当P为直线y=2与直线y2的交点时,m取最大值,
当P为直线y=2与直线y1的交点时,m取最小值,
∵y1=-x+3中令y=2,则x=1,
y2=x+3中令y=2,则x=-1,
∴m的最大值为1,m的最小值为-1.
则m的最大值与最小值之差为:1-(-1)=2
故选:B.
【分析】 根据一次函数的性质,因为P的纵坐标为2,故点P在直线y=2上,则P点位于两条边上即可得到最值,当P点位于y2上时m有最小值,当P点位于y1上时m有最大值,故可求得.
8.【答案】C
【解析】【解答】解:将(0,3)、(1,5)代入y1=k1x+b1中可得
解得,
∴y1=2x+3.
将(0,0)、(1,-1)代入y2=k2x+b2中可得
解得,
∴y2=-x.
联立y1=2x+3、y2=-x可得,
∴当y1>y2>0时,-1故答案为:C.
【分析】利用待定系数法求出y1、y2,联立求出两一次函数图象的交点坐标,据此解答.
9.【答案】解:如图,
根据图象得到交点坐标为(2,3)
【解析】【分析】首先利用两点法作图作出两个函数的图象,即可得出交点坐标.
10.【答案】(1)<2.5
(2)<1
【解析】【解答】解:(1)当x<2.5时,y<0;
2)当x=3时,y=2x﹣5=1,
所以y<1时,x<3.
故答案为<2.5,<1.
【分析】(1)写出函数图象在x轴下方所对应的自变量的取值范围即可;(2)先计算出自变量为3所对应的函数值,然后利用图象和判断x<3时所对应的函数值的范围.
11.【答案】(1)解:由直线l: 分别交x轴,y轴于点A、B.可知:A(3,0),B(0,4).∵△AOB绕点O顺时针旋转90°而得到△A′OB′,∴△AOB≌△A′OB′,故A′(0,﹣3),B′(4,0).设直线A′B′的解析式为y=kx+b(k≠0,k,b为常数)
∴ ,解得: ,∴直线A′B′的解析式为
(2)解:由题意得: ,解得: ,∴C( ,﹣ ),又A′B=3+4=7,∴S△A′BC= =
【解析】【分析】(1)首先根据坐标轴上点的坐标特点,求出A,B两点的坐标,由于△AOB绕点O顺时针旋转90°而得到△A′OB′,根据旋转的性质△AOB≌△A′OB′,从而得出A′,B′的坐标,再用待定系数法,求出直线A′B′的解析式;
(2)解直线A′B′的解析式与直线l的解析式联立的方程组,得出C点的坐标,然后根据三角形的面积公式得出答案。
12.【答案】(1)解:设 ,把(0,1000),(50,0)代入得: ,解得: ,
∴ ,
当x=10时,y=800万m3
(2)解:设 ,把(10,0),(50,880)代入得: ,解得: ,∴ ,当0≤x≤10时, ;当10<x≤50时, ,
∴
当y=840时
,解得:x=8,
,解得:x=30.由图象可得:8≤x≤30
【解析】【分析】(1)根据点(0,1000),(50,0)在直线l1上,设函数解析式,利用待定系数法求出其函数解析式即可。
(2)根据点(10,0),(50,880)在直线l2上,设函数解析式,利用待定系数法求出其函数解析式,再分别求出当0≤x≤10时和当10<x≤50时,y与x的函数解析式,然后在分别求出y=840时的自变量的值,即可写出发生严重干旱时x的范围。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
19.2.3一次函数与方程、不等式
一、填空题
1.如图:点在直线上,则不等式关于的解集是 .
2.若直线y=kx+3的图象经过点(2,0),则关于x的不等式kx+3>0的解集是 .
3.已知一次函数 与 图象如图所示,则下列结论:① ;② ;③关于 的方程 的解为 ;④当 , .其中正确的有 (填序号).
4.一次函数y=-2x+4与x轴的交点坐标是 。
二、单选题
5.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( )
A. B. C. D.
6.若函数 的图象如图所示,则关于 的不等式 的解集为( )
A. B. C. D.
7.如图,直线分别与轴、轴交于点和点,直线分别与轴、轴交于点和点,点是内部(包括边上)的一点,则的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
8.一次函数和与的部分对应值如表1,与的部分对应值如表2:
0 1 0 1
3 5 0 -1
则当时,的取值范围是( )
A. B. C. D.
三、解答题
9.在同一直角坐标系内分别作出一次函数y=5﹣x和y=2x﹣1的图象,这两个图象有交点吗?如果有请你结合图象直接写出交点的坐标?
四、综合题
10.如图,已知函数y=2x﹣5,观察图象回答下列问题
(1)x 时,y<0;
(2)y 时,x<3.
11.在平面直角坐标系中,直线 分别交x轴、y轴于点A、B将△AOB绕点O顺时针旋转90°后得到 .
(1)求直线 的解析式;
(2)若直线 与直线l相交于点C,求 的面积.
12.由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少.已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示.针对这种干旱情况,从第10天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
(1)求原有蓄水量y1(万m3)与干旱持续时间x(天)的函数关系式,并求x=10时的水库总蓄水量.
(2)求当0≤x≤50时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x 的范围),若总蓄水量不多于840万m3为严重干旱,直接写出发生严重干旱时x的范围.
答案解析部分
1.【答案】
【解析】【解答】
方法1:
点在直线上∴ y=3时,x=-2
由图分析可知,当,x≤-2
方法2:
∵ 点在直线上
∴ -2k+b=3
∴ b=3+2k
∴ kx+3+2k≥3
∴ kx+2k≥0
∴ k(x+2)≥0
∴ x+2≤0
即 x≤-2
【分析】本题考查一次函数与一元一次不等式的关系。 利用一次函数图象解一元一次不等式要先找线,由y的范围确定图象,对应的横坐标x的取值范围就是一元一次不等式的解集。或者点在函数上,得到b的代数式,再代入求不等式的解集也可。
2.【答案】
【解析】【解答】解:∵直线y=kx+3的图象经过点(2,0),
∴0=2k+3,
解得k=- ,
则不等式kx+3>0为- x+3>0,
解得:x<2,
故答案为:x<2.
【分析】把点(2,0)代入解析式,利用待定系数法求出k的值,然后再解不等式即可.
3.【答案】③④
【解析】【解答】解:∵一次函数y1=kx+b经过第一、二、四象限,
∴k<0,b>0,所以①错误;
∵直线y2=x+a的图象与y轴的交点在x轴下方,
∴a<0,所以②错误;
∵一次函数y1=kx+b与y2=x+a的图象的交点的横坐标为3,
∴x=3时,kx+b=x﹣a,所以③正确;
当x>3时,y1<y2,所以④正确.
故答案为 :③④.
【分析】根据一次函数的图象、系数与性质对①②进行判断;利用一次函数与一元一次方程的关系对③进行判断;利用函数图象,当x>3时,一次函数y1=kx+b在直线y2=x+a的下方,则可对④进行判断.
4.【答案】(2,0)
【解析】【解答】解:当y=0时-2x+4=0
解之:x=2
∴交点坐标为:(2,0).
故答案为:(2,0).
【分析】由y=0建立关于x的方程,解方程求出x的值,即可得到一次函数图象与x轴的交点坐标。
5.【答案】B
【解析】【解答】解:∵函数y=ax+b和y=kx的图象交于点P的坐标为(-4,-2),
∴关于x,y的二元一次方程组的解是.
故答案为:B.
【分析】结合函数图象,利用两函数图象的交点坐标即是二元一次方程组的解求解即可。
6.【答案】B
【解析】【解答】解:由函数图象可得一次函数y=kx+b经过点(3,0),
∴当x>3时,y=kx+b<0,
故答案为:B.
【分析】由图知,直线与x轴的交点式(3,0),而不等式kx+b<0即是直线在x轴的下方的部分,其对应的x的值在3的右边部分,所以可得不等式的解集为x>3。
7.【答案】B
【解析】【解答】 解:点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示,
当P为直线y=2与直线y2的交点时,m取最大值,
当P为直线y=2与直线y1的交点时,m取最小值,
∵y1=-x+3中令y=2,则x=1,
y2=x+3中令y=2,则x=-1,
∴m的最大值为1,m的最小值为-1.
则m的最大值与最小值之差为:1-(-1)=2
故选:B.
【分析】 根据一次函数的性质,因为P的纵坐标为2,故点P在直线y=2上,则P点位于两条边上即可得到最值,当P点位于y2上时m有最小值,当P点位于y1上时m有最大值,故可求得.
8.【答案】C
【解析】【解答】解:将(0,3)、(1,5)代入y1=k1x+b1中可得
解得,
∴y1=2x+3.
将(0,0)、(1,-1)代入y2=k2x+b2中可得
解得,
∴y2=-x.
联立y1=2x+3、y2=-x可得,
∴当y1>y2>0时,-1
【分析】利用待定系数法求出y1、y2,联立求出两一次函数图象的交点坐标,据此解答.
9.【答案】解:如图,
根据图象得到交点坐标为(2,3)
【解析】【分析】首先利用两点法作图作出两个函数的图象,即可得出交点坐标.
10.【答案】(1)<2.5
(2)<1
【解析】【解答】解:(1)当x<2.5时,y<0;
2)当x=3时,y=2x﹣5=1,
所以y<1时,x<3.
故答案为<2.5,<1.
【分析】(1)写出函数图象在x轴下方所对应的自变量的取值范围即可;(2)先计算出自变量为3所对应的函数值,然后利用图象和判断x<3时所对应的函数值的范围.
11.【答案】(1)解:由直线l: 分别交x轴,y轴于点A、B.可知:A(3,0),B(0,4).∵△AOB绕点O顺时针旋转90°而得到△A′OB′,∴△AOB≌△A′OB′,故A′(0,﹣3),B′(4,0).设直线A′B′的解析式为y=kx+b(k≠0,k,b为常数)
∴ ,解得: ,∴直线A′B′的解析式为
(2)解:由题意得: ,解得: ,∴C( ,﹣ ),又A′B=3+4=7,∴S△A′BC= =
【解析】【分析】(1)首先根据坐标轴上点的坐标特点,求出A,B两点的坐标,由于△AOB绕点O顺时针旋转90°而得到△A′OB′,根据旋转的性质△AOB≌△A′OB′,从而得出A′,B′的坐标,再用待定系数法,求出直线A′B′的解析式;
(2)解直线A′B′的解析式与直线l的解析式联立的方程组,得出C点的坐标,然后根据三角形的面积公式得出答案。
12.【答案】(1)解:设 ,把(0,1000),(50,0)代入得: ,解得: ,
∴ ,
当x=10时,y=800万m3
(2)解:设 ,把(10,0),(50,880)代入得: ,解得: ,∴ ,当0≤x≤10时, ;当10<x≤50时, ,
∴
当y=840时
,解得:x=8,
,解得:x=30.由图象可得:8≤x≤30
【解析】【分析】(1)根据点(0,1000),(50,0)在直线l1上,设函数解析式,利用待定系数法求出其函数解析式即可。
(2)根据点(10,0),(50,880)在直线l2上,设函数解析式,利用待定系数法求出其函数解析式,再分别求出当0≤x≤10时和当10<x≤50时,y与x的函数解析式,然后在分别求出y=840时的自变量的值,即可写出发生严重干旱时x的范围。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
