第十九章 一次函数综合复习题(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第十九章一次函数综合复习题
一、单选题
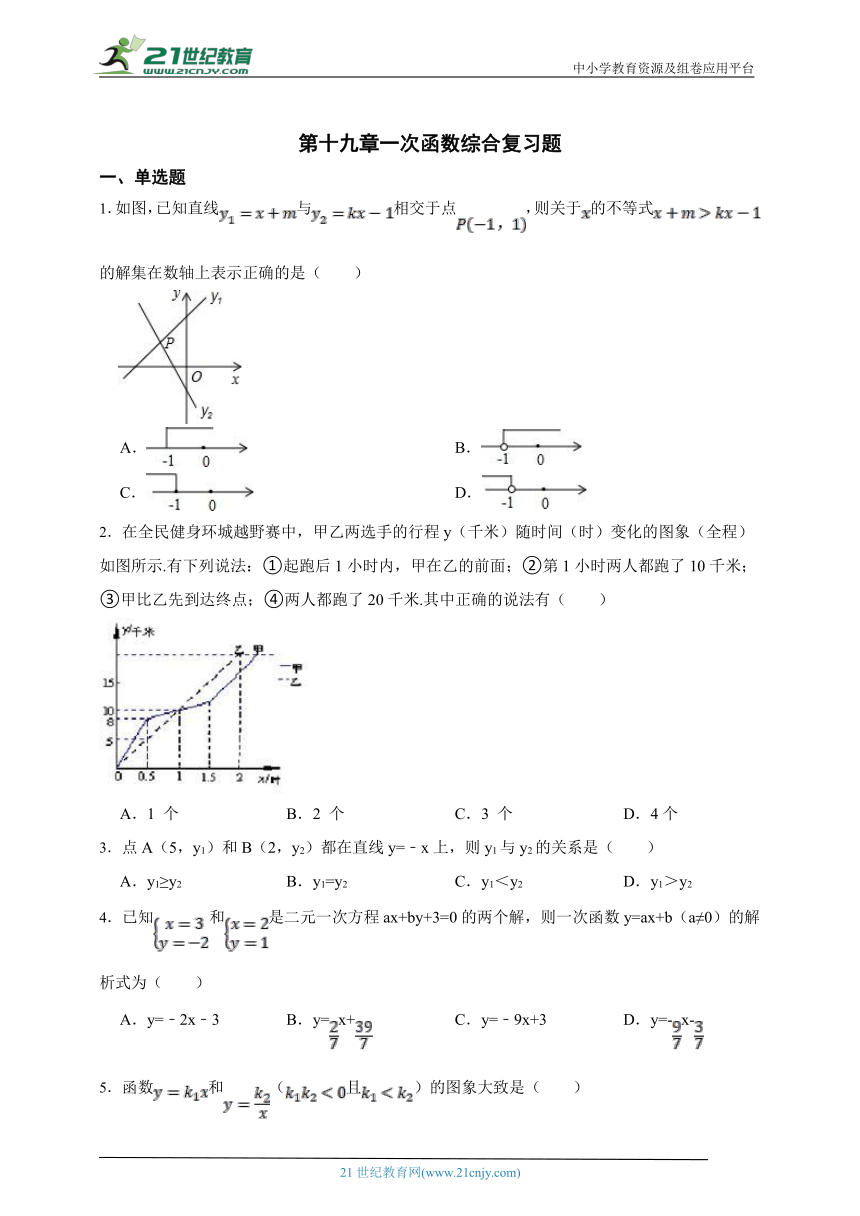
1.如图,已知直线与相交于点,则关于的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
2.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )
A.1 个 B.2 个 C.3 个 D.4个
3.点A(5,y1)和B(2,y2)都在直线y=﹣x上,则y1与y2的关系是( )
A.y1≥y2 B.y1=y2 C.y1<y2 D.y1>y2
4.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( )
A.y=﹣2x﹣3 B.y=x+ C.y=﹣9x+3 D.y=-x-
5.函数和(且)的图象大致是( )
A. B.
C. D.
6.下列函数中,自变量x的取值范围是x≥2的是( )
A. B. C. D.
7.已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是( )
A.-28.在平面直角坐标系中,已知点A(-2,3),B(2,1),若抛物线y=ax2-2x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
A. B.
C. D.a≤-1/2或a≥1
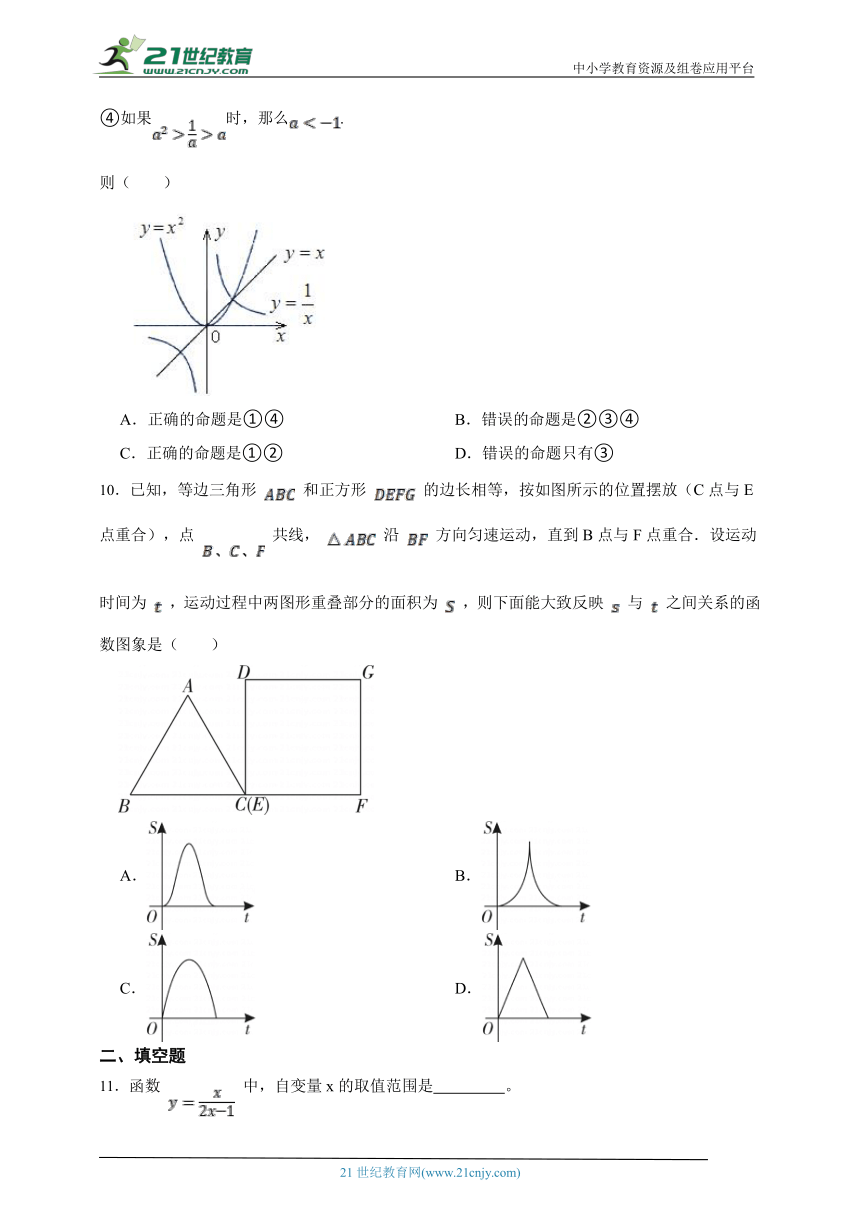
9.给出下列命题及函数,和的图象
①如果,那么;
②如果,那么;
③如果,那么;
④如果时,那么.
则( )
A.正确的命题是①④ B.错误的命题是②③④
C.正确的命题是①② D.错误的命题只有③
10.已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放(C点与E点重合),点 共线, 沿 方向匀速运动,直到B点与F点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是( )
A. B.
C. D.
二、填空题
11.函数 中,自变量x的取值范围是 。
12.在“变量之间的关系”一章中,我们学习的“变量”是指自变量和因变量,而表达它们之间关系的通常有三种方法,这三种方法是指 、 和
13.根据如图的程序计算,当输入时,输出的结果y= ;当输出的结果时,则输入x= .
14.如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 .
15.如图,正比例函数的图象过点.直线沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.当点A关于直线BC的对称点恰好落在y轴上时,则的面积是 .
三、计算题
16.求下列函数当x=-2时的函数值.
(1)y=x-3.
(2)y=
(3)y=.
17.已知是的一次函数,当时,;当时,,求
(1)这个一次函数的表达式
(2)当时,自变量的值。
(3)时,自变量的取值范围。
四、解答题
18.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值时,y是x的正比例函数.
19.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
20. 如图,在平面直角坐标系中,一次函数的图象向下平移得到一次函数,若平移后的函数图象经过点,
(1)求,的值;
(2)对于自变量的每一个值,一次函数,和,所对应的函数值分别记为,,,若当时,总有,请你直接写出n的取值范围.
五、综合题
21.如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线OAC运动.
(1)求直线BC的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点P的坐标.
22.已知如图,一次函数y=kx+b的图象与反比例函数 的图象相交于A、B两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
23.如图,正比例函数 的图象与反比例函数 在第一象限的图象交于 点,过 点作 轴的垂线,垂足为 ,△ 的面积为1.
(1)求反比例函数的表达式;
(2)如果 为反比例函数在第一象限图象上的点(点 与点 不重合),且 点的横坐标为1,在 轴上求一点 ,使 最小.
24.在平面直角坐标系中,A(a,b)、B(c,d)、C(7,0),且
(1)如果a=1,d=2,
①求A,B两点的坐标;
②求线段AB与y轴交点N的坐标,并求出△AOB的面积;
(2)如果b=-1,且△AOB与△ABC面积和为9,求a的值或取值范围.
答案解析部分
1.【答案】B
【解析】【解答】解:∵ 直线与相交于点 ,
观察图象知:当x>-1时,直线在图象的上方,
∴ 关于的不等式的解集为x>-1,
在数轴上表示为:
故答案为:B.
【分析】观察图象知当x>-1时,直线在图象的上方,据此求出解集再判断即可.
2.【答案】C
【解析】【分析】从图象上来看,甲乙的起跑点是一样的,在起跑一小时后,甲乙在同一点,在起跑后到1小时之间,甲的图形都比乙的图形高,说明起跑后1小时内,甲在乙的前面,所以①正确,通过图象观察,一小时时该点的纵坐标是10,所以第1小时两人都跑了10千米,所以②正确;观察图形,当时间为2小时时候,乙已经到达终点,而此时甲还没到达,所以甲比乙先到达终点是错误的,所以③错误;观察图形,当时间为2小时时候,乙已经到达终点,此时纵坐标为20,所以两人都跑了20千米,所以④正确,综上所述,①②④正确,所以选C
【点评】本题考查函数图象,解答本题需要考生会观察函数图象,得出有用的信息,从而来判断正确还是错误
3.【答案】C
【解析】【解答】解:∵点A(5,y1)和B(2,y2)都在直线y=﹣x上,
∴y1=﹣5,y2=﹣2,
∵﹣5<﹣2,
∴y1<y2.
故选:C.
【分析】分别把点A(5,y1)和B(2,y2)代入直线y=﹣x,求出y1,y2的值,再比较出其大小即可.
4.【答案】D
【解析】【解答】解:∵和是二元一次方程ax+by+3=0的两个解,
∴,
解得:,
∴一次函数y=ax+b(a≠0)的解析式为y=-x-
故选:D.
【分析】由已知方程的解,可以把这对数值代入方程,得到两个含有未知数a,b的二元一次方程,联立方程组求解,从而可以求出a,b的值,进一步得出解析式即可.
5.【答案】B
【解析】【解答】由条件 可知, ,
当 时 的图像经过第二、四象限,
当 时 的图像经过第一、三象限,
故答案为:B.
【分析】根据一次函数与反比例函数的图象与系数的关系逐项判断即可。
6.【答案】B
【解析】【解答】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,得函数,,,自变量x的取值范围分别为x≤2, x≥2, -2≤x≤2, x>2.
故选B.
【分析】二次根式有意义的条件是:被开方数为非负数;分式有意义的条件是:分母不为0.根据上述条件得到自变量x的取值范围x≥2的函数即可.
7.【答案】B
【解析】【解答】解 :由题意得 :
0<2m-1<m+2 ① ;0<2m-1<-2m+4② ;
解得 :;
故应选 B.
【分析】此题分两种情况①点P在x轴上方在直线l1右边;列出不等式0<2m-1<m+2,②点P在x轴上方在直线l2左边,列出不等式0<2m-1<-2m+4,解两不等式组成的不等式组,即可得出答案。
8.【答案】A
【解析】【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵A(-2,3),B(2,1),
∴,解得 ,
∴直线AB的解析式为y= x+2,
∴联立,得y= x+2=ax2-2x+1,整理得ax2- x-1=0,
∵抛物线与线段AB有两个不同的交点,
∴=b2-4ac>0,即( )2+4a>0,解得a> ,
①当a>0,抛物线经过点B(2,1)时,
则y=a-2a+1≥1,即当a≥1时,抛物线与线段AB有两个不同交点,
②当a<0,抛物线经过点B(-2,3)时,
则y=4a+4+1≤3,即当a≤ 时,抛物线与线段AB有两个不同交点,
∴综上所述,a的取值范围为a≥1或 <a≤ .
故答案为:A.
【分析】用待定系数法先求出直线AB的解析式,再与抛物线解析式联立方程组,由抛物线与线段AB有两个不同的交点,先根据 =b2-4ac>0求得a> ,再讨论a>0和a<0两种情况下,求出a的取值范围,即可解决问题.
9.【答案】A
【解析】【分析】根据二次函数、反比例函数、正比例函数的图象的上下关系即可得出结论:
①当三个函数的图象依,,次序呈上下关系时, ,命题正确;
②当三个函数的图象依,,次序呈上下关系时,或 ,命题错误;
③当三个函数的图象没有出现,,次序的上下关系 ,命题错误;
④当三个函数的图象依,,次序呈上下关系时, ,命题正确.
综上所述,正确的命题是①④.故选A.
10.【答案】A
【解析】【解答】解:设等边三角形ABC和正方形DEFG的边长都为a,运动速度为1,
当点C在EF的中点左侧时,
设AC交DE于点H,
则CE=t,HE=ECtan∠ACB=t× = t,
则S=S△CEH= ×CE×HE= ×t× t= ,
可知图象为开口向上的二次函数,
当点C在EF的中点右侧时,设AB与DE 交于点M,
则EC=t,BE=a-t,ME= ,
∴S= ,
可知图象为开口向下的二次函数;
当点C在F点右侧且B在EF中点的左侧时,
S= ,
可知图象为开口向下的二次函数;
当点C在F点右侧且B在EF中点的右侧时,
此时BF=2a-t,MF= ,
∴ ,
可知图象为开口向上的二次函数;
故答案为:A
【分析】分点C在EF中点的左侧、点C在EF中点的右侧、点C在F点右侧且B在EF中点的左侧,点C在F点右侧且B在EF中点的右侧四种情况,分别求出函数的表达式即可求解.
11.【答案】
【解析】【解答】根据题意得:2x-1≠0, .
故答案为: .
【分析】根据分式的意义,分母不等于0,可以求出x的范围。
12.【答案】表格法;解析式法;图象法
【解析】【解答】解:表示两个变量之间的关系时,通常有三种方法:
表格法,解析式法,图象法.
故答案为:表格法,解析式法,图象法.
【分析】根据常用的函数表示方法:表格法,解析式法,图象法进行填写.
13.【答案】2;0.7
【解析】【解答】解:因为,
所以;
当输出的结果时,分以下两种情况:
①当时,则,解得,不符合题设,舍去,
②当时,则,解得,符合题设,
所以输入,
故答案为:2,0.7.
【分析】根据程序计算可知:当x=3>1时,代入y=-x+5求值;当y=5.7时,可得y=-x+5=5.7或y=x+5=5.7,分别求出x值再检验即可.
14.【答案】5
【解析】【解答】解:∵点P 在“勾股一次函数”y= 的图象上,
∴ 即 ,
又∵a,b,c分别是Rt△ABC的三条变长,∠C=90°,Rt△ABC的面积是5,
∴ ,即ab=10,
又∵a2+b2=c2,
∴(a+b)2﹣2ab=c2,
即∴
解得c=5,
故答案为:5.
【分析】把点P 的坐标代入y= ,可得a、b、c的关系 ,根据面积是5可得ab=10,最后利用完全平方公式(a+b)2﹣2ab=c2得到关于c的方程,求解即可。
15.【答案】
【解析】【解答】解:将点A(2, 4)代入y=kx中,得 4=2k,即k= 2,
∴直线OA的解析式为y= 2x,
在y=x+b中,令y=0,则x= b,
∴B( b,0),即OB=|b|,
在y=x+b中,令x=0,则y=b,
∴C(0,b),即OC=|b|,
∴OB=OC,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
∵点A关于直线BC的对称点A′恰好落在y轴上,
∴CD垂直平分AA′,
∴CA=CA′,
∴∠ACD=∠OCB=45°,
∴∠ACO=90°,
∴OC=|yA|=4,
∴OB=OC=4,即C(0, 4),
将点C(0, 4)代入y=x+b中,得 4=0+b,
∴b= 4,
∴直线BC的解析式为y=x 4,
由 ,得,
∴点D(, ),
∴S△OBD=OB =.
故答案为:.
【分析】将A(2,-4)代入y=kx中得k的值,得直线OA的解析式,易得B(-b,0),C(0,b),OB=OC=|b|,∠OCB=∠OBC=45°,由题意可得CD垂直平分AA′,则CA=CA′,根据等腰三角形的性质得∠ACD=∠OCB=45°,则∠ACO=90°,OC=|yA|=4,C(0,-4),代入y=x+b中可得b的值,求出直线BC的解析式,联立直线OA的解析式求出x、y,可得点D的坐标,然后根据三角形的面积公式进行计算.
16.【答案】(1)解:当x=-2时y=×(-2)-3=-1-3=-4.
(2)解:当x=-2时,
(3)解:当x=-2时
.
【解析】【分析】(1)将x=-2代入函数解析式,可求出对应的y的值.
(2)将x=-2代入函数解析式,可求出对应的y的值.
(3)将x=-2代入函数解析式,进行计算,可求出y的值.
17.【答案】(1)解:设一次函数的解析式为y=kx+b,
点(3,1)和(-2,-14)在函数上,
将其代入解析式,可得,
解得,
所以一次函数的解析式为y=3x-8;
(2)解:当y=-7时,
-7=3x-8,
解得x=;
(3)解: 当时 ,
即-13x-8<1,
解得.
【解析】【分析】(1)根据待定系数法求解一次函数的解析式;
(2)根据一次函数的性质,已知y的值,代入函数解析式就可以求出x的值;
(3)根据不等式的性质,先移项,再将x前的系数变为1,即可求出x的取值范围.
18.【答案】解答: 由函数是一次函数可得,m+1≠0,解得 m≠-1,所以,m≠-1时,y是x的一次函数;函数为正比例函数时,m+1≠0且m2-1=0,解得 m=1,所以,当m=1时,y是x的正比例函数
【解析】【分析】根据一次函数和正比例函数的定义解题,特别注意:当函数为正比例函数时m+1≠0且m2-1=0
19.【答案】解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为6千克时(在允许范围内)时的弹簧长度=18+2×6=30厘米.
【解析】【分析】(1)因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
(2)由表可知,当物体的质量为3kg时,弹簧的长度是24cm;不挂重物时,弹簧的长度是18cm;
(3)由表中的数据可知,x=0时,y=18,并且每增加1千克的质量,长度增加2cm,依此可求所挂重物为6千克时(在允许范围内)时的弹簧长度.
20.【答案】(1)解:一次函数的图象向下平移得到一次函数,
,
一次函数的解析式为,
平移后的函数图象经过点,
,
;
(2)当或时,在的范围内,恒成立.
【解析】【解答】解:(2)函数与中,随的增大而增大,
在的范围内,,,
当时,函数中随的增大而增大,
在的范围内,,
在的范围内,恒成立,
,
解得:,
;
当时,函数中随的增大而减小,
在的范围内,,
在的范围内,恒成立,
,
解得:,
此时;
综上所述:当或时,在的范围内,恒成立.
【分析】(1)根据题意先求出 一次函数的解析式为, 再计算求解即可;
(2)根据题意先求出在的范围内,,,再分类讨论,列不等式组计算求解即可。
21.【答案】(1)解:设直线BC的解析式是,根据题意得:
解得
则直线的解析式是:;
(2)解:在中,令,解得:
则;
(3)解:设的解析式是,则,
解得:,
则直线的解析式是:,
∵当的面积是的面积的时,∴P的横坐标是,
在中,当时,,则P的坐标是;
在中,则,则P的坐标是
∴的坐标是:.
【解析】【分析】(1)利用待定系数法求出直线BC的解析式即可;
(2)先求出点A的横坐标,再利用三角形的面积公式求出的面积;
(3)先求出直线OA的解析式,求出点P的横坐标,再将点P的横坐标分别代入和求出点P的坐标即可。
22.【答案】(1)解:据题意,反比例函数 的图象经过点A(﹣2,1),
∴有m=xy=﹣2
∴反比例函数解析式为y=﹣ ,
又反比例函数的图象经过点B(1,n)
∴n=﹣2,
∴B(1,﹣2)
将A、B两点代入y=kx+b,有 ,
解得 ,
∴一次函数的解析式为y=﹣x﹣1
(2)解:一次函数的值大于反比例函数的值时,
x取相同值,一次函数图象在反比例函数上方即一次函数大于反比例函数,
∴x<﹣2或0<x<1
【解析】【分析】(1)利用待定系数法,分别得出反比例函数解析式和一次函数解析式。
(2)根据一次函数与反比例函数的图象,直接写出x的取值范围。
23.【答案】(1)解:设A点的坐标为( , ),
则 .∴ .
∵ ,∴ .∴ .
∴ 反比例函数的表达式为 .
(2)解:由 得 ∴ A为 .
设A点关于 轴的对称点为C,则C点的坐标为 .
如要在 轴上求一点P,使PA+PB最小,即 最小,则P点应为BC和x轴的交点,如图.
令直线BC的表达式为 .
∵ B为( , ),∴∴
∴ BC的表达式为 .
当 时, .∴ P点坐标为
【解析】【分析】(1) 设A点的坐标为( , ),则AM=b,OM=a, 根据反比例函数图象上的点的坐标特点得出 ,即①, 根据三角形的面积计算方法得出②,将①代入②,求解即可得出k的值,从而求出反比函数的解析式;
(2)解联立正比例函数与反比例函数的解析式组成的方程组,求解得出A点的坐标, 设A点关于 轴的对称点为C ,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数得出C点的坐标, 如要在 轴上求一点P,使PA+PB最小,即 最小,则P点应为BC和x轴的交点,如图. 利用待定系数法求出直线BC的解析式,再根据直线BC与x轴交点的坐标特点即可求出P点的坐标。
24.【答案】(1)解:由题意知:a-c-4=0,b-d-2=0,
∵a=1,d=2,
∴c=1-4=-3,b=2+2=4,
①易得A(1,4),B(-3,2);
②设直线AB的解析式为y=kx+n,
由题意得 ,
解得 ,
∴直线AB的解析式为 ,
令x=0,
则 ,
∴N(0, ),
;
(2)解:如果b=-1,
则d=-1-2=-3,
∵c=a-4,
∴ ,
同②可求得此时直线AB的解析式为 ,
当O、C两点在直线的两侧时,
如图所示,
则 ,
∴ ,
可以看到这种情况下不满足题意;
当O、C两点都在直线的左侧时,
如图,作BD⊥x轴于D,连接DA,
则 ,
结合A、B两点的坐标可以求到 ,
∵ ,
, ,
此时,若△AOB与△ABC面积和为9,
则 ,
解得 ;
当O、C两点都在直线的右侧时,
如图,延长BA于x轴交于点E,
由 可知,
当y=0时,
求得 ,
,
,
,
此时,若△AOB与△ABC面积和为9,
则 ,
解得 ,
综上所述, 或 .
【解析】【分析】(1)①根据非负数的性质得到a-c-4=0,b-d-2=0,根据a=1,d=2即可求出a和b的值,得到A和B的坐标;②求出直线AB的解析式,令x=0,求到y值,即可得到点N的坐标;(2)当b=-1时,可以求到d=-3,由(1)知c=a-4,即可得出A和B的坐标,算出直线AB的解析式,之后画图来计算△AOB与△ABC的面积,去讨论其和等于9的情况,发现O和C在直线同一侧的时候,面积是变化的值,不同侧的时候,面积是定值等于7,所以将同侧分别画图计算即可得到答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第十九章一次函数综合复习题
一、单选题
1.如图,已知直线与相交于点,则关于的不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
2.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法有( )
A.1 个 B.2 个 C.3 个 D.4个
3.点A(5,y1)和B(2,y2)都在直线y=﹣x上,则y1与y2的关系是( )
A.y1≥y2 B.y1=y2 C.y1<y2 D.y1>y2
4.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( )
A.y=﹣2x﹣3 B.y=x+ C.y=﹣9x+3 D.y=-x-
5.函数和(且)的图象大致是( )
A. B.
C. D.
6.下列函数中,自变量x的取值范围是x≥2的是( )
A. B. C. D.
7.已知平面内有两条直线l1:y=x+2,l2:y=-2x+4交于点A,与x轴分别交于B,C两点,P(m,2m-1)落在△ABC内部(不含边界),则m的取值范围是( )
A.-2
A. B.
C. D.a≤-1/2或a≥1
9.给出下列命题及函数,和的图象
①如果,那么;
②如果,那么;
③如果,那么;
④如果时,那么.
则( )
A.正确的命题是①④ B.错误的命题是②③④
C.正确的命题是①② D.错误的命题只有③
10.已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放(C点与E点重合),点 共线, 沿 方向匀速运动,直到B点与F点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是( )
A. B.
C. D.
二、填空题
11.函数 中,自变量x的取值范围是 。
12.在“变量之间的关系”一章中,我们学习的“变量”是指自变量和因变量,而表达它们之间关系的通常有三种方法,这三种方法是指 、 和
13.根据如图的程序计算,当输入时,输出的结果y= ;当输出的结果时,则输入x= .
14.如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 .
15.如图,正比例函数的图象过点.直线沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.当点A关于直线BC的对称点恰好落在y轴上时,则的面积是 .
三、计算题
16.求下列函数当x=-2时的函数值.
(1)y=x-3.
(2)y=
(3)y=.
17.已知是的一次函数,当时,;当时,,求
(1)这个一次函数的表达式
(2)当时,自变量的值。
(3)时,自变量的取值范围。
四、解答题
18.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值时,y是x的正比例函数.
19.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
20. 如图,在平面直角坐标系中,一次函数的图象向下平移得到一次函数,若平移后的函数图象经过点,
(1)求,的值;
(2)对于自变量的每一个值,一次函数,和,所对应的函数值分别记为,,,若当时,总有,请你直接写出n的取值范围.
五、综合题
21.如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线OAC运动.
(1)求直线BC的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点P的坐标.
22.已知如图,一次函数y=kx+b的图象与反比例函数 的图象相交于A、B两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
23.如图,正比例函数 的图象与反比例函数 在第一象限的图象交于 点,过 点作 轴的垂线,垂足为 ,△ 的面积为1.
(1)求反比例函数的表达式;
(2)如果 为反比例函数在第一象限图象上的点(点 与点 不重合),且 点的横坐标为1,在 轴上求一点 ,使 最小.
24.在平面直角坐标系中,A(a,b)、B(c,d)、C(7,0),且
(1)如果a=1,d=2,
①求A,B两点的坐标;
②求线段AB与y轴交点N的坐标,并求出△AOB的面积;
(2)如果b=-1,且△AOB与△ABC面积和为9,求a的值或取值范围.
答案解析部分
1.【答案】B
【解析】【解答】解:∵ 直线与相交于点 ,
观察图象知:当x>-1时,直线在图象的上方,
∴ 关于的不等式的解集为x>-1,
在数轴上表示为:
故答案为:B.
【分析】观察图象知当x>-1时,直线在图象的上方,据此求出解集再判断即可.
2.【答案】C
【解析】【分析】从图象上来看,甲乙的起跑点是一样的,在起跑一小时后,甲乙在同一点,在起跑后到1小时之间,甲的图形都比乙的图形高,说明起跑后1小时内,甲在乙的前面,所以①正确,通过图象观察,一小时时该点的纵坐标是10,所以第1小时两人都跑了10千米,所以②正确;观察图形,当时间为2小时时候,乙已经到达终点,而此时甲还没到达,所以甲比乙先到达终点是错误的,所以③错误;观察图形,当时间为2小时时候,乙已经到达终点,此时纵坐标为20,所以两人都跑了20千米,所以④正确,综上所述,①②④正确,所以选C
【点评】本题考查函数图象,解答本题需要考生会观察函数图象,得出有用的信息,从而来判断正确还是错误
3.【答案】C
【解析】【解答】解:∵点A(5,y1)和B(2,y2)都在直线y=﹣x上,
∴y1=﹣5,y2=﹣2,
∵﹣5<﹣2,
∴y1<y2.
故选:C.
【分析】分别把点A(5,y1)和B(2,y2)代入直线y=﹣x,求出y1,y2的值,再比较出其大小即可.
4.【答案】D
【解析】【解答】解:∵和是二元一次方程ax+by+3=0的两个解,
∴,
解得:,
∴一次函数y=ax+b(a≠0)的解析式为y=-x-
故选:D.
【分析】由已知方程的解,可以把这对数值代入方程,得到两个含有未知数a,b的二元一次方程,联立方程组求解,从而可以求出a,b的值,进一步得出解析式即可.
5.【答案】B
【解析】【解答】由条件 可知, ,
当 时 的图像经过第二、四象限,
当 时 的图像经过第一、三象限,
故答案为:B.
【分析】根据一次函数与反比例函数的图象与系数的关系逐项判断即可。
6.【答案】B
【解析】【解答】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,得函数,,,自变量x的取值范围分别为x≤2, x≥2, -2≤x≤2, x>2.
故选B.
【分析】二次根式有意义的条件是:被开方数为非负数;分式有意义的条件是:分母不为0.根据上述条件得到自变量x的取值范围x≥2的函数即可.
7.【答案】B
【解析】【解答】解 :由题意得 :
0<2m-1<m+2 ① ;0<2m-1<-2m+4② ;
解得 :;
故应选 B.
【分析】此题分两种情况①点P在x轴上方在直线l1右边;列出不等式0<2m-1<m+2,②点P在x轴上方在直线l2左边,列出不等式0<2m-1<-2m+4,解两不等式组成的不等式组,即可得出答案。
8.【答案】A
【解析】【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵A(-2,3),B(2,1),
∴,解得 ,
∴直线AB的解析式为y= x+2,
∴联立,得y= x+2=ax2-2x+1,整理得ax2- x-1=0,
∵抛物线与线段AB有两个不同的交点,
∴=b2-4ac>0,即( )2+4a>0,解得a> ,
①当a>0,抛物线经过点B(2,1)时,
则y=a-2a+1≥1,即当a≥1时,抛物线与线段AB有两个不同交点,
②当a<0,抛物线经过点B(-2,3)时,
则y=4a+4+1≤3,即当a≤ 时,抛物线与线段AB有两个不同交点,
∴综上所述,a的取值范围为a≥1或 <a≤ .
故答案为:A.
【分析】用待定系数法先求出直线AB的解析式,再与抛物线解析式联立方程组,由抛物线与线段AB有两个不同的交点,先根据 =b2-4ac>0求得a> ,再讨论a>0和a<0两种情况下,求出a的取值范围,即可解决问题.
9.【答案】A
【解析】【分析】根据二次函数、反比例函数、正比例函数的图象的上下关系即可得出结论:
①当三个函数的图象依,,次序呈上下关系时, ,命题正确;
②当三个函数的图象依,,次序呈上下关系时,或 ,命题错误;
③当三个函数的图象没有出现,,次序的上下关系 ,命题错误;
④当三个函数的图象依,,次序呈上下关系时, ,命题正确.
综上所述,正确的命题是①④.故选A.
10.【答案】A
【解析】【解答】解:设等边三角形ABC和正方形DEFG的边长都为a,运动速度为1,
当点C在EF的中点左侧时,
设AC交DE于点H,
则CE=t,HE=ECtan∠ACB=t× = t,
则S=S△CEH= ×CE×HE= ×t× t= ,
可知图象为开口向上的二次函数,
当点C在EF的中点右侧时,设AB与DE 交于点M,
则EC=t,BE=a-t,ME= ,
∴S= ,
可知图象为开口向下的二次函数;
当点C在F点右侧且B在EF中点的左侧时,
S= ,
可知图象为开口向下的二次函数;
当点C在F点右侧且B在EF中点的右侧时,
此时BF=2a-t,MF= ,
∴ ,
可知图象为开口向上的二次函数;
故答案为:A
【分析】分点C在EF中点的左侧、点C在EF中点的右侧、点C在F点右侧且B在EF中点的左侧,点C在F点右侧且B在EF中点的右侧四种情况,分别求出函数的表达式即可求解.
11.【答案】
【解析】【解答】根据题意得:2x-1≠0, .
故答案为: .
【分析】根据分式的意义,分母不等于0,可以求出x的范围。
12.【答案】表格法;解析式法;图象法
【解析】【解答】解:表示两个变量之间的关系时,通常有三种方法:
表格法,解析式法,图象法.
故答案为:表格法,解析式法,图象法.
【分析】根据常用的函数表示方法:表格法,解析式法,图象法进行填写.
13.【答案】2;0.7
【解析】【解答】解:因为,
所以;
当输出的结果时,分以下两种情况:
①当时,则,解得,不符合题设,舍去,
②当时,则,解得,符合题设,
所以输入,
故答案为:2,0.7.
【分析】根据程序计算可知:当x=3>1时,代入y=-x+5求值;当y=5.7时,可得y=-x+5=5.7或y=x+5=5.7,分别求出x值再检验即可.
14.【答案】5
【解析】【解答】解:∵点P 在“勾股一次函数”y= 的图象上,
∴ 即 ,
又∵a,b,c分别是Rt△ABC的三条变长,∠C=90°,Rt△ABC的面积是5,
∴ ,即ab=10,
又∵a2+b2=c2,
∴(a+b)2﹣2ab=c2,
即∴
解得c=5,
故答案为:5.
【分析】把点P 的坐标代入y= ,可得a、b、c的关系 ,根据面积是5可得ab=10,最后利用完全平方公式(a+b)2﹣2ab=c2得到关于c的方程,求解即可。
15.【答案】
【解析】【解答】解:将点A(2, 4)代入y=kx中,得 4=2k,即k= 2,
∴直线OA的解析式为y= 2x,
在y=x+b中,令y=0,则x= b,
∴B( b,0),即OB=|b|,
在y=x+b中,令x=0,则y=b,
∴C(0,b),即OC=|b|,
∴OB=OC,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
∵点A关于直线BC的对称点A′恰好落在y轴上,
∴CD垂直平分AA′,
∴CA=CA′,
∴∠ACD=∠OCB=45°,
∴∠ACO=90°,
∴OC=|yA|=4,
∴OB=OC=4,即C(0, 4),
将点C(0, 4)代入y=x+b中,得 4=0+b,
∴b= 4,
∴直线BC的解析式为y=x 4,
由 ,得,
∴点D(, ),
∴S△OBD=OB =.
故答案为:.
【分析】将A(2,-4)代入y=kx中得k的值,得直线OA的解析式,易得B(-b,0),C(0,b),OB=OC=|b|,∠OCB=∠OBC=45°,由题意可得CD垂直平分AA′,则CA=CA′,根据等腰三角形的性质得∠ACD=∠OCB=45°,则∠ACO=90°,OC=|yA|=4,C(0,-4),代入y=x+b中可得b的值,求出直线BC的解析式,联立直线OA的解析式求出x、y,可得点D的坐标,然后根据三角形的面积公式进行计算.
16.【答案】(1)解:当x=-2时y=×(-2)-3=-1-3=-4.
(2)解:当x=-2时,
(3)解:当x=-2时
.
【解析】【分析】(1)将x=-2代入函数解析式,可求出对应的y的值.
(2)将x=-2代入函数解析式,可求出对应的y的值.
(3)将x=-2代入函数解析式,进行计算,可求出y的值.
17.【答案】(1)解:设一次函数的解析式为y=kx+b,
点(3,1)和(-2,-14)在函数上,
将其代入解析式,可得,
解得,
所以一次函数的解析式为y=3x-8;
(2)解:当y=-7时,
-7=3x-8,
解得x=;
(3)解: 当时 ,
即-13x-8<1,
解得.
【解析】【分析】(1)根据待定系数法求解一次函数的解析式;
(2)根据一次函数的性质,已知y的值,代入函数解析式就可以求出x的值;
(3)根据不等式的性质,先移项,再将x前的系数变为1,即可求出x的取值范围.
18.【答案】解答: 由函数是一次函数可得,m+1≠0,解得 m≠-1,所以,m≠-1时,y是x的一次函数;函数为正比例函数时,m+1≠0且m2-1=0,解得 m=1,所以,当m=1时,y是x的正比例函数
【解析】【分析】根据一次函数和正比例函数的定义解题,特别注意:当函数为正比例函数时m+1≠0且m2-1=0
19.【答案】解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为6千克时(在允许范围内)时的弹簧长度=18+2×6=30厘米.
【解析】【分析】(1)因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
(2)由表可知,当物体的质量为3kg时,弹簧的长度是24cm;不挂重物时,弹簧的长度是18cm;
(3)由表中的数据可知,x=0时,y=18,并且每增加1千克的质量,长度增加2cm,依此可求所挂重物为6千克时(在允许范围内)时的弹簧长度.
20.【答案】(1)解:一次函数的图象向下平移得到一次函数,
,
一次函数的解析式为,
平移后的函数图象经过点,
,
;
(2)当或时,在的范围内,恒成立.
【解析】【解答】解:(2)函数与中,随的增大而增大,
在的范围内,,,
当时,函数中随的增大而增大,
在的范围内,,
在的范围内,恒成立,
,
解得:,
;
当时,函数中随的增大而减小,
在的范围内,,
在的范围内,恒成立,
,
解得:,
此时;
综上所述:当或时,在的范围内,恒成立.
【分析】(1)根据题意先求出 一次函数的解析式为, 再计算求解即可;
(2)根据题意先求出在的范围内,,,再分类讨论,列不等式组计算求解即可。
21.【答案】(1)解:设直线BC的解析式是,根据题意得:
解得
则直线的解析式是:;
(2)解:在中,令,解得:
则;
(3)解:设的解析式是,则,
解得:,
则直线的解析式是:,
∵当的面积是的面积的时,∴P的横坐标是,
在中,当时,,则P的坐标是;
在中,则,则P的坐标是
∴的坐标是:.
【解析】【分析】(1)利用待定系数法求出直线BC的解析式即可;
(2)先求出点A的横坐标,再利用三角形的面积公式求出的面积;
(3)先求出直线OA的解析式,求出点P的横坐标,再将点P的横坐标分别代入和求出点P的坐标即可。
22.【答案】(1)解:据题意,反比例函数 的图象经过点A(﹣2,1),
∴有m=xy=﹣2
∴反比例函数解析式为y=﹣ ,
又反比例函数的图象经过点B(1,n)
∴n=﹣2,
∴B(1,﹣2)
将A、B两点代入y=kx+b,有 ,
解得 ,
∴一次函数的解析式为y=﹣x﹣1
(2)解:一次函数的值大于反比例函数的值时,
x取相同值,一次函数图象在反比例函数上方即一次函数大于反比例函数,
∴x<﹣2或0<x<1
【解析】【分析】(1)利用待定系数法,分别得出反比例函数解析式和一次函数解析式。
(2)根据一次函数与反比例函数的图象,直接写出x的取值范围。
23.【答案】(1)解:设A点的坐标为( , ),
则 .∴ .
∵ ,∴ .∴ .
∴ 反比例函数的表达式为 .
(2)解:由 得 ∴ A为 .
设A点关于 轴的对称点为C,则C点的坐标为 .
如要在 轴上求一点P,使PA+PB最小,即 最小,则P点应为BC和x轴的交点,如图.
令直线BC的表达式为 .
∵ B为( , ),∴∴
∴ BC的表达式为 .
当 时, .∴ P点坐标为
【解析】【分析】(1) 设A点的坐标为( , ),则AM=b,OM=a, 根据反比例函数图象上的点的坐标特点得出 ,即①, 根据三角形的面积计算方法得出②,将①代入②,求解即可得出k的值,从而求出反比函数的解析式;
(2)解联立正比例函数与反比例函数的解析式组成的方程组,求解得出A点的坐标, 设A点关于 轴的对称点为C ,根据关于x轴对称的点的横坐标相同,纵坐标互为相反数得出C点的坐标, 如要在 轴上求一点P,使PA+PB最小,即 最小,则P点应为BC和x轴的交点,如图. 利用待定系数法求出直线BC的解析式,再根据直线BC与x轴交点的坐标特点即可求出P点的坐标。
24.【答案】(1)解:由题意知:a-c-4=0,b-d-2=0,
∵a=1,d=2,
∴c=1-4=-3,b=2+2=4,
①易得A(1,4),B(-3,2);
②设直线AB的解析式为y=kx+n,
由题意得 ,
解得 ,
∴直线AB的解析式为 ,
令x=0,
则 ,
∴N(0, ),
;
(2)解:如果b=-1,
则d=-1-2=-3,
∵c=a-4,
∴ ,
同②可求得此时直线AB的解析式为 ,
当O、C两点在直线的两侧时,
如图所示,
则 ,
∴ ,
可以看到这种情况下不满足题意;
当O、C两点都在直线的左侧时,
如图,作BD⊥x轴于D,连接DA,
则 ,
结合A、B两点的坐标可以求到 ,
∵ ,
, ,
此时,若△AOB与△ABC面积和为9,
则 ,
解得 ;
当O、C两点都在直线的右侧时,
如图,延长BA于x轴交于点E,
由 可知,
当y=0时,
求得 ,
,
,
,
此时,若△AOB与△ABC面积和为9,
则 ,
解得 ,
综上所述, 或 .
【解析】【分析】(1)①根据非负数的性质得到a-c-4=0,b-d-2=0,根据a=1,d=2即可求出a和b的值,得到A和B的坐标;②求出直线AB的解析式,令x=0,求到y值,即可得到点N的坐标;(2)当b=-1时,可以求到d=-3,由(1)知c=a-4,即可得出A和B的坐标,算出直线AB的解析式,之后画图来计算△AOB与△ABC的面积,去讨论其和等于9的情况,发现O和C在直线同一侧的时候,面积是变化的值,不同侧的时候,面积是定值等于7,所以将同侧分别画图计算即可得到答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
