四年级下册数学北师大版第三单元 小数乘法 整理与复习课件(共44张PPT)
文档属性
| 名称 | 四年级下册数学北师大版第三单元 小数乘法 整理与复习课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
北师版四年级数学下册
小数乘法
复习与整理
汇报人:XXX 时间:XXXXX
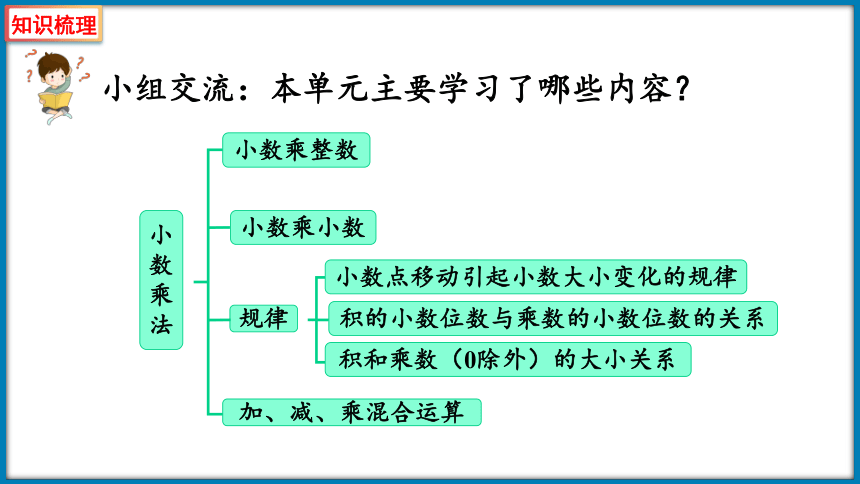
小组交流:本单元主要学习了哪些内容?
小数乘法
小数乘整数
小数乘小数
加、减、乘混合运算
规律
小数点移动引起小数大小变化的规律
积的小数位数与乘数的小数位数的关系
积和乘数(0除外)的大小关系
知识梳理
1. 小数乘整数的意义和整数乘法的意义相同,都是
求几个相同加数的和的简便运算;也可以说是求
这个小数的整数倍是多少。
2. 计算简单的小数乘整数,可以根据乘法的意义用
连加来计算;也可以转化成整数乘法来计算;也
可以借助直观示意图来计算。
1.小数乘整数
知识回顾
(1) 0.9×3=( 0.9 )+( 0.9 )+( 0.9 )(填相同的数)
解析:0.9×3可以表示3个0.9相加,即0.9+0.9+0.9。
(2) 0.8×4表示( 4个0.8相加是多少(或0.8的4倍是多 ),结果是( 3.2 )。
0.9
0.9
0.9
4个0.8相加是多少(或0.8的4倍是多少)
3.2
小数乘法的计算方法:先按照整数乘法的计算方法算出积,再看乘数中一共有几位小数,就从积的右边起数出几位,点上小数点。
积的位数不够时,先在积的左边添0补位,再点上小数点。
知识回顾
2.小数乘小数
(1) 根据19×16=304,在括号里填上适当的数。
①19×( 0.16 )=3.04
②( 0.19 )×1.6=0.304
③0.19×160=( 30.4 )
0.16
0.19
30.4
解析:①积是两位小数,两个乘数中一共应有两位小数,则括号中
的数是两位小数,是0.16;②积是三位小数,两个乘数中一共应有
三位小数,而乘数“1.6”是一位小数,则括号中的数应是两位小
数,是0.19;③19缩小到原来的是0.19,16扩大到原来的10倍是
160,则0.19×160=304÷100×10=30.4。
(2) 8.3×4的积有( 一 )位小数,32.4×0.26的积有
( 三 )位小数。
解析:8.3和4一共有一位小数,则它们的积有一位小数;32.4和
0.26一共有三位小数,则它们的积有三位小数。
一
三
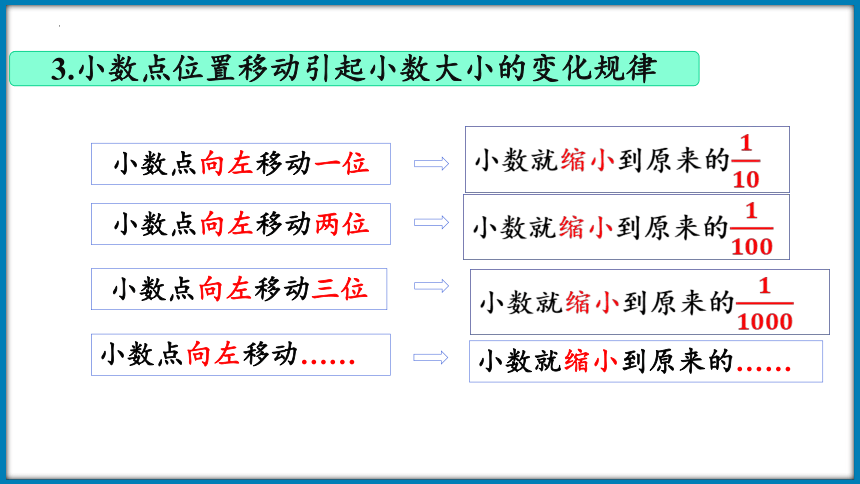
小数点向左移动一位
小数就缩小到原来的
小数点向左移动两位
小数就缩小到原来的
小数点向左移动三位
小数就缩小到原来的
小数点向左移动……
小数就缩小到原来的……
3.小数点位置移动引起小数大小的变化规律
小数点向右移动一位
小数就扩大到原来的10倍
小数点向右移动两位
小数就扩大到原来的100倍
小数点向右移动三位
小数就扩大到原来的1000倍
小数点向右移动……
小数就扩大到原来的……
3.小数点位置移动引起小数大小的变化规律
(1) 把0.5的小数点向左移动一位,得到的数是它的
( );把0.09的小数点向右移动一位,得到的数是它
的( 10倍 )。
解析:把0.5的小数点向左移动一位,就是缩小到原来的,即得到的数是它的;把0.09的小数点向右移动一位,就是扩大到原来的10倍,即得到的数是它的10倍。
10倍
(2) 0.06是6的( ),8是0.008的( 1000 )。
解析:6的小数点向左移动两位变成0.06,则0.06是6的;0.008的小数点向右移动三位是8,则8是0.008的1000倍。
1000
(3) 把0.75扩大到它的100倍是( 75 );把20缩小到它的
是( 0.02 )。
解析:把0.75扩大到它的100倍,即小数点向右移动两位,是75;
把20缩小到它的,即小数点向左移动三位,是0.02。
75
0.02
两个数相乘,一个乘数扩大到原来的m倍,另一个乘数扩大到原来的n倍,那么积就扩大到原来定的(m×n)倍,反之,一个乘数缩小到原来的 ,另一个乘数缩小到原来的 ,那么积就缩小到原来的 。
4.积的小数位数与乘数的小数位数的关系
积的小数位数等于乘数的小数位数之和。
可以据此检验积的小数点的位置是否正确。
4.积的小数位数与乘数的小数位数的关系
(1)16×3的积是( 48 ),把16缩小到它的,把3缩小到
它的,所得的积就缩小到原来的( ),是
( 0.048 )。
48
0.048
(2)两个乘数的积是2.75,如果其中一个乘数扩大到原来的
10倍,另一个乘数缩小到原来的,那么所得的积是
( 0.275 )。
解析:一个乘数扩大到原来的10倍,另一个乘数缩小到原来的
,积就缩小到原来的,则所得的积是2.75÷10=0.275。
0.275
(3) 根据18×56=1008,在括号里填上合适的数。
1.8×5.6=( 10.08 )
0.18×( 5.6 )=1.008
( 0.018 )×56=1.008
解析:积的末尾没有0时,看乘数中一共有几位小数,积就是几位小数,根据此规律和所给算式直接写出积和其中的一个乘数。
10.08
5.6
0.018
当一个乘数大于1时,积大于另一个不为零的乘数;
当一个乘数小于1时,积小于另一个不为零的乘数;当一个乘数等于1时,积等于另一个乘数。
5.积和乘数(0除外)的大小关系
(1) 在 里填上“>”“<”或“=”。
21×0.99 < 21
2.01×4.27 > 4.27
7.83×0.85 < 7.83×1.01
13.4×0.8 = 1.34×8
<
>
<
=
(2)小华在计算2.5×0.23=5.075时,看到算得的结果想了想
说:“我肯定算错了”,他判断的依据是( B )。
A.积应该比0.23小
B.积应该比2.5小
C.积应该比2.5大
解析:一个非0的数乘小于1的数,积小于原数,所以2.5×0.23的积小于2.5。
B
1.小数的加、减、乘混合运算的运算顺序与整数混合运算的运算顺序 相同。在一个算式里,如果既有乘法又有加法,要先算乘法,后算加减法;如果只有乘法,要按照从左到右的顺序以此计算;有括号的要先算括号里面的,再算括号外面的。
整数乘法的运算律对小数乘法同样适用,使用运算律可以使一些计算更简便。
6.小数的加、减、乘混合运算
老师告诉你:
小数乘法的简便计算和整数乘法基本一样,主要利用
乘法的运算定律和运算性质以及积的变化规律,通过对算
式进行适当变形,将其中的数转化成整数、整十数、整百
数……或者使计算中的一些数变得易于口算,从而使计算
简便。
简算:0.9999×1.8-0.1111×7.2
例
思路分析:0.9999是0.1111的9倍,可以将0.9999转化成0.1111,则另一个乘数1.8就要乘9得16.2;也可以将0.1111转化成0.9999,则另一个乘数7.2就要除以9得0.8。经过转化,这道题就可以用乘法分配律来计算了。
解法一:
0.9999×1.8-0.1111×7.2
=0.1111×9×1.8-0.1111×7.2
=0.1111×(16.2-7.2)
=0.1111×9
=0.9999
规范解答:
解法二:
0.9999×1.8-0.1111×7.2
=0.9999×1.8-0.1111×9×0.8
=0.9999×(1.8-0.8)
=0.9999
技巧1
运用乘法分配律简算
1.用简便方法计算下面各题。
=9.9×13.6
=(10-0.1)×13.6
=10×13.6-0.1×13.6
=136-1.36
=134.64
=6.59×2.45+7.55×6.59
=6.59×(2.45+7.55)
=6.59×10
=65.9
=4.2×1.01
=4.2×(1+0.01)
=4.2×1+4.2×0.01
=4.2+0.042
=4.242
=45×2.1-5×2.1
=(45-5)×2.1
=40×2.1
=84
技巧2
综合运用乘法运算律简算
2.用两种不同的方法简算。 (方法不唯一)
(1)1.25×7.2
方法一: 1.25×7.2
=1.25×8×0.9
=10×0.9
=9
(方法不唯一)
方法二: 1.25×7.2
=1.25×(8-0.8)
=1.25×8-1.25×0.8
=10-1
=9
技巧3
运用转化思想简算
3.简算。
=0.55×0.6+0.11×7
=0.11×3+0.11×7
=0.11×(3+7)
=0.11×10
=1.1
=0.99×10.1-9.9×0.01
=0.99×10.1-0.99×0.1
=0.99×(10.1-0.1)
=0.99×10
=9.9
=11×22+0.22×3300+660×2.2
=11×22+22×33+66×22
=(11+33+66)×22
=110×22
=2420
=1.99+199×0.99
=1.99+1.99×99
=1.99×(1+99)
=1.99×100
=199
技巧4
根据数的特点通过变形简算
4.简算: 2024×2023.2023-2023×2024.2024
=2024×2023×1.0001-2023×2024×1.0001
=0
1.填一填。
(1)3.75扩大到它的10倍是( 37.5 ),扩大到它的100倍
是( 375 )。
(2)1250缩小到它的是( 125 ),缩小到它的是
( 12.5 )。
(3)把0.1978的小数点先向右移动三位,再向左移动一位后
是( 19.78 )。
(4)23×1.7=39.1,则2.3×0.17=( 0.391 )。
37.5
375
125
12.5
19.78
0.391
课堂练习
2.涂一涂,算一算。
0.04×5=0.2 0.2×3=0.6
0.2
0.6
点解析:把1个大正方形平均分成了100份,每个小格表示0.01,4个小格表示0.04,4×5=20(个)小格就是0.2,所以0.04×5=0.2;0.2表示2个0.1,也表示20个0.01,0.2×3是(3×20)个0.01,即0.6。
3.列竖式计算下列各题。
5.04×28
3.82×0.45
0.96×6.9
5.0 4
× 2 8
4 0 3 2
1 0 0 8
1 4 1 1 2
=141.12
3.8 2
×0.4 5
1 9 1 0
1 5 2 8
1 7 1 9 0
8 6 4
5 7 6
6 6 2 4
0.9 6
× 6.9
=6.624
=1.719
4.根据如图计算2.8×3.4的积。(填一填)
2
0.8 + 0.32 + 6 + 2.4 = 9.52
2
0.4
0.8
0.8
0.4
0.32
2
3
6
0.8
3
2.4
0.8
0.32
6
2.4
9.52
5.电动汽车行驶1千米只需耗电0.15千瓦时,每千瓦时电
费是0.8元。电动汽车行驶100千米需耗电费多少元?行驶
同样的路程,汽油车的耗油费大约是电动汽车耗电费的5.4倍,汽油车行驶100千米大约需耗油费多少元?
电动汽车:0.15×0.8×100=12(元)
汽油车:12×5.4=64.8(元)
答:电动汽车行驶100千米需耗电费12元。汽油车行驶
100千米大约需耗油费64.8元。
6.如果一只仓鼠1时能跑0.98千米,照这样计算,仓鼠
连续跑2天能不能跑完一个全程马拉松?(一个全程马
拉松长42195米)
1天=24时
0.98×24×2=47.04(千米)
47.04千米=47040米
47040>42195
答:仓鼠连续跑2天能跑完一个全程马拉松。
老师告诉你:
在生活中,我们经常要用小数乘法解决实际问题,
如分段计算出租车费、分段计算水电费、分段计算邮资
费等。解答这类问题的基本方法是用以内的费用加以外
的费用。
某市出租车收费标准如下:3千米及3千米以内7
元,超过3千米的部分按每千米1.2元收费(不足1千米按1千米计算)。妈妈打车去离家7.4千米的超市,她应付车费多少元?
例
思路分析:根据收费标准规定,乘车7.4千米要按8千米计费。再将8千米分成3千米及3千米以内的部分和3千米以外的部分进行计算。
规范解答: 7.4千米≈8千米
8=3+5 7+5×1.2=13(元)
答:她应付车费13元。
7.某市去年7月起,对用电实行阶梯式收费。实施阶梯电价后,分三级计算每月电费,具体见右表。
类别 每月每户用电量/千瓦时 电价标准/(元/千瓦时)
第一级 0~240(含) 0.57
第二级 240~400(含) 0.62
第三级 400以上 0.87
(1)小芳家上个月的用电量为270千瓦时,电费是多少元?
(270-240)×0.62+240×0.57=155.4(元)
答:电费是155.4元。
(2)小明家上个月的用电量为428千瓦时,电费是多少元?
(428-400)×0.87+(400-240)×0.62+240×0.57=
260.36(元)
答:电费是260.36元。
8.邮局邮寄信函的收费标准如右表。
计费标准 收费标准/元
本埠 外埠
100克及以内的,每20克 (不足20克,按20克计算) 0.80 1.20
100克以上部分,每增加100克加收 (不足100克,按100克计算) 1.20 2.00
(1)小亮要给本埠的老师寄一封156克的信函,应付邮资费
多少元?
156-100=56(克)
56克不足100克按100克计算,计费1.20元。
0.80×(100÷20)+1.20=5.2(元)
答:应付邮资费5.2元。
(2)小玲要给外埠的姑姑寄一封258克的信函,应付邮资费
多少元?
258-100=158(克)
158克按200克计费,2×2=4(元)。
1.20×(100÷20)+4=10(元)
答:应付邮资费10元。
北师版四年级数学下册
小数乘法
复习与整理
汇报人:XXX 时间:XXXXX
小组交流:本单元主要学习了哪些内容?
小数乘法
小数乘整数
小数乘小数
加、减、乘混合运算
规律
小数点移动引起小数大小变化的规律
积的小数位数与乘数的小数位数的关系
积和乘数(0除外)的大小关系
知识梳理
1. 小数乘整数的意义和整数乘法的意义相同,都是
求几个相同加数的和的简便运算;也可以说是求
这个小数的整数倍是多少。
2. 计算简单的小数乘整数,可以根据乘法的意义用
连加来计算;也可以转化成整数乘法来计算;也
可以借助直观示意图来计算。
1.小数乘整数
知识回顾
(1) 0.9×3=( 0.9 )+( 0.9 )+( 0.9 )(填相同的数)
解析:0.9×3可以表示3个0.9相加,即0.9+0.9+0.9。
(2) 0.8×4表示( 4个0.8相加是多少(或0.8的4倍是多 ),结果是( 3.2 )。
0.9
0.9
0.9
4个0.8相加是多少(或0.8的4倍是多少)
3.2
小数乘法的计算方法:先按照整数乘法的计算方法算出积,再看乘数中一共有几位小数,就从积的右边起数出几位,点上小数点。
积的位数不够时,先在积的左边添0补位,再点上小数点。
知识回顾
2.小数乘小数
(1) 根据19×16=304,在括号里填上适当的数。
①19×( 0.16 )=3.04
②( 0.19 )×1.6=0.304
③0.19×160=( 30.4 )
0.16
0.19
30.4
解析:①积是两位小数,两个乘数中一共应有两位小数,则括号中
的数是两位小数,是0.16;②积是三位小数,两个乘数中一共应有
三位小数,而乘数“1.6”是一位小数,则括号中的数应是两位小
数,是0.19;③19缩小到原来的是0.19,16扩大到原来的10倍是
160,则0.19×160=304÷100×10=30.4。
(2) 8.3×4的积有( 一 )位小数,32.4×0.26的积有
( 三 )位小数。
解析:8.3和4一共有一位小数,则它们的积有一位小数;32.4和
0.26一共有三位小数,则它们的积有三位小数。
一
三
小数点向左移动一位
小数就缩小到原来的
小数点向左移动两位
小数就缩小到原来的
小数点向左移动三位
小数就缩小到原来的
小数点向左移动……
小数就缩小到原来的……
3.小数点位置移动引起小数大小的变化规律
小数点向右移动一位
小数就扩大到原来的10倍
小数点向右移动两位
小数就扩大到原来的100倍
小数点向右移动三位
小数就扩大到原来的1000倍
小数点向右移动……
小数就扩大到原来的……
3.小数点位置移动引起小数大小的变化规律
(1) 把0.5的小数点向左移动一位,得到的数是它的
( );把0.09的小数点向右移动一位,得到的数是它
的( 10倍 )。
解析:把0.5的小数点向左移动一位,就是缩小到原来的,即得到的数是它的;把0.09的小数点向右移动一位,就是扩大到原来的10倍,即得到的数是它的10倍。
10倍
(2) 0.06是6的( ),8是0.008的( 1000 )。
解析:6的小数点向左移动两位变成0.06,则0.06是6的;0.008的小数点向右移动三位是8,则8是0.008的1000倍。
1000
(3) 把0.75扩大到它的100倍是( 75 );把20缩小到它的
是( 0.02 )。
解析:把0.75扩大到它的100倍,即小数点向右移动两位,是75;
把20缩小到它的,即小数点向左移动三位,是0.02。
75
0.02
两个数相乘,一个乘数扩大到原来的m倍,另一个乘数扩大到原来的n倍,那么积就扩大到原来定的(m×n)倍,反之,一个乘数缩小到原来的 ,另一个乘数缩小到原来的 ,那么积就缩小到原来的 。
4.积的小数位数与乘数的小数位数的关系
积的小数位数等于乘数的小数位数之和。
可以据此检验积的小数点的位置是否正确。
4.积的小数位数与乘数的小数位数的关系
(1)16×3的积是( 48 ),把16缩小到它的,把3缩小到
它的,所得的积就缩小到原来的( ),是
( 0.048 )。
48
0.048
(2)两个乘数的积是2.75,如果其中一个乘数扩大到原来的
10倍,另一个乘数缩小到原来的,那么所得的积是
( 0.275 )。
解析:一个乘数扩大到原来的10倍,另一个乘数缩小到原来的
,积就缩小到原来的,则所得的积是2.75÷10=0.275。
0.275
(3) 根据18×56=1008,在括号里填上合适的数。
1.8×5.6=( 10.08 )
0.18×( 5.6 )=1.008
( 0.018 )×56=1.008
解析:积的末尾没有0时,看乘数中一共有几位小数,积就是几位小数,根据此规律和所给算式直接写出积和其中的一个乘数。
10.08
5.6
0.018
当一个乘数大于1时,积大于另一个不为零的乘数;
当一个乘数小于1时,积小于另一个不为零的乘数;当一个乘数等于1时,积等于另一个乘数。
5.积和乘数(0除外)的大小关系
(1) 在 里填上“>”“<”或“=”。
21×0.99 < 21
2.01×4.27 > 4.27
7.83×0.85 < 7.83×1.01
13.4×0.8 = 1.34×8
<
>
<
=
(2)小华在计算2.5×0.23=5.075时,看到算得的结果想了想
说:“我肯定算错了”,他判断的依据是( B )。
A.积应该比0.23小
B.积应该比2.5小
C.积应该比2.5大
解析:一个非0的数乘小于1的数,积小于原数,所以2.5×0.23的积小于2.5。
B
1.小数的加、减、乘混合运算的运算顺序与整数混合运算的运算顺序 相同。在一个算式里,如果既有乘法又有加法,要先算乘法,后算加减法;如果只有乘法,要按照从左到右的顺序以此计算;有括号的要先算括号里面的,再算括号外面的。
整数乘法的运算律对小数乘法同样适用,使用运算律可以使一些计算更简便。
6.小数的加、减、乘混合运算
老师告诉你:
小数乘法的简便计算和整数乘法基本一样,主要利用
乘法的运算定律和运算性质以及积的变化规律,通过对算
式进行适当变形,将其中的数转化成整数、整十数、整百
数……或者使计算中的一些数变得易于口算,从而使计算
简便。
简算:0.9999×1.8-0.1111×7.2
例
思路分析:0.9999是0.1111的9倍,可以将0.9999转化成0.1111,则另一个乘数1.8就要乘9得16.2;也可以将0.1111转化成0.9999,则另一个乘数7.2就要除以9得0.8。经过转化,这道题就可以用乘法分配律来计算了。
解法一:
0.9999×1.8-0.1111×7.2
=0.1111×9×1.8-0.1111×7.2
=0.1111×(16.2-7.2)
=0.1111×9
=0.9999
规范解答:
解法二:
0.9999×1.8-0.1111×7.2
=0.9999×1.8-0.1111×9×0.8
=0.9999×(1.8-0.8)
=0.9999
技巧1
运用乘法分配律简算
1.用简便方法计算下面各题。
=9.9×13.6
=(10-0.1)×13.6
=10×13.6-0.1×13.6
=136-1.36
=134.64
=6.59×2.45+7.55×6.59
=6.59×(2.45+7.55)
=6.59×10
=65.9
=4.2×1.01
=4.2×(1+0.01)
=4.2×1+4.2×0.01
=4.2+0.042
=4.242
=45×2.1-5×2.1
=(45-5)×2.1
=40×2.1
=84
技巧2
综合运用乘法运算律简算
2.用两种不同的方法简算。 (方法不唯一)
(1)1.25×7.2
方法一: 1.25×7.2
=1.25×8×0.9
=10×0.9
=9
(方法不唯一)
方法二: 1.25×7.2
=1.25×(8-0.8)
=1.25×8-1.25×0.8
=10-1
=9
技巧3
运用转化思想简算
3.简算。
=0.55×0.6+0.11×7
=0.11×3+0.11×7
=0.11×(3+7)
=0.11×10
=1.1
=0.99×10.1-9.9×0.01
=0.99×10.1-0.99×0.1
=0.99×(10.1-0.1)
=0.99×10
=9.9
=11×22+0.22×3300+660×2.2
=11×22+22×33+66×22
=(11+33+66)×22
=110×22
=2420
=1.99+199×0.99
=1.99+1.99×99
=1.99×(1+99)
=1.99×100
=199
技巧4
根据数的特点通过变形简算
4.简算: 2024×2023.2023-2023×2024.2024
=2024×2023×1.0001-2023×2024×1.0001
=0
1.填一填。
(1)3.75扩大到它的10倍是( 37.5 ),扩大到它的100倍
是( 375 )。
(2)1250缩小到它的是( 125 ),缩小到它的是
( 12.5 )。
(3)把0.1978的小数点先向右移动三位,再向左移动一位后
是( 19.78 )。
(4)23×1.7=39.1,则2.3×0.17=( 0.391 )。
37.5
375
125
12.5
19.78
0.391
课堂练习
2.涂一涂,算一算。
0.04×5=0.2 0.2×3=0.6
0.2
0.6
点解析:把1个大正方形平均分成了100份,每个小格表示0.01,4个小格表示0.04,4×5=20(个)小格就是0.2,所以0.04×5=0.2;0.2表示2个0.1,也表示20个0.01,0.2×3是(3×20)个0.01,即0.6。
3.列竖式计算下列各题。
5.04×28
3.82×0.45
0.96×6.9
5.0 4
× 2 8
4 0 3 2
1 0 0 8
1 4 1 1 2
=141.12
3.8 2
×0.4 5
1 9 1 0
1 5 2 8
1 7 1 9 0
8 6 4
5 7 6
6 6 2 4
0.9 6
× 6.9
=6.624
=1.719
4.根据如图计算2.8×3.4的积。(填一填)
2
0.8 + 0.32 + 6 + 2.4 = 9.52
2
0.4
0.8
0.8
0.4
0.32
2
3
6
0.8
3
2.4
0.8
0.32
6
2.4
9.52
5.电动汽车行驶1千米只需耗电0.15千瓦时,每千瓦时电
费是0.8元。电动汽车行驶100千米需耗电费多少元?行驶
同样的路程,汽油车的耗油费大约是电动汽车耗电费的5.4倍,汽油车行驶100千米大约需耗油费多少元?
电动汽车:0.15×0.8×100=12(元)
汽油车:12×5.4=64.8(元)
答:电动汽车行驶100千米需耗电费12元。汽油车行驶
100千米大约需耗油费64.8元。
6.如果一只仓鼠1时能跑0.98千米,照这样计算,仓鼠
连续跑2天能不能跑完一个全程马拉松?(一个全程马
拉松长42195米)
1天=24时
0.98×24×2=47.04(千米)
47.04千米=47040米
47040>42195
答:仓鼠连续跑2天能跑完一个全程马拉松。
老师告诉你:
在生活中,我们经常要用小数乘法解决实际问题,
如分段计算出租车费、分段计算水电费、分段计算邮资
费等。解答这类问题的基本方法是用以内的费用加以外
的费用。
某市出租车收费标准如下:3千米及3千米以内7
元,超过3千米的部分按每千米1.2元收费(不足1千米按1千米计算)。妈妈打车去离家7.4千米的超市,她应付车费多少元?
例
思路分析:根据收费标准规定,乘车7.4千米要按8千米计费。再将8千米分成3千米及3千米以内的部分和3千米以外的部分进行计算。
规范解答: 7.4千米≈8千米
8=3+5 7+5×1.2=13(元)
答:她应付车费13元。
7.某市去年7月起,对用电实行阶梯式收费。实施阶梯电价后,分三级计算每月电费,具体见右表。
类别 每月每户用电量/千瓦时 电价标准/(元/千瓦时)
第一级 0~240(含) 0.57
第二级 240~400(含) 0.62
第三级 400以上 0.87
(1)小芳家上个月的用电量为270千瓦时,电费是多少元?
(270-240)×0.62+240×0.57=155.4(元)
答:电费是155.4元。
(2)小明家上个月的用电量为428千瓦时,电费是多少元?
(428-400)×0.87+(400-240)×0.62+240×0.57=
260.36(元)
答:电费是260.36元。
8.邮局邮寄信函的收费标准如右表。
计费标准 收费标准/元
本埠 外埠
100克及以内的,每20克 (不足20克,按20克计算) 0.80 1.20
100克以上部分,每增加100克加收 (不足100克,按100克计算) 1.20 2.00
(1)小亮要给本埠的老师寄一封156克的信函,应付邮资费
多少元?
156-100=56(克)
56克不足100克按100克计算,计费1.20元。
0.80×(100÷20)+1.20=5.2(元)
答:应付邮资费5.2元。
(2)小玲要给外埠的姑姑寄一封258克的信函,应付邮资费
多少元?
258-100=158(克)
158克按200克计费,2×2=4(元)。
1.20×(100÷20)+4=10(元)
答:应付邮资费10元。
