第五章 相交线与平行线综合练习(含答案)2023-2024学人教版七年级数学下册
文档属性
| 名称 | 第五章 相交线与平行线综合练习(含答案)2023-2024学人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 00:00:00 | ||
图片预览




文档简介
第五章 相交线与平行线 综合练习
一.选择题(共12小题)
1.如图,下列推理中正确的是( )
A.∵∠1=∠4,∴AD∥BC
B.∵∠2=∠3,∴AD∥BC
C.∵∠A+∠ABC=180°,∴AB∥DC
D.∵∠C+∠ABC=180°,∴AD∥BC
2.下列命题中,属于假命题的是( )
A.如果a,b都是正数,那么ab>0
B.如果a2=b2,那么a=b
C.如果一个三角形是直角三角形,那么它的两个锐角互余
D.同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
3.如图,已知直线a∥b,∠1=105°,则∠2等于( )
A.65° B.75° C.85° D.105°
4.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列命题中,属于假命题的是( )
A.若∠C=∠A+∠B,则△ABC是直角三角形
B.若c2=b2﹣a2,则△ABC是直角三角形,且∠C=90°
C.若(c+a)(c﹣a)=b2,则△ABC是直角三角形
D.若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
5.小明将一块直角三角板摆放在直尺上,如图所示,∠ABC=25°,则∠DEF的度数是( )
A.35° B.45° C.55° D.65°
6.有下列说法:①射线AB与射线BA表示同一条射线;②若线段AB=BC,则点B是线段AC的中点;③两点确定一条直线;④两点之间,线段最短;⑤对顶角相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠DAB+∠ABC=180° D.∠B=∠D
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,则∠DBC的大小为( )
A.10° B.15° C.18° D.12°
9.下列命题,正确的是( )
A.三角形三条中线的交点到三角形三个顶点的距离相等
B.三角形三条高线的交点到三角形三个顶点的距离相等
C.三角形三条角平分线的交点到三角形三个顶点的距离相等
D.三角形三边中垂线的交点到三角形三个顶点的距离相等
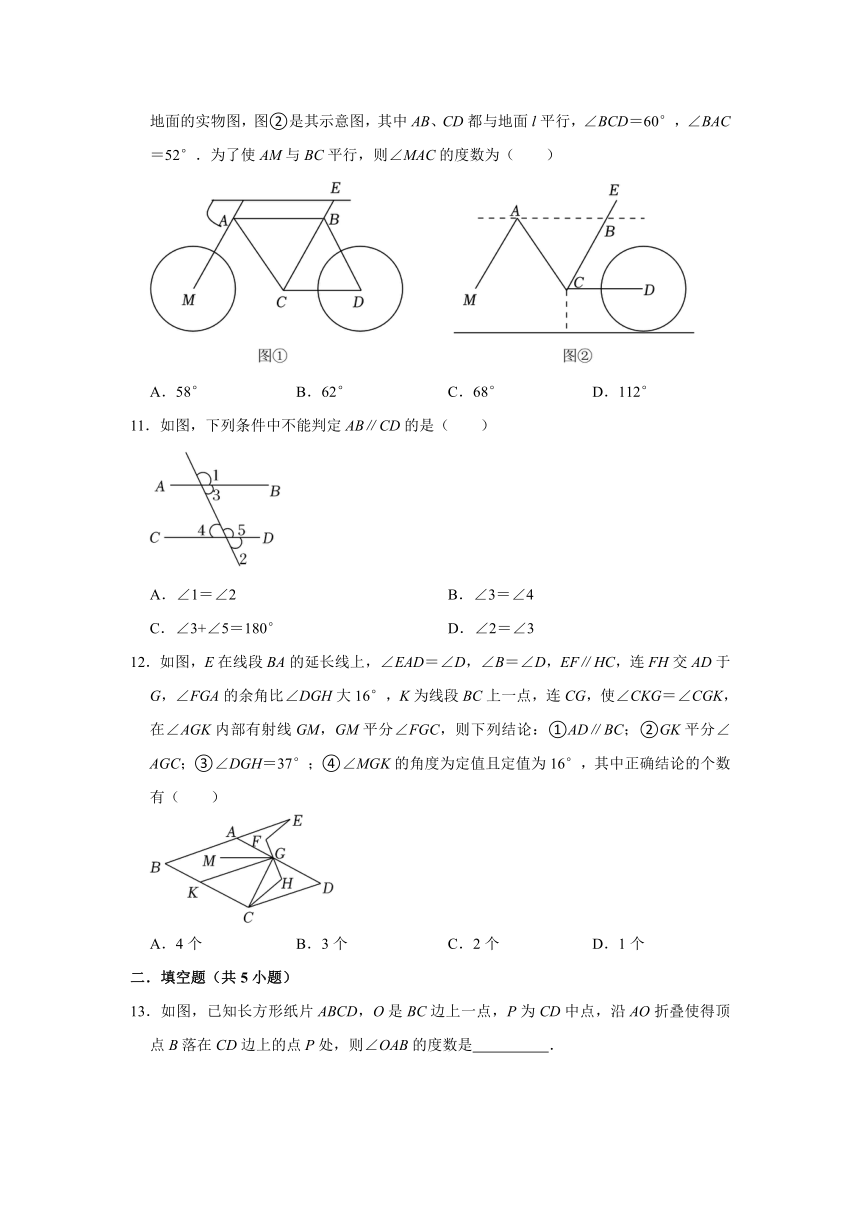
10.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB、CD都与地面l平行,∠BCD=60°,∠BAC=52°.为了使AM与BC平行,则∠MAC的度数为( )
A.58° B.62° C.68° D.112°
11.如图,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠3+∠5=180° D.∠2=∠3
12.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠DGH=37°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共5小题)
13.如图,已知长方形纸片ABCD,O是BC边上一点,P为CD中点,沿AO折叠使得顶点B落在CD边上的点P处,则∠OAB的度数是 .
14.东北育才学校初一学生小白参加某次数学竞赛,单选题得分规则如下:每道题共有4个选项,答错得0分,答对得4分,不答对得1分.小白发现第3个单选题A选项必错,其他选项把握不准,此题不答(记为①)和从除A外的三个选项中随机选择一个(记为②),哪种方法对小白更有利?请填序号 .
15.甲、乙、丙、丁、戊五个同学是好朋友,一次郊游时都已口渴难耐,却只剩下两个梨,大家相互推让:
甲说:“如果我吃一个,那么乙也应吃一个”;
乙说:“如果我吃一个,那么丙也应吃一个”;
丙说:“如果我吃一个,那么丁也应吃一个”;
丁说:“如果我吃一个,那么戊也应吃一个”;
大家都遵守诺言,两个梨均被吃掉,请问:哪两个人吃掉了这两个梨? .
16.如图,已知∠MAB是锐角,BN⊥AM,BN=1cm,AB=2cm.点C是射线AM上的一个动点.利用图形画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题.你画图时,BC长可选取的范围是 cm.若△ABC的形状、大小是唯一确定的,则BC的取值范围是 .
17.如图,已知∠1+∠2=180°,且∠3=∠B,
若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE=______
三.解答题(共5小题)
18.如图,已知直线l1∥l2,直线l和直线l1、l2交于点C和D,在C、D之间有一点P,A是l1上的一点,B是l2上的一点.
(1)如果P点在C、D之间运动时,如图(1)问∠PAC,∠APB,∠PBD之间有何关系,并说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),在图(2),图(3)中画出图形并探索∠PAC,∠APB,∠PBD之间的关系又是如何?并选择其中一种情况说明理由.
19.如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA、PB,构成∠PAV、∠APB、∠PBD三个角.
(1)当动点P落在第①部分时,如图1,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?在图2中画出图形,若成立,写出推理过程,若不成立,直线写出这三个角之间的关系;
(3)当动点P落在第③部分时,延长BA,点P在射线BA的左侧和右侧时,分别探究∠PAC、∠APB、∠PBD之间关系,在图3中画出图形,并直接写出相应的结论.
20.在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,当点M在线段AC上,且∠C=50°时,求证BD∥MF;
(2)当点M在边AC的延长线上时,补全图②,判断BD与MF的位置关系并证明.
21.如图,在正方形网格中有一个三角形ABC,图中每一个小正方形边长为1,按要求完成下列各题:
(1)将三角形ABC向右平移2格,再向上平移3格后得到三角形DEF,画出三角形DEF;
(2)求三角形DEF的面积.
22.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为 °
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数.
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
参考答案
一.选择题(共12小题)
1---10BBBBD CABDC 11--12AB
二.填空题(共5小题)
13.30°
14.②
15.丁和戊
16.BC=1cm或BC≥2cm.
17.70°
三.解答题(共5小题)
18.解:(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:过点P作PE∥l1,
∵l1∥l2
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
19.解:(1)延长AP交BD于M,如图1,
∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD.
(2)∠APB=∠PAC+∠PBD不成立,如图2,
理由是:过P作EF∥AC,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180°,∠PBD+∠BPF=180°,
∴∠PAC+∠APF+∠PBD+∠BPF=360°,
∴∠APB+∠PAC+∠PBD=360°,
∴∠APB=360°﹣∠PAC﹣∠PBD,
∵∠APB≠180°,
∴∠APB=∠PAC+∠PBD不成立.
(3)①当动点P在射线BA的右侧时,如图3,结论是∠PBD=∠PAC+∠APB,
理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PMC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
②当动点P在射线BA上时,如图4,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),
理由是:∵AC∥BD,
∴∠PAC=∠PBD,
∵∠APB=0°,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB.
③当动点P在射线BA的左侧时,如图5,结论是:∠PAC=∠APB+∠PBD,
理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PAC=∠APB+∠PMC,
∴∠PAC=∠APB+∠PBD.
20.(1)证明:∵∠A=90°,∠C=50°,BD平分∠ABC,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣90°﹣50°=40°,
∴∠ADB=∠CBD+∠C=∠ABC+∠C=×40°+50°=70°.
∵∠AME=∠C+∠MEC=50°+90°=140°,MF为∠AME的平分线,
∴∠AMF=∠AME=×140°=70°,
∴∠ADB=∠AMF=70°,
∴BD∥MF.
(2)M是AC延长线上的一点,过点M作ME⊥BC,交BC延长线于点E,过点M作∠AME平分线MF,交BA延长线于点F.
判断BD⊥MF.
证明:延长BD,交MF于点G.
∵在Rt△ABC和Rt△CMF中,∠BAC=∠CEM,∠BCA=∠MCE,
∴∠ABC=∠CME.
又∵BD、MF分别为∠ABC和∠CME的平分线,
∴∠FBG=∠AMF.
又∵∠AMF+∠AFM=90°,
∴∠FBG+∠AFM=90°,
∴∠BGF=90°,
∴BD⊥MF.
21.解:(1)如图所示:△DEF即为所求;
(2)△DEF的面积为:×2×3=3.
22.解:(1)设∠H的4系补周角的度数为x°,根据新定义得,120+4x=360,
解得,x=60,
∠H的4系补周角的度数为60°,
故答案为60;
(2)①过E作EF∥AB,如图1,
∴∠B=∠BEF,
∵AB∥CD,
∴EF∥CD,∠D=60°,
∴∠D=∠DEF=60°,
∵∠B+60°=∠BEF+∠DEF,
即∠B+60°=∠BED,
∵∠B是∠BED的3系补周角,
∴∠BED=360°﹣3∠B,
∴∠B+60°=360°﹣3∠B,
∴∠B=75°;
②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n
一.选择题(共12小题)
1.如图,下列推理中正确的是( )
A.∵∠1=∠4,∴AD∥BC
B.∵∠2=∠3,∴AD∥BC
C.∵∠A+∠ABC=180°,∴AB∥DC
D.∵∠C+∠ABC=180°,∴AD∥BC
2.下列命题中,属于假命题的是( )
A.如果a,b都是正数,那么ab>0
B.如果a2=b2,那么a=b
C.如果一个三角形是直角三角形,那么它的两个锐角互余
D.同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
3.如图,已知直线a∥b,∠1=105°,则∠2等于( )
A.65° B.75° C.85° D.105°
4.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列命题中,属于假命题的是( )
A.若∠C=∠A+∠B,则△ABC是直角三角形
B.若c2=b2﹣a2,则△ABC是直角三角形,且∠C=90°
C.若(c+a)(c﹣a)=b2,则△ABC是直角三角形
D.若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
5.小明将一块直角三角板摆放在直尺上,如图所示,∠ABC=25°,则∠DEF的度数是( )
A.35° B.45° C.55° D.65°
6.有下列说法:①射线AB与射线BA表示同一条射线;②若线段AB=BC,则点B是线段AC的中点;③两点确定一条直线;④两点之间,线段最短;⑤对顶角相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠DAB+∠ABC=180° D.∠B=∠D
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,则∠DBC的大小为( )
A.10° B.15° C.18° D.12°
9.下列命题,正确的是( )
A.三角形三条中线的交点到三角形三个顶点的距离相等
B.三角形三条高线的交点到三角形三个顶点的距离相等
C.三角形三条角平分线的交点到三角形三个顶点的距离相等
D.三角形三边中垂线的交点到三角形三个顶点的距离相等
10.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB、CD都与地面l平行,∠BCD=60°,∠BAC=52°.为了使AM与BC平行,则∠MAC的度数为( )
A.58° B.62° C.68° D.112°
11.如图,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠3+∠5=180° D.∠2=∠3
12.如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠DGH=37°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共5小题)
13.如图,已知长方形纸片ABCD,O是BC边上一点,P为CD中点,沿AO折叠使得顶点B落在CD边上的点P处,则∠OAB的度数是 .
14.东北育才学校初一学生小白参加某次数学竞赛,单选题得分规则如下:每道题共有4个选项,答错得0分,答对得4分,不答对得1分.小白发现第3个单选题A选项必错,其他选项把握不准,此题不答(记为①)和从除A外的三个选项中随机选择一个(记为②),哪种方法对小白更有利?请填序号 .
15.甲、乙、丙、丁、戊五个同学是好朋友,一次郊游时都已口渴难耐,却只剩下两个梨,大家相互推让:
甲说:“如果我吃一个,那么乙也应吃一个”;
乙说:“如果我吃一个,那么丙也应吃一个”;
丙说:“如果我吃一个,那么丁也应吃一个”;
丁说:“如果我吃一个,那么戊也应吃一个”;
大家都遵守诺言,两个梨均被吃掉,请问:哪两个人吃掉了这两个梨? .
16.如图,已知∠MAB是锐角,BN⊥AM,BN=1cm,AB=2cm.点C是射线AM上的一个动点.利用图形画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题.你画图时,BC长可选取的范围是 cm.若△ABC的形状、大小是唯一确定的,则BC的取值范围是 .
17.如图,已知∠1+∠2=180°,且∠3=∠B,
若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE=______
三.解答题(共5小题)
18.如图,已知直线l1∥l2,直线l和直线l1、l2交于点C和D,在C、D之间有一点P,A是l1上的一点,B是l2上的一点.
(1)如果P点在C、D之间运动时,如图(1)问∠PAC,∠APB,∠PBD之间有何关系,并说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),在图(2),图(3)中画出图形并探索∠PAC,∠APB,∠PBD之间的关系又是如何?并选择其中一种情况说明理由.
19.如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA、PB,构成∠PAV、∠APB、∠PBD三个角.
(1)当动点P落在第①部分时,如图1,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?在图2中画出图形,若成立,写出推理过程,若不成立,直线写出这三个角之间的关系;
(3)当动点P落在第③部分时,延长BA,点P在射线BA的左侧和右侧时,分别探究∠PAC、∠APB、∠PBD之间关系,在图3中画出图形,并直接写出相应的结论.
20.在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,当点M在线段AC上,且∠C=50°时,求证BD∥MF;
(2)当点M在边AC的延长线上时,补全图②,判断BD与MF的位置关系并证明.
21.如图,在正方形网格中有一个三角形ABC,图中每一个小正方形边长为1,按要求完成下列各题:
(1)将三角形ABC向右平移2格,再向上平移3格后得到三角形DEF,画出三角形DEF;
(2)求三角形DEF的面积.
22.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为 °
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数.
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
参考答案
一.选择题(共12小题)
1---10BBBBD CABDC 11--12AB
二.填空题(共5小题)
13.30°
14.②
15.丁和戊
16.BC=1cm或BC≥2cm.
17.70°
三.解答题(共5小题)
18.解:(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:过点P作PE∥l1,
∵l1∥l2
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
19.解:(1)延长AP交BD于M,如图1,
∵AC∥BD,
∴∠PAC=∠AMB,
∵∠APB=∠AMB+∠PBD,
∴∠APB=∠PAC+∠PBD.
(2)∠APB=∠PAC+∠PBD不成立,如图2,
理由是:过P作EF∥AC,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠PAC+∠APF=180°,∠PBD+∠BPF=180°,
∴∠PAC+∠APF+∠PBD+∠BPF=360°,
∴∠APB+∠PAC+∠PBD=360°,
∴∠APB=360°﹣∠PAC﹣∠PBD,
∵∠APB≠180°,
∴∠APB=∠PAC+∠PBD不成立.
(3)①当动点P在射线BA的右侧时,如图3,结论是∠PBD=∠PAC+∠APB,
理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PMC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
②当动点P在射线BA上时,如图4,结论是:∠PBD=∠PAC+∠APB(或∠PAC=∠PBD+∠APB或∠APB=0°),
理由是:∵AC∥BD,
∴∠PAC=∠PBD,
∵∠APB=0°,
∴∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB.
③当动点P在射线BA的左侧时,如图5,结论是:∠PAC=∠APB+∠PBD,
理由是:∵AC∥BD,
∴∠PMC=∠PBD,
∵∠PAC=∠APB+∠PMC,
∴∠PAC=∠APB+∠PBD.
20.(1)证明:∵∠A=90°,∠C=50°,BD平分∠ABC,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣90°﹣50°=40°,
∴∠ADB=∠CBD+∠C=∠ABC+∠C=×40°+50°=70°.
∵∠AME=∠C+∠MEC=50°+90°=140°,MF为∠AME的平分线,
∴∠AMF=∠AME=×140°=70°,
∴∠ADB=∠AMF=70°,
∴BD∥MF.
(2)M是AC延长线上的一点,过点M作ME⊥BC,交BC延长线于点E,过点M作∠AME平分线MF,交BA延长线于点F.
判断BD⊥MF.
证明:延长BD,交MF于点G.
∵在Rt△ABC和Rt△CMF中,∠BAC=∠CEM,∠BCA=∠MCE,
∴∠ABC=∠CME.
又∵BD、MF分别为∠ABC和∠CME的平分线,
∴∠FBG=∠AMF.
又∵∠AMF+∠AFM=90°,
∴∠FBG+∠AFM=90°,
∴∠BGF=90°,
∴BD⊥MF.
21.解:(1)如图所示:△DEF即为所求;
(2)△DEF的面积为:×2×3=3.
22.解:(1)设∠H的4系补周角的度数为x°,根据新定义得,120+4x=360,
解得,x=60,
∠H的4系补周角的度数为60°,
故答案为60;
(2)①过E作EF∥AB,如图1,
∴∠B=∠BEF,
∵AB∥CD,
∴EF∥CD,∠D=60°,
∴∠D=∠DEF=60°,
∵∠B+60°=∠BEF+∠DEF,
即∠B+60°=∠BED,
∵∠B是∠BED的3系补周角,
∴∠BED=360°﹣3∠B,
∴∠B+60°=360°﹣3∠B,
∴∠B=75°;
②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n
