第十章 §10.3 频率与概率 课时练(含答案)
文档属性
| 名称 | 第十章 §10.3 频率与概率 课时练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 114.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-02 17:20:30 | ||
图片预览



文档简介
§10.3 频率与概率
1.气象台预测“本市明天降雨的概率是90%”,对预测的正确理解是( )
A.本市明天将有90%的地区降雨
B.本市明天将有90%的时间降雨
C.明天出行不带雨具肯定会淋雨
D.明天出行不带雨具可能会淋雨
2.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品.若用C表示抽到次品这一事件,则对C这一事件发生的说法正确的是( )
A.概率为
B.频率为
C.概率接近
D.每抽10台电视机,必有1台次品
3.(多选)小明将一枚质地均匀的正方体骰子连续抛掷了10次,每次朝上的点数都是6,则下列说法正确的是( )
A.朝上的点数是6的概率和频率均为1
B.若抛掷10 000次,则朝上的点数是6的频率约为
C.抛掷第11次,朝上的点数一定不是6
D.抛掷6 000次,朝上的点数为6的次数大约为1 000次
4.一个盒子中有若干白色围棋子,为了估计其中围棋子的数目,小明将100颗黑色围棋子放入其中,充分搅拌后随机抽出了20颗,数得其中有5颗黑色围棋子,根据这些信息可以估计白色围棋子的数目为( )
A.200颗 B.300颗
C.400颗 D.500颗
5.某种心脏手术,成功率为0.6,现采用随机模拟方法估计“3例心脏手术全部成功”的概率:先利用计算器或计算机产生0~9之间的整数随机数,由于成功率是0.6,我们用0,1,2,3表示手术不成功,4,5,6,7,8,9表示手术成功;再以每3个随机数为一组,作为3例手术的结果,经随机模拟产生如下10组随机数:
812,832,569,683,271,989,730,537,925,907
由此估计“3例心脏手术全部成功”的概率为( )
A.0.2 B.0.3 C.0.4 D.0.5
6.(多选)某篮球运动员在最近几次参加的比赛中的投篮情况如表:
投篮次数 投中两分球的次数 投中三分球的次数
100 55 18
记该篮球运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55 B.P(B)=0.18
C.P(C)=0.27 D.P(B+C)=0.55
7.在用随机数(整数)模拟“有4个男生和5个女生,从中抽选4个,被抽选的4个中有2个男生、2个女生”的概率时,可让计算机产生1~9的随机整数,并且1~4代表男生,用5~9代表女生.因为是选出4个,所以每4个随机数作为一组.若得到的一组随机数为“4678”,则它代表的含义是______________________________.
8.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有50个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在30%和40%,则口袋中白色球的个数可能是______.
9.有一个转盘游戏,转盘被平均分成10等分(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下三种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍数”或“不是4的整数倍数”;
C.猜“是大于4的数”或“不是大于4的数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方案,并且怎样猜?为什么?
(2)为了保证游戏的公平性,你认为应制定哪种猜数方案?为什么?
(3)请你设计一种其他的猜数方案 ,并保证游戏的公平性.
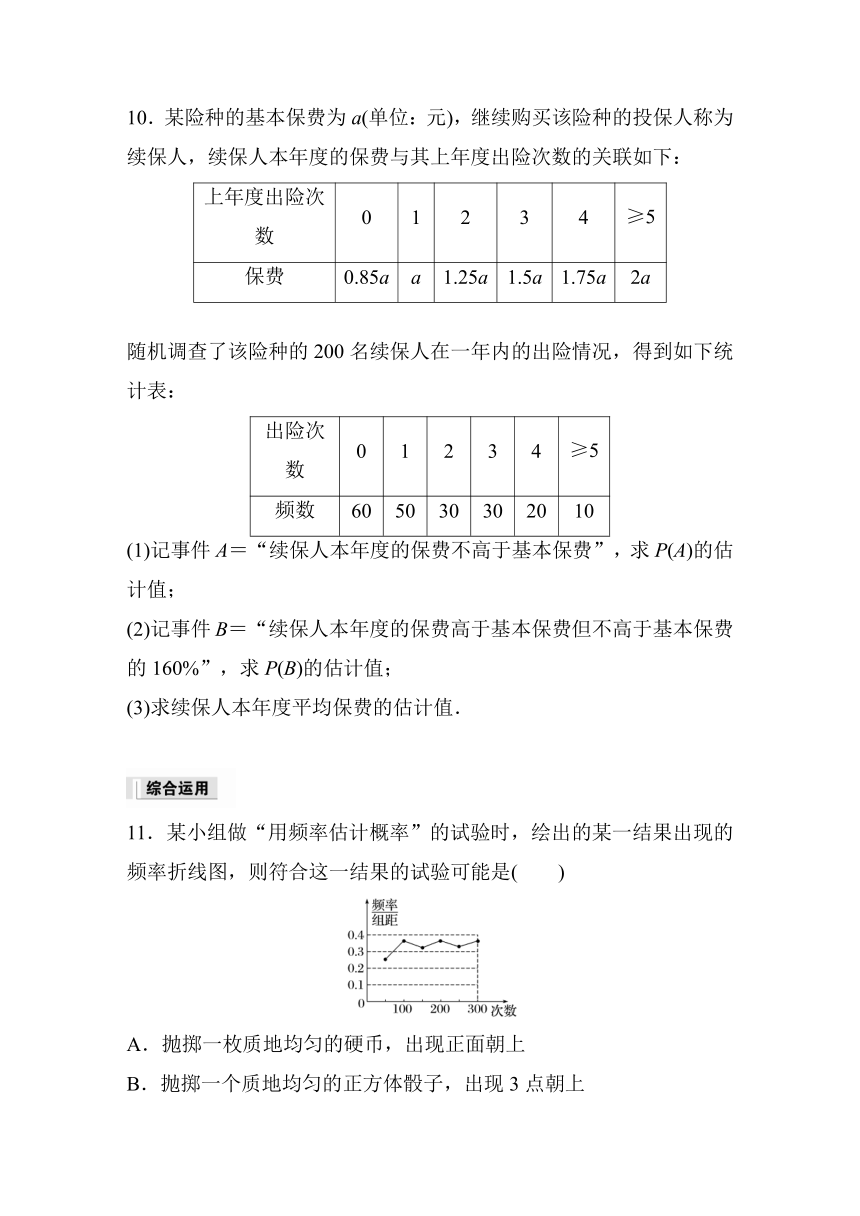
10.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 0 1 2 3 4 ≥5
保费 0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 0 1 2 3 4 ≥5
频数 60 50 30 30 20 10
(1)记事件A=“续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记事件B=“续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
11.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛掷一枚质地均匀的硬币,出现正面朝上
B.抛掷一个质地均匀的正方体骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任意抽取一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
12.某市交警部门在调查一起车祸的过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有两家出租车公司,其中甲公司有100辆桑塔纳出租车,3 000辆帕萨特出租车,乙公司有3 000辆桑塔纳出租车,100辆帕萨特出租车,交警部门应先调查哪个公司的车辆较合理( )
A.甲公司 B.乙公司
C.甲或乙公司均可 D.以上都对
13.(多选)某评分网站是将用户评价的一到五星转化为0~10的分值(一星2分,二星4分,三星6分,依此类推),以得分总和除以评分的用户人数所得的分值作为最终评分.某影片的评分情况如图,假如参与评价的观众中有97.6%的评价不低于二星,则下列说法正确的是( )
A.m的值是32.0%
B.随机抽取100名观众,则一定有24人评价五星
C.随机抽取一名观众,其评价是三星或五星的概率约为0.56
D.若从已作评价的观众中随机抽取3人,则事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件
14.通过模拟试验产生了20组随机数:
6830 3013 7055 7430 7740 4422 7884
2604 3346 0952 6807 9706 5774 5725
6576 5929 9768 6071 9138 6754
如果恰好有三个数在1,2,3,4,5,6中,表示恰好有三次击中目标,则四次射击中恰好有三次击中目标的概率约为________.
15.独立地重复一个随机试验n(n∈N,n≥1)次,设随机事件A发生的频率为f(n),随机事件A发生的概率为P,有如下两个判断:①如果集合{f(n)|n∈N,n≥1}中只含有一个元素,则P=1;②集合{f(n)|n∈N,n≥1}不可能只含有两个元素,其中( )
A.①正确,②正确 B.①错误,②正确
C.①正确,②错误 D.①错误,②错误
16.某控制器中有一个易损部件,现统计了30个该部件的使用寿命,结果如下(单位:小时):
710 721 603 615 760 742 841 591 590 721
718 750 760 713 709 681 736 654 722 732
722 715 726 699 755 751 709 733 705 700
(1)估计该部件的使用寿命达到一个月的概率(一个月按30天计算);
(2)为了保证该控制器能稳定工作,将n个同样的部件连接在一起组成集成块(如图),每一个部件是否能正常工作互不影响.对比n=2和n=3,哪个能保证集成块使用寿命达到一个月的概率超过0.8
§10.3 频率与概率
1.D 2.B 3.BD 4.B 5.A
6.ABC [依题意,P(A)==0.55,P(B)==0.18,显然事件A,B互斥,
P(C)=1-P(A+B)=1-P(A)-P(B)=0.27,
事件B,C互斥,则P(B+C)=P(B)+P(C)=0.45,故选项A,B,C都正确,选项D不正确.]
7.选出的4人中有1个男生、3个女生
8.15
9.解 (1)如题图,方案A中“是奇数”或“是偶数”的概率均为=0.5;方案B中“不是4的整数倍数”的概率为=0.8,“是4的整数倍数”的概率为=0.2;方案C中“是大于4的数”的概率为=0.6,“不是大于4的数”的概率为=0.4.乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”.
(2)为了保证游戏的公平性,应当选择方案A.因为方案A猜“是奇数”或“是偶数”的概率均为0.5,从而保证了该游戏是公平的.
(3)可以设计为:猜“是大于5的数”或“不是大于5的数”,此方案也可以保证游戏的公平性.
10.解 (1)事件A发生当且仅当一年内出险次数小于2,由所给数据知,一年内出险次数小于2的频率为=0.55,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4,由所给数据知,一年内出险次数大于1且小于4的频率为=0.3,故P(B)的估计值为0.3.
(3)由所给数据得
保费 0.85a a 1.25a 1.5a 1.75a 2a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为
0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.
因此,续保人本年度平均保费的估计值为1.192 5a.
11.D
12.B [由于甲公司桑塔纳的比例为=,乙公司桑塔纳的比例为=,
可知肇事车在乙公司的可能性大些,交警部门先调查乙公司较合理.]
13.ACD [对于A选项,参与评价的观众中有97.6%的评价不低于二星,则24.0%+32.9%+m+8.7%=97.6%,所以m=32.0%,故A正确;对于B选项,随机抽取100名观众,可能有100×24.0%=24(人)评价五星,但不是一定的,故B错误;对于C选项,由A选项知,评价是三星或五星的概率约为32.0%+24.0%=56.0%,故C正确;对于D选项,根据互斥事件和对立事件的定义可知,事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件,故D正确.]
14.0.25
解析 表示三次击中目标分别是3013,2604,5725,6576,6754,共5组数,而随机数总共20组,所以所求的概率约为=0.25.
15.B [①如果集合{f(n)|n∈N,n≥1}中只含有一个元素,而试验的频率只有一个值,事件A为必然事件或不可能事件,P=0或P=1,故①错误;
②频率随着试验次数的变化而变化,则集合{f(n)|n∈N,n≥1}不可能只含有两个元素,故②正确.]
16.解 (1)一天24小时,一个月30×24=720(小时),样本中满足使用寿命在720小时及以上的部件有15个,所以所求概率的估计值为=.
(2)要保证集成块使用寿命达到一个月,即要保证集成块中至少有一个部件的使用寿命达到一个月.记A表示一个部件的使用寿命达到一个月,a表示一个部件的使用寿命不能达到一个月.
当n=2时,
P1=1-×==0.75<0.8;
当n=3时,
P2=1-××=>0.8.
综上,当n=3时,满足要求.
1.气象台预测“本市明天降雨的概率是90%”,对预测的正确理解是( )
A.本市明天将有90%的地区降雨
B.本市明天将有90%的时间降雨
C.明天出行不带雨具肯定会淋雨
D.明天出行不带雨具可能会淋雨
2.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品.若用C表示抽到次品这一事件,则对C这一事件发生的说法正确的是( )
A.概率为
B.频率为
C.概率接近
D.每抽10台电视机,必有1台次品
3.(多选)小明将一枚质地均匀的正方体骰子连续抛掷了10次,每次朝上的点数都是6,则下列说法正确的是( )
A.朝上的点数是6的概率和频率均为1
B.若抛掷10 000次,则朝上的点数是6的频率约为
C.抛掷第11次,朝上的点数一定不是6
D.抛掷6 000次,朝上的点数为6的次数大约为1 000次
4.一个盒子中有若干白色围棋子,为了估计其中围棋子的数目,小明将100颗黑色围棋子放入其中,充分搅拌后随机抽出了20颗,数得其中有5颗黑色围棋子,根据这些信息可以估计白色围棋子的数目为( )
A.200颗 B.300颗
C.400颗 D.500颗
5.某种心脏手术,成功率为0.6,现采用随机模拟方法估计“3例心脏手术全部成功”的概率:先利用计算器或计算机产生0~9之间的整数随机数,由于成功率是0.6,我们用0,1,2,3表示手术不成功,4,5,6,7,8,9表示手术成功;再以每3个随机数为一组,作为3例手术的结果,经随机模拟产生如下10组随机数:
812,832,569,683,271,989,730,537,925,907
由此估计“3例心脏手术全部成功”的概率为( )
A.0.2 B.0.3 C.0.4 D.0.5
6.(多选)某篮球运动员在最近几次参加的比赛中的投篮情况如表:
投篮次数 投中两分球的次数 投中三分球的次数
100 55 18
记该篮球运动员在一次投篮中,投中两分球为事件A,投中三分球为事件B,没投中为事件C,用频率估计概率的方法,得到的下述结论中,正确的是( )
A.P(A)=0.55 B.P(B)=0.18
C.P(C)=0.27 D.P(B+C)=0.55
7.在用随机数(整数)模拟“有4个男生和5个女生,从中抽选4个,被抽选的4个中有2个男生、2个女生”的概率时,可让计算机产生1~9的随机整数,并且1~4代表男生,用5~9代表女生.因为是选出4个,所以每4个随机数作为一组.若得到的一组随机数为“4678”,则它代表的含义是______________________________.
8.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有50个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在30%和40%,则口袋中白色球的个数可能是______.
9.有一个转盘游戏,转盘被平均分成10等分(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下三种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍数”或“不是4的整数倍数”;
C.猜“是大于4的数”或“不是大于4的数”.
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方案,并且怎样猜?为什么?
(2)为了保证游戏的公平性,你认为应制定哪种猜数方案?为什么?
(3)请你设计一种其他的猜数方案 ,并保证游戏的公平性.
10.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 0 1 2 3 4 ≥5
保费 0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 0 1 2 3 4 ≥5
频数 60 50 30 30 20 10
(1)记事件A=“续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记事件B=“续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
11.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛掷一枚质地均匀的硬币,出现正面朝上
B.抛掷一个质地均匀的正方体骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任意抽取一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
12.某市交警部门在调查一起车祸的过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有两家出租车公司,其中甲公司有100辆桑塔纳出租车,3 000辆帕萨特出租车,乙公司有3 000辆桑塔纳出租车,100辆帕萨特出租车,交警部门应先调查哪个公司的车辆较合理( )
A.甲公司 B.乙公司
C.甲或乙公司均可 D.以上都对
13.(多选)某评分网站是将用户评价的一到五星转化为0~10的分值(一星2分,二星4分,三星6分,依此类推),以得分总和除以评分的用户人数所得的分值作为最终评分.某影片的评分情况如图,假如参与评价的观众中有97.6%的评价不低于二星,则下列说法正确的是( )
A.m的值是32.0%
B.随机抽取100名观众,则一定有24人评价五星
C.随机抽取一名观众,其评价是三星或五星的概率约为0.56
D.若从已作评价的观众中随机抽取3人,则事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件
14.通过模拟试验产生了20组随机数:
6830 3013 7055 7430 7740 4422 7884
2604 3346 0952 6807 9706 5774 5725
6576 5929 9768 6071 9138 6754
如果恰好有三个数在1,2,3,4,5,6中,表示恰好有三次击中目标,则四次射击中恰好有三次击中目标的概率约为________.
15.独立地重复一个随机试验n(n∈N,n≥1)次,设随机事件A发生的频率为f(n),随机事件A发生的概率为P,有如下两个判断:①如果集合{f(n)|n∈N,n≥1}中只含有一个元素,则P=1;②集合{f(n)|n∈N,n≥1}不可能只含有两个元素,其中( )
A.①正确,②正确 B.①错误,②正确
C.①正确,②错误 D.①错误,②错误
16.某控制器中有一个易损部件,现统计了30个该部件的使用寿命,结果如下(单位:小时):
710 721 603 615 760 742 841 591 590 721
718 750 760 713 709 681 736 654 722 732
722 715 726 699 755 751 709 733 705 700
(1)估计该部件的使用寿命达到一个月的概率(一个月按30天计算);
(2)为了保证该控制器能稳定工作,将n个同样的部件连接在一起组成集成块(如图),每一个部件是否能正常工作互不影响.对比n=2和n=3,哪个能保证集成块使用寿命达到一个月的概率超过0.8
§10.3 频率与概率
1.D 2.B 3.BD 4.B 5.A
6.ABC [依题意,P(A)==0.55,P(B)==0.18,显然事件A,B互斥,
P(C)=1-P(A+B)=1-P(A)-P(B)=0.27,
事件B,C互斥,则P(B+C)=P(B)+P(C)=0.45,故选项A,B,C都正确,选项D不正确.]
7.选出的4人中有1个男生、3个女生
8.15
9.解 (1)如题图,方案A中“是奇数”或“是偶数”的概率均为=0.5;方案B中“不是4的整数倍数”的概率为=0.8,“是4的整数倍数”的概率为=0.2;方案C中“是大于4的数”的概率为=0.6,“不是大于4的数”的概率为=0.4.乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”.
(2)为了保证游戏的公平性,应当选择方案A.因为方案A猜“是奇数”或“是偶数”的概率均为0.5,从而保证了该游戏是公平的.
(3)可以设计为:猜“是大于5的数”或“不是大于5的数”,此方案也可以保证游戏的公平性.
10.解 (1)事件A发生当且仅当一年内出险次数小于2,由所给数据知,一年内出险次数小于2的频率为=0.55,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4,由所给数据知,一年内出险次数大于1且小于4的频率为=0.3,故P(B)的估计值为0.3.
(3)由所给数据得
保费 0.85a a 1.25a 1.5a 1.75a 2a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为
0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.
因此,续保人本年度平均保费的估计值为1.192 5a.
11.D
12.B [由于甲公司桑塔纳的比例为=,乙公司桑塔纳的比例为=,
可知肇事车在乙公司的可能性大些,交警部门先调查乙公司较合理.]
13.ACD [对于A选项,参与评价的观众中有97.6%的评价不低于二星,则24.0%+32.9%+m+8.7%=97.6%,所以m=32.0%,故A正确;对于B选项,随机抽取100名观众,可能有100×24.0%=24(人)评价五星,但不是一定的,故B错误;对于C选项,由A选项知,评价是三星或五星的概率约为32.0%+24.0%=56.0%,故C正确;对于D选项,根据互斥事件和对立事件的定义可知,事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件,故D正确.]
14.0.25
解析 表示三次击中目标分别是3013,2604,5725,6576,6754,共5组数,而随机数总共20组,所以所求的概率约为=0.25.
15.B [①如果集合{f(n)|n∈N,n≥1}中只含有一个元素,而试验的频率只有一个值,事件A为必然事件或不可能事件,P=0或P=1,故①错误;
②频率随着试验次数的变化而变化,则集合{f(n)|n∈N,n≥1}不可能只含有两个元素,故②正确.]
16.解 (1)一天24小时,一个月30×24=720(小时),样本中满足使用寿命在720小时及以上的部件有15个,所以所求概率的估计值为=.
(2)要保证集成块使用寿命达到一个月,即要保证集成块中至少有一个部件的使用寿命达到一个月.记A表示一个部件的使用寿命达到一个月,a表示一个部件的使用寿命不能达到一个月.
当n=2时,
P1=1-×==0.75<0.8;
当n=3时,
P2=1-××=>0.8.
综上,当n=3时,满足要求.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
