曲边梯形的面积(教案)
图片预览

文档简介
曲边梯形的面积(教案)
杭州市源清中学 徐骋
【教学目标】
1、知识与技能目标:
通过问题情景,经历求曲面梯形的形成过程,了解定积分概念的实际背景。理解求曲面梯形的一般步骤。
2、过程与方法目标:
通过问题的探究体会以直代曲、以不变代变及无限逼近的思想。通过类比体会从具体到抽象、从特殊到一般的数学思想方法。
3、情感、态度与价值观目标:
体验和认同“有限和无限对立统一”的辩证观点,接受用运动变化的辩证唯物主义思想处理数学问题的积极态度。
【教学重点】
求一般曲面梯形面积的方法。
【教学难点】
对以直代曲、无限逼近思想的理解。
【教学准备】
多媒体电脑、课件等。
【教学过程】
教学环节 教学内容 学生活动 教师活动
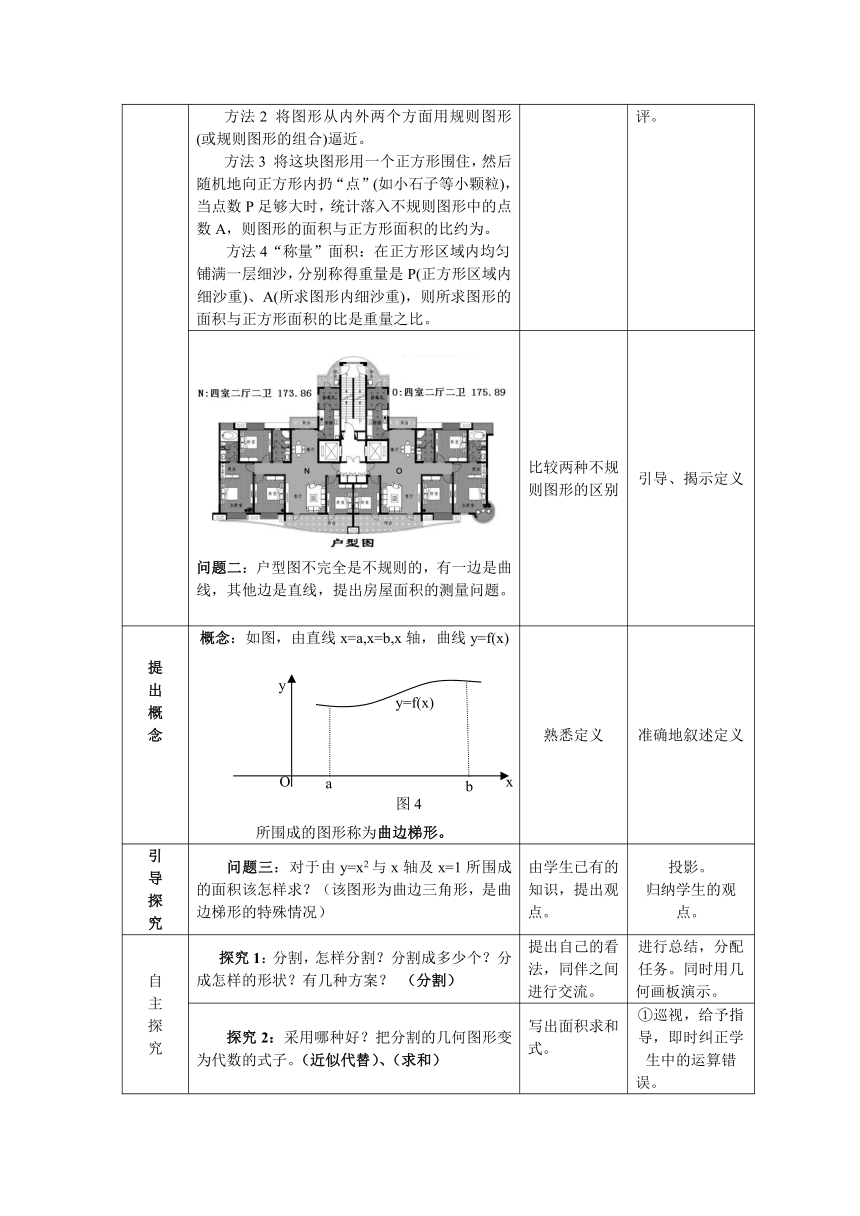
创设情景 问题一:我们在小学、初中就学习过求平面图形面积的问题。有的是规则的平面图形,但现实生活中更多的是不规则的平面图形。对于不规则的图形我们该如何求面积?比如浙江省的国土面积。此问题在学生九年级中已有涉及,在九年级时学生了解过以下求不规则面积的方法:方法1 将图形放在坐标纸上,也即将图形分割,看它有多少个“单位面积”。。方法2 将图形从内外两个方面用规则图形(或规则图形的组合)逼近。方法3 将这块图形用一个正方形围住,然后随机地向正方形内扔“点”(如小石子等小颗粒),当点数P足够大时,统计落入不规则图形中的点数A,则图形的面积与正方形面积的比约为。方法4“称量”面积:在正方形区域内均匀铺满一层细沙,分别称得重量是P(正方形区域内细沙重)、A(所求图形内细沙重),则所求图形的面积与正方形面积的比是重量之比。 回顾初中所学内容。 讲评:其中方法1、2蕴含积分的基本思想,方法3用随机模拟的方法,称为“蒙特卡罗方法”,方法4是伽利略测量摆线与直线围成的面积是所用的方法。根据学生的程度选择性的讲评。
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,提出房屋面积的测量问题。 比较两种不规则图形的区别 引导、揭示定义
提出概念 概念:如图,由直线x=a,x=b,x轴,曲线y=f(x)所围成的图形称为曲边梯形。 熟悉定义 准确地叙述定义
引导探究 问题三:对于由y=x2与x轴及x=1所围成的面积该怎样求?(该图形为曲边三角形,是曲边梯形的特殊情况) 由学生已有的知识,提出观点。 投影。归纳学生的观点。
自主探究 探究1:分割,怎样分割?分割成多少个?分成怎样的形状?有几种方案? (分割) 提出自己的看法,同伴之间进行交流。 进行总结,分配任务。同时用几何画板演示。
探究2:采用哪种好?把分割的几何图形变为代数的式子。(近似代替)、(求和) 写出面积求和式。 ①巡视,给予指导,即时纠正学生中的运算错误。②及时实物投影。③比较三种求和式的优劣,规定近似代替的原则。
探究3:如何用数学的形式表达分割的几何图形越来越多? (取极限) 写出分割无限多时,相应的数学含义。 及时实物投影。
探究4:采用过剩求和与不足求和所得到的结果一样,其意义是什么?(夹逼定理的意义) 发表自己的看法 总结,规范
问题四:如果不是在区间的两个端点取,而是在每一个区间中间取任意一点作为高,会有怎样的结果? 交流、提出看法 归纳、总结,讲评。
应用新知 练习1:求直线x=0,x=2,y=0与曲线y=x2所围成的曲边梯形的面积。练习2:求直线x=1,x=4,y=0与曲线y=x2所围成的曲边梯形的面积。 自主完成 巡视、实物展示
归纳总结 1、对于一般曲边梯形,如何求面积?2、求曲边梯形面积的方法步骤是什么?
作业布置 学案与作业
曲边梯形的面积(学案)
杭州市源清中学 徐骋
【学习目标】
1、理解“以直代曲”的意义;
2、理解求曲边梯形面积的四个步骤;
3、了解“近似代替”时取点的任意性。
【课堂程序】
问题一:我们在小学、初中就学面图形面积的问题。有的是规则的平面图形,但现实生活中更多的是不规则的平面图形。对于不规则的图形我们该如何求面积,比如浙江省的面积?
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,这样的面积又该怎样得出?
概念:如图,由直线x=a,x=b,x轴,曲线y=f(x)所围成的图形称为曲边梯形。
问题三:对于由y=x2与x轴及x=1所围成的面积该怎样求?
【知识应用】
1、求直线x=0,x=2,y=0与曲线y=x2所围成的曲边梯形的面积。
2、求直线x=1,x=4,y=0与曲线y=x2所围成的曲边梯形的面积。
【总结归纳】
1、对于一般曲边梯形,如何求面积?
2、求曲边梯形面积的方法步骤是什么?
【曲边梯形的面积 作业】
1、求由y=x2+1,和x=0,x=3,x轴围成的曲边梯形面积。
2、求由y=2x2+1,和x=1,x=3,x轴围成的曲边梯形面积。
图4
a
b
x
y
O
y=f(x)
图1
图4
a
b
x
y
O
y=f(x)
x
y
O
y=x2
图3
特别帮助:12+22+32+…+n2=n(n+1)(2n+1)
杭州市源清中学 徐骋
【教学目标】
1、知识与技能目标:
通过问题情景,经历求曲面梯形的形成过程,了解定积分概念的实际背景。理解求曲面梯形的一般步骤。
2、过程与方法目标:
通过问题的探究体会以直代曲、以不变代变及无限逼近的思想。通过类比体会从具体到抽象、从特殊到一般的数学思想方法。
3、情感、态度与价值观目标:
体验和认同“有限和无限对立统一”的辩证观点,接受用运动变化的辩证唯物主义思想处理数学问题的积极态度。
【教学重点】
求一般曲面梯形面积的方法。
【教学难点】
对以直代曲、无限逼近思想的理解。
【教学准备】
多媒体电脑、课件等。
【教学过程】
教学环节 教学内容 学生活动 教师活动
创设情景 问题一:我们在小学、初中就学习过求平面图形面积的问题。有的是规则的平面图形,但现实生活中更多的是不规则的平面图形。对于不规则的图形我们该如何求面积?比如浙江省的国土面积。此问题在学生九年级中已有涉及,在九年级时学生了解过以下求不规则面积的方法:方法1 将图形放在坐标纸上,也即将图形分割,看它有多少个“单位面积”。。方法2 将图形从内外两个方面用规则图形(或规则图形的组合)逼近。方法3 将这块图形用一个正方形围住,然后随机地向正方形内扔“点”(如小石子等小颗粒),当点数P足够大时,统计落入不规则图形中的点数A,则图形的面积与正方形面积的比约为。方法4“称量”面积:在正方形区域内均匀铺满一层细沙,分别称得重量是P(正方形区域内细沙重)、A(所求图形内细沙重),则所求图形的面积与正方形面积的比是重量之比。 回顾初中所学内容。 讲评:其中方法1、2蕴含积分的基本思想,方法3用随机模拟的方法,称为“蒙特卡罗方法”,方法4是伽利略测量摆线与直线围成的面积是所用的方法。根据学生的程度选择性的讲评。
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,提出房屋面积的测量问题。 比较两种不规则图形的区别 引导、揭示定义
提出概念 概念:如图,由直线x=a,x=b,x轴,曲线y=f(x)所围成的图形称为曲边梯形。 熟悉定义 准确地叙述定义
引导探究 问题三:对于由y=x2与x轴及x=1所围成的面积该怎样求?(该图形为曲边三角形,是曲边梯形的特殊情况) 由学生已有的知识,提出观点。 投影。归纳学生的观点。
自主探究 探究1:分割,怎样分割?分割成多少个?分成怎样的形状?有几种方案? (分割) 提出自己的看法,同伴之间进行交流。 进行总结,分配任务。同时用几何画板演示。
探究2:采用哪种好?把分割的几何图形变为代数的式子。(近似代替)、(求和) 写出面积求和式。 ①巡视,给予指导,即时纠正学生中的运算错误。②及时实物投影。③比较三种求和式的优劣,规定近似代替的原则。
探究3:如何用数学的形式表达分割的几何图形越来越多? (取极限) 写出分割无限多时,相应的数学含义。 及时实物投影。
探究4:采用过剩求和与不足求和所得到的结果一样,其意义是什么?(夹逼定理的意义) 发表自己的看法 总结,规范
问题四:如果不是在区间的两个端点取,而是在每一个区间中间取任意一点作为高,会有怎样的结果? 交流、提出看法 归纳、总结,讲评。
应用新知 练习1:求直线x=0,x=2,y=0与曲线y=x2所围成的曲边梯形的面积。练习2:求直线x=1,x=4,y=0与曲线y=x2所围成的曲边梯形的面积。 自主完成 巡视、实物展示
归纳总结 1、对于一般曲边梯形,如何求面积?2、求曲边梯形面积的方法步骤是什么?
作业布置 学案与作业
曲边梯形的面积(学案)
杭州市源清中学 徐骋
【学习目标】
1、理解“以直代曲”的意义;
2、理解求曲边梯形面积的四个步骤;
3、了解“近似代替”时取点的任意性。
【课堂程序】
问题一:我们在小学、初中就学面图形面积的问题。有的是规则的平面图形,但现实生活中更多的是不规则的平面图形。对于不规则的图形我们该如何求面积,比如浙江省的面积?
问题二:户型图不完全是不规则的,有一边是曲线,其他边是直线,这样的面积又该怎样得出?
概念:如图,由直线x=a,x=b,x轴,曲线y=f(x)所围成的图形称为曲边梯形。
问题三:对于由y=x2与x轴及x=1所围成的面积该怎样求?
【知识应用】
1、求直线x=0,x=2,y=0与曲线y=x2所围成的曲边梯形的面积。
2、求直线x=1,x=4,y=0与曲线y=x2所围成的曲边梯形的面积。
【总结归纳】
1、对于一般曲边梯形,如何求面积?
2、求曲边梯形面积的方法步骤是什么?
【曲边梯形的面积 作业】
1、求由y=x2+1,和x=0,x=3,x轴围成的曲边梯形面积。
2、求由y=2x2+1,和x=1,x=3,x轴围成的曲边梯形面积。
图4
a
b
x
y
O
y=f(x)
图1
图4
a
b
x
y
O
y=f(x)
x
y
O
y=x2
图3
特别帮助:12+22+32+…+n2=n(n+1)(2n+1)
