第九章 统计 章末检测试卷四(含答案)
文档属性
| 名称 | 第九章 统计 章末检测试卷四(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 478.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 00:00:00 | ||
图片预览




文档简介
第九章 统 计 章末检测试卷四
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了解某中学高一年级600名学生的身高情况,抽查了其中100名学生的身高进行统计分析.下列叙述错误的是( )
A.以上调查属于全面调查
B.每名学生的身高是总体的一个个体
C.100名学生的身高是总体的一个样本
D.600名学生的身高是总体
2.①一次数学考试中,某班有12人的成绩在100分以上,30人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关考试题目难度的情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层随机抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层随机抽样
D.分层随机抽样,分层随机抽样
3.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋中抽取60袋进行检验,利用随机数表抽样时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第7列开始向右读,则抽取检测的第5袋牛奶的编号是( )
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.199 B.175 C.507 D.12
4.某校高二年级有50人参加2023届“希望杯”数学竞赛,将他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
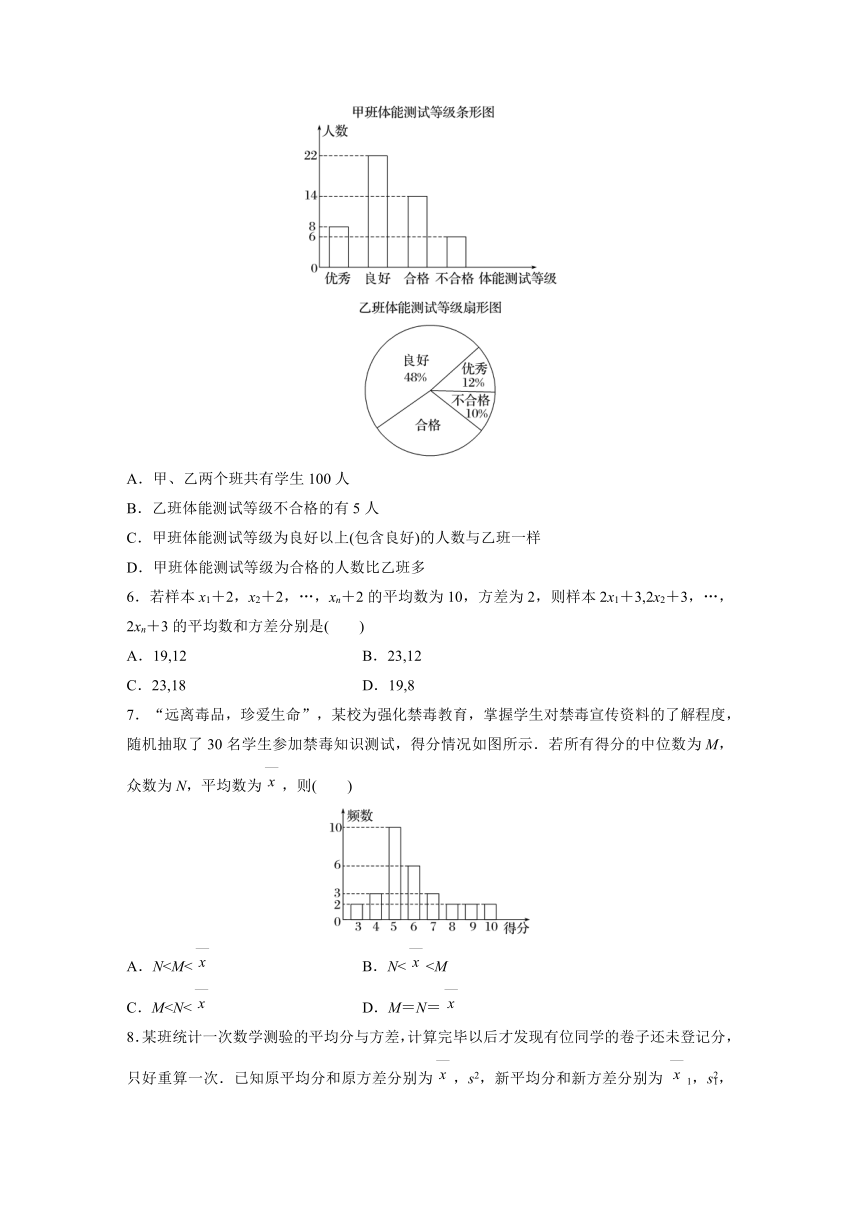
5.某校的体能测试结果分为优秀、良好、合格、不合格四个等级,已知甲、乙两个班的体能测试结果数据分别用条形图和扇形图描述,如图所示,若乙班的学生人数为50,则下列结论不正确的是( )
A.甲、乙两个班共有学生100人
B.乙班体能测试等级不合格的有5人
C.甲班体能测试等级为良好以上(包含良好)的人数与乙班一样
D.甲班体能测试等级为合格的人数比乙班多
6.若样本x1+2,x2+2,…,xn+2的平均数为10,方差为2,则样本2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
A.19,12 B.23,12
C.23,18 D.19,8
7.“远离毒品,珍爱生命”,某校为强化禁毒教育,掌握学生对禁毒宣传资料的了解程度,随机抽取了30名学生参加禁毒知识测试,得分情况如图所示.若所有得分的中位数为M,众数为N,平均数为,则( )
A.NC.M8.某班统计一次数学测验的平均分与方差,计算完毕以后才发现有位同学的卷子还未登记分,只好重算一次.已知原平均分和原方差分别为,s2,新平均分和新方差分别为1,s,若此同学的得分恰好为,则( )
A.=1,s2=s B.=1,s2C.=1,s2>s D.<1,s2=s
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.某地一年之内12个月的降水量分别为56,46,53,48,51,53,71,58,56,56,64,66,则关于该地区的月降水量,以下说法正确的是( )
A.20%分位数为51 B.75%分位数为61
C.中位数为56 D.平均数为57
10.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场的进球数是3.2,全年进球数的标准差为3;乙队平均每场的进球数是1.8,全年进球数的标准差为0.3.下列说法中正确的是( )
A.乙队的技术比甲队好
B.乙队比甲队发挥稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
11.下列叙述中,正确的是( )
A.若将一组数据的每个数都加上一个相同的正数x,则平均数和方差都会发生变化
B.某大学为了解在校本科生对参加某项社会实践活动的意向,采用按比例分配分层随机抽样的方法从该校四个年级的本科生中抽取一个容量为500的样本进行调查.已知该校一、二、三、四年级本科生人数之比为8∶5∶4∶k,若从四年级中抽取160名学生,则k=8
C.四名同学各掷骰子5次,分别记录每次骰子出现的点数,得到四组数据,若某组数据的平均数为2,方差为2.4,则这组数据一定没有出现6
D.一组数据按从小到大的顺序排列为1,4,4,x,7,8(其中x≠7),若该组数据的中位数是众数的倍,则该组数据的平均数为5
12.某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效问卷4 000份,根据所得信息制作了如图所示的频率分布直方图,则下列说法正确的是( )
A.a=0.028
B.在4 000份有效问卷中,短视频观众年龄在10~20岁的有1 320人
C.估计短视频观众的平均年龄为32岁
D.估计短视频观众年龄的75%分位数为39岁
三、填空题(本大题共4小题,每小题5分,共20分)
13.高一和高二两个年级的同学参加了数学竞赛,高一年级有450人,高二年级有350人,通过按比例分配的分层随机抽样的方法抽取了容量为160的样本,得到高一和高二两个年级的竞赛成绩的平均分分别为80分和90分,则高一、高二抽取的样本量分别为________;此次数学竞赛的平均分约为________分.
14.中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比是5∶7∶12∶10∶6,则这400名学生视力的众数约为________,中位数约为________.
15.A工厂年前加紧手套生产,设该工厂连续5天生产的手套数(单位:万只)依次为x1,x2,x3,x4,x5,若这组数据x1,x2,x3,x4,x5的方差为1.44,且x,x,x,x,x的平均数为4,则该工厂这5天平均每天生产手套________万只.
16.某校采用按比例分配的分层随机抽样的方法采集了高一、高二、高三年级学生的身高情况,部分调查数据如表:
项目 样本量 样本平均数 样本方差
高一 100 167 120
高二 100 170 150
高三 100 173 150
则总样本方差s2=________.
四、解答题(本大题共6小题,共70分)
17.(10分)我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万.为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布制作成如图所示的统计图.
(1)若采用按比例分配的分层随机抽样的方法从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上老人占全市户籍人口的百分比.
18.(12分)如图所示是总体的一个样本频率分布直方图,且在[15,18)内的频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33]内的频数.
19.在一次高二年级统一考试中,数学试卷有一道满分为10分的选做题,学生可以从A,B两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002,…,900.
(1)若采用随机数法抽样,并按照以下随机数表,以第一行第十三列的数字5为起点,从左向右依次读数,每次读取三位随机数,一行数读完之后接下一行左端.写出样本编号的中位数.
61 71 62 99 15 06 51 29 16 93
58 05 77 09 51 51 26 87 85 85
54 87 66 47 54 73 32 08 11 12
44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70
(2)若采用比例分配的分层随机抽样,按照学生选择A题目或B题目,将成绩分为两层,且样本中选择A题目的成绩有8个,平均数为7,方差为4;样本中选择B题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
20.(12分)已知A,B两家公司的员工月均工资(单位:万元)情况分别如图1,图2所示.
(1)以每组数据的区间中点值为代表,根据图1估计A公司员工月均工资的平均数、中位数,你认为用哪个数据更能反映该公司普通员工的工资水平?请说明理由;
(2)小明拟到A,B两家公司中的一家应聘,以公司普通员工的工资水平作为决策依据,他应该选哪个公司?
21.(12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)已知在这些数据中,质量指标值落在区间[75,105)内的产品的质量指标值的平均数为94,方差为40,所有这100件产品的质量指标值的平均数为100,方差为202,求质量指标值在区间[105,125]内的产品的质量指标值的方差.
22.(12分)中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管理,故因地得名宣纸,宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10 000刀(1刀=100张),该公司按照某种质量指标x给宣纸确定等级如表所示:
x的范围 (44,48]∪(52,56] (48,52] [0,44]∪(56,60]
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机抽取了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为15元,副牌宣纸的利润为8元,废品的利润为-20元.
(1)试估计该公司的年利润;
(2)市场上有一种售价为100万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命只有一年,且只能提高宣纸的质量,不能增加宣纸的年产量.据调查,这种机器生产的宣纸的质量指标x如表所示:
x的范围 (-2,+2) (-6,+6)
频率 0.682 7 0.954 5
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,该公司是否应该购买这种机器?请你为该公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
章末检测试卷四(第九章)
1.A 2.A 3.B 4.C 5.D 6.D
7.A
8.C [设这个班有n个同学,得分分别为a1,a2,…,ai,…,an,第i个同学的得分没登记(ai=),
第一次计算时总分为(n-1),
方差为s2=·[(a1-)2+…+(ai-1-)2+(ai+1-)2+…+(an-)2].
第二次计算时,平均数1==,
方差s=[(a1-)2+…+(ai-1-)2+(ai+1-)2+…+(an-)2+(-)2]=s2,故s2>s.]
9.ABC 10.BCD 11.BCD
12.CD [对于A,∵(0.015+0.033+a+0.011+0.011)×10=1,
∴a=0.03,故A错误;
对于B,由频率分布直方图,短视频观众年龄在10~20岁的对应频率为0.15,
∴短视频观众年龄在10~20岁的有4 000×0.15=600(人),故B错误;
对于C,平均年龄为
=(0.015×15+0.033×25+0.03×35+0.011×45+0.011×55)×10=32(岁),故C正确;
对于D,设75%分位数为x,
则0.015×10+0.033×10+(x-30)×0.03=0.75,
解得x=39,故D正确.]
13.90,70 84.375 14.4.7 4.75 15.1.6
16.146
解析 由题意知,总样本平均数为
=×167+×170+×173=170,
∴总样本方差为
s2=×[120+(167-170)2]+×[150+(170-170)2]+×[150+(173-170)2]
=146.
17.解 (1)数据整理如表所示:
健康情况 健康 基本健康 不健康尚能自理 不能自理
80岁及以上 20 45 20 15
80岁以下 200 225 50 25
从图表中知,
80岁及以上老人应抽取
8×=3(人).
80岁以下老人应抽取
8×=5(人).
(2)(20+45+20+15)÷600=,
×100%=2.75%,
估算该市80岁及以上老人占全市户籍人口的2.75%.
18.解 (1)由样本频率分布直方图得样本在[15,18)内的频率等于
×3=.
(2)∵样本在[15,18)内的频数为8,由(1)可知,样本容量为8÷=50.
(3)∵在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47,又在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
19.解 (1)根据题意,读取的编号依次是512,916(超界),935(超界),805,770,951(超界),512(重复),687,858,554,876,647,547,332.
将有效的编号由小到大排序,得332,512,547,554,647,687,770,805,858,876,
故样本编号的中位数为
=667.
(2)设样本中选择A题目的成绩的平均数为,方差为s2;
样本中选择B题目的成绩的平均数为,方差为t2,
则=7,s2=4,=8,t2=1,
所以样本的平均数为
+=×7+×8
=7.2,
方差为×[s2+(-7.2)2]+×[t2+(-7.2)2]
=×[4+(7-7.2)2]+×[1+(8-7.2)2]=3.56.
故该校900名学生的选做题得分的平均数约为7.2,方差约为3.56.
20.解 (1)A公司员工月均工资的平均数为
0.3×0.21+0.5×0.29+0.7×0.27+0.9×0.21+29×0.02
=1.166(万元).
由图1可知A公司员工月均工资在0.6万元以下的比例为
0.21+0.29=0.5,
所以A公司员工月均工资的中位数约为0.6万元.
用中位数更能反映该公司普通员工的工资水平,理由如下:
因为平均数受每一个数据的影响,越离群的数据对平均数的影响越大,该公司少数员工的月收入很高,在这种情况下平均数并不能较好地反映普通员工的收入水平,而中位数不受少数极端数据的影响,可以较好地反映普通员工的收入水平.
(2)B公司员工月均工资的平均数为
(0.3×0.375+0.5×0.75+0.7×2.75+0.9×1+1.1×0.125)×0.2=0.69(万元),
由图2知,B公司员工月均工资在0.6万元以下的频率为(0.375+0.75)×0.2=0.225,在0.8万元以下的频率为(0.375+0.75+2.75)×0.2=0.775.
设B公司员工月均工资的中位数为x万元,
则(x-0.6)×2.75=0.5-0.225,
解得x=0.7.
小明应选择B公司应聘,理由如下:
B公司员工工资数据较为集中,月均工资的平均数和中位数均能反映该公司普通员工的平均收入水平,B公司员工月均工资平均数为0.69,中位数为0.7,大于A公司员工月均工资的中位数0.6,所以以公司普通员工的工资水平作为决策依据,小明应该选B公司应聘.
21.解 (1)由题意可知,分组[75,85),[85,95),[95,105),[105,115),[115,125]对应的频率分别为0.06,0.26,0.38,0.22,0.08.
则频率分布直方图如图所示.
(2)质量指标值的样本平均数为
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为
s2=(100-80)2×0.06+(100-90)2×0.26+(100-100)2×0.38+(100-110)2×0.22+(100-120)2×0.08=104.
(3)由题意知,质量指标值落在区间[75,105)内的产品有70件,设质量指标值为x1,x2,…,x70,平均数为=94,方差为s=40,
则质量指标值落在区间[105,125]内的产品有30件,设质量指标值分别为y1,y2,…,y30,平均数为,方差为s,
则这100件产品的质量指标值的平均数为=100,方差为s=202,
则100=70+30,
所以=114,
所以s=300.
22.解 (1)由频率分布直方图得,一刀宣纸有正牌100×0.1×4=40(张),有副牌100×0.05×4×2=40(张),有废品100×0.025×4×2=20(张),
所以该公司一刀宣纸的利润的估计值为40×15+40×8+(-20)×20=520(元),
可以估计该公司的年利润为520万元.
(2)由频率分布直方图得,
=42×0.025×4+46×0.05×4+50×0.1×4+54×0.05×4+58×0.025×4=50.
由表格数据可得一刀宣纸中正牌的张数估计为
100×0.682 7=68.27,
废品的张数估计为100×(1-0.954 5)=4.55,
副牌的张数估计为100×(0.954 5-0.682 7)=27.18,
所以一刀宣纸的利润为68.27×12+27.18×5-4.55×20=864.14(元),
10 000刀宣纸的利润为10 000×864.14=8 641 400(元)=864.14(万元),
所以购买这种机器后该公司的利润为864.14-100=764.14(万元),
因为764.14>520,所以建议该公司购买这种机器.
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分)
1.为了解某中学高一年级600名学生的身高情况,抽查了其中100名学生的身高进行统计分析.下列叙述错误的是( )
A.以上调查属于全面调查
B.每名学生的身高是总体的一个个体
C.100名学生的身高是总体的一个样本
D.600名学生的身高是总体
2.①一次数学考试中,某班有12人的成绩在100分以上,30人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人了解有关考试题目难度的情况;②运动会的工作人员为参加4×100 m接力赛的6支队伍安排跑道.针对这两件事,恰当的抽样方法分别为( )
A.分层随机抽样,简单随机抽样
B.简单随机抽样,简单随机抽样
C.简单随机抽样,分层随机抽样
D.分层随机抽样,分层随机抽样
3.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋中抽取60袋进行检验,利用随机数表抽样时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第7列开始向右读,则抽取检测的第5袋牛奶的编号是( )
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.199 B.175 C.507 D.12
4.某校高二年级有50人参加2023届“希望杯”数学竞赛,将他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组 [60,70) [70,80) [80,90) [90,100]
频率 0.2 0.4 0.3 0.1
A.70 B.73 C.78 D.81.5
5.某校的体能测试结果分为优秀、良好、合格、不合格四个等级,已知甲、乙两个班的体能测试结果数据分别用条形图和扇形图描述,如图所示,若乙班的学生人数为50,则下列结论不正确的是( )
A.甲、乙两个班共有学生100人
B.乙班体能测试等级不合格的有5人
C.甲班体能测试等级为良好以上(包含良好)的人数与乙班一样
D.甲班体能测试等级为合格的人数比乙班多
6.若样本x1+2,x2+2,…,xn+2的平均数为10,方差为2,则样本2x1+3,2x2+3,…,2xn+3的平均数和方差分别是( )
A.19,12 B.23,12
C.23,18 D.19,8
7.“远离毒品,珍爱生命”,某校为强化禁毒教育,掌握学生对禁毒宣传资料的了解程度,随机抽取了30名学生参加禁毒知识测试,得分情况如图所示.若所有得分的中位数为M,众数为N,平均数为,则( )
A.N
A.=1,s2=s B.=1,s2
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.某地一年之内12个月的降水量分别为56,46,53,48,51,53,71,58,56,56,64,66,则关于该地区的月降水量,以下说法正确的是( )
A.20%分位数为51 B.75%分位数为61
C.中位数为56 D.平均数为57
10.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场的进球数是3.2,全年进球数的标准差为3;乙队平均每场的进球数是1.8,全年进球数的标准差为0.3.下列说法中正确的是( )
A.乙队的技术比甲队好
B.乙队比甲队发挥稳定
C.乙队几乎每场都进球
D.甲队的表现时好时坏
11.下列叙述中,正确的是( )
A.若将一组数据的每个数都加上一个相同的正数x,则平均数和方差都会发生变化
B.某大学为了解在校本科生对参加某项社会实践活动的意向,采用按比例分配分层随机抽样的方法从该校四个年级的本科生中抽取一个容量为500的样本进行调查.已知该校一、二、三、四年级本科生人数之比为8∶5∶4∶k,若从四年级中抽取160名学生,则k=8
C.四名同学各掷骰子5次,分别记录每次骰子出现的点数,得到四组数据,若某组数据的平均数为2,方差为2.4,则这组数据一定没有出现6
D.一组数据按从小到大的顺序排列为1,4,4,x,7,8(其中x≠7),若该组数据的中位数是众数的倍,则该组数据的平均数为5
12.某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效问卷4 000份,根据所得信息制作了如图所示的频率分布直方图,则下列说法正确的是( )
A.a=0.028
B.在4 000份有效问卷中,短视频观众年龄在10~20岁的有1 320人
C.估计短视频观众的平均年龄为32岁
D.估计短视频观众年龄的75%分位数为39岁
三、填空题(本大题共4小题,每小题5分,共20分)
13.高一和高二两个年级的同学参加了数学竞赛,高一年级有450人,高二年级有350人,通过按比例分配的分层随机抽样的方法抽取了容量为160的样本,得到高一和高二两个年级的竞赛成绩的平均分分别为80分和90分,则高一、高二抽取的样本量分别为________;此次数学竞赛的平均分约为________分.
14.中小学生的视力状况受到社会的广泛关注,某市有关部门从全市6万名高一学生中随机抽取了400名,对他们的视力状况进行一次调查统计,将所得到的有关数据绘制成频率分布直方图,如图所示.从左至右五个小组的频率之比是5∶7∶12∶10∶6,则这400名学生视力的众数约为________,中位数约为________.
15.A工厂年前加紧手套生产,设该工厂连续5天生产的手套数(单位:万只)依次为x1,x2,x3,x4,x5,若这组数据x1,x2,x3,x4,x5的方差为1.44,且x,x,x,x,x的平均数为4,则该工厂这5天平均每天生产手套________万只.
16.某校采用按比例分配的分层随机抽样的方法采集了高一、高二、高三年级学生的身高情况,部分调查数据如表:
项目 样本量 样本平均数 样本方差
高一 100 167 120
高二 100 170 150
高三 100 173 150
则总样本方差s2=________.
四、解答题(本大题共6小题,共70分)
17.(10分)我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万.为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布制作成如图所示的统计图.
(1)若采用按比例分配的分层随机抽样的方法从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上老人占全市户籍人口的百分比.
18.(12分)如图所示是总体的一个样本频率分布直方图,且在[15,18)内的频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小矩形面积为0.06,求在[18,33]内的频数.
19.在一次高二年级统一考试中,数学试卷有一道满分为10分的选做题,学生可以从A,B两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名学生的选做题成绩中随机抽取一个容量为10的样本,为此将900名学生的选做题的成绩随机编号为001,002,…,900.
(1)若采用随机数法抽样,并按照以下随机数表,以第一行第十三列的数字5为起点,从左向右依次读数,每次读取三位随机数,一行数读完之后接下一行左端.写出样本编号的中位数.
61 71 62 99 15 06 51 29 16 93
58 05 77 09 51 51 26 87 85 85
54 87 66 47 54 73 32 08 11 12
44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70
(2)若采用比例分配的分层随机抽样,按照学生选择A题目或B题目,将成绩分为两层,且样本中选择A题目的成绩有8个,平均数为7,方差为4;样本中选择B题目的成绩有2个,平均数为8,方差为1.试用样本估计该校900名学生的选做题得分的平均数与方差.
20.(12分)已知A,B两家公司的员工月均工资(单位:万元)情况分别如图1,图2所示.
(1)以每组数据的区间中点值为代表,根据图1估计A公司员工月均工资的平均数、中位数,你认为用哪个数据更能反映该公司普通员工的工资水平?请说明理由;
(2)小明拟到A,B两家公司中的一家应聘,以公司普通员工的工资水平作为决策依据,他应该选哪个公司?
21.(12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125]
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)已知在这些数据中,质量指标值落在区间[75,105)内的产品的质量指标值的平均数为94,方差为40,所有这100件产品的质量指标值的平均数为100,方差为202,求质量指标值在区间[105,125]内的产品的质量指标值的方差.
22.(12分)中国独有的文书工具,即笔、墨、纸、砚,有文房四宝之名,起源于南北朝时期.其中宣纸“始于唐代,产于泾县”,因唐代泾县隶属宣州管理,故因地得名宣纸,宣纸按质量等级分为:正牌(优等品)、副牌(合格品)、废品三等.某公司生产的宣纸为纯手工制作,年产宣纸10 000刀(1刀=100张),该公司按照某种质量指标x给宣纸确定等级如表所示:
x的范围 (44,48]∪(52,56] (48,52] [0,44]∪(56,60]
质量等级 副牌 正牌 废品
在该公司所生产的宣纸中随机抽取了一刀进行检验,得到频率分布直方图如图所示,已知每张正牌宣纸的利润为15元,副牌宣纸的利润为8元,废品的利润为-20元.
(1)试估计该公司的年利润;
(2)市场上有一种售价为100万元的机器可以改进宣纸的生产工艺,但这种机器的使用寿命只有一年,且只能提高宣纸的质量,不能增加宣纸的年产量.据调查,这种机器生产的宣纸的质量指标x如表所示:
x的范围 (-2,+2) (-6,+6)
频率 0.682 7 0.954 5
其中为质量指标x的平均值,但是由于人们对传统手工工艺的认可,改进后的正牌和副牌宣纸的利润都将下降3元/张,该公司是否应该购买这种机器?请你为该公司提出合理建议,并说明理由.(同一组的数据用该组区间的中点值作代表)
章末检测试卷四(第九章)
1.A 2.A 3.B 4.C 5.D 6.D
7.A
8.C [设这个班有n个同学,得分分别为a1,a2,…,ai,…,an,第i个同学的得分没登记(ai=),
第一次计算时总分为(n-1),
方差为s2=·[(a1-)2+…+(ai-1-)2+(ai+1-)2+…+(an-)2].
第二次计算时,平均数1==,
方差s=[(a1-)2+…+(ai-1-)2+(ai+1-)2+…+(an-)2+(-)2]=s2,故s2>s.]
9.ABC 10.BCD 11.BCD
12.CD [对于A,∵(0.015+0.033+a+0.011+0.011)×10=1,
∴a=0.03,故A错误;
对于B,由频率分布直方图,短视频观众年龄在10~20岁的对应频率为0.15,
∴短视频观众年龄在10~20岁的有4 000×0.15=600(人),故B错误;
对于C,平均年龄为
=(0.015×15+0.033×25+0.03×35+0.011×45+0.011×55)×10=32(岁),故C正确;
对于D,设75%分位数为x,
则0.015×10+0.033×10+(x-30)×0.03=0.75,
解得x=39,故D正确.]
13.90,70 84.375 14.4.7 4.75 15.1.6
16.146
解析 由题意知,总样本平均数为
=×167+×170+×173=170,
∴总样本方差为
s2=×[120+(167-170)2]+×[150+(170-170)2]+×[150+(173-170)2]
=146.
17.解 (1)数据整理如表所示:
健康情况 健康 基本健康 不健康尚能自理 不能自理
80岁及以上 20 45 20 15
80岁以下 200 225 50 25
从图表中知,
80岁及以上老人应抽取
8×=3(人).
80岁以下老人应抽取
8×=5(人).
(2)(20+45+20+15)÷600=,
×100%=2.75%,
估算该市80岁及以上老人占全市户籍人口的2.75%.
18.解 (1)由样本频率分布直方图得样本在[15,18)内的频率等于
×3=.
(2)∵样本在[15,18)内的频数为8,由(1)可知,样本容量为8÷=50.
(3)∵在[12,15)内的小矩形面积为0.06,故样本在[12,15)内的频率为0.06,故样本在[15,33)内的频数为50×(1-0.06)=47,又在[15,18)内的频数为8,故在[18,33)内的频数为47-8=39.
19.解 (1)根据题意,读取的编号依次是512,916(超界),935(超界),805,770,951(超界),512(重复),687,858,554,876,647,547,332.
将有效的编号由小到大排序,得332,512,547,554,647,687,770,805,858,876,
故样本编号的中位数为
=667.
(2)设样本中选择A题目的成绩的平均数为,方差为s2;
样本中选择B题目的成绩的平均数为,方差为t2,
则=7,s2=4,=8,t2=1,
所以样本的平均数为
+=×7+×8
=7.2,
方差为×[s2+(-7.2)2]+×[t2+(-7.2)2]
=×[4+(7-7.2)2]+×[1+(8-7.2)2]=3.56.
故该校900名学生的选做题得分的平均数约为7.2,方差约为3.56.
20.解 (1)A公司员工月均工资的平均数为
0.3×0.21+0.5×0.29+0.7×0.27+0.9×0.21+29×0.02
=1.166(万元).
由图1可知A公司员工月均工资在0.6万元以下的比例为
0.21+0.29=0.5,
所以A公司员工月均工资的中位数约为0.6万元.
用中位数更能反映该公司普通员工的工资水平,理由如下:
因为平均数受每一个数据的影响,越离群的数据对平均数的影响越大,该公司少数员工的月收入很高,在这种情况下平均数并不能较好地反映普通员工的收入水平,而中位数不受少数极端数据的影响,可以较好地反映普通员工的收入水平.
(2)B公司员工月均工资的平均数为
(0.3×0.375+0.5×0.75+0.7×2.75+0.9×1+1.1×0.125)×0.2=0.69(万元),
由图2知,B公司员工月均工资在0.6万元以下的频率为(0.375+0.75)×0.2=0.225,在0.8万元以下的频率为(0.375+0.75+2.75)×0.2=0.775.
设B公司员工月均工资的中位数为x万元,
则(x-0.6)×2.75=0.5-0.225,
解得x=0.7.
小明应选择B公司应聘,理由如下:
B公司员工工资数据较为集中,月均工资的平均数和中位数均能反映该公司普通员工的平均收入水平,B公司员工月均工资平均数为0.69,中位数为0.7,大于A公司员工月均工资的中位数0.6,所以以公司普通员工的工资水平作为决策依据,小明应该选B公司应聘.
21.解 (1)由题意可知,分组[75,85),[85,95),[95,105),[105,115),[115,125]对应的频率分别为0.06,0.26,0.38,0.22,0.08.
则频率分布直方图如图所示.
(2)质量指标值的样本平均数为
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为
s2=(100-80)2×0.06+(100-90)2×0.26+(100-100)2×0.38+(100-110)2×0.22+(100-120)2×0.08=104.
(3)由题意知,质量指标值落在区间[75,105)内的产品有70件,设质量指标值为x1,x2,…,x70,平均数为=94,方差为s=40,
则质量指标值落在区间[105,125]内的产品有30件,设质量指标值分别为y1,y2,…,y30,平均数为,方差为s,
则这100件产品的质量指标值的平均数为=100,方差为s=202,
则100=70+30,
所以=114,
所以s=300.
22.解 (1)由频率分布直方图得,一刀宣纸有正牌100×0.1×4=40(张),有副牌100×0.05×4×2=40(张),有废品100×0.025×4×2=20(张),
所以该公司一刀宣纸的利润的估计值为40×15+40×8+(-20)×20=520(元),
可以估计该公司的年利润为520万元.
(2)由频率分布直方图得,
=42×0.025×4+46×0.05×4+50×0.1×4+54×0.05×4+58×0.025×4=50.
由表格数据可得一刀宣纸中正牌的张数估计为
100×0.682 7=68.27,
废品的张数估计为100×(1-0.954 5)=4.55,
副牌的张数估计为100×(0.954 5-0.682 7)=27.18,
所以一刀宣纸的利润为68.27×12+27.18×5-4.55×20=864.14(元),
10 000刀宣纸的利润为10 000×864.14=8 641 400(元)=864.14(万元),
所以购买这种机器后该公司的利润为864.14-100=764.14(万元),
因为764.14>520,所以建议该公司购买这种机器.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
