4.1.1 相交与平行 课件(共30张PPT)
文档属性
| 名称 | 4.1.1 相交与平行 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
4.1 平面上两条直线的位置关系
4.1.1 相交与平行
1.了解相交与平行的概念及表示方法,会画平行线.
2.掌握平行公理及推论的内容,并初步了解几何推理过程.
3.在丰富的现实情境中,进一步了解两条直线的平行关系.
4.通过动手操作,培养学生参与活动和相互交流的意识,进而发展想象力和学习数学的兴趣,逐步培养学生的逻辑思维能力.
【教学重点】平行线的概念、平行线的画法、平行公理及推论.
【教学难点】平行公理的应用、平行线的画法.
观察下列图片,说一说直线与直线的位置关系.
情景导入
情境导入
生活中的平行线
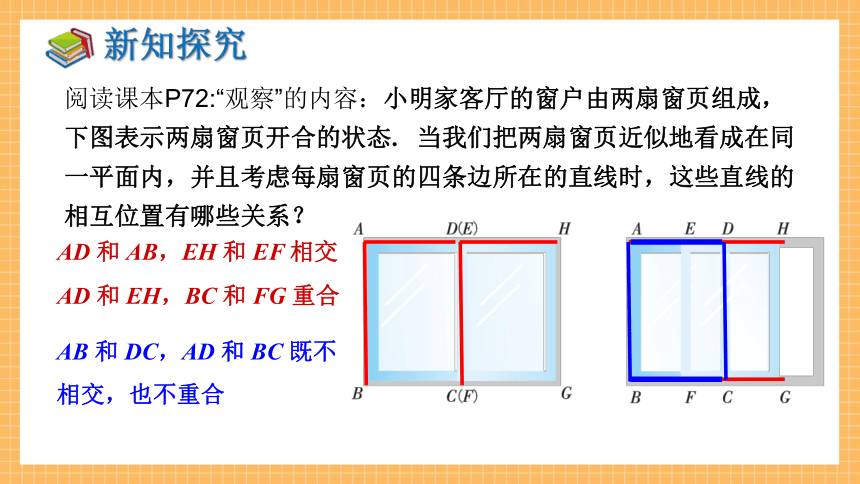
阅读课本P72:“观察”的内容:小明家客厅的窗户由两扇窗页组成,下图表示两扇窗页开合的状态. 当我们把两扇窗页近似地看成在同一平面内,并且考虑每扇窗页的四条边所在的直线时,这些直线的相互位置有哪些关系?
AD 和 AB,EH 和 EF 相交
AD 和 EH,BC 和 FG 重合
AB 和 DC,AD 和 BC 既不相交,也不重合
在同一平面内两条直线有什么位置关系呢?
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合.
今后如果没有特别说明,两条重合的直线只当做一条.
在同一平面内两条直线有什么位置关系呢?
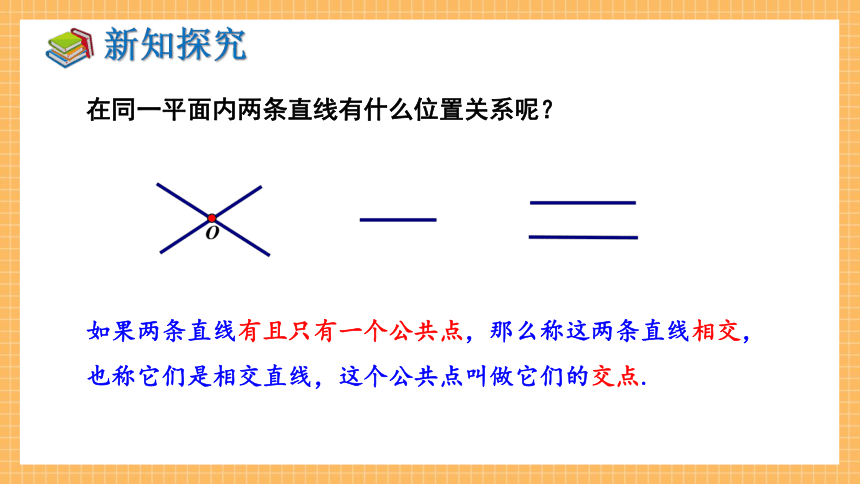
如果两条直线有且只有一个公共点,那么称这两条直线相交,也称它们是相交直线,这个公共点叫做它们的交点.
注意:
如果没有特别说明,两条重合的直线只当做一条.
两条直线有两个公共点,那么它们一定重合;两条直线有且只有一个公共点,那么称它们相交。
相交直线位置关系:正交(垂直)、斜交(不垂直)
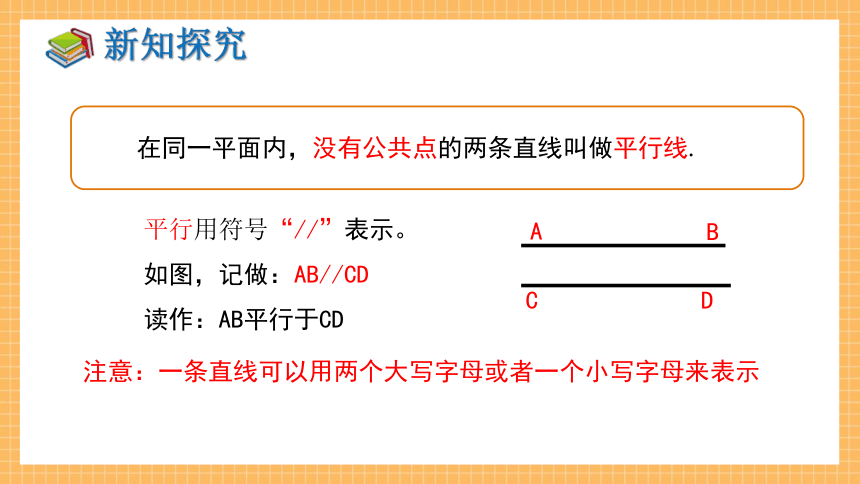
在同一平面内,没有公共点的两条直线叫做平行线.
平行用符号“//”表示。
如图,记做:AB//CD
读作:AB平行于CD
C
B
A
D
注意:一条直线可以用两个大写字母或者一个小写字母来表示
如何画平行线?
b
a
d
c
.
A
B
P
(1)放
(2)靠
(3)推
(4)画
平行线的画法:
你能过 P 点画几条直线与直线 a 平行?由此,你能得到什么结论?
过直线外一点有且只有一条直线与这条直线平行.
人们从长期的实践经验中抽象出如下基本事实:
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行, 这是不可能的. 所以 a∥c.
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
平行公理推论:
平行于同一直线的两条直线平行.
几何语言:
因为 a∥b,c∥b,
所以 a∥c (平行于同一条直线的两条直线互相平行).
平行公理
过直线外一点有且只有一条直线与这条直线平行.
平行公理推论
平行于同一条直线的两条直线平行.
1、判断:
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线;
(3)在同一平面内,不相交也不重合的两条射线一定平行;
(4)在同一平面内,不相交也不重合的两条直线一定平行;
(5)过一点有且只有一条直线与已知直线平行;
(6)两条没有公共点的直线叫做平行线。
错
错
错
对
错
错
2. 下列说法正确的是( )
A. 在同一平面内,不相交的两条射线是平行线
B. 在同一平面内,不相交的两条线段是平行线
C. 在同一平面内,两条不重合的直线的位置关系不相交就平行
D. 不相交的两条直线是平行线
C
3. 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
(A)a⊥b (B)a∥b
(C)a⊥b或a∥b (D)无法确定
【解析】选B.根据平行线的性质“平行于同一条直线的两条直线平行”得a∥b.
B
4. 下列说法正确的是( )
A. 一条直线的平行线有且只有一条
B. 经过一点有且只有一条直线与已知直线平行
C. 经过一点有两条直线与某一直线平行
D. 过直线外一点有且只有一条直线与已知直线平行
D
5、如图,已知AB//CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
证明:假设EF//CD
∵ AB//CD
根据平行于同一条直线的两条直线平行
∴AB//EF
这与EF与AB相交于点P矛盾
∴ EF与CD不平行
A
B
C
D
E
F
P
6. 下列推理正确的是( )
A. 因为 a∥d,b∥c,所以 c∥d
B. 因为 a∥c,b∥d,所以 c∥d
C. 因为 a∥b,a∥c,所以 b∥c
D. 因为 a∥b,c∥d,所以 a∥c
C
7、读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.
(1)
(2)
.
P
E
F
D
C
8. 完成下列推理,并在括号内注明理由.
(1)如图所示,因为 AB∥DE,BC∥DE(已知),
所以 A,B,C 三点 ; ( )
·
·
·
A
D
E
B
C
在同一条直线上
过直线外一点有且只有一条直线与这条直线平行
(2)如图所示,因为 AB∥CD,CD∥EF(已知),
所以____∥____ ( ).
C
A
B
D
E
F
AB
EF
平行于同一条直线的两条直线平行
9.一个长方体如图.
(1)和 AA1平行的棱有多少条?
(2)和 AB 平行的棱有多少条?
(3)和 AD 平行的棱有多少条?请分别表示出来.
解:(1)有 3 条,分别为:BB1 , CC1 , DD1.
(2)有 3 条,分别为:A1B1 , C1D1 , CD.
(3)有 3 条,分别为:A1D1 , B1C1 , BC.
通过本课时的学习,我们需要掌握:
1.在同一平面内没有公共点的两条直线叫做平行线.
2.平行线的表示.
3.平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
4.平行公理推论:平行于同一条直线的两条直线平行.
1. 习题4.1中第1、2题.
2.完成同步练习册中本课时的练习.
4.1 平面上两条直线的位置关系
4.1.1 相交与平行
1.了解相交与平行的概念及表示方法,会画平行线.
2.掌握平行公理及推论的内容,并初步了解几何推理过程.
3.在丰富的现实情境中,进一步了解两条直线的平行关系.
4.通过动手操作,培养学生参与活动和相互交流的意识,进而发展想象力和学习数学的兴趣,逐步培养学生的逻辑思维能力.
【教学重点】平行线的概念、平行线的画法、平行公理及推论.
【教学难点】平行公理的应用、平行线的画法.
观察下列图片,说一说直线与直线的位置关系.
情景导入
情境导入
生活中的平行线
阅读课本P72:“观察”的内容:小明家客厅的窗户由两扇窗页组成,下图表示两扇窗页开合的状态. 当我们把两扇窗页近似地看成在同一平面内,并且考虑每扇窗页的四条边所在的直线时,这些直线的相互位置有哪些关系?
AD 和 AB,EH 和 EF 相交
AD 和 EH,BC 和 FG 重合
AB 和 DC,AD 和 BC 既不相交,也不重合
在同一平面内两条直线有什么位置关系呢?
同一平面内的两条直线有三种位置关系: 相交、重合、既不相交也不重合.
今后如果没有特别说明,两条重合的直线只当做一条.
在同一平面内两条直线有什么位置关系呢?
如果两条直线有且只有一个公共点,那么称这两条直线相交,也称它们是相交直线,这个公共点叫做它们的交点.
注意:
如果没有特别说明,两条重合的直线只当做一条.
两条直线有两个公共点,那么它们一定重合;两条直线有且只有一个公共点,那么称它们相交。
相交直线位置关系:正交(垂直)、斜交(不垂直)
在同一平面内,没有公共点的两条直线叫做平行线.
平行用符号“//”表示。
如图,记做:AB//CD
读作:AB平行于CD
C
B
A
D
注意:一条直线可以用两个大写字母或者一个小写字母来表示
如何画平行线?
b
a
d
c
.
A
B
P
(1)放
(2)靠
(3)推
(4)画
平行线的画法:
你能过 P 点画几条直线与直线 a 平行?由此,你能得到什么结论?
过直线外一点有且只有一条直线与这条直线平行.
人们从长期的实践经验中抽象出如下基本事实:
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
若 a 与 c 不平行, 就会相交于某一点 P ,那么过点P 就有两条直线与 b 平行, 这是不可能的. 所以 a∥c.
如果直线 a 与 c 都和直线 b 平行,那么 a 与 c 平行吗?
平行公理推论:
平行于同一直线的两条直线平行.
几何语言:
因为 a∥b,c∥b,
所以 a∥c (平行于同一条直线的两条直线互相平行).
平行公理
过直线外一点有且只有一条直线与这条直线平行.
平行公理推论
平行于同一条直线的两条直线平行.
1、判断:
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线;
(3)在同一平面内,不相交也不重合的两条射线一定平行;
(4)在同一平面内,不相交也不重合的两条直线一定平行;
(5)过一点有且只有一条直线与已知直线平行;
(6)两条没有公共点的直线叫做平行线。
错
错
错
对
错
错
2. 下列说法正确的是( )
A. 在同一平面内,不相交的两条射线是平行线
B. 在同一平面内,不相交的两条线段是平行线
C. 在同一平面内,两条不重合的直线的位置关系不相交就平行
D. 不相交的两条直线是平行线
C
3. 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
(A)a⊥b (B)a∥b
(C)a⊥b或a∥b (D)无法确定
【解析】选B.根据平行线的性质“平行于同一条直线的两条直线平行”得a∥b.
B
4. 下列说法正确的是( )
A. 一条直线的平行线有且只有一条
B. 经过一点有且只有一条直线与已知直线平行
C. 经过一点有两条直线与某一直线平行
D. 过直线外一点有且只有一条直线与已知直线平行
D
5、如图,已知AB//CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
证明:假设EF//CD
∵ AB//CD
根据平行于同一条直线的两条直线平行
∴AB//EF
这与EF与AB相交于点P矛盾
∴ EF与CD不平行
A
B
C
D
E
F
P
6. 下列推理正确的是( )
A. 因为 a∥d,b∥c,所以 c∥d
B. 因为 a∥c,b∥d,所以 c∥d
C. 因为 a∥b,a∥c,所以 b∥c
D. 因为 a∥b,c∥d,所以 a∥c
C
7、读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.
(1)
(2)
.
P
E
F
D
C
8. 完成下列推理,并在括号内注明理由.
(1)如图所示,因为 AB∥DE,BC∥DE(已知),
所以 A,B,C 三点 ; ( )
·
·
·
A
D
E
B
C
在同一条直线上
过直线外一点有且只有一条直线与这条直线平行
(2)如图所示,因为 AB∥CD,CD∥EF(已知),
所以____∥____ ( ).
C
A
B
D
E
F
AB
EF
平行于同一条直线的两条直线平行
9.一个长方体如图.
(1)和 AA1平行的棱有多少条?
(2)和 AB 平行的棱有多少条?
(3)和 AD 平行的棱有多少条?请分别表示出来.
解:(1)有 3 条,分别为:BB1 , CC1 , DD1.
(2)有 3 条,分别为:A1B1 , C1D1 , CD.
(3)有 3 条,分别为:A1D1 , B1C1 , BC.
通过本课时的学习,我们需要掌握:
1.在同一平面内没有公共点的两条直线叫做平行线.
2.平行线的表示.
3.平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
4.平行公理推论:平行于同一条直线的两条直线平行.
1. 习题4.1中第1、2题.
2.完成同步练习册中本课时的练习.
