4.1.2 相交直线所成的角 课件(共41张PPT)
文档属性
| 名称 | 4.1.2 相交直线所成的角 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 15:36:41 | ||
图片预览






文档简介
(共41张PPT)
4.1 平面上两条直线的位置关系
4.1.2 相交直线所成的角
1.理解对顶角、同位角、内错角、同旁内角的概念.
2.结合图形识别同位角、内错角、同旁内角.
3.经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理的表达能力.
4.培养学生的空间想象能力和数学思维能力.
【教学重点】同位角、内错角、同旁内角的识别.
【教学难点】分析图形.
1.在同一平面内的两条直线有几种位置关系?
2.经过直线外一点怎样画出这条直线的平行线?
3.如果两条直线都与第三条直线平行,那么这两条直线互相平行,
即如果 a∥b,b∥c,那么 a∥c.
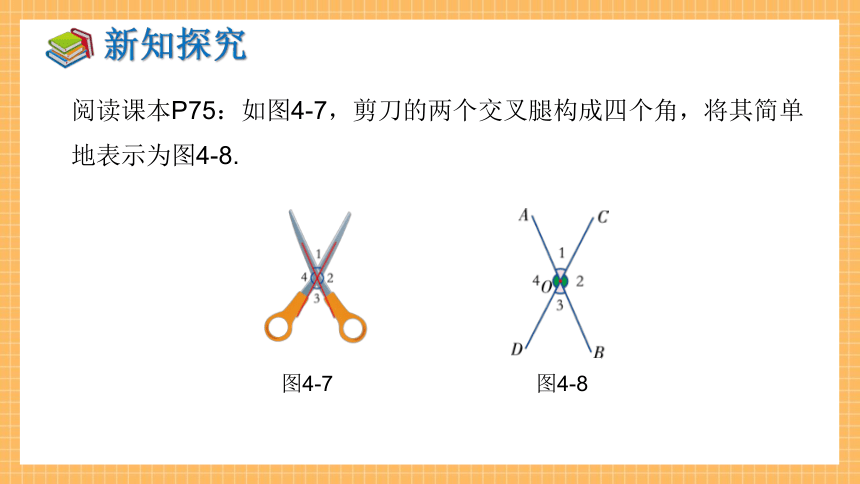
阅读课本P75:如图4-7,剪刀的两个交叉腿构成四个角,将其简单地表示为图4-8.
图4-7
图4-8
1
2
3
4
A
B
C
D
1
2
3
4
A
B
C
D
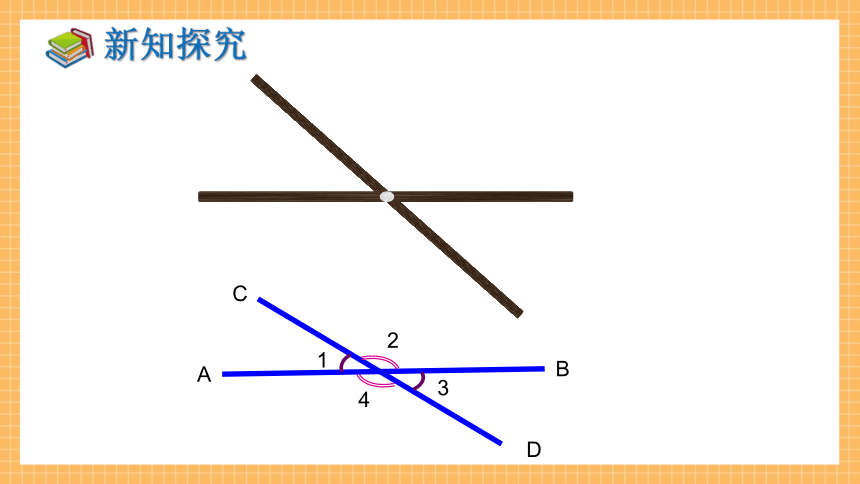
∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
发现
图中还有哪些角也是邻补角呢?
1
2
3
4
A
B
C
D
O
发现
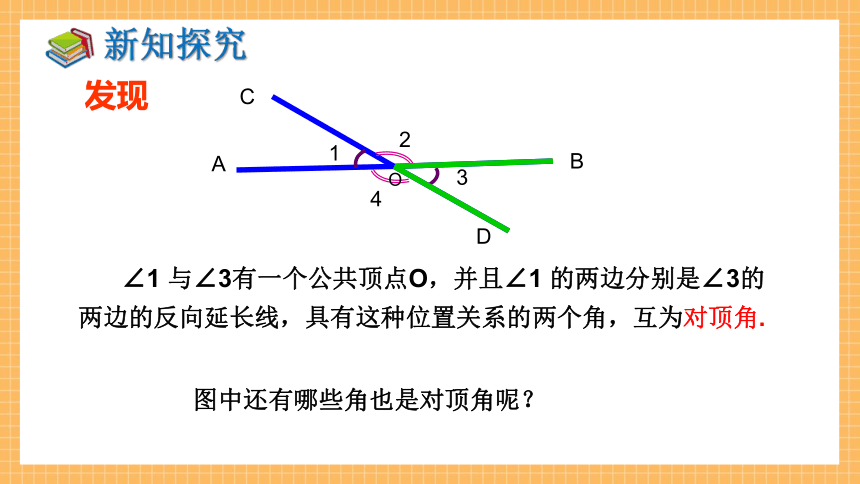
图中还有哪些角也是对顶角呢?
∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
A
B
C
D
1
3
4
2
O
A
B
C
D
1
3
4
2
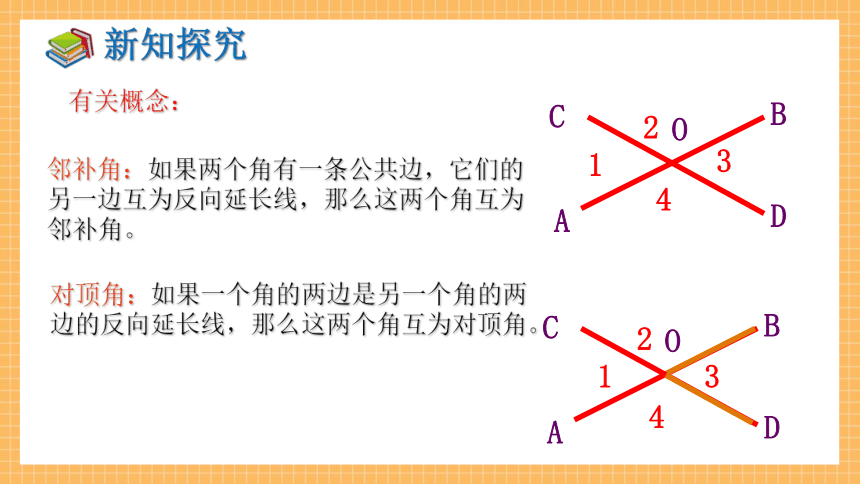
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
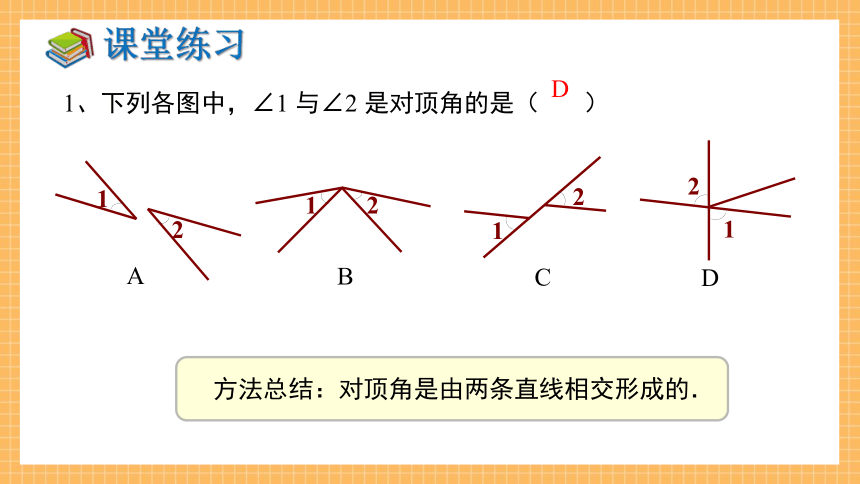
1、下列各图中,∠1 与∠2 是对顶角的是( )
D
1
2
A
1
2
B
方法总结:对顶角是由两条直线相交形成的.
1
2
D
1
2
C
∠1和∠3、∠2和∠4有什么关系?量一量或用其它的方法比较它们的大小. 完成下面的问题.
因为∠1+∠2=_______,
∠2+∠3=______(邻补角定义).
所以∠1=180°-______,
∠3=180°-_______(等式性质),
所以∠1=∠3(等量代换);
或者因为∠1与∠2互补,∠3与∠2互补(邻补角定义),
所以∠1=∠3(同角的补角相等).
180°
180°
∠2
∠2
对顶角相等
对顶角有如下性质:
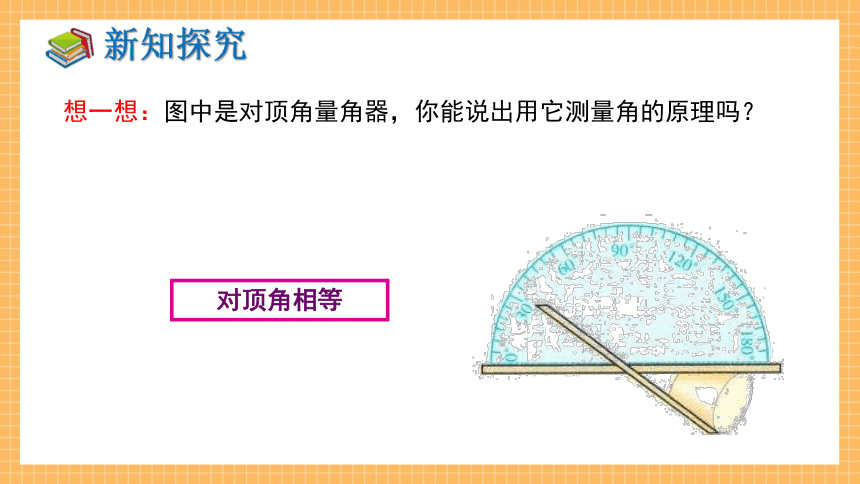
想一想:图中是对顶角量角器,你能说出用它测量角的原理吗?
对顶角相等
∠2 = 180°-∠1 = 140°.
a
b
)
(
1
3
4
2
)
(
2、如图,直线 a,b 相交,∠1 = 40°,求∠2,∠3,∠4 的度数.
∵ 直线 a 与 b 相交于一点,
∠1 = 40°,
∴∠3 =∠1 = 40°,
解:
∴∠4 =∠2 = 140°.
掌握对顶角的性质是解题的关键!
方法
课本P76“观察”:设直线AB,CD都与第三条直线MN相交(有时也说直线AB和CD被第三条直线MN所截),可以构成8个角,如图所示:(俗称“三线八角”)
N
3
4
A
B
C
D
M
1
2
5
6
7
8
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
1.图中的∠1 和∠5 的位置有什么关系?
我们把具有∠1 和∠5 这种位置关系的一对角叫做同位角.
3、下列图形中,∠1和∠2 是同位角的有( )
A
A. (1),(2) B. (3),(4)
C. (1),(2),(3) D. (2),(3),(4)
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
图中的 ∠1 与∠2 都是同位角.
1
2
1
2
1
2
1
2
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
2. ∠3与∠5,∠3与∠6的位置有什么关系呢?
我们把具有∠3和∠5这种位置关系的一对角叫做内错角.
4、如图,与∠1 是内错角关系的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
图中的 ∠1 与∠2 都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
2. ∠3与∠5,∠3与∠6的位置有什么关系呢?
我们把具有∠3和∠6这种位置关系的一对角叫做同旁内角.
5、下列图形中,∠1 和∠2 是同旁内角的是( )
1
1
A
B
C
D
1
2
2
2
1
2
A
图中的 ∠1 与∠2 都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
6、设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
你还能从图中找出其他的同位角、内错角和同旁内角吗?
同位角:∠2和∠6、∠3和∠7、∠4和∠8
内错角:∠4和∠6
同旁内角:∠4和∠5
角的名称 角的特征 基本 图形 形象记法 相同点 共同特征
同位角
同旁内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
①必有三条直线;
②这三类角都没有公共顶点;
③都表示角之间的位置关系
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
【例1】如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4,
∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,
∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
7、如图,直线 DE 截 AB ,AC,构成 8 个角,指出所有的同位角,内错角,同旁内角.
解:两条直线 AB,AC 被直线 DE 所截,所以 8 个角中,同位角有:∠1 与∠8,∠2 与∠5,∠3 与∠6,∠4 与∠7;内错角有:∠1 与∠6,∠4 与∠5;同旁内角有:∠1 与∠5,∠4 与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
8、识别哪些角是同位角、内错角、同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
【例2】如图,直线AB,CD被直线MN所截,同位角∠1与∠2相等,那么内错角∠2与∠3相等吗?
解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3(等量代换).
由上可知:两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
9、∠A 与∠8 是哪两条直线被哪条直线所截得的角 它们是什么关系的角 ∠A 与∠5 呢 ∠A 与∠4 呢
解:∠A 与∠8 是直线 AB,DE 被直线 AC 所截形成的内错角.
∠A 与∠5 是直线 AB,DE 被直线 AC 所截形成的同旁内角.
∠A 与∠4 是直线 AC,DE 被直线AB 所截形成的同位角.
E
D
C
B
A
8
7
6
5
4
3
2
1
3. 若 1: 2 = 2:7,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.
2. 若∠2 是 ∠1 的 3 倍,则∠1,∠2,∠3,∠4 各个角的度数分别为_____________________.
1. 若 ∠1 +∠3 = 60°,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.
30°,150°,30°,150°
45°,135°,45°,135°
40°,140°,40°,140°
4. 如图,∠DAB 和∠ABC 的位置关系是( )
A. 同位角 B. 同旁内角
C. 内错角 D. 以上结论都不对
5. 如图,∠1 和 ∠2 不能构成同位角的图形是( )
C
D
A
D
B
C
E
6、如图,直线 AB、CD,EF 相交于点 O,∠1=40°,∠BOC=110°,求∠2 的度数.
解:因为∠1=40°,
∠BOC=110° (已知),
所以∠BOF=∠BOC -∠1
=110°-40°=70°.
因为∠BOF=∠2 (对顶角相等),
所以∠2=70° (等量代换).
注意:隐含条件“对顶角相等”.
解:(1)∠AOC 的补角是∠AOD 和∠COB;
∠BOE 的补角是∠EOA 和∠BOF.
7. 如图,直线 AB,CD,EF 相交于点 O.
(1) 写出∠AOC,∠BOE 的补角;
(2) 写出∠DOA,∠EOC 的对顶角;
(3) 如果∠AOC = 50°,求∠BOD,∠COB 的度数.
A
E
D
B
F
C
O
(2)∠DOA 的对顶角是∠COB;
∠EOC 的对顶角是∠DOF.
(3)∠BOD =∠AOC = 50°,
∠COB = 180° -∠AOC = 130°.
8. 根据地图显示填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
9. 如图,直线 AB、CD、EF 相交,若∠1 +∠5 = 180°,
找出图中与∠1 相等的角.
解:∠1 =∠3 (对顶角相等).
D
B
E
A
C
F
1
2
3
4
5
6
8
7
因为∠5 +∠8 = 180°,且∠1 +∠5 = 180°,
所以∠8 =∠1.
因为∠8 =∠6 (对顶角相等),
所以∠6 =∠1.
综上可知,与∠1 相等的角有∠3,∠8,∠6.
10. 如图,直线 AB,CD 相交于点 O,∠EOC = 70°, OA 平分∠EOC ,求∠BOD 的度数.
A
B
C
D
E
O
解:因为 OA 平分∠EOC,
所以∠AOC = ∠EOC = 35°.
所以∠BOD =∠AOC = 35°.
对顶角
同位角
内错角
同旁内角
对顶角相等
两条直线被第三条直线所截,
如果有一对同位角相等,
则内错角相等.
1. 习题4.1中第4、5、6、10题.
2.完成同步练习册中本课时的练习.
4.1 平面上两条直线的位置关系
4.1.2 相交直线所成的角
1.理解对顶角、同位角、内错角、同旁内角的概念.
2.结合图形识别同位角、内错角、同旁内角.
3.经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理的表达能力.
4.培养学生的空间想象能力和数学思维能力.
【教学重点】同位角、内错角、同旁内角的识别.
【教学难点】分析图形.
1.在同一平面内的两条直线有几种位置关系?
2.经过直线外一点怎样画出这条直线的平行线?
3.如果两条直线都与第三条直线平行,那么这两条直线互相平行,
即如果 a∥b,b∥c,那么 a∥c.
阅读课本P75:如图4-7,剪刀的两个交叉腿构成四个角,将其简单地表示为图4-8.
图4-7
图4-8
1
2
3
4
A
B
C
D
1
2
3
4
A
B
C
D
∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
发现
图中还有哪些角也是邻补角呢?
1
2
3
4
A
B
C
D
O
发现
图中还有哪些角也是对顶角呢?
∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
O
A
B
C
D
1
3
4
2
O
A
B
C
D
1
3
4
2
有关概念:
邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。
对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
1、下列各图中,∠1 与∠2 是对顶角的是( )
D
1
2
A
1
2
B
方法总结:对顶角是由两条直线相交形成的.
1
2
D
1
2
C
∠1和∠3、∠2和∠4有什么关系?量一量或用其它的方法比较它们的大小. 完成下面的问题.
因为∠1+∠2=_______,
∠2+∠3=______(邻补角定义).
所以∠1=180°-______,
∠3=180°-_______(等式性质),
所以∠1=∠3(等量代换);
或者因为∠1与∠2互补,∠3与∠2互补(邻补角定义),
所以∠1=∠3(同角的补角相等).
180°
180°
∠2
∠2
对顶角相等
对顶角有如下性质:
想一想:图中是对顶角量角器,你能说出用它测量角的原理吗?
对顶角相等
∠2 = 180°-∠1 = 140°.
a
b
)
(
1
3
4
2
)
(
2、如图,直线 a,b 相交,∠1 = 40°,求∠2,∠3,∠4 的度数.
∵ 直线 a 与 b 相交于一点,
∠1 = 40°,
∴∠3 =∠1 = 40°,
解:
∴∠4 =∠2 = 140°.
掌握对顶角的性质是解题的关键!
方法
课本P76“观察”:设直线AB,CD都与第三条直线MN相交(有时也说直线AB和CD被第三条直线MN所截),可以构成8个角,如图所示:(俗称“三线八角”)
N
3
4
A
B
C
D
M
1
2
5
6
7
8
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
1.图中的∠1 和∠5 的位置有什么关系?
我们把具有∠1 和∠5 这种位置关系的一对角叫做同位角.
3、下列图形中,∠1和∠2 是同位角的有( )
A
A. (1),(2) B. (3),(4)
C. (1),(2),(3) D. (2),(3),(4)
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
图中的 ∠1 与∠2 都是同位角.
1
2
1
2
1
2
1
2
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
2. ∠3与∠5,∠3与∠6的位置有什么关系呢?
我们把具有∠3和∠5这种位置关系的一对角叫做内错角.
4、如图,与∠1 是内错角关系的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
图中的 ∠1 与∠2 都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
2. ∠3与∠5,∠3与∠6的位置有什么关系呢?
我们把具有∠3和∠6这种位置关系的一对角叫做同旁内角.
5、下列图形中,∠1 和∠2 是同旁内角的是( )
1
1
A
B
C
D
1
2
2
2
1
2
A
图中的 ∠1 与∠2 都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
6、设直线 AB, CD 都与第三条直线 MN 相交(有时也说直线 AB 和 CD 被第三条直线 MN 所截),可以构成 8 个角,如图所示.
你还能从图中找出其他的同位角、内错角和同旁内角吗?
同位角:∠2和∠6、∠3和∠7、∠4和∠8
内错角:∠4和∠6
同旁内角:∠4和∠5
角的名称 角的特征 基本 图形 形象记法 相同点 共同特征
同位角
同旁内角 内错角 F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
①必有三条直线;
②这三类角都没有公共顶点;
③都表示角之间的位置关系
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
【例1】如图,直线EF与AB,CD相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角有∠1和∠3,∠2和∠4,
∠5和∠7,∠6和∠8;
同位角有∠2和∠5,∠1和∠8,
∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
7、如图,直线 DE 截 AB ,AC,构成 8 个角,指出所有的同位角,内错角,同旁内角.
解:两条直线 AB,AC 被直线 DE 所截,所以 8 个角中,同位角有:∠1 与∠8,∠2 与∠5,∠3 与∠6,∠4 与∠7;内错角有:∠1 与∠6,∠4 与∠5;同旁内角有:∠1 与∠5,∠4 与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
8、识别哪些角是同位角、内错角、同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
【例2】如图,直线AB,CD被直线MN所截,同位角∠1与∠2相等,那么内错角∠2与∠3相等吗?
解:因为∠1=∠3(对顶角相等),
∠1=∠2(已知),
所以∠2=∠3(等量代换).
由上可知:两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
9、∠A 与∠8 是哪两条直线被哪条直线所截得的角 它们是什么关系的角 ∠A 与∠5 呢 ∠A 与∠4 呢
解:∠A 与∠8 是直线 AB,DE 被直线 AC 所截形成的内错角.
∠A 与∠5 是直线 AB,DE 被直线 AC 所截形成的同旁内角.
∠A 与∠4 是直线 AC,DE 被直线AB 所截形成的同位角.
E
D
C
B
A
8
7
6
5
4
3
2
1
3. 若 1: 2 = 2:7,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.
2. 若∠2 是 ∠1 的 3 倍,则∠1,∠2,∠3,∠4 各个角的度数分别为_____________________.
1. 若 ∠1 +∠3 = 60°,则∠1,∠2,∠3,∠4 各角的度数分别为_____________________.
30°,150°,30°,150°
45°,135°,45°,135°
40°,140°,40°,140°
4. 如图,∠DAB 和∠ABC 的位置关系是( )
A. 同位角 B. 同旁内角
C. 内错角 D. 以上结论都不对
5. 如图,∠1 和 ∠2 不能构成同位角的图形是( )
C
D
A
D
B
C
E
6、如图,直线 AB、CD,EF 相交于点 O,∠1=40°,∠BOC=110°,求∠2 的度数.
解:因为∠1=40°,
∠BOC=110° (已知),
所以∠BOF=∠BOC -∠1
=110°-40°=70°.
因为∠BOF=∠2 (对顶角相等),
所以∠2=70° (等量代换).
注意:隐含条件“对顶角相等”.
解:(1)∠AOC 的补角是∠AOD 和∠COB;
∠BOE 的补角是∠EOA 和∠BOF.
7. 如图,直线 AB,CD,EF 相交于点 O.
(1) 写出∠AOC,∠BOE 的补角;
(2) 写出∠DOA,∠EOC 的对顶角;
(3) 如果∠AOC = 50°,求∠BOD,∠COB 的度数.
A
E
D
B
F
C
O
(2)∠DOA 的对顶角是∠COB;
∠EOC 的对顶角是∠DOF.
(3)∠BOD =∠AOC = 50°,
∠COB = 180° -∠AOC = 130°.
8. 根据地图显示填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
9. 如图,直线 AB、CD、EF 相交,若∠1 +∠5 = 180°,
找出图中与∠1 相等的角.
解:∠1 =∠3 (对顶角相等).
D
B
E
A
C
F
1
2
3
4
5
6
8
7
因为∠5 +∠8 = 180°,且∠1 +∠5 = 180°,
所以∠8 =∠1.
因为∠8 =∠6 (对顶角相等),
所以∠6 =∠1.
综上可知,与∠1 相等的角有∠3,∠8,∠6.
10. 如图,直线 AB,CD 相交于点 O,∠EOC = 70°, OA 平分∠EOC ,求∠BOD 的度数.
A
B
C
D
E
O
解:因为 OA 平分∠EOC,
所以∠AOC = ∠EOC = 35°.
所以∠BOD =∠AOC = 35°.
对顶角
同位角
内错角
同旁内角
对顶角相等
两条直线被第三条直线所截,
如果有一对同位角相等,
则内错角相等.
1. 习题4.1中第4、5、6、10题.
2.完成同步练习册中本课时的练习.
