安徽省合肥市重点学校2023-2024学年九年级上学期期末数学试题(无答案)
文档属性
| 名称 | 安徽省合肥市重点学校2023-2024学年九年级上学期期末数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 10:13:25 | ||
图片预览

文档简介
2023-2024学年第一学期九年级期末学业质量检测
数学试题
注意事项:1.你拿到的试卷满分为150分,考试时间为120分钟.
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共4页.
3.请务必在“答题卷”上答题,在“试题卷”上答题无效.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(每小题4分,共40分)
1.逢年过节抑或新婚喜庆,人们把美丽鲜艳的剪纸贴在雪白的窗纸或明亮的玻璃窗上、墙上、门上、灯笼上,节日的气氛便被渲染得非常浓郁喜庆。在下列四幅剪纸中,为中心对称图形的是( )
A. B. C. D.
2.下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
3.在中中,,,,那么的值是( )
A. B. C. D.
4.若在反比例函数图象的任一支上,y都随x的增大而增大,则下列点可能在这个函数图象上的为( )
A. B. C. D.
5.如图所示,A、B、C、D是一个外角为40°的正多边形的顶点.若O为正多边形的中心,则的度数为( )
A.15° B.20° C.30° D.40°
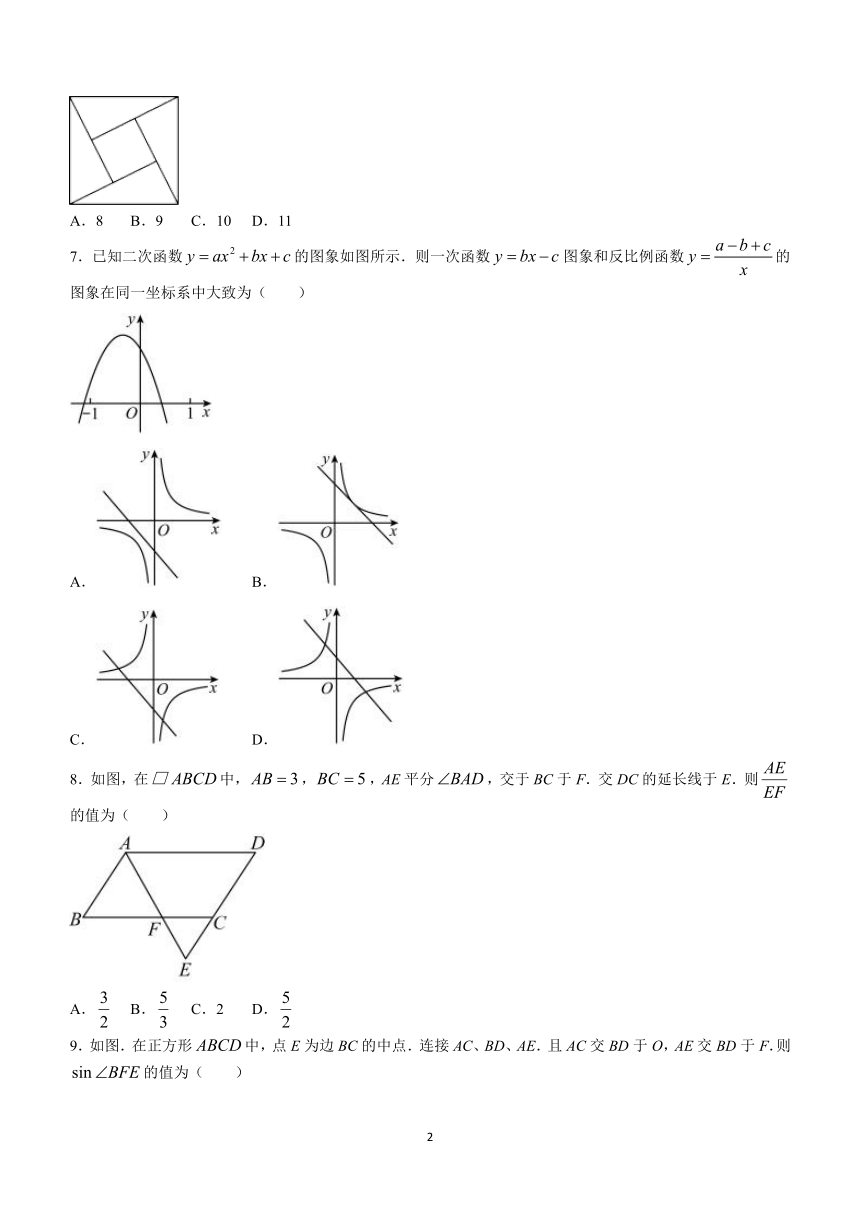
6.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为a.较短直角边长为b,若,大正方形的面积为129.则小正方形的边长为( )
A.8 B.9 C.10 D.11
7.已知二次函数的图象如图所示.则一次函数图象和反比例函数的图象在同一坐标系中大致为( )
A. B.
C. D.
8.如图,在中,,,AE平分,交于BC于F.交DC的延长线于E.则的值为( )
A. B. C.2 D.
9.如图.在正方形中,点E为边BC的中点.连接AC、BD、AE.且AC交BD于O,AE交BD于F.则的值为( )
A. B. C. D.
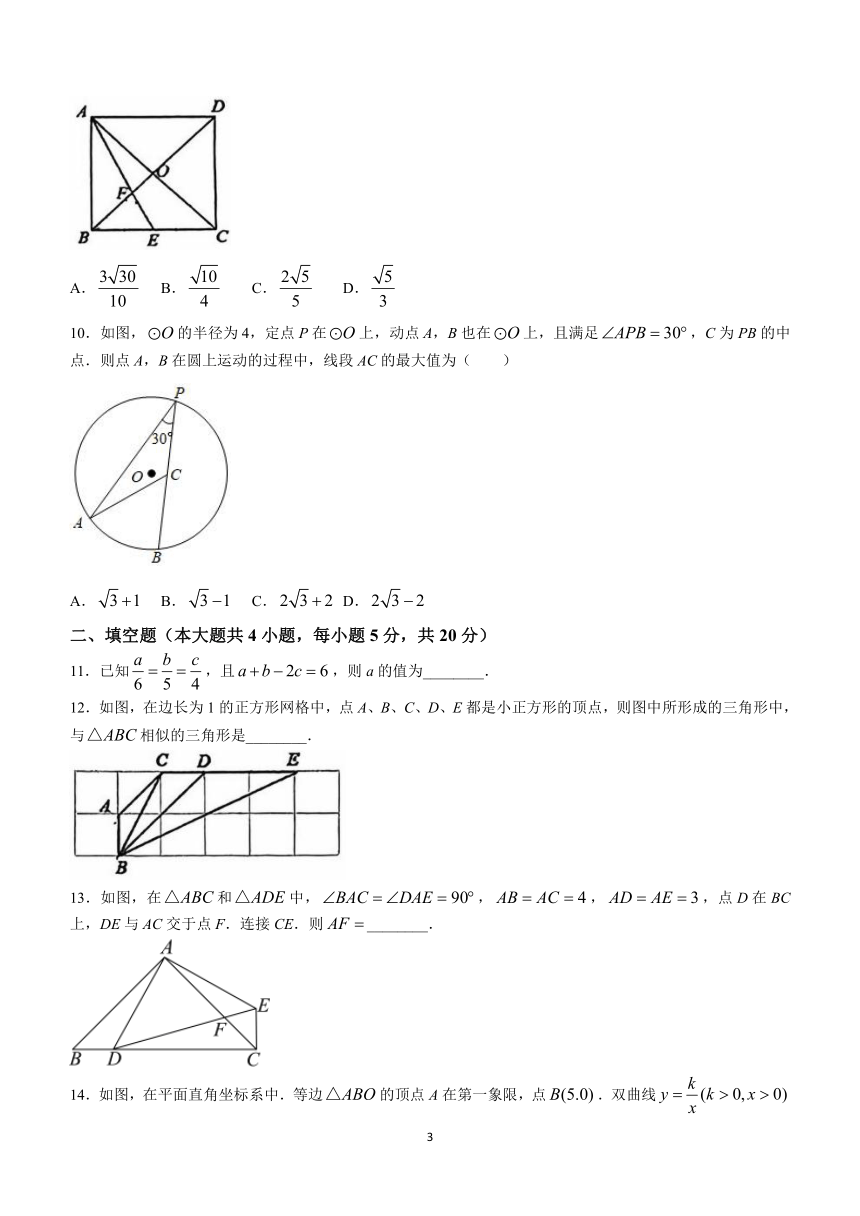
10.如图,的半径为4,定点P在上,动点A,B也在上,且满足,C为PB的中点.则点A,B在圆上运动的过程中,线段AC的最大值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知,且,则a的值为________.
12.如图,在边长为1的正方形网格中,点A、B、C、D、E都是小正方形的顶点,则图中所形成的三角形中,与相似的三角形是________.
13.如图,在和中,,,,点D在BC上,DE与AC交于点F.连接CE.则________.
14.如图,在平面直角坐标系中.等边的顶点A在第一象限,点.双曲线把分成两部分,若.
(1)双曲线与边OA,AB分别交于C.D两点,k的值为________.
(2)连接CD,则的面积为________.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:
16.羽毛球运动是一项很好的健身项目,羽毛球发球时,羽毛球飞行路线为抛物线的一部分,如图,一运动员站在O点发球.且羽毛球飞行高度y(m)与水平距离x(m)之间满足函数关系式.
(1)求羽毛球飞行路线中离地最大高度.
(2)已知羽毛球球网高度为1.55m.发球点A与球网的水平距离为3m,通过计算说明这次发球是否能过网?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的;
(2)画出绕O点顺时针旋转90°后得到的.
18.如图.为测量学校旗杆AB的高度.小明从旗杆正前方8米处的点C出发,沿坡度为的斜坡CD前进8米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与水平地面BC垂直.
(1)求点D的铅垂高度;
(2)求旗杆AB的高度.(结果精确到0.1米.参考数据:,,,,.)
五、(本大题共2小题,每小题10分,满分20分)
19.如图在中,D为BC上一点,AD平分,.
(1)求证:;
(2)若,.求的长.
20.如图,内接于.AB为直径,过O作,交BC的延长线于点D.过C作的切线交OD于点E.
(1)求证:;
(2)若的半径为8.,求AC的长.
六、(本题满分12分)
21.一次函数的图象与反比例函数的图象交于,.与x轴交于C.
(1)求a,b,k的值;
(2)观察图象,直接写出不等式的解集;
(3)延长BO交反比例函数图象于点P.求的面积.
七、(本题满分12分)
22.在矩形的CD边上取一点E,将沿BE翻折,使C点恰好落在AD边上点F处,且。
图1 图2 图3
(1)如图1,若,求的度数;
(2)如图2.当,且时.求BC的长;
(3)如图3,作的角平分线交AD于点N,若,.求AB的值.
八、(本题满分14分)
23.平面直角坐标系中,点O是坐标原点,抛物线与y轴交于,与x轴交于B、C两点(C在B的右侧),顶点坐标为。
(1)求抛物线解析式;
(2)点E是抛物线上一动点,且位于直线AC的上方,过点E作AC的垂线交AC于点F,求EF长度的最大值;
(3)在直线AC上是否存在点G,使得?若存在,请求出点G的坐标;若不存在,请说明理由.
数学试题
注意事项:1.你拿到的试卷满分为150分,考试时间为120分钟.
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共4页.
3.请务必在“答题卷”上答题,在“试题卷”上答题无效.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(每小题4分,共40分)
1.逢年过节抑或新婚喜庆,人们把美丽鲜艳的剪纸贴在雪白的窗纸或明亮的玻璃窗上、墙上、门上、灯笼上,节日的气氛便被渲染得非常浓郁喜庆。在下列四幅剪纸中,为中心对称图形的是( )
A. B. C. D.
2.下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
3.在中中,,,,那么的值是( )
A. B. C. D.
4.若在反比例函数图象的任一支上,y都随x的增大而增大,则下列点可能在这个函数图象上的为( )
A. B. C. D.
5.如图所示,A、B、C、D是一个外角为40°的正多边形的顶点.若O为正多边形的中心,则的度数为( )
A.15° B.20° C.30° D.40°
6.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形,设直角三角形较长直角边长为a.较短直角边长为b,若,大正方形的面积为129.则小正方形的边长为( )
A.8 B.9 C.10 D.11
7.已知二次函数的图象如图所示.则一次函数图象和反比例函数的图象在同一坐标系中大致为( )
A. B.
C. D.
8.如图,在中,,,AE平分,交于BC于F.交DC的延长线于E.则的值为( )
A. B. C.2 D.
9.如图.在正方形中,点E为边BC的中点.连接AC、BD、AE.且AC交BD于O,AE交BD于F.则的值为( )
A. B. C. D.
10.如图,的半径为4,定点P在上,动点A,B也在上,且满足,C为PB的中点.则点A,B在圆上运动的过程中,线段AC的最大值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11.已知,且,则a的值为________.
12.如图,在边长为1的正方形网格中,点A、B、C、D、E都是小正方形的顶点,则图中所形成的三角形中,与相似的三角形是________.
13.如图,在和中,,,,点D在BC上,DE与AC交于点F.连接CE.则________.
14.如图,在平面直角坐标系中.等边的顶点A在第一象限,点.双曲线把分成两部分,若.
(1)双曲线与边OA,AB分别交于C.D两点,k的值为________.
(2)连接CD,则的面积为________.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:
16.羽毛球运动是一项很好的健身项目,羽毛球发球时,羽毛球飞行路线为抛物线的一部分,如图,一运动员站在O点发球.且羽毛球飞行高度y(m)与水平距离x(m)之间满足函数关系式.
(1)求羽毛球飞行路线中离地最大高度.
(2)已知羽毛球球网高度为1.55m.发球点A与球网的水平距离为3m,通过计算说明这次发球是否能过网?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的;
(2)画出绕O点顺时针旋转90°后得到的.
18.如图.为测量学校旗杆AB的高度.小明从旗杆正前方8米处的点C出发,沿坡度为的斜坡CD前进8米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与水平地面BC垂直.
(1)求点D的铅垂高度;
(2)求旗杆AB的高度.(结果精确到0.1米.参考数据:,,,,.)
五、(本大题共2小题,每小题10分,满分20分)
19.如图在中,D为BC上一点,AD平分,.
(1)求证:;
(2)若,.求的长.
20.如图,内接于.AB为直径,过O作,交BC的延长线于点D.过C作的切线交OD于点E.
(1)求证:;
(2)若的半径为8.,求AC的长.
六、(本题满分12分)
21.一次函数的图象与反比例函数的图象交于,.与x轴交于C.
(1)求a,b,k的值;
(2)观察图象,直接写出不等式的解集;
(3)延长BO交反比例函数图象于点P.求的面积.
七、(本题满分12分)
22.在矩形的CD边上取一点E,将沿BE翻折,使C点恰好落在AD边上点F处,且。
图1 图2 图3
(1)如图1,若,求的度数;
(2)如图2.当,且时.求BC的长;
(3)如图3,作的角平分线交AD于点N,若,.求AB的值.
八、(本题满分14分)
23.平面直角坐标系中,点O是坐标原点,抛物线与y轴交于,与x轴交于B、C两点(C在B的右侧),顶点坐标为。
(1)求抛物线解析式;
(2)点E是抛物线上一动点,且位于直线AC的上方,过点E作AC的垂线交AC于点F,求EF长度的最大值;
(3)在直线AC上是否存在点G,使得?若存在,请求出点G的坐标;若不存在,请说明理由.
同课章节目录
