《圆柱》常考题型(同步练习) 六年级下册数学人教版(无答案)
文档属性
| 名称 | 《圆柱》常考题型(同步练习) 六年级下册数学人教版(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 06:58:40 | ||
图片预览




文档简介
六下第三单元《圆柱》常考题型
【题型一:圆柱的认识】
圆柱有三个部分组成,即底面、侧面、高:
1、圆柱是由( )个面围成的。圆柱的上、下两个面叫做( )。圆柱周围的面(上、下底面除外)叫做( )。圆柱的两个底面之间的距离叫做( ),圆柱有( )条高。
【题型二:圆柱的侧面展开图】
圆柱的侧面展开图:
①当沿高展开时,展开图是长方形;
②当底面周长和高相等时,沿高展开图是正方形;
③当不沿高展开时(斜向切开),展开图是平行四边形。
圆柱的底面半径是,高是,它的侧面展开图是一个长方形。这个长方形的长是( ),宽是( )。
把一个圆柱的侧面展开后是一个边长为62.8厘米的正方形,这个圆柱的底面半径是( )厘米。
【题型二:圆柱的侧面积】
当圆柱沿高展开时,展开图是一个长方形,其中长方形的长等于圆柱的底面周长,宽等于圆柱的高,因此:
圆柱的侧面积=长方形的面积=长×宽=圆柱底面的周长×高
S侧=Ch=2πrh。
1、一个圆柱的底面半径是4分米,高是6分米,这个圆柱的侧面积是( )平方分米。
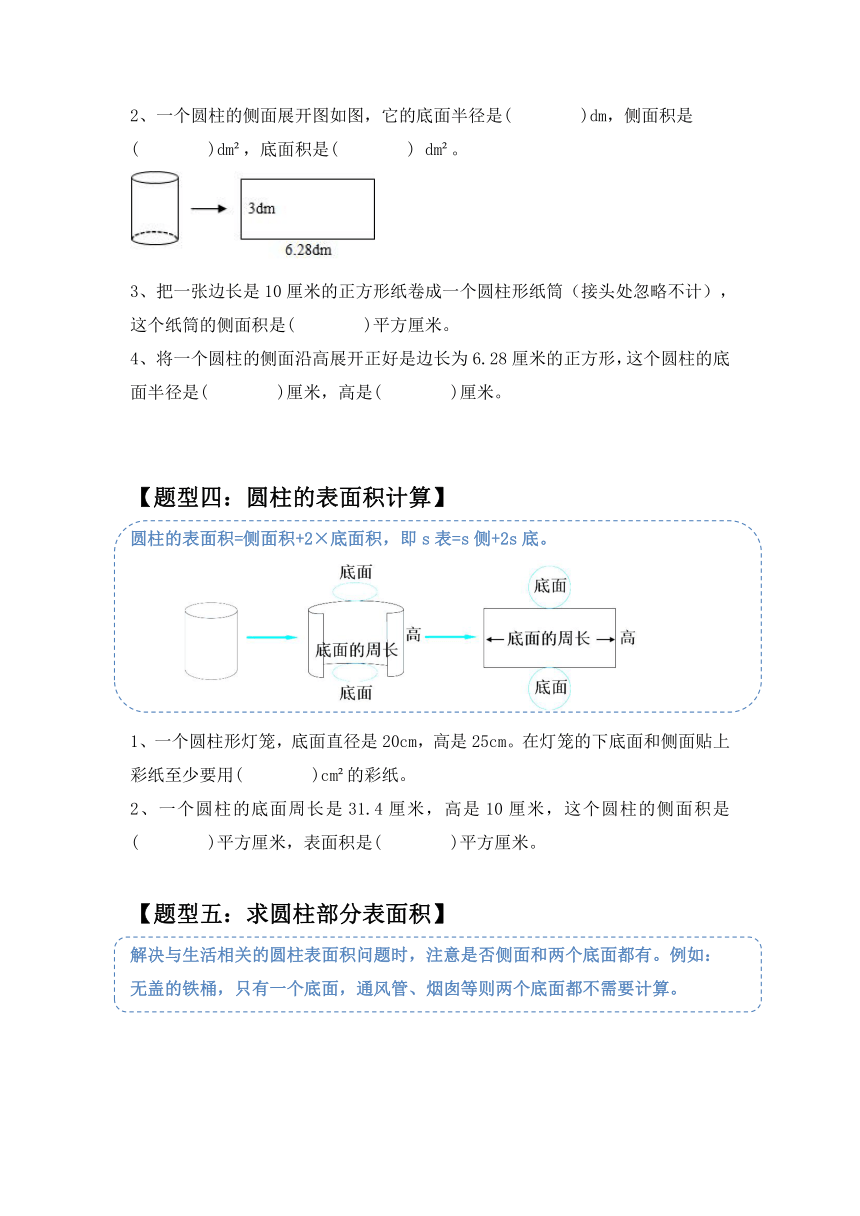
2、一个圆柱的侧面展开图如图,它的底面半径是( )dm,侧面积是( )dm ,底面积是( ) dm 。
把一张边长是10厘米的正方形纸卷成一个圆柱形纸筒(接头处忽略不计),这个纸筒的侧面积是( )平方厘米。
将一个圆柱的侧面沿高展开正好是边长为6.28厘米的正方形,这个圆柱的底面半径是( )厘米,高是( )厘米。
【题型四:圆柱的表面积计算】
圆柱的表面积=侧面积+2×底面积,即s表=s侧+2s底。
1、一个圆柱形灯笼,底面直径是20cm,高是25cm。在灯笼的下底面和侧面贴上彩纸至少要用( )cm 的彩纸。
2、一个圆柱的底面周长是31.4厘米,高是10厘米,这个圆柱的侧面积是( )平方厘米,表面积是( )平方厘米。
【题型五:求圆柱部分表面积】
解决与生活相关的圆柱表面积问题时,注意是否侧面和两个底面都有。例如:无盖的铁桶,只有一个底面,通风管、烟囱等则两个底面都不需要计算。
1、一个圆柱形的玻璃鱼缸(无盖),底面半径2分米,高3分米。做这样一个鱼缸至少需要多少平方分米玻璃?
2、修建一个圆柱形的蓄水池,底面直径是4米,深5米。在蓄水池的四周与下底面抹上水泥,抹水泥部分的面积是多少平方米?如果每平方米用水泥0.75千克,一共需要多少千克水泥?
3、用铁皮制作圆柱形通风管,底面半径4分米,每节长50分米,制作10节这样的通风管,至少需要多少平方米的铁皮?
4、一台压路机,前轮直径2米,轮宽1.2米,工作时每分钟滚动18周。这台压路机工作1分钟前进多少米?工作1分钟前轮压过的路面是多少平方米?
5、用彩带捆扎一个圆柱形的礼品盒(如图)。打结处正好是底面圆心,打结用去彩带25厘米。
捆扎这个礼品盒至少用去彩带多少厘米?
(2)在蛋糕盒的整个侧面贴上商标纸(结头处重合2厘米),商标纸的面积是多少平方厘米?
【题型六:圆柱的体积】
圆柱体积的意义和计算公式
(1)意义∶一个圆柱所占空间的大小,叫做这个圆柱的体积。
(2)计算公式的字母表达式∶如果用V表示圆柱的体积,用S表示圆柱的底面积,用h表示圆柱的高,则圆柱的体积=底面积×高,字母表示为V=Sh=πr h。
1、一个圆柱的底面半径是5厘米,高是10厘米,它的底面积是( )平方厘米,侧面积是( )平方厘米,体积是( )立方厘米。
2、一个圆柱的底面周长是18.84厘米,高是8厘米,则它的表面积是( )平方厘米,体积是( )立方厘米。
3、一个圆柱体,侧面积是37.68cm2,高是6cm,底面周长是( )cm,体积是( )cm3。
【题型七:已知体积,求高或底面积】
根据圆柱的体积公式=底面积×高,用字母表示为V=Sh,可将体积公式变形反求底面积或高,即:
①S底=V柱÷h
②h=V柱÷S底。
1、一块铁块的体积是108dm3,把这块铁块制成一个底面积是72dm2的圆柱形零件,这个零件高多少厘米?
2、一个圆柱形铁罐的容积是1升,高是12厘米.铁罐的底面积大约是多少平方厘米?
3、一个装满汽油的圆柱形油桶,从里面量,底面半径为10分米,如果用去这桶油的后,还剩628升,这个油桶的高是多少?
【题型七:组合立体图形表面积、体积】
1、求下面图形的表面积和体积。
2、计算下面钢管所用钢材的体积。(单位:cm)
3、有一个工具箱下半部分为正方体,上半部分为圆柱体一半(下图),如果把工具箱的表面涂上油漆(包括底面),求涂油漆部分的面积。
4、下面是一个零件的示意图(单位:厘米),是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的表面积和体积。(π取3.14)
【题型八:圆柱展开图求体积】
在有展开图时,关键在于找出圆柱底面圆的半径和高,再根据圆柱的体积公式进行计算。
1、乐乐用一张长方形硬纸板按下图的方法剪下来正好做成了一个圆柱,这个圆柱的侧面积是多少平方厘米?体积是多少立方厘米?
2、如下图,是一个圆柱展开图(单位:cm),求圆柱的体积。
3、如下图,一块长方形的铁皮,利用图中的涂色部分刚好能做一个无盖的圆柱形水桶。这个水桶的容积是多少升?(接头处忽略不计)
【题型九:圆柱的表面积增减变化(切、拼)】
1.圆柱高的变化引起表面积的变化:
由于底面积没有变,所以实际上发生变化的是侧面积,由此可以求出底面周长,进而求出表面积,即底面周长C=变化的表面积÷变化的高度。
2.横切引起的表面积变化。
平行于底面切(横切)一刀,多出的两个面是底面,即两个圆。
3.竖切引起的表面积变化。
垂直于底面切(竖切),多出的两个面是长方形,即以底面圆的直径为长,以圆柱的高为宽的长方形。
康康把一块橡皮泥揉成圆柱形,切成三块(如图1),表面积增加了50.24平方厘米;切成四块(如图2),表面积增加了48平方厘米。圆柱形橡皮泥的体积是多少立方厘米?
如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
【题型十:圆柱与长方体的拼切转化问题】
将一个底面半径为r,高为h的圆柱沿着高切成若干等份,并将其拼成一个近似的长方体,此时这个圆柱和长方体的体积相等,拼成的长方体的表面积比圆柱多2个面积大小为hr的长方形。
1、将一个高是12厘米的圆柱体如图那样切拼,切拼后的立体图形的表面积比圆柱体大120平方厘米。求圆柱体的体积。(π取3.14)
【题型十一:排水法求不规则物体的体积】
形状不规则的物体可以用排水法求体积,排水法的公式:
①V物体=V现在-V原来
②V物体=S×(h现在- h原来)
③V物体=S×h升高
1、一个底面半径是20厘米、高是30厘米的圆柱形鱼缸里装有一些水,向鱼缸里放入一块鹅卵石(完全浸入水中),水面上升了1.5厘米。这块鹅卵石的体积是多少立方厘米?
2、有一只底面半径为3dm的圆柱形水桶,桶内盛满水,并浸有一块底面为正方形边长为2dm的长方体铁块(完全浸没水中)。当铁块从水中完全取出时,桶内的水面下降了5cm,求这块长方体铁块的高。(得数保留一位小数)
【题型十二:等积转化问题】
圆柱与长方体、正方体的等积转化问题,找到题目中的体积不变量,再根据体积不变解决问题。
1、把一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铅块和一个棱长是5厘米的正方体铅块,铸成一个圆柱。这个圆柱的底面直径是20厘米,高是多少厘米?
2、甲圆柱形瓶子中有2厘米深的水。将甲瓶中的水全部倒入甲瓶,这时乙瓶的水深多少厘米?(如图)
3、一个高30cm的酒瓶中盛有酒,如果把它倒置在桌面上(如图所示),求酒瓶的容积是多少?
【题型一:圆柱的认识】
圆柱有三个部分组成,即底面、侧面、高:
1、圆柱是由( )个面围成的。圆柱的上、下两个面叫做( )。圆柱周围的面(上、下底面除外)叫做( )。圆柱的两个底面之间的距离叫做( ),圆柱有( )条高。
【题型二:圆柱的侧面展开图】
圆柱的侧面展开图:
①当沿高展开时,展开图是长方形;
②当底面周长和高相等时,沿高展开图是正方形;
③当不沿高展开时(斜向切开),展开图是平行四边形。
圆柱的底面半径是,高是,它的侧面展开图是一个长方形。这个长方形的长是( ),宽是( )。
把一个圆柱的侧面展开后是一个边长为62.8厘米的正方形,这个圆柱的底面半径是( )厘米。
【题型二:圆柱的侧面积】
当圆柱沿高展开时,展开图是一个长方形,其中长方形的长等于圆柱的底面周长,宽等于圆柱的高,因此:
圆柱的侧面积=长方形的面积=长×宽=圆柱底面的周长×高
S侧=Ch=2πrh。
1、一个圆柱的底面半径是4分米,高是6分米,这个圆柱的侧面积是( )平方分米。
2、一个圆柱的侧面展开图如图,它的底面半径是( )dm,侧面积是( )dm ,底面积是( ) dm 。
把一张边长是10厘米的正方形纸卷成一个圆柱形纸筒(接头处忽略不计),这个纸筒的侧面积是( )平方厘米。
将一个圆柱的侧面沿高展开正好是边长为6.28厘米的正方形,这个圆柱的底面半径是( )厘米,高是( )厘米。
【题型四:圆柱的表面积计算】
圆柱的表面积=侧面积+2×底面积,即s表=s侧+2s底。
1、一个圆柱形灯笼,底面直径是20cm,高是25cm。在灯笼的下底面和侧面贴上彩纸至少要用( )cm 的彩纸。
2、一个圆柱的底面周长是31.4厘米,高是10厘米,这个圆柱的侧面积是( )平方厘米,表面积是( )平方厘米。
【题型五:求圆柱部分表面积】
解决与生活相关的圆柱表面积问题时,注意是否侧面和两个底面都有。例如:无盖的铁桶,只有一个底面,通风管、烟囱等则两个底面都不需要计算。
1、一个圆柱形的玻璃鱼缸(无盖),底面半径2分米,高3分米。做这样一个鱼缸至少需要多少平方分米玻璃?
2、修建一个圆柱形的蓄水池,底面直径是4米,深5米。在蓄水池的四周与下底面抹上水泥,抹水泥部分的面积是多少平方米?如果每平方米用水泥0.75千克,一共需要多少千克水泥?
3、用铁皮制作圆柱形通风管,底面半径4分米,每节长50分米,制作10节这样的通风管,至少需要多少平方米的铁皮?
4、一台压路机,前轮直径2米,轮宽1.2米,工作时每分钟滚动18周。这台压路机工作1分钟前进多少米?工作1分钟前轮压过的路面是多少平方米?
5、用彩带捆扎一个圆柱形的礼品盒(如图)。打结处正好是底面圆心,打结用去彩带25厘米。
捆扎这个礼品盒至少用去彩带多少厘米?
(2)在蛋糕盒的整个侧面贴上商标纸(结头处重合2厘米),商标纸的面积是多少平方厘米?
【题型六:圆柱的体积】
圆柱体积的意义和计算公式
(1)意义∶一个圆柱所占空间的大小,叫做这个圆柱的体积。
(2)计算公式的字母表达式∶如果用V表示圆柱的体积,用S表示圆柱的底面积,用h表示圆柱的高,则圆柱的体积=底面积×高,字母表示为V=Sh=πr h。
1、一个圆柱的底面半径是5厘米,高是10厘米,它的底面积是( )平方厘米,侧面积是( )平方厘米,体积是( )立方厘米。
2、一个圆柱的底面周长是18.84厘米,高是8厘米,则它的表面积是( )平方厘米,体积是( )立方厘米。
3、一个圆柱体,侧面积是37.68cm2,高是6cm,底面周长是( )cm,体积是( )cm3。
【题型七:已知体积,求高或底面积】
根据圆柱的体积公式=底面积×高,用字母表示为V=Sh,可将体积公式变形反求底面积或高,即:
①S底=V柱÷h
②h=V柱÷S底。
1、一块铁块的体积是108dm3,把这块铁块制成一个底面积是72dm2的圆柱形零件,这个零件高多少厘米?
2、一个圆柱形铁罐的容积是1升,高是12厘米.铁罐的底面积大约是多少平方厘米?
3、一个装满汽油的圆柱形油桶,从里面量,底面半径为10分米,如果用去这桶油的后,还剩628升,这个油桶的高是多少?
【题型七:组合立体图形表面积、体积】
1、求下面图形的表面积和体积。
2、计算下面钢管所用钢材的体积。(单位:cm)
3、有一个工具箱下半部分为正方体,上半部分为圆柱体一半(下图),如果把工具箱的表面涂上油漆(包括底面),求涂油漆部分的面积。
4、下面是一个零件的示意图(单位:厘米),是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的表面积和体积。(π取3.14)
【题型八:圆柱展开图求体积】
在有展开图时,关键在于找出圆柱底面圆的半径和高,再根据圆柱的体积公式进行计算。
1、乐乐用一张长方形硬纸板按下图的方法剪下来正好做成了一个圆柱,这个圆柱的侧面积是多少平方厘米?体积是多少立方厘米?
2、如下图,是一个圆柱展开图(单位:cm),求圆柱的体积。
3、如下图,一块长方形的铁皮,利用图中的涂色部分刚好能做一个无盖的圆柱形水桶。这个水桶的容积是多少升?(接头处忽略不计)
【题型九:圆柱的表面积增减变化(切、拼)】
1.圆柱高的变化引起表面积的变化:
由于底面积没有变,所以实际上发生变化的是侧面积,由此可以求出底面周长,进而求出表面积,即底面周长C=变化的表面积÷变化的高度。
2.横切引起的表面积变化。
平行于底面切(横切)一刀,多出的两个面是底面,即两个圆。
3.竖切引起的表面积变化。
垂直于底面切(竖切),多出的两个面是长方形,即以底面圆的直径为长,以圆柱的高为宽的长方形。
康康把一块橡皮泥揉成圆柱形,切成三块(如图1),表面积增加了50.24平方厘米;切成四块(如图2),表面积增加了48平方厘米。圆柱形橡皮泥的体积是多少立方厘米?
如图,一个圆柱高10厘米,如果它的高增加4厘米,那么它的表面积将增加50.24平方厘米,求原来圆柱的体积是多少立方厘米?
【题型十:圆柱与长方体的拼切转化问题】
将一个底面半径为r,高为h的圆柱沿着高切成若干等份,并将其拼成一个近似的长方体,此时这个圆柱和长方体的体积相等,拼成的长方体的表面积比圆柱多2个面积大小为hr的长方形。
1、将一个高是12厘米的圆柱体如图那样切拼,切拼后的立体图形的表面积比圆柱体大120平方厘米。求圆柱体的体积。(π取3.14)
【题型十一:排水法求不规则物体的体积】
形状不规则的物体可以用排水法求体积,排水法的公式:
①V物体=V现在-V原来
②V物体=S×(h现在- h原来)
③V物体=S×h升高
1、一个底面半径是20厘米、高是30厘米的圆柱形鱼缸里装有一些水,向鱼缸里放入一块鹅卵石(完全浸入水中),水面上升了1.5厘米。这块鹅卵石的体积是多少立方厘米?
2、有一只底面半径为3dm的圆柱形水桶,桶内盛满水,并浸有一块底面为正方形边长为2dm的长方体铁块(完全浸没水中)。当铁块从水中完全取出时,桶内的水面下降了5cm,求这块长方体铁块的高。(得数保留一位小数)
【题型十二:等积转化问题】
圆柱与长方体、正方体的等积转化问题,找到题目中的体积不变量,再根据体积不变解决问题。
1、把一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铅块和一个棱长是5厘米的正方体铅块,铸成一个圆柱。这个圆柱的底面直径是20厘米,高是多少厘米?
2、甲圆柱形瓶子中有2厘米深的水。将甲瓶中的水全部倒入甲瓶,这时乙瓶的水深多少厘米?(如图)
3、一个高30cm的酒瓶中盛有酒,如果把它倒置在桌面上(如图所示),求酒瓶的容积是多少?
