20.3 体质健康测试中的数据分析同步练习(含解析)
文档属性
| 名称 | 20.3 体质健康测试中的数据分析同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
20.3 体质健康测试中的数据分析
一、单选题
1.关于数据3, , ,0,5的说法正确的是( )
A.平均数为 B.中位数为1
C.众数为5 D.方差为6.8
2.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在以下统计量中,该鞋厂最关注的是( )
A.平均数 B.中位数 C.众数 D.方差
3.学校组织才艺表演比赛,前5名获奖.有11位同学参加比赛且他们所得的分数互不相同.某同学知道自己的比赛分数后,要判断自己能否获奖,在这11名同学成绩的统计量中只需知道一个量,它是( )
A.众数 B.方差 C.中位数 D.平均数
4.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩是0.9环.方差分别0.56、0.78、0.42、0.63,这四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
5.如图是甲乙两位同学在参加体育中考前的次体能测试成绩折线统计图,由图可知, 的成绩更稳定.
6.某校射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛,在选拔赛中每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
甲 乙 丙 丁
平均数 8.2 8.0 8.2 8.0
方差 2.0 1.8 1.5 1.6
请你根据表中数据选择其中一人参加比赛,最合适的人选是 .
7.甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为 ,则这6次比赛成绩比较稳定的是 .(填“甲”或“乙”)
8.某跳远队甲、乙两名运动员最近 10 次跳远成绩的平均数均为 402 cm,若甲跳远成绩的方差为S甲2 =66.73,乙跳远成绩的方差为S乙2 =85.21,则成绩比较稳定的是 .(填“甲”或“乙”)
三、解答题
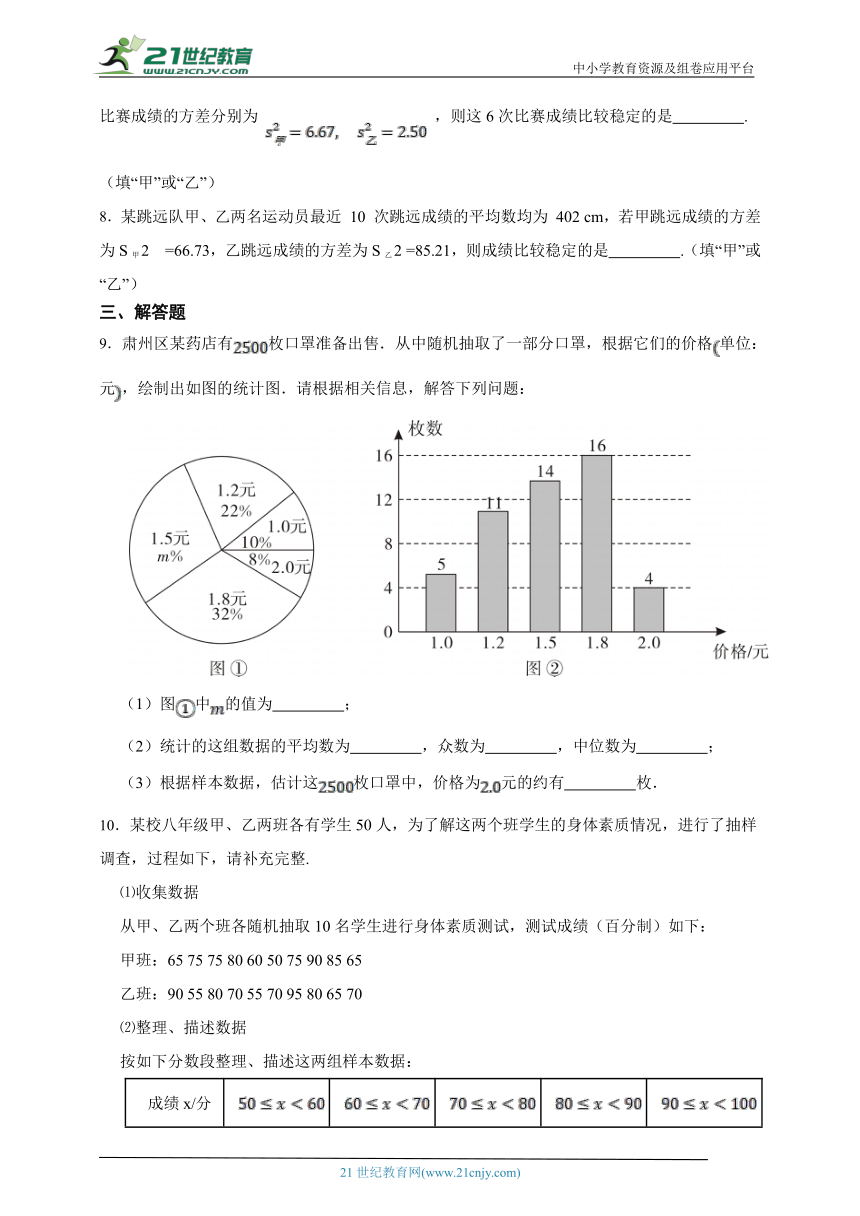
9.肃州区某药店有枚口罩准备出售.从中随机抽取了一部分口罩,根据它们的价格单位:元,绘制出如图的统计图.请根据相关信息,解答下列问题:
(1)图中的值为 ;
(2)统计的这组数据的平均数为 ,众数为 ,中位数为 ;
(3)根据样本数据,估计这枚口罩中,价格为元的约有 枚.
10.某校八年级甲、乙两班各有学生50人,为了解这两个班学生的身体素质情况,进行了抽样调查,过程如下,请补充完整.
⑴收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65 75 75 80 60 50 75 90 85 65
乙班:90 55 80 70 55 70 95 80 65 70
⑵整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x/分
甲班 1 3 3 2 1
乙班 2 1 m 2 n
则 ▲ , ▲ ;
⑶分析数据
①两组样本数据的平均数、中位数、众数如下表:
班级 平均数 中位数 众数
甲班 72 x 75
乙班 73 70 y
则 ▲ , ▲ .
②若规定测试成绩在80分(含80分)以上的学生的身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生人数.
四、综合题
11.校学生会向全校3000名学生发起了“爱心捐助”捐款活动,为了解捐款情况,学生会随机绘制了如图的统计图.请根据相关信息,解答下列问题:
(1)本次接受随机调查的学生人数为 ,图1中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
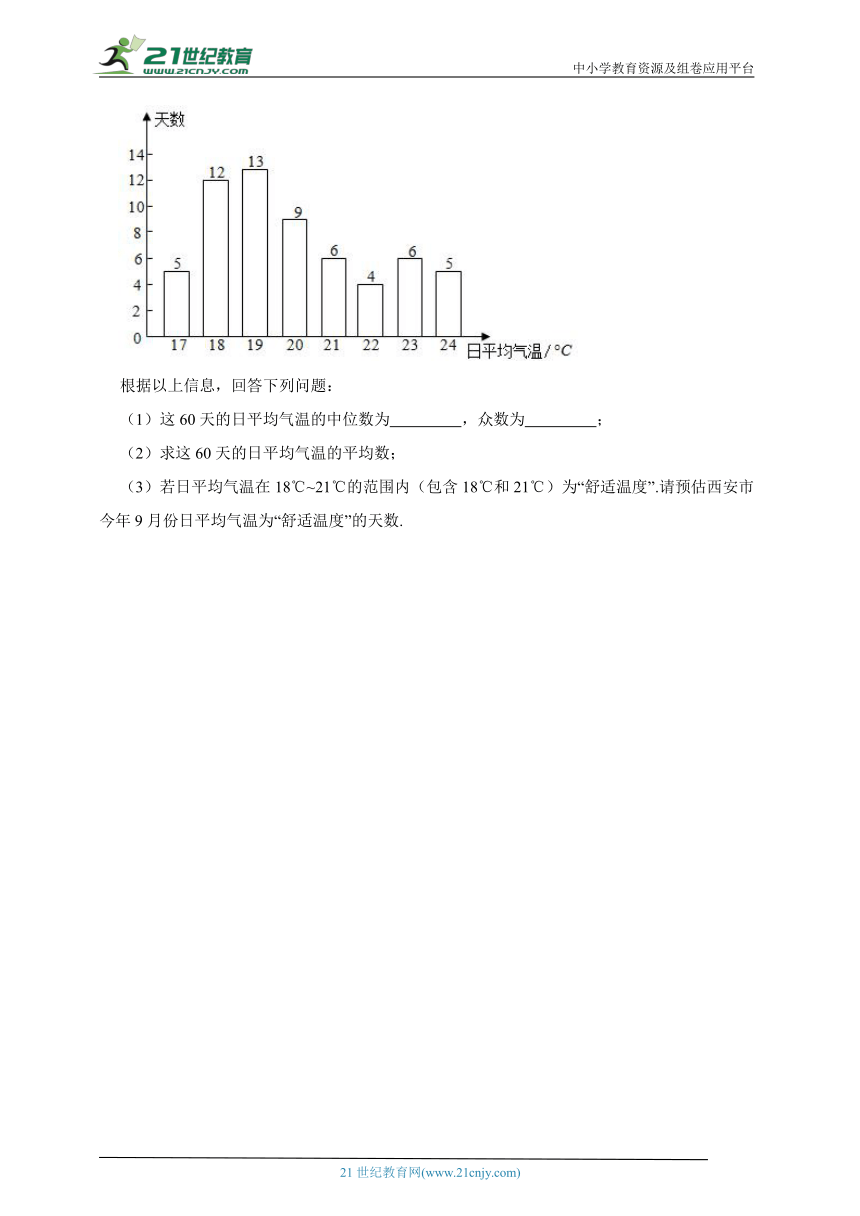
12.今年9月,第十四届全国运动会将在陕西省举行本届全运会主场馆在西安,开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温,从中随机抽取了60天的日平均气温,并绘制成如下统计图:
根据以上信息,回答下列问题:
(1)这60天的日平均气温的中位数为 ,众数为 ;
(2)求这60天的日平均气温的平均数;
(3)若日平均气温在18℃~21℃的范围内(包含18℃和21℃)为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.
答案解析部分
1.【答案】D
【解析】【解答】解:A,平均数为 ,故该选项错误;
B,中位数为0,故该选项错误;
C,所有数据都是出现了1次,所以这组数据没有众数;
D,方差为 ,故该选项正确;
故答案为:D.
【分析】根据平均数,中位数,众数和方差的求法逐一进行判断即可.
2.【答案】C
【解析】【解答】根据题意鞋厂最关注的是众数,
故答案为:C.
【分析】根据众数的定义即可判断.
3.【答案】C
【解析】【解答】解:因为5位获奖者的分数肯定是11名参赛选手中最高的,
而且11个不同的分数按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的分数和中位数就可以知道是否获奖了.
故答案为:C.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
4.【答案】C
【解析】【解答】
0.42<0.56<0.63<0.78
这四人中 ,丙的方差最小,所以成绩最稳定。
故答案为:C
【分析】
方差越小,表明这组数据偏离平均数越小,成绩越稳定,比较四人的方差可得出结果。
5.【答案】乙
【解析】【解答】解:由折线图可知,甲的波动大于乙,
所以乙更稳定,
故答案为:乙.
【分析】本题考查观测折线图,折线图上的波动越小表明越稳定.
6.【答案】丙
【解析】【解答】解:甲和丙的平均成绩都是8.2,比乙和丁都高,但是甲的方差比丙的方差要大,所以丙的成绩更稳定,所以填丙.
故答案为:丙.
【分析】根据甲乙丙丁四人成绩的平均数越大成绩越好,方差越大数据的波动越大即可判断选出适合的人选.
7.【答案】乙
【解析】【解答】解:∵甲、乙两人的平均成绩都是97分,s2甲 ,s2乙 ,
∴s2甲>s2乙,
∴这6次比赛成绩比较稳定的是乙.
故答案为:乙.
【分析】在平均数相同的条件下,方差越小则成绩就越稳定,据此解答即可.
8.【答案】甲
【解析】【解答】解:∵甲、乙两名运动员最近 10 次跳远成绩的平均数均为 402 cm,S甲2 =66.73,S乙2 =85.21,
∴S甲2< S乙2,
∴两名运动员中成绩较稳定的是甲.
故答案为:甲.
【分析】根据方差的意义即方差越小数据越稳定,从而得出答案.
9.【答案】(1)28
(2)1.52元;1.8元;1.5元
(3)200
【解析】【解答】解:(1)∵抽取的样本容量为:5+11+14+16+4=50;
∴m%=14÷50×100%=28%,
即m=28;
故答案为:28.
(2)这组数据的平均数为:=1.52(元);
众数为:1.8元;
中位数为:(元);
故答案为:1.52元,1.8元,1.5元;
(3)2500×8%=200.
故答案为:200.
【分析】(1)由条形图可知每种价格的口罩的频数,根据样本容量等于各小组频数之和可求得样本容量,然后根据百分数等于频数÷样本容量可求得m的值;
(2)根据加权平均数公式计算可求解;
(3)用样本估计总体可求解.
10.【答案】解:⑵3,2.
⑶①75,70.
②根据题意,得(名).
故估计乙班50名学生中身体素质为优秀的学生为20名.
【解析】解:(2)由收集的数据可得:m=_3_,n=_2_;
(3)①将甲班的数据从小到大排列:50,60,65,65,75,75,75,80,85,90,中间的两位数是75,75,这两个数的平均数==75,即x=75;
乙班的数据中,70出现了3次,是出现次数最多的数据,所以乙班的众数是70分,即y=70;
【分析】(2)在收集的数据中找出每一个分数段的数据即可求得m、n的值;
(3)①众数是指一组数据中出现次数最多的数;中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;根据定义并结合收集的数据即可求解;
②用样本估计总体可求解.
11.【答案】(1)50人;32
(2)解:本次调查获取的样本数据的平均数是:
(元),
本次调查获取的样本数据的众数是:10元,
将捐款的金额从小到大进行排序,排在第25和26的都是15元,因此本次调查获取的样本数据的中位数是:(元).
(3)解:估计本次活动捐款金额为10元的学生人数为:3000×=960(人).
【解析】【解答】解:(1)本次接受随机调查的学生人数为4÷8%=50(人),
∴m%=×100%=32%,即m=32.
故答案为:50人;32.
【分析】(1)利用“30元”的人数除以对应的百分比可得总人数,再利用“10元”的人数除以总人数可得答案;
(2)利用平均数、中位数和众数的定义及计算方法求解即可;
(3)先求出“10元”的百分比,再乘以3000可得答案。
12.【答案】(1)19.5;19
(2)解:
,
∴这60天的日平均气温的平均数为20℃
(3)解:∵ ,
∴预估西安市今年9月份日平均气温为“舒适温度”的天数为20天
【解析】【解答】解:(1)由题意得样本共60个数据,故中位数取排序后第30、31个数的中位数,
由统计图得排序后第30个数为19,第31个数为20,
∴中位数为 ,
平均气温19出现的次数最多,
∴众数为19,
故答案为:19.5,19;
【分析】(1)中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;众数是指一组数据中出现次数最多的数;根据定义并结合条形图可求解;
(2)根据加权平均数的计算公式可求解;
(2)用样本估计总体可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
20.3 体质健康测试中的数据分析
一、单选题
1.关于数据3, , ,0,5的说法正确的是( )
A.平均数为 B.中位数为1
C.众数为5 D.方差为6.8
2.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在以下统计量中,该鞋厂最关注的是( )
A.平均数 B.中位数 C.众数 D.方差
3.学校组织才艺表演比赛,前5名获奖.有11位同学参加比赛且他们所得的分数互不相同.某同学知道自己的比赛分数后,要判断自己能否获奖,在这11名同学成绩的统计量中只需知道一个量,它是( )
A.众数 B.方差 C.中位数 D.平均数
4.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩是0.9环.方差分别0.56、0.78、0.42、0.63,这四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
5.如图是甲乙两位同学在参加体育中考前的次体能测试成绩折线统计图,由图可知, 的成绩更稳定.
6.某校射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛,在选拔赛中每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
甲 乙 丙 丁
平均数 8.2 8.0 8.2 8.0
方差 2.0 1.8 1.5 1.6
请你根据表中数据选择其中一人参加比赛,最合适的人选是 .
7.甲、乙两人参加“环保知识”竞赛,经过6轮比赛,他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为 ,则这6次比赛成绩比较稳定的是 .(填“甲”或“乙”)
8.某跳远队甲、乙两名运动员最近 10 次跳远成绩的平均数均为 402 cm,若甲跳远成绩的方差为S甲2 =66.73,乙跳远成绩的方差为S乙2 =85.21,则成绩比较稳定的是 .(填“甲”或“乙”)
三、解答题
9.肃州区某药店有枚口罩准备出售.从中随机抽取了一部分口罩,根据它们的价格单位:元,绘制出如图的统计图.请根据相关信息,解答下列问题:
(1)图中的值为 ;
(2)统计的这组数据的平均数为 ,众数为 ,中位数为 ;
(3)根据样本数据,估计这枚口罩中,价格为元的约有 枚.
10.某校八年级甲、乙两班各有学生50人,为了解这两个班学生的身体素质情况,进行了抽样调查,过程如下,请补充完整.
⑴收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65 75 75 80 60 50 75 90 85 65
乙班:90 55 80 70 55 70 95 80 65 70
⑵整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x/分
甲班 1 3 3 2 1
乙班 2 1 m 2 n
则 ▲ , ▲ ;
⑶分析数据
①两组样本数据的平均数、中位数、众数如下表:
班级 平均数 中位数 众数
甲班 72 x 75
乙班 73 70 y
则 ▲ , ▲ .
②若规定测试成绩在80分(含80分)以上的学生的身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生人数.
四、综合题
11.校学生会向全校3000名学生发起了“爱心捐助”捐款活动,为了解捐款情况,学生会随机绘制了如图的统计图.请根据相关信息,解答下列问题:
(1)本次接受随机调查的学生人数为 ,图1中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
12.今年9月,第十四届全国运动会将在陕西省举行本届全运会主场馆在西安,开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温,从中随机抽取了60天的日平均气温,并绘制成如下统计图:
根据以上信息,回答下列问题:
(1)这60天的日平均气温的中位数为 ,众数为 ;
(2)求这60天的日平均气温的平均数;
(3)若日平均气温在18℃~21℃的范围内(包含18℃和21℃)为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.
答案解析部分
1.【答案】D
【解析】【解答】解:A,平均数为 ,故该选项错误;
B,中位数为0,故该选项错误;
C,所有数据都是出现了1次,所以这组数据没有众数;
D,方差为 ,故该选项正确;
故答案为:D.
【分析】根据平均数,中位数,众数和方差的求法逐一进行判断即可.
2.【答案】C
【解析】【解答】根据题意鞋厂最关注的是众数,
故答案为:C.
【分析】根据众数的定义即可判断.
3.【答案】C
【解析】【解答】解:因为5位获奖者的分数肯定是11名参赛选手中最高的,
而且11个不同的分数按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的分数和中位数就可以知道是否获奖了.
故答案为:C.
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
4.【答案】C
【解析】【解答】
0.42<0.56<0.63<0.78
这四人中 ,丙的方差最小,所以成绩最稳定。
故答案为:C
【分析】
方差越小,表明这组数据偏离平均数越小,成绩越稳定,比较四人的方差可得出结果。
5.【答案】乙
【解析】【解答】解:由折线图可知,甲的波动大于乙,
所以乙更稳定,
故答案为:乙.
【分析】本题考查观测折线图,折线图上的波动越小表明越稳定.
6.【答案】丙
【解析】【解答】解:甲和丙的平均成绩都是8.2,比乙和丁都高,但是甲的方差比丙的方差要大,所以丙的成绩更稳定,所以填丙.
故答案为:丙.
【分析】根据甲乙丙丁四人成绩的平均数越大成绩越好,方差越大数据的波动越大即可判断选出适合的人选.
7.【答案】乙
【解析】【解答】解:∵甲、乙两人的平均成绩都是97分,s2甲 ,s2乙 ,
∴s2甲>s2乙,
∴这6次比赛成绩比较稳定的是乙.
故答案为:乙.
【分析】在平均数相同的条件下,方差越小则成绩就越稳定,据此解答即可.
8.【答案】甲
【解析】【解答】解:∵甲、乙两名运动员最近 10 次跳远成绩的平均数均为 402 cm,S甲2 =66.73,S乙2 =85.21,
∴S甲2< S乙2,
∴两名运动员中成绩较稳定的是甲.
故答案为:甲.
【分析】根据方差的意义即方差越小数据越稳定,从而得出答案.
9.【答案】(1)28
(2)1.52元;1.8元;1.5元
(3)200
【解析】【解答】解:(1)∵抽取的样本容量为:5+11+14+16+4=50;
∴m%=14÷50×100%=28%,
即m=28;
故答案为:28.
(2)这组数据的平均数为:=1.52(元);
众数为:1.8元;
中位数为:(元);
故答案为:1.52元,1.8元,1.5元;
(3)2500×8%=200.
故答案为:200.
【分析】(1)由条形图可知每种价格的口罩的频数,根据样本容量等于各小组频数之和可求得样本容量,然后根据百分数等于频数÷样本容量可求得m的值;
(2)根据加权平均数公式计算可求解;
(3)用样本估计总体可求解.
10.【答案】解:⑵3,2.
⑶①75,70.
②根据题意,得(名).
故估计乙班50名学生中身体素质为优秀的学生为20名.
【解析】解:(2)由收集的数据可得:m=_3_,n=_2_;
(3)①将甲班的数据从小到大排列:50,60,65,65,75,75,75,80,85,90,中间的两位数是75,75,这两个数的平均数==75,即x=75;
乙班的数据中,70出现了3次,是出现次数最多的数据,所以乙班的众数是70分,即y=70;
【分析】(2)在收集的数据中找出每一个分数段的数据即可求得m、n的值;
(3)①众数是指一组数据中出现次数最多的数;中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;根据定义并结合收集的数据即可求解;
②用样本估计总体可求解.
11.【答案】(1)50人;32
(2)解:本次调查获取的样本数据的平均数是:
(元),
本次调查获取的样本数据的众数是:10元,
将捐款的金额从小到大进行排序,排在第25和26的都是15元,因此本次调查获取的样本数据的中位数是:(元).
(3)解:估计本次活动捐款金额为10元的学生人数为:3000×=960(人).
【解析】【解答】解:(1)本次接受随机调查的学生人数为4÷8%=50(人),
∴m%=×100%=32%,即m=32.
故答案为:50人;32.
【分析】(1)利用“30元”的人数除以对应的百分比可得总人数,再利用“10元”的人数除以总人数可得答案;
(2)利用平均数、中位数和众数的定义及计算方法求解即可;
(3)先求出“10元”的百分比,再乘以3000可得答案。
12.【答案】(1)19.5;19
(2)解:
,
∴这60天的日平均气温的平均数为20℃
(3)解:∵ ,
∴预估西安市今年9月份日平均气温为“舒适温度”的天数为20天
【解析】【解答】解:(1)由题意得样本共60个数据,故中位数取排序后第30、31个数的中位数,
由统计图得排序后第30个数为19,第31个数为20,
∴中位数为 ,
平均气温19出现的次数最多,
∴众数为19,
故答案为:19.5,19;
【分析】(1)中位数是指一组数据按序排列后①偶数个数据时,中间两个数的平均数就是这组数据的中位数;②奇数个数据时,中间的数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;众数是指一组数据中出现次数最多的数;根据定义并结合条形图可求解;
(2)根据加权平均数的计算公式可求解;
(2)用样本估计总体可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
