8.4 平行线的判定定理同步练习题(含答案)
文档属性
| 名称 | 8.4 平行线的判定定理同步练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 14.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览


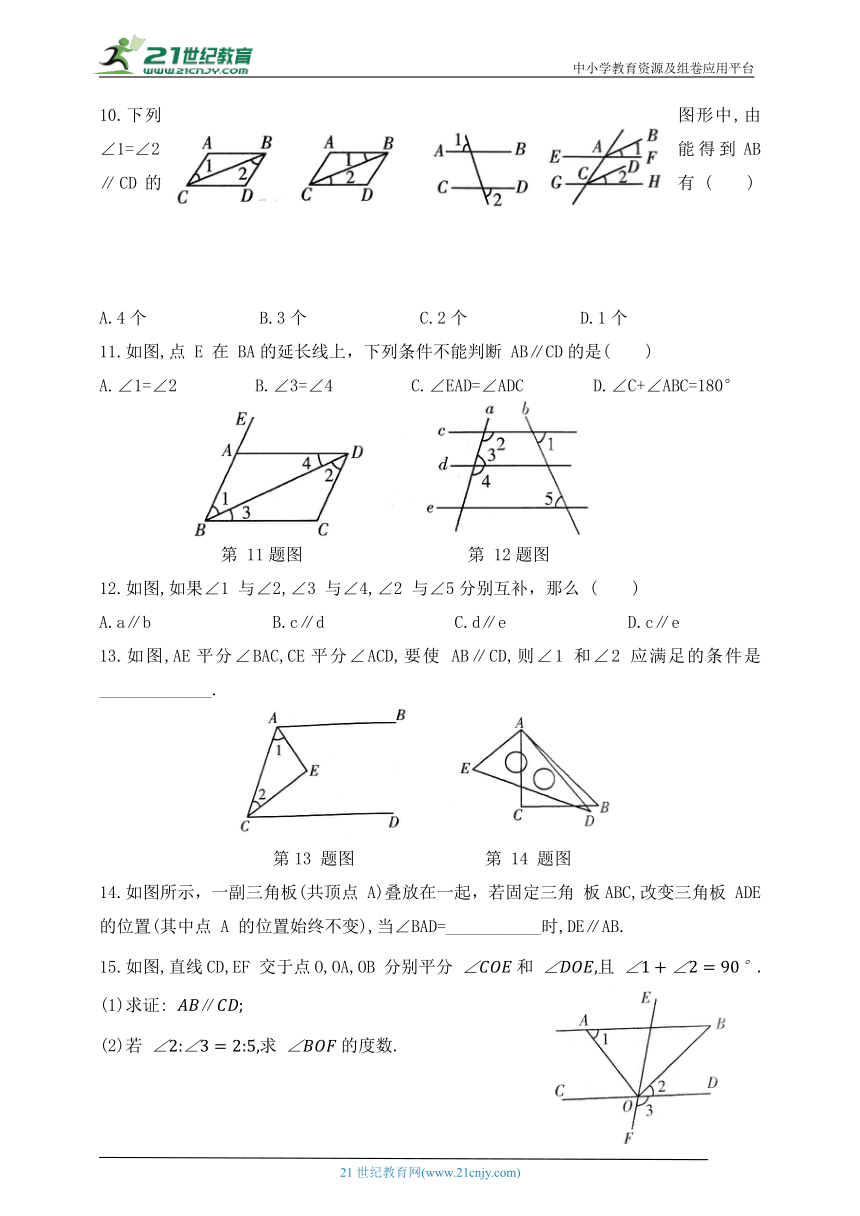
文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
4 平行线的判定定理
基 础 练
知识点一 同位角相等,两直线平行
1.如图,将木条a,b与c(木条看作直线)钉在一起, 若要使木条a 与b平行,则∠1 的度数应为 ( )
A.40° B.50° C.90°
第1 题图 第 2 题图
2.如图,用直尺和三角尺作出直线 AB,CD,得到 的理由是__________.
3.已知:如图,直线 AB 与CD 被 EF 所截, 求证: ∥
知识点二 内错角相等,两直线平行
4.如图,下列条件中可以判定 ∥的是 ( )
第4题图 第5题图
5.如图,小明在两块按如图所示的方式摆放的含 角的直角三角板的边缘画直线 AB,CD,得到 ∥这是根据________________,两直线平行.
6.如图,已知 试判断 BE与CF的关系,并说明你的理由.
知识点三 同旁内角互补,两直线平行
7.如图,下列条件中能判定直线 ∥的是 ( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
第7题图 第8题图
8.如图,直线 a,b被直线 c 所截, 当 时, ∥
9.如图,若 试说明EF∥BC.
提 升 练
10.下列图形中,由∠1=∠2能得到AB∥CD的有 ( )
A.4个 B.3个 C.2个 D.1个
11.如图,点 E 在 BA的延长线上,下列条件不能判断 AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠EAD=∠ADC D.∠C+∠ABC=180°
第 11题图 第 12题图
12.如图,如果∠1 与∠2,∠3 与∠4,∠2 与∠5分别互补,那么 ( )
A.a∥b B.c∥d C.d∥e D.c∥e
13.如图,AE平分∠BAC,CE平分∠ACD,要使 AB∥CD,则∠1 和∠2 应满足的条件是_____________.
第13 题图 第 14 题图
14.如图所示,一副三角板(共顶点 A)叠放在一起,若固定三角 板ABC,改变三角板 ADE的位置(其中点 A 的位置始终不变),当∠BAD=___________时,DE∥AB.
15.如图,直线CD,EF 交于点O,OA,OB 分别平分 和 且
(1)求证: ∥
(2)若 求 的度数.
16.如图,台球运动中母球 P 击中桌边的点A,经桌边反弹后击中相邻的另一桌边的点 B,再次反弹经过点C(提示:∠PAD=∠BAE,∠ABE=∠CBF).
(1)若∠PAD=32°,求∠PAB的度数;
(2)已知∠BAE+∠ABE=90°,母球 P 经过的路线 BC与PA一定平行吗 请说明理由.
参考答案
1. B
2.同位角相等,两直线平行
3.证明:∵∠2=∠3(对顶角相等),∠1=∠2(已知),∴∠1=∠3,
∴AB∥CD(同位角相等,两直线平行).
4. D
5.内错角相等
6.解:BE∥CF.理由如下:
因为 AB⊥BC,BC⊥CD,所以∠ABC=∠BCD=90°.
因为∠1=∠2,所以∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF,
所以 BE∥CF(内错角相等,两直线平行).
7. C 8.50
9.证明:∵∠EAD=∠FAB,∠EAD=130°,∴∠FAB=130°.
∵∠B=50°,∴∠B+∠FAB=180°,∴EF∥BC.
10. C 11. B 12. D 13.∠1+∠2=90° 14.30°或150°
15.(1)证明:∵OA,OB 分别平分∠COE 和∠DOE,
∠DOE.
又∵∠COE+∠DOE=180°,∴∠2+∠AOC=90°.
∵∠1+∠2=90°,∴∠1=∠AOC,
∴AB∥CD(内错角相等,两直线平行).
(2)解:
由(1)知,∠2+∠AOC=90°,
∴∠2=40°,∴∠3=100°.∴∠BOF=∠2+∠3=140°.
16.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°-32°-32°=116°.
(2)BC∥PA.
理由如下:∵∠PAD=∠BAE,∠PAB=180°-∠PAD-∠BAE,
∴∠PAB=180°-2∠BAE.
同理可得∠ABC=180°-2∠ABE.
∵∠BAE+∠ABE=90°,∴∠PAB+∠ABC=360°-2(∠BAE+∠ABE)=180°.
∴BC∥PA(同旁内角互补,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
4 平行线的判定定理
基 础 练
知识点一 同位角相等,两直线平行
1.如图,将木条a,b与c(木条看作直线)钉在一起, 若要使木条a 与b平行,则∠1 的度数应为 ( )
A.40° B.50° C.90°
第1 题图 第 2 题图
2.如图,用直尺和三角尺作出直线 AB,CD,得到 的理由是__________.
3.已知:如图,直线 AB 与CD 被 EF 所截, 求证: ∥
知识点二 内错角相等,两直线平行
4.如图,下列条件中可以判定 ∥的是 ( )
第4题图 第5题图
5.如图,小明在两块按如图所示的方式摆放的含 角的直角三角板的边缘画直线 AB,CD,得到 ∥这是根据________________,两直线平行.
6.如图,已知 试判断 BE与CF的关系,并说明你的理由.
知识点三 同旁内角互补,两直线平行
7.如图,下列条件中能判定直线 ∥的是 ( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
第7题图 第8题图
8.如图,直线 a,b被直线 c 所截, 当 时, ∥
9.如图,若 试说明EF∥BC.
提 升 练
10.下列图形中,由∠1=∠2能得到AB∥CD的有 ( )
A.4个 B.3个 C.2个 D.1个
11.如图,点 E 在 BA的延长线上,下列条件不能判断 AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠EAD=∠ADC D.∠C+∠ABC=180°
第 11题图 第 12题图
12.如图,如果∠1 与∠2,∠3 与∠4,∠2 与∠5分别互补,那么 ( )
A.a∥b B.c∥d C.d∥e D.c∥e
13.如图,AE平分∠BAC,CE平分∠ACD,要使 AB∥CD,则∠1 和∠2 应满足的条件是_____________.
第13 题图 第 14 题图
14.如图所示,一副三角板(共顶点 A)叠放在一起,若固定三角 板ABC,改变三角板 ADE的位置(其中点 A 的位置始终不变),当∠BAD=___________时,DE∥AB.
15.如图,直线CD,EF 交于点O,OA,OB 分别平分 和 且
(1)求证: ∥
(2)若 求 的度数.
16.如图,台球运动中母球 P 击中桌边的点A,经桌边反弹后击中相邻的另一桌边的点 B,再次反弹经过点C(提示:∠PAD=∠BAE,∠ABE=∠CBF).
(1)若∠PAD=32°,求∠PAB的度数;
(2)已知∠BAE+∠ABE=90°,母球 P 经过的路线 BC与PA一定平行吗 请说明理由.
参考答案
1. B
2.同位角相等,两直线平行
3.证明:∵∠2=∠3(对顶角相等),∠1=∠2(已知),∴∠1=∠3,
∴AB∥CD(同位角相等,两直线平行).
4. D
5.内错角相等
6.解:BE∥CF.理由如下:
因为 AB⊥BC,BC⊥CD,所以∠ABC=∠BCD=90°.
因为∠1=∠2,所以∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF,
所以 BE∥CF(内错角相等,两直线平行).
7. C 8.50
9.证明:∵∠EAD=∠FAB,∠EAD=130°,∴∠FAB=130°.
∵∠B=50°,∴∠B+∠FAB=180°,∴EF∥BC.
10. C 11. B 12. D 13.∠1+∠2=90° 14.30°或150°
15.(1)证明:∵OA,OB 分别平分∠COE 和∠DOE,
∠DOE.
又∵∠COE+∠DOE=180°,∴∠2+∠AOC=90°.
∵∠1+∠2=90°,∴∠1=∠AOC,
∴AB∥CD(内错角相等,两直线平行).
(2)解:
由(1)知,∠2+∠AOC=90°,
∴∠2=40°,∴∠3=100°.∴∠BOF=∠2+∠3=140°.
16.解:(1)∵∠PAD=32°,∠PAD=∠BAE,∠PAD+∠PAB+∠BAE=180°,
∴∠PAB=180°-32°-32°=116°.
(2)BC∥PA.
理由如下:∵∠PAD=∠BAE,∠PAB=180°-∠PAD-∠BAE,
∴∠PAB=180°-2∠BAE.
同理可得∠ABC=180°-2∠ABE.
∵∠BAE+∠ABE=90°,∴∠PAB+∠ABC=360°-2(∠BAE+∠ABE)=180°.
∴BC∥PA(同旁内角互补,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
