第五、六章综合练习 (含答案)人教版七年级数学下册
文档属性
| 名称 | 第五、六章综合练习 (含答案)人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 357.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 17:39:22 | ||
图片预览



文档简介
第五、六章综合练习2023-2024学年人教版七年级数学下册
一.选择题(共12小题)
1.下列四个实数中,是无理数的是( )
A.3 B. C. D.0
2.在实数,0,﹣0.3,3.1415926,4,﹣2022,π中,有理数的个数为( )
A.3 B.4 C.5 D.6
3.16的算术平方根是( )
A.﹣4 B.4 C.8 D.﹣8
4.运动会上,跳远运动员跳落到沙坑时的痕迹和测量跳远成绩的方法如图所示,选择其中的③号线的长度作为跳远成绩,这样测量的依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.平行线之间的距离处处相等
5.平方根等于它本身的数是( )
A.﹣1 B.0 C.1 D.±1
6.如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76° C.84° D.86°
7.如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=50°,则∠BOE等于( )
A.65° B.60° C.50° D.45°
8.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠EFC的度数是( )
A.60° B.65° C.70° D.75°
9.规定新运算“*”:对于任意实数a、b都有a*b=ab2﹣a﹣b2,例如:2*5=2×52﹣2﹣52=23,若(1﹣2x)*3=15,则x的值为( )
A. B. C.﹣1 D.1
10.如图,AC⊥BC,垂足为C,AC=6,BC=8,AB=10.P是线段AB上一点,连接PC,PC的长不可能是( )
A.4 B.5 C.6 D.7
11.如图,AC⊥BC,CD⊥AB,垂足分别为C,D.下列说法正确的个数是( )
①点C到线段AB的距离为线段CD的长度;
②∠ACD+∠B=90°;
③∠A=∠BCD;
④将三角形ABC绕线段BC所在直线旋转一周得到的几何体是圆锥.
A.1个 B.2个 C.3个 D.4个
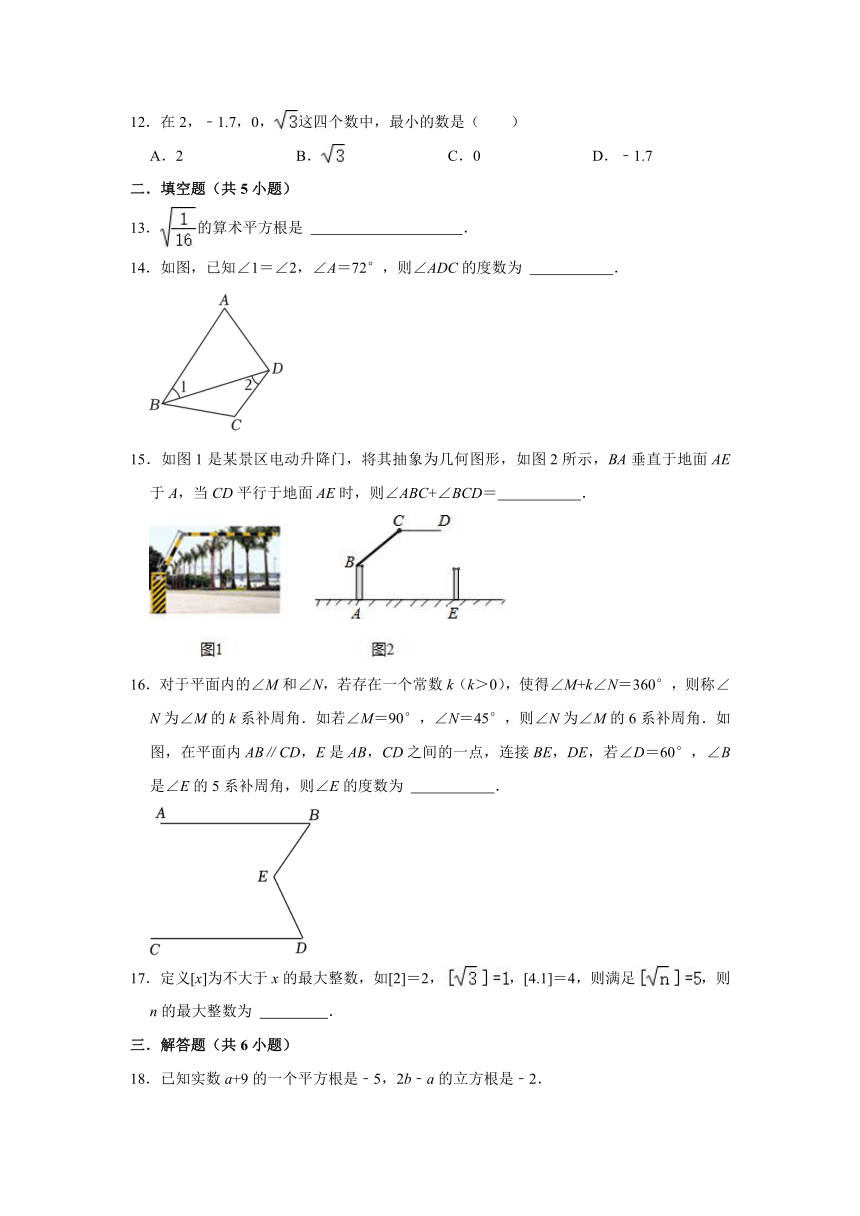
12.在2,﹣1.7,0,这四个数中,最小的数是( )
A.2 B. C.0 D.﹣1.7
二.填空题(共5小题)
13.的算术平方根是 .
14.如图,已知∠1=∠2,∠A=72°,则∠ADC的度数为 .
15.如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD= .
16.对于平面内的∠M和∠N,若存在一个常数k(k>0),使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.如图,在平面内AB∥CD,E是AB,CD之间的一点,连接BE,DE,若∠D=60°,∠B是∠E的5系补周角,则∠E的度数为 .
17.定义[x]为不大于x的最大整数,如[2]=2,,[4.1]=4,则满足,则n的最大整数为 .
三.解答题(共6小题)
18.已知实数a+9的一个平方根是﹣5,2b﹣a的立方根是﹣2.
(1)求a、b的值.
(2)求2a+b的算术平方根.
19.计算:
(1)﹣2+3+(﹣14);
(2).
(3)﹣3+1﹣(﹣1);
(4).
20.请完成下面的证明.
如图,∠ABC=∠ADC,BF,DE分别平分∠ABC,∠ADC,且∠1=∠3,求证:∠1+∠4=180°.
证明:∵BF,DE分别平分∠ABC,∠ADC,
∴∠1=∠ABC,∠2= ( ),
∵∠ABC=∠ADC,
∴∠1=∠2.
∵∠1=∠3,
∴∠2= ( ),
∴AB∥CD( ),
∴∠1+∠4=180° ( ).
21.如图1,直角三角板ABC(∠ABC=30°)的直角边AC所在直线与直线MN重合.将该三角板绕点A逆时针旋转一定角度后,如图2所示.记∠CAN=∠α(0°<∠α<90°),过B作直线DE∥MN.P为射线AM上异于点A的一点,从点P出发且位于直线MN上方的射线交直线AB于点Q,记∠NPQ=∠β(0°<∠β<∠α+60°).
(1)若∠CBE=30°,且PQ∥AC,求∠β的度数;
(2)①若点Q在线段AB上(不含端点),则∠BQP与∠α,∠β满足的数量关系为 ;
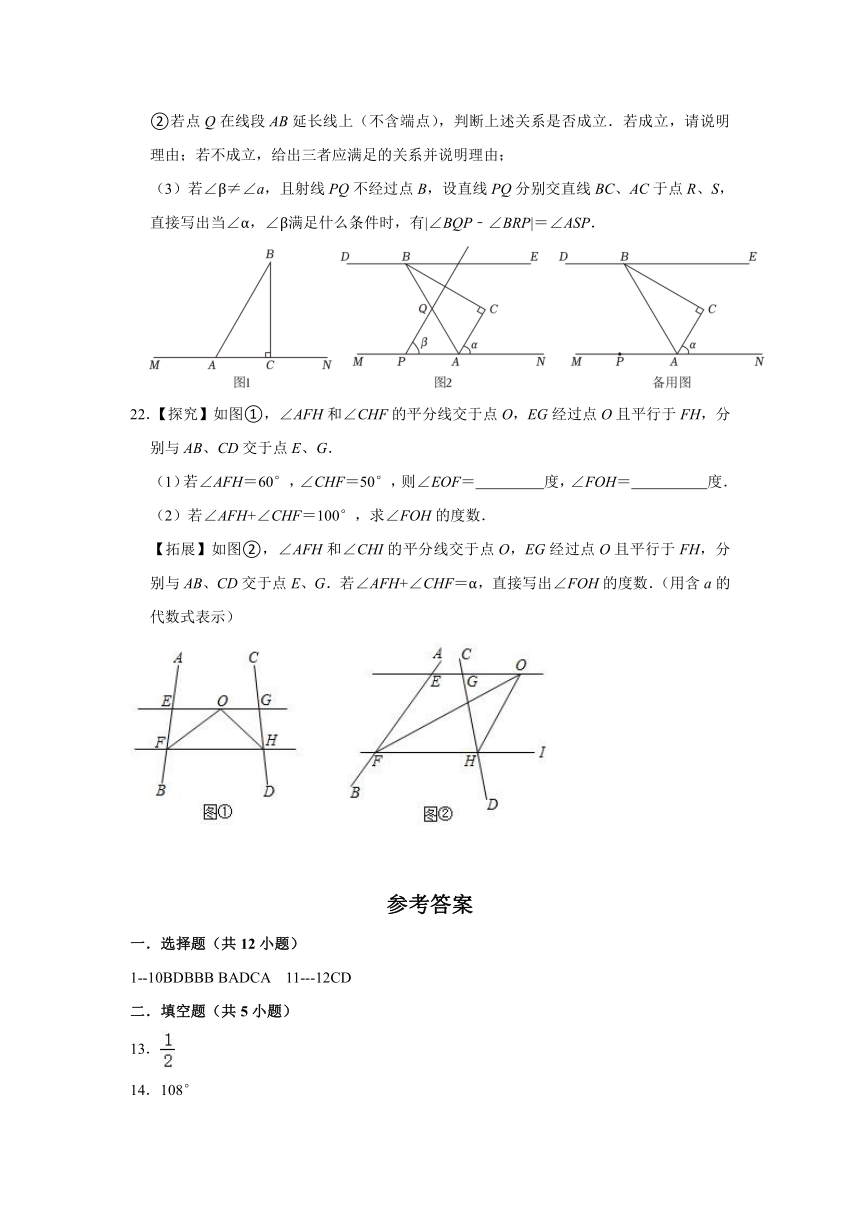
②若点Q在线段AB延长线上(不含端点),判断上述关系是否成立.若成立,请说明理由;若不成立,给出三者应满足的关系并说明理由;
(3)若∠β≠∠a,且射线PQ不经过点B,设直线PQ分别交直线BC、AC于点R、S,直接写出当∠α,∠β满足什么条件时,有|∠BQP﹣∠BRP|=∠ASP.
22.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= 度,∠FOH= 度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
参考答案
一.选择题(共12小题)
1--10BDBBB BADCA 11---12CD
二.填空题(共5小题)
13.
14.108°
15.270°
16.110°
17.35
三.解答题(共6小题)
18.解:(1)∵实数a+9的一个平方根是﹣5,
∴a+9=(﹣5)2=25,
解得a=16,
∵2b﹣a的立方根是﹣2,
∴2b﹣a=(﹣2)3=﹣8,即2b﹣16=﹣8,
解得b=4,
∴a=16,b=4;
(2)解:,
即2a+b的算术平方根是6.
19.解:(1)﹣2+3+(﹣14)
=﹣2+3﹣14
=﹣13;
(2)
=4+4÷2
=4+2
=6.
(3)原式=﹣3+1+1
=1+1﹣3
=2﹣3
=﹣1;
(4)原式=5﹣27÷9
=5﹣3
=2.
20.解:∵BF,DE分别平分∠ABC,∠ADC,
∴∠1=∠ABC,∠2=∠ADC(角平分线的定义),
∵∠ABC=∠ADC,
∴∠1=∠2.
∵∠1=∠3,
∴∠2=∠3(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠1+∠4=180°(两直线平行,同旁内角互补),
故答案为:∠ADC;角平分线的定义;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
21.解:(1)过点C作CT∥DE,如图2所示:
∵DE∥MN,
∴DE∥CT∥MN,
∴∠TCB=∠CBE=30°,∠TCA=∠CAN=∠α,
∴∠ACB=∠TCB+∠TCA=30°+∠α,
∵∠ACB=90°,
∴30°+∠α=90°,
∴∠α=60°,
∵PQ∥AC,
∴∠β=∠α=60°;
(2)①∵∠ABC=30°,∠ACB=90°,
∴∠BAC=60°,
∴∠QAN=∠BAC+∠CAN=60°+∠α,
∵∠QAP=180°﹣∠QAN=180°﹣(60°+∠α)=120°﹣∠α,
∴∠BQP=∠QAP+∠NPQ=120°﹣∠α+∠β,
∴∠BQP与∠α,∠β满足的数量关系为:∠BQP=120°﹣∠α+∠β;
故答案为:∠BQP=120°﹣∠α+∠β.
②若点Q在线段AB延长线上(不含端点),上述关系不成立,三者满足的关系是:∠BQP=60°+∠α﹣∠β,
理由如下:
过点Q作QH∥DE,如图3所示:
∵DE∥MN,
∴QH∥DE∥MN,
∴∠HQA=∠QAP=120°﹣∠α,
∠HQP=180°﹣∠QPN=180°﹣∠β,
∴∠BQP=∠HQP﹣∠HQA=180°﹣∠β﹣(120°﹣∠α)=60°+∠α﹣∠β,
即∠BQP=60°+∠α﹣∠β;
(3)依题意有以下四种情况:
①当PQ与线段BC交于R,与AC的延长线于S时,如图4所示:
∵∠QAP=120°﹣∠α,
∴∠BQP=∠QPA+∠QAP=∠β+120°﹣∠α,
∵∠CAN=∠QPA+∠ASP,
∴∠ASP=∠CAN﹣∠QPA=∠α﹣∠β,
∵∠BRP=∠SRC=90°﹣∠ASP=90°﹣(∠α﹣∠β)=90°﹣∠α+∠β,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°﹣∠α+∠β)|=∠α﹣∠β,
整理得:∠α﹣∠β=30°,
∴当∠α﹣∠β=30°时,有|∠BQP﹣∠BRP|=∠ASP;
②当PQ与线段AC交于S,与BC的延长线交于R时,如图5所示:
同理得:∠BQP=∠β+120°﹣∠α,∠ASP=∠α﹣∠β,
∴∠BRP=90°﹣∠CSR=90°﹣∠ASP=90°﹣(∠α﹣∠β)=90°﹣∠α+∠β,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°﹣∠α+∠β)|=∠α﹣∠β,
整理得:∠α﹣∠β=30°,
∴当∠α﹣∠β=30°时,有|∠BQP﹣∠BRP|=∠ASP;
③当PQ与线段BC交于R,与CA的延长线交于S时,如图6所示:
同理得:∠BQP=∠β+120°﹣∠α,
∵∠QPA=∠ASP+∠PAS=∠ASP+∠CAN,
∴∠ASP=∠QPA﹣∠CAN=∠β﹣∠α,
∴∠BRP=90°+∠ASP=90°+∠β﹣∠α,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°+∠β﹣∠α)|=∠β﹣∠α,
整理得:∠β﹣∠α=30°,
∴当∠β﹣∠α=30°,有|∠BQP﹣∠BRP|=∠ASP;
④当PQ与AB的延长线交于Q,与CB的延长线交于R,与CA的延长线交于S时,如图7所示:
同理得:∠ASP=∠β﹣∠α,
∴∠BQP=180°﹣∠BAP﹣∠QPA=180°﹣(120°﹣∠α)﹣∠β=60°+∠α﹣∠β,
∴∠BRP=90°﹣∠ASP=90°﹣(∠β﹣∠α)=90°﹣∠β+∠α,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|60°+∠α﹣∠β﹣(90°﹣∠β+∠α)|=∠β﹣∠α,
整理得:∠β﹣∠α=30°,
∴当∠β﹣∠α=30°,有|∠BQP﹣∠BRP|=∠ASP,
综上所述:当|∠α﹣∠β|=30°时,有|∠BQP﹣∠BRP|=∠ASP.
22.解:【探究】(1)∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°﹣∠OFH﹣∠OHF=125°;
故答案为:30,125;
(2)∵FO平分∠AFH,HO平分∠CHF,
∴∠OFH=∠AFH,∠OHF=∠CHF.
∵∠AFH+∠CHF=100°,
∴∠OFH+∠OHF=(∠AFH+∠CHF)=×100°=50°.
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
∴∠FOH=180°﹣(∠EOF+∠GOH )=180°﹣50°=130°.
【拓展】∵∠AFH和∠CHI的平分线交于点O,
∴∠OFH=∠AFH,∠OHI=∠CHI,
∴∠FOH=∠OHI﹣∠OFH
=(∠CHI﹣∠AFH)
=(180°﹣∠CHF﹣∠AFH)
=(180°﹣α)
=90°﹣α.
一.选择题(共12小题)
1.下列四个实数中,是无理数的是( )
A.3 B. C. D.0
2.在实数,0,﹣0.3,3.1415926,4,﹣2022,π中,有理数的个数为( )
A.3 B.4 C.5 D.6
3.16的算术平方根是( )
A.﹣4 B.4 C.8 D.﹣8
4.运动会上,跳远运动员跳落到沙坑时的痕迹和测量跳远成绩的方法如图所示,选择其中的③号线的长度作为跳远成绩,这样测量的依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.平行线之间的距离处处相等
5.平方根等于它本身的数是( )
A.﹣1 B.0 C.1 D.±1
6.如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76° C.84° D.86°
7.如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=50°,则∠BOE等于( )
A.65° B.60° C.50° D.45°
8.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠EFC的度数是( )
A.60° B.65° C.70° D.75°
9.规定新运算“*”:对于任意实数a、b都有a*b=ab2﹣a﹣b2,例如:2*5=2×52﹣2﹣52=23,若(1﹣2x)*3=15,则x的值为( )
A. B. C.﹣1 D.1
10.如图,AC⊥BC,垂足为C,AC=6,BC=8,AB=10.P是线段AB上一点,连接PC,PC的长不可能是( )
A.4 B.5 C.6 D.7
11.如图,AC⊥BC,CD⊥AB,垂足分别为C,D.下列说法正确的个数是( )
①点C到线段AB的距离为线段CD的长度;
②∠ACD+∠B=90°;
③∠A=∠BCD;
④将三角形ABC绕线段BC所在直线旋转一周得到的几何体是圆锥.
A.1个 B.2个 C.3个 D.4个
12.在2,﹣1.7,0,这四个数中,最小的数是( )
A.2 B. C.0 D.﹣1.7
二.填空题(共5小题)
13.的算术平方根是 .
14.如图,已知∠1=∠2,∠A=72°,则∠ADC的度数为 .
15.如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD= .
16.对于平面内的∠M和∠N,若存在一个常数k(k>0),使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.如图,在平面内AB∥CD,E是AB,CD之间的一点,连接BE,DE,若∠D=60°,∠B是∠E的5系补周角,则∠E的度数为 .
17.定义[x]为不大于x的最大整数,如[2]=2,,[4.1]=4,则满足,则n的最大整数为 .
三.解答题(共6小题)
18.已知实数a+9的一个平方根是﹣5,2b﹣a的立方根是﹣2.
(1)求a、b的值.
(2)求2a+b的算术平方根.
19.计算:
(1)﹣2+3+(﹣14);
(2).
(3)﹣3+1﹣(﹣1);
(4).
20.请完成下面的证明.
如图,∠ABC=∠ADC,BF,DE分别平分∠ABC,∠ADC,且∠1=∠3,求证:∠1+∠4=180°.
证明:∵BF,DE分别平分∠ABC,∠ADC,
∴∠1=∠ABC,∠2= ( ),
∵∠ABC=∠ADC,
∴∠1=∠2.
∵∠1=∠3,
∴∠2= ( ),
∴AB∥CD( ),
∴∠1+∠4=180° ( ).
21.如图1,直角三角板ABC(∠ABC=30°)的直角边AC所在直线与直线MN重合.将该三角板绕点A逆时针旋转一定角度后,如图2所示.记∠CAN=∠α(0°<∠α<90°),过B作直线DE∥MN.P为射线AM上异于点A的一点,从点P出发且位于直线MN上方的射线交直线AB于点Q,记∠NPQ=∠β(0°<∠β<∠α+60°).
(1)若∠CBE=30°,且PQ∥AC,求∠β的度数;
(2)①若点Q在线段AB上(不含端点),则∠BQP与∠α,∠β满足的数量关系为 ;
②若点Q在线段AB延长线上(不含端点),判断上述关系是否成立.若成立,请说明理由;若不成立,给出三者应满足的关系并说明理由;
(3)若∠β≠∠a,且射线PQ不经过点B,设直线PQ分别交直线BC、AC于点R、S,直接写出当∠α,∠β满足什么条件时,有|∠BQP﹣∠BRP|=∠ASP.
22.【探究】如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= 度,∠FOH= 度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
【拓展】如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)
参考答案
一.选择题(共12小题)
1--10BDBBB BADCA 11---12CD
二.填空题(共5小题)
13.
14.108°
15.270°
16.110°
17.35
三.解答题(共6小题)
18.解:(1)∵实数a+9的一个平方根是﹣5,
∴a+9=(﹣5)2=25,
解得a=16,
∵2b﹣a的立方根是﹣2,
∴2b﹣a=(﹣2)3=﹣8,即2b﹣16=﹣8,
解得b=4,
∴a=16,b=4;
(2)解:,
即2a+b的算术平方根是6.
19.解:(1)﹣2+3+(﹣14)
=﹣2+3﹣14
=﹣13;
(2)
=4+4÷2
=4+2
=6.
(3)原式=﹣3+1+1
=1+1﹣3
=2﹣3
=﹣1;
(4)原式=5﹣27÷9
=5﹣3
=2.
20.解:∵BF,DE分别平分∠ABC,∠ADC,
∴∠1=∠ABC,∠2=∠ADC(角平分线的定义),
∵∠ABC=∠ADC,
∴∠1=∠2.
∵∠1=∠3,
∴∠2=∠3(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠1+∠4=180°(两直线平行,同旁内角互补),
故答案为:∠ADC;角平分线的定义;∠3;等量代换;内错角相等,两直线平行;两直线平行,同旁内角互补.
21.解:(1)过点C作CT∥DE,如图2所示:
∵DE∥MN,
∴DE∥CT∥MN,
∴∠TCB=∠CBE=30°,∠TCA=∠CAN=∠α,
∴∠ACB=∠TCB+∠TCA=30°+∠α,
∵∠ACB=90°,
∴30°+∠α=90°,
∴∠α=60°,
∵PQ∥AC,
∴∠β=∠α=60°;
(2)①∵∠ABC=30°,∠ACB=90°,
∴∠BAC=60°,
∴∠QAN=∠BAC+∠CAN=60°+∠α,
∵∠QAP=180°﹣∠QAN=180°﹣(60°+∠α)=120°﹣∠α,
∴∠BQP=∠QAP+∠NPQ=120°﹣∠α+∠β,
∴∠BQP与∠α,∠β满足的数量关系为:∠BQP=120°﹣∠α+∠β;
故答案为:∠BQP=120°﹣∠α+∠β.
②若点Q在线段AB延长线上(不含端点),上述关系不成立,三者满足的关系是:∠BQP=60°+∠α﹣∠β,
理由如下:
过点Q作QH∥DE,如图3所示:
∵DE∥MN,
∴QH∥DE∥MN,
∴∠HQA=∠QAP=120°﹣∠α,
∠HQP=180°﹣∠QPN=180°﹣∠β,
∴∠BQP=∠HQP﹣∠HQA=180°﹣∠β﹣(120°﹣∠α)=60°+∠α﹣∠β,
即∠BQP=60°+∠α﹣∠β;
(3)依题意有以下四种情况:
①当PQ与线段BC交于R,与AC的延长线于S时,如图4所示:
∵∠QAP=120°﹣∠α,
∴∠BQP=∠QPA+∠QAP=∠β+120°﹣∠α,
∵∠CAN=∠QPA+∠ASP,
∴∠ASP=∠CAN﹣∠QPA=∠α﹣∠β,
∵∠BRP=∠SRC=90°﹣∠ASP=90°﹣(∠α﹣∠β)=90°﹣∠α+∠β,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°﹣∠α+∠β)|=∠α﹣∠β,
整理得:∠α﹣∠β=30°,
∴当∠α﹣∠β=30°时,有|∠BQP﹣∠BRP|=∠ASP;
②当PQ与线段AC交于S,与BC的延长线交于R时,如图5所示:
同理得:∠BQP=∠β+120°﹣∠α,∠ASP=∠α﹣∠β,
∴∠BRP=90°﹣∠CSR=90°﹣∠ASP=90°﹣(∠α﹣∠β)=90°﹣∠α+∠β,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°﹣∠α+∠β)|=∠α﹣∠β,
整理得:∠α﹣∠β=30°,
∴当∠α﹣∠β=30°时,有|∠BQP﹣∠BRP|=∠ASP;
③当PQ与线段BC交于R,与CA的延长线交于S时,如图6所示:
同理得:∠BQP=∠β+120°﹣∠α,
∵∠QPA=∠ASP+∠PAS=∠ASP+∠CAN,
∴∠ASP=∠QPA﹣∠CAN=∠β﹣∠α,
∴∠BRP=90°+∠ASP=90°+∠β﹣∠α,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|∠β+120°﹣∠α﹣(90°+∠β﹣∠α)|=∠β﹣∠α,
整理得:∠β﹣∠α=30°,
∴当∠β﹣∠α=30°,有|∠BQP﹣∠BRP|=∠ASP;
④当PQ与AB的延长线交于Q,与CB的延长线交于R,与CA的延长线交于S时,如图7所示:
同理得:∠ASP=∠β﹣∠α,
∴∠BQP=180°﹣∠BAP﹣∠QPA=180°﹣(120°﹣∠α)﹣∠β=60°+∠α﹣∠β,
∴∠BRP=90°﹣∠ASP=90°﹣(∠β﹣∠α)=90°﹣∠β+∠α,
∵|∠BQP﹣∠BRP|=∠ASP,
∴|60°+∠α﹣∠β﹣(90°﹣∠β+∠α)|=∠β﹣∠α,
整理得:∠β﹣∠α=30°,
∴当∠β﹣∠α=30°,有|∠BQP﹣∠BRP|=∠ASP,
综上所述:当|∠α﹣∠β|=30°时,有|∠BQP﹣∠BRP|=∠ASP.
22.解:【探究】(1)∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°﹣∠OFH﹣∠OHF=125°;
故答案为:30,125;
(2)∵FO平分∠AFH,HO平分∠CHF,
∴∠OFH=∠AFH,∠OHF=∠CHF.
∵∠AFH+∠CHF=100°,
∴∠OFH+∠OHF=(∠AFH+∠CHF)=×100°=50°.
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
∴∠FOH=180°﹣(∠EOF+∠GOH )=180°﹣50°=130°.
【拓展】∵∠AFH和∠CHI的平分线交于点O,
∴∠OFH=∠AFH,∠OHI=∠CHI,
∴∠FOH=∠OHI﹣∠OFH
=(∠CHI﹣∠AFH)
=(180°﹣∠CHF﹣∠AFH)
=(180°﹣α)
=90°﹣α.
