六年级下册数学人教版奥数专讲:表面积与体积(课件)(共18张PPT)
文档属性
| 名称 | 六年级下册数学人教版奥数专讲:表面积与体积(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 13:11:44 | ||
图片预览



文档简介
(共18张PPT)
第12讲:表面积与体积
奥数六年级下册春季课程
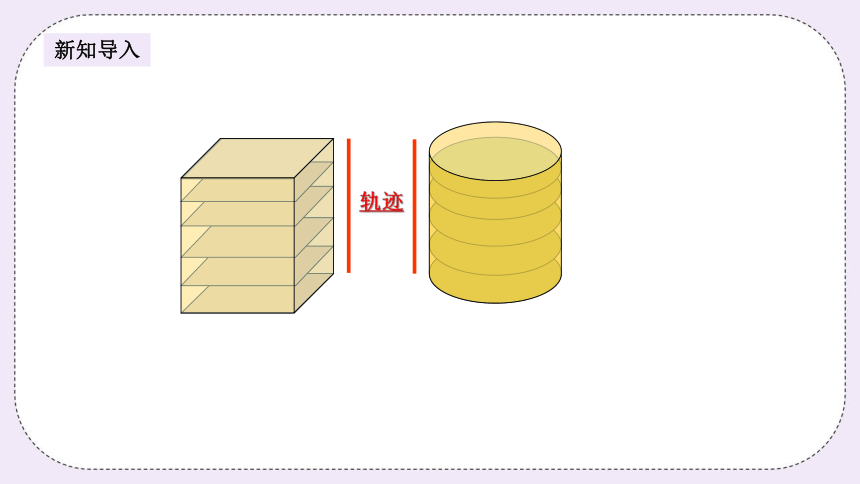
轨迹
新知导入
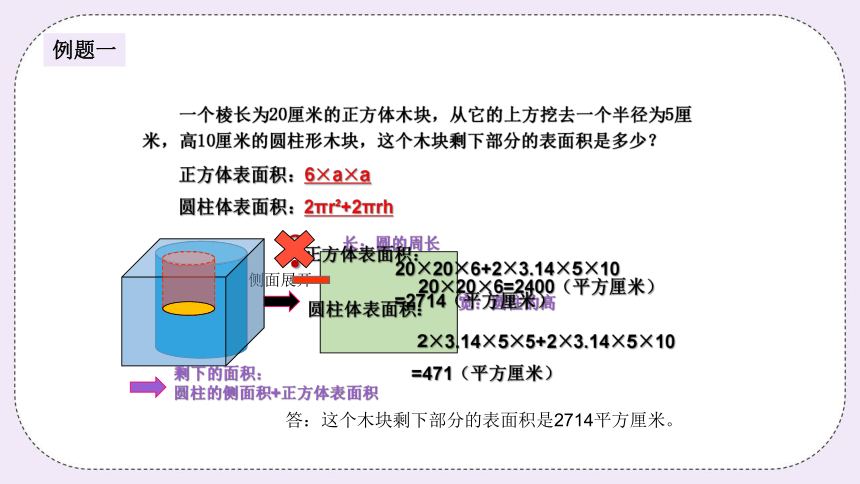
一个棱长为20厘米的正方体木块,从它的上方挖去一个半径为5厘米,高10厘米的圆柱形木块,这个木块剩下部分的表面积是多少?
正方体表面积:6×a×a
圆柱体表面积:2πr +2πrh
侧面展开
长:圆的周长
宽:圆柱的高
正方体表面积:
20×20×6=2400(平方厘米)
圆柱体表面积:
2×3.14×5×5+2×3.14×5×10
=471(平方厘米)
剩下的面积:
圆柱的侧面积+正方体表面积
?
20×20×6+2×3.14×5×10
=2714(平方厘米)
答:这个木块剩下部分的表面积是2714平方厘米。
例题一
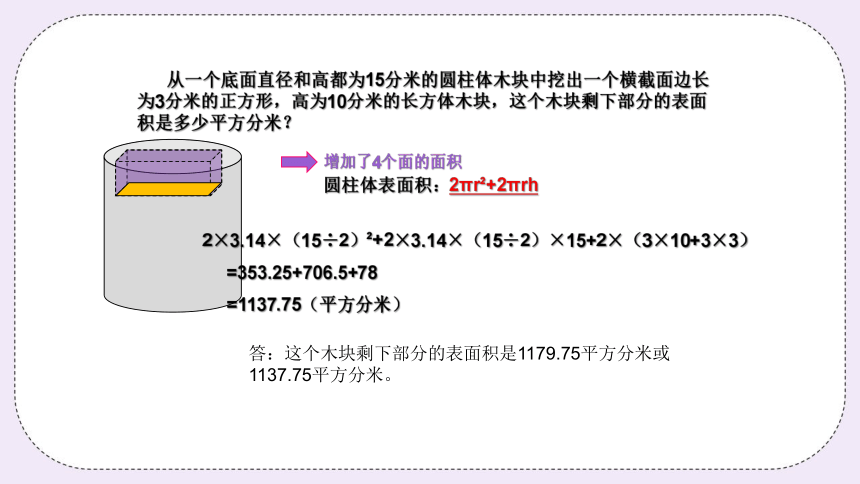
从一个底面直径和高都为15分米的圆柱体木块中挖出一个横截面边长为3分米的正方形,高为10分米的长方体木块,这个木块剩下部分的表面积是多少平方分米?
增加了4个面的面积
2×3.14×(15÷2) +2×3.14×(15÷2)×15+4×3×10
=353.25+706.5+120
=1179.75(平方分米)
圆柱体表面积:2πr +2πrh
同学们,你还能怎么挖?
练习一
从一个底面直径和高都为15分米的圆柱体木块中挖出一个横截面边长为3分米的正方形,高为10分米的长方体木块,这个木块剩下部分的表面积是多少平方分米?
增加了4个面的面积
2×3.14×(15÷2) +2×3.14×(15÷2)×15+2×(3×10+3×3)
=353.25+706.5+78
=1137.75(平方分米)
圆柱体表面积:2πr +2πrh
答:这个木块剩下部分的表面积是1179.75平方分米或1137.75平方分米。
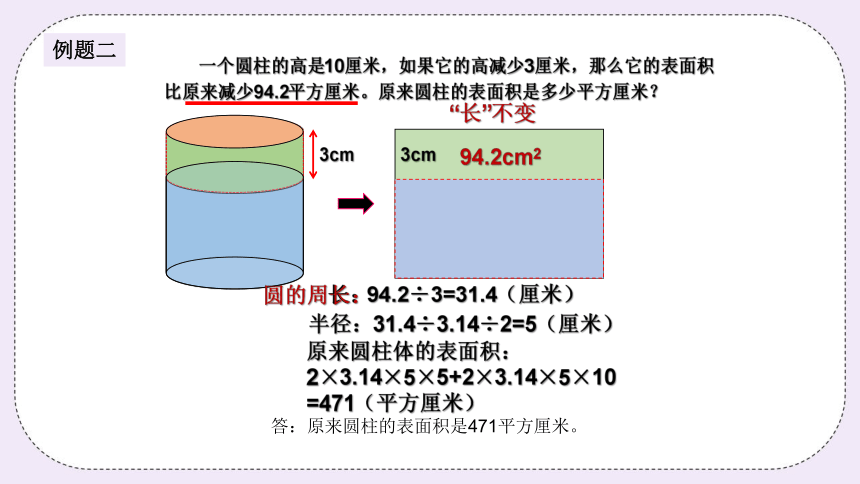
一个圆柱的高是10厘米,如果它的高减少3厘米,那么它的表面积比原来减少94.2平方厘米。原来圆柱的表面积是多少平方厘米?
3cm
3cm
“长”不变
94.2cm2
长:
94.2÷3=31.4(厘米)
圆的周长:
半径:31.4÷3.14÷2=5(厘米)
原来圆柱体的表面积:2×3.14×5×5+2×3.14×5×10=471(平方厘米)
答:原来圆柱的表面积是471平方厘米。
例题二
一段长2米的圆柱体木料切成3段,表面积增加50.24平方厘米。原来这块木料的表面积是多少?
增加了4个圆的面积
半径:50.24÷4÷3.14÷2=2(厘米)
原来木料的表面积:2×3.14×2×2+2×3.14×2×200
=2537.12(平方厘米)
答:原来这块木料的表面积是2537.12平方厘米。
练习二
1. 复习长方体、圆柱体表面积计算公式。
2. 熟悉圆柱体侧面积展开图,熟练地运用公式求解。
小 结
爱迪生是个没有大学文凭的人,他与毕业于美国普林斯顿大学的高材生阿普顿一起工作,他经常受到阿普顿的歧视。有一次,爱迪生拿了个梨形灯泡,请阿普顿测算一下灯泡的容积。于是,阿普顿便拿起灯泡开始测算,只见阿普顿桌子上摆满他画的草图和多张白纸上写着密密麻麻的数据和计算公式,其结果还是没有算出来。阿普顿忙活了好一阵子,急得满头大汗。
爱迪生做完了自己的工作后,走到阿普顿跟前一看,观察和沉思了一会后,笑着说:“阿普顿,你是否可以换用另一种方法计算呢?”接着,爱迪生取来一杯水,给阿普顿刚才反复测算的玻璃灯泡里注满水,然后再把水倒入量筒,几秒钟就测量出水的容积,当然也就是玻璃灯泡的容积了。这时,阿普顿脸羞得通红,呆呆地站在那里,过了一会,不好意思地说:“爱迪生,对不起,过去都是我的不对,以后还得多向您学习。”
把一块棱长为12分米的正方体木料加工成一个体积最大的圆柱,这个圆柱体的体积是多少?加工成体积最大的圆锥体呢?
底面圆的直径等于正方体的棱长
正方体体积公式:棱长×棱长×棱长
长方体体积公式:长×宽×高
圆柱体体积公式:π×半径的平方×高
圆锥体体积公式: ×π×半径的平方×高
圆柱体的体积:
3.14×(12÷2) ×12
=1356.48(立方分米)
①
正方体、长方体、圆柱体体积公式:
底面积×高
圆锥体的体积公式: ×底面积×高
②
× =
等底等高
圆锥体的体积:
×1356.48=452.16(立方分米)
答:最大的圆柱体体积是1356.48分米,圆锥是452.16立方分米。
例题三
把一个底面周长为25.12厘米,高为40厘米的圆柱体铁块重新融化,铸成2个同样大小的高为80厘米的圆锥体铁块,这个圆锥体铁块的底面积有多大?
重铸
体积不变
底面周长25.12厘米
40cm
80cm
半径:25.12÷3.14÷2=4(厘米)
圆柱体体积:
3.14×4×4×40=2009.6(立方厘米)
一个圆锥体体积:
2009.6÷2=1004.8(立方厘米)
圆锥体的体积公式: ×底面积×高
圆锥体的底面积=体积×3÷高
圆锥体的底面积:
1004.8÷80×3=37.68(平方厘米)
答:圆锥体铁块的底面积是37.68平方厘米。
练习三
一个圆柱体木桶,从里面量,底面半径为2分米,里面装有4分米高的水,将一块打磨好的石块完全浸入水中,这时水上升了5厘米。问这个石块的体积是多少立方厘米?
=石头的体积
底面积=3.14×2×2
=12.56(平方分米)
=1256(平方厘米)
体积=1256×5
=6280(立方厘米)
答:这个石块的体积是6280立方厘米。
例题四
一个底面积为36平方分米的长方体水箱,水深20厘米。竖直插入一根长1米,横截面为6平方分米的木料,木料底面与水箱底面接触,水未溢出。水面上涨了多少?
体积=底面积×高
底面积b
水的体积=a×h1
插入木料后的总体积=a×h2
木料的体积=b×h2
水的体积=(a-b)×h2
(a-b)×h2=a×h1
h2=a×h1÷(a-b)
拓展:横截面均匀的立体图形
高=体积÷底面积
水体部分面积:a-b
底面积a
h1
h2
练习四
一个底面积为36平方分米的长方体水箱,水深20厘米。竖直插入一根长1米,横截面为6平方分米的木料,木料底面与水箱底面接触,水未溢出。水面上涨了多少?
h2=a×h1÷(a-b)
水的体积
水后来的底面积
36×20÷10÷(36-6)=2.4(分米)
2.4-20÷10=0.4(分米)
答:水面上涨了0.4分米。
一只高是12厘米的圆柱体玻璃杯中水深6厘米,要在杯中放入一个底和杯的底面积相等,高6厘米圆锥体的铁块,水会不会溢出?如果不会溢出,这时水有多深?
6cm
6cm
等底等高
3×
水不会溢出
物体完全浸没
高=总体积÷底面积
把圆锥的体积作为1份
原来水的体积就是3份,总体积就是4份
底面积不变
高:6÷3×4=8(厘米)
答:这时水深8厘米。
例题五
一个长宽高分别是25分米、24分米、10分米的长方体容器,水面高5分米。放进一个正方体铁块后,铁块顶面仍高于水面。这时水面高6分米。求正方体铁块的体积。
铁块未完全浸没
水未溢出
还记得练习4的公式吗?
h2=a×h1÷(a-b)
a-b=a×h1÷h2
25×24×5÷6=500(平方分米)
正方体铁块底面积:
25×24-500=100(平方分米)
100=10×10
正方体棱长为10分米
10×10×10=1000(立方分米)
答:正方体铁块的体积是1000立方分米。
练习五
1. 掌握小学阶段学习的立体图形的表面积和体积计算。
2. 熟练地运用公式体积=底面积×高,解决生活实际问题。
小 结
课 程 结 束
奥数六年级下册春季课程
第12讲:表面积与体积
奥数六年级下册春季课程
轨迹
新知导入
一个棱长为20厘米的正方体木块,从它的上方挖去一个半径为5厘米,高10厘米的圆柱形木块,这个木块剩下部分的表面积是多少?
正方体表面积:6×a×a
圆柱体表面积:2πr +2πrh
侧面展开
长:圆的周长
宽:圆柱的高
正方体表面积:
20×20×6=2400(平方厘米)
圆柱体表面积:
2×3.14×5×5+2×3.14×5×10
=471(平方厘米)
剩下的面积:
圆柱的侧面积+正方体表面积
?
20×20×6+2×3.14×5×10
=2714(平方厘米)
答:这个木块剩下部分的表面积是2714平方厘米。
例题一
从一个底面直径和高都为15分米的圆柱体木块中挖出一个横截面边长为3分米的正方形,高为10分米的长方体木块,这个木块剩下部分的表面积是多少平方分米?
增加了4个面的面积
2×3.14×(15÷2) +2×3.14×(15÷2)×15+4×3×10
=353.25+706.5+120
=1179.75(平方分米)
圆柱体表面积:2πr +2πrh
同学们,你还能怎么挖?
练习一
从一个底面直径和高都为15分米的圆柱体木块中挖出一个横截面边长为3分米的正方形,高为10分米的长方体木块,这个木块剩下部分的表面积是多少平方分米?
增加了4个面的面积
2×3.14×(15÷2) +2×3.14×(15÷2)×15+2×(3×10+3×3)
=353.25+706.5+78
=1137.75(平方分米)
圆柱体表面积:2πr +2πrh
答:这个木块剩下部分的表面积是1179.75平方分米或1137.75平方分米。
一个圆柱的高是10厘米,如果它的高减少3厘米,那么它的表面积比原来减少94.2平方厘米。原来圆柱的表面积是多少平方厘米?
3cm
3cm
“长”不变
94.2cm2
长:
94.2÷3=31.4(厘米)
圆的周长:
半径:31.4÷3.14÷2=5(厘米)
原来圆柱体的表面积:2×3.14×5×5+2×3.14×5×10=471(平方厘米)
答:原来圆柱的表面积是471平方厘米。
例题二
一段长2米的圆柱体木料切成3段,表面积增加50.24平方厘米。原来这块木料的表面积是多少?
增加了4个圆的面积
半径:50.24÷4÷3.14÷2=2(厘米)
原来木料的表面积:2×3.14×2×2+2×3.14×2×200
=2537.12(平方厘米)
答:原来这块木料的表面积是2537.12平方厘米。
练习二
1. 复习长方体、圆柱体表面积计算公式。
2. 熟悉圆柱体侧面积展开图,熟练地运用公式求解。
小 结
爱迪生是个没有大学文凭的人,他与毕业于美国普林斯顿大学的高材生阿普顿一起工作,他经常受到阿普顿的歧视。有一次,爱迪生拿了个梨形灯泡,请阿普顿测算一下灯泡的容积。于是,阿普顿便拿起灯泡开始测算,只见阿普顿桌子上摆满他画的草图和多张白纸上写着密密麻麻的数据和计算公式,其结果还是没有算出来。阿普顿忙活了好一阵子,急得满头大汗。
爱迪生做完了自己的工作后,走到阿普顿跟前一看,观察和沉思了一会后,笑着说:“阿普顿,你是否可以换用另一种方法计算呢?”接着,爱迪生取来一杯水,给阿普顿刚才反复测算的玻璃灯泡里注满水,然后再把水倒入量筒,几秒钟就测量出水的容积,当然也就是玻璃灯泡的容积了。这时,阿普顿脸羞得通红,呆呆地站在那里,过了一会,不好意思地说:“爱迪生,对不起,过去都是我的不对,以后还得多向您学习。”
把一块棱长为12分米的正方体木料加工成一个体积最大的圆柱,这个圆柱体的体积是多少?加工成体积最大的圆锥体呢?
底面圆的直径等于正方体的棱长
正方体体积公式:棱长×棱长×棱长
长方体体积公式:长×宽×高
圆柱体体积公式:π×半径的平方×高
圆锥体体积公式: ×π×半径的平方×高
圆柱体的体积:
3.14×(12÷2) ×12
=1356.48(立方分米)
①
正方体、长方体、圆柱体体积公式:
底面积×高
圆锥体的体积公式: ×底面积×高
②
× =
等底等高
圆锥体的体积:
×1356.48=452.16(立方分米)
答:最大的圆柱体体积是1356.48分米,圆锥是452.16立方分米。
例题三
把一个底面周长为25.12厘米,高为40厘米的圆柱体铁块重新融化,铸成2个同样大小的高为80厘米的圆锥体铁块,这个圆锥体铁块的底面积有多大?
重铸
体积不变
底面周长25.12厘米
40cm
80cm
半径:25.12÷3.14÷2=4(厘米)
圆柱体体积:
3.14×4×4×40=2009.6(立方厘米)
一个圆锥体体积:
2009.6÷2=1004.8(立方厘米)
圆锥体的体积公式: ×底面积×高
圆锥体的底面积=体积×3÷高
圆锥体的底面积:
1004.8÷80×3=37.68(平方厘米)
答:圆锥体铁块的底面积是37.68平方厘米。
练习三
一个圆柱体木桶,从里面量,底面半径为2分米,里面装有4分米高的水,将一块打磨好的石块完全浸入水中,这时水上升了5厘米。问这个石块的体积是多少立方厘米?
=石头的体积
底面积=3.14×2×2
=12.56(平方分米)
=1256(平方厘米)
体积=1256×5
=6280(立方厘米)
答:这个石块的体积是6280立方厘米。
例题四
一个底面积为36平方分米的长方体水箱,水深20厘米。竖直插入一根长1米,横截面为6平方分米的木料,木料底面与水箱底面接触,水未溢出。水面上涨了多少?
体积=底面积×高
底面积b
水的体积=a×h1
插入木料后的总体积=a×h2
木料的体积=b×h2
水的体积=(a-b)×h2
(a-b)×h2=a×h1
h2=a×h1÷(a-b)
拓展:横截面均匀的立体图形
高=体积÷底面积
水体部分面积:a-b
底面积a
h1
h2
练习四
一个底面积为36平方分米的长方体水箱,水深20厘米。竖直插入一根长1米,横截面为6平方分米的木料,木料底面与水箱底面接触,水未溢出。水面上涨了多少?
h2=a×h1÷(a-b)
水的体积
水后来的底面积
36×20÷10÷(36-6)=2.4(分米)
2.4-20÷10=0.4(分米)
答:水面上涨了0.4分米。
一只高是12厘米的圆柱体玻璃杯中水深6厘米,要在杯中放入一个底和杯的底面积相等,高6厘米圆锥体的铁块,水会不会溢出?如果不会溢出,这时水有多深?
6cm
6cm
等底等高
3×
水不会溢出
物体完全浸没
高=总体积÷底面积
把圆锥的体积作为1份
原来水的体积就是3份,总体积就是4份
底面积不变
高:6÷3×4=8(厘米)
答:这时水深8厘米。
例题五
一个长宽高分别是25分米、24分米、10分米的长方体容器,水面高5分米。放进一个正方体铁块后,铁块顶面仍高于水面。这时水面高6分米。求正方体铁块的体积。
铁块未完全浸没
水未溢出
还记得练习4的公式吗?
h2=a×h1÷(a-b)
a-b=a×h1÷h2
25×24×5÷6=500(平方分米)
正方体铁块底面积:
25×24-500=100(平方分米)
100=10×10
正方体棱长为10分米
10×10×10=1000(立方分米)
答:正方体铁块的体积是1000立方分米。
练习五
1. 掌握小学阶段学习的立体图形的表面积和体积计算。
2. 熟练地运用公式体积=底面积×高,解决生活实际问题。
小 结
课 程 结 束
奥数六年级下册春季课程
