第六章 6.2.1 向量的加法运算 学案(含答案)
文档属性
| 名称 | 第六章 6.2.1 向量的加法运算 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 14:25:10 | ||
图片预览




文档简介
§6.2 平面向量的运算
6.2.1 向量的加法运算
[学习目标]
1.理解并掌握向量加法的概念.
2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.
3.了解向量加法的交换律和结合律,并能作图解释向量加法运算律的合理性.
一、向量加法的三角形法则
问题1 两个向量相加就是两个向量的模相加吗?
问题2 如图,某质点从点A经过点B到点C,这个质点的位移如何表示?
知识梳理
已知非零向量a,b,在平面内取任意一点A,作=a,=b,则向量叫做a与b的和,记作a+b,即a+b=+=.求两个向量和的运算,叫做向量的加法.这种求向量和的方法,称为向量加法的____________法则.
例1 如图所示,
(1)a+b=________;
(2)c+d=________;
(3)a+b+d=________;
(4)c+d+e=________.
反思感悟 向量加法的三角形法则的特征为首尾顺次相接,其和为由第一个向量的起点到最后一个向量的终点,即++…+=.
跟踪训练1 点O是平行四边形ABCD的两条对角线的交点,则++等于( )
A. B. C. D.0
二、向量加法的平行四边形法则
问题3 如图,作AD綉BC,向量与是什么关系?
问题4 由向量加法的三角形法则可知,+=,则+与相等吗?
问题5 四边形ABCD的形状如何?
知识梳理
1.以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量(OC是 OACB的对角线)就是向量a与b的和.把这种作两个向量和的方法叫做向量加法的________________法则.
2.从平行四边形的性质可知三角形法则和平行四边形法则是一致的.
3.对于零向量与任意向量a,规定a+0=0+a=a.
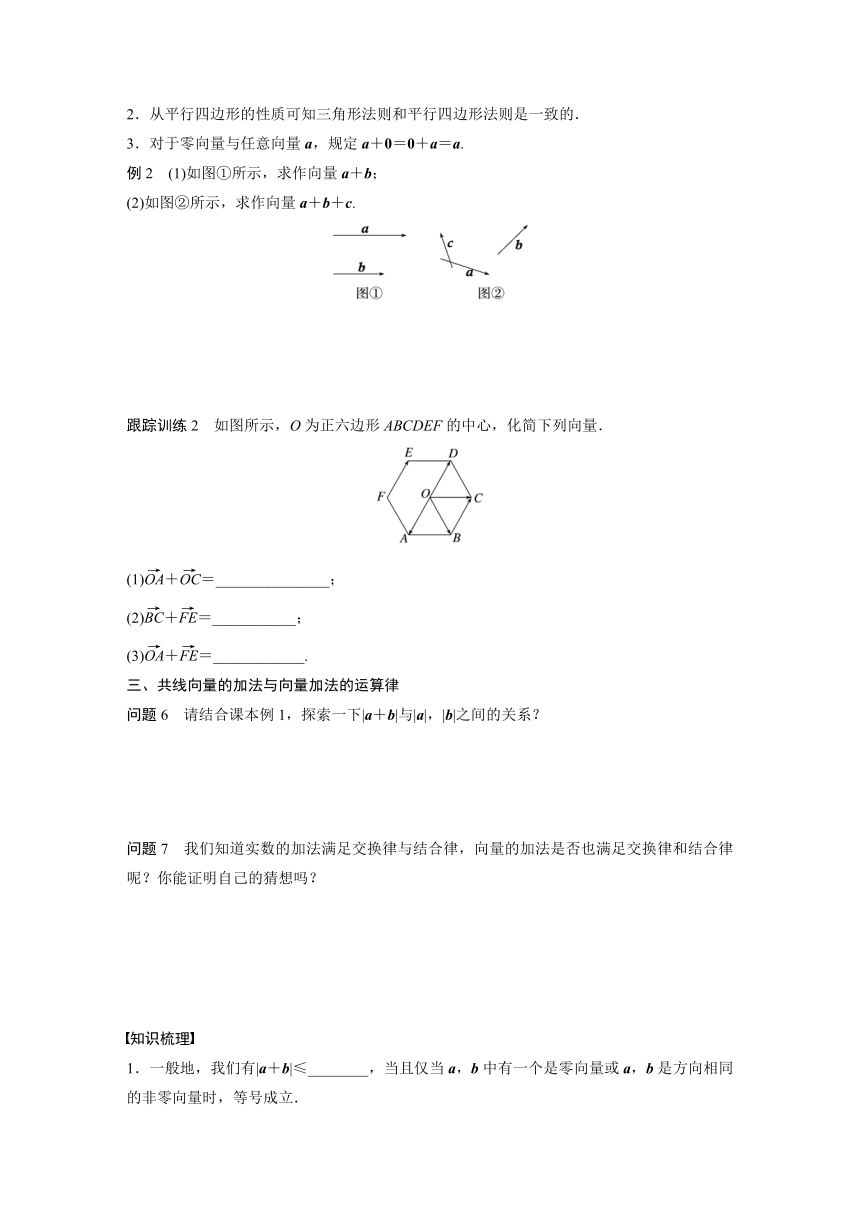
例2 (1)如图①所示,求作向量a+b;
(2)如图②所示,求作向量a+b+c.
跟踪训练2 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
(1)+=_______________;
(2)+=___________;
(3)+=____________.
三、共线向量的加法与向量加法的运算律
问题6 请结合课本例1,探索一下|a+b|与|a|,|b|之间的关系?
问题7 我们知道实数的加法满足交换律与结合律,向量的加法是否也满足交换律和结合律呢?你能证明自己的猜想吗?
知识梳理
1.一般地,我们有|a+b|≤________,当且仅当a,b中有一个是零向量或a,b是方向相同的非零向量时,等号成立.
2.(加法交换律)a+b=________;
(加法结合律)a+(b+c)=________.
例3 (1)已知a,b均为非零向量,且|a+b|=|a|+|b|,则下列说法中正确的是( )
A.a∥b,且a与b的方向相同
B.a,b是方向相反的向量
C.|a|=|b|,且a与b的方向相反
D.a,b无论什么关系均可
(2)化简:
①+;
②++;
③++++.
反思感悟 向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.
(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
跟踪训练3 已知正方形ABCD的边长等于1,则|+++|=________.
四、向量加法的实际应用
例4 河水自西向东流动的速度为10 km/h,小船在静水中的速度为10 km/h,小船自南岸沿正北方向航行,求小船的实际航行速度.
延伸探究 在静水中船的速度的大小为20 m/min,水流的速度的大小为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
反思感悟 应用向量解决实际问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.
跟踪训练4 如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受力的大小.(绳子的重量忽略不计)
1.知识清单:
(1)向量加法的三角形法则.
(2)向量加法的平行四边形法则.
(3)向量三角不等式.
(4)向量加法的运算律.
2.方法归纳:数形结合法.
3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
1.化简++等于( )
A. B. C. D.
2.正方形ABCD的边长为1,则|+|为( )
A.1 B. C.3 D.2
3.(多选)下列等式不正确的是( )
A.a+(b+c)=(a+c)+b
B.+=0
C.=++
D.|a+b|=|a|+|b|
4.如图,四边形ABCD是梯形,AD∥BC,对角线AC与BD相交于点O,则+++等于( )
A. B. C. D.
6.2.1 向量的加法运算
问题1 不是,向量相加要考虑大小及方向,而模相加是数量的加法.
问题2 这个质点两次位移,的结果,与从点A直接到点C的位移的结果相同.因此,位移可以看作位移与合成的,即可以看作与的和.
知识梳理
三角形
例1 (1)c (2)f (3)f (4)g
跟踪训练1 A
问题3 =.
问题4 相等.
问题5 平行四边形.
知识梳理
1.平行四边形
例2 解 (1)首先作向量=a,然后作向量=b,则向量=a+b.如图③所示.
(2)方法一 (三角形法则)如图④所示,
首先在平面内任取一点O,作向量=a,再作向量=b,则得向量=a+b,然后作向量=c,则向量=a+b+c即为所求.
方法二 (平行四边形法则)如图⑤所示,
首先在平面内任取一点O,作向量=a,=b,=c,
以OA,OB为邻边作 OADB,连接OD,
则=+=a+b.
再以OD,OC为邻边作 ODEC,连接OE,
则=+=a+b+c即为所求.
跟踪训练2 (1) (2) (3)0
解析 (1)因为四边形OABC是以OA,OC为邻边的平行四边形,OB是其对角线,故+=.
(2)因为=,
故+与方向相同,
长度为的长度的2倍,
故+=.
(3)因为=,
故+=+=0.
问题6 (1)当向量a与b不共线时,a+b的方向与a,b方向不同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b同向,且|a+b|=|a|+|b|.
(3)当a与b反向时,若|a|>|b|,则a+b的方向与a相同,且|a+b|=|a|-|b|;若|a|<|b|,则a+b的方向与b相同,且|a+b|=|b|-|a|.
问题7 如图1,作=a,=b,以AB,AD为邻边作 ABCD,容易发现=b,=a,故=+=a+b.又=+=b+a,所以a+b=b+a.所以满足交换律.
如图2,不难证明满足结合律.
知识梳理
1.|a|+|b|
2.b+a (a+b)+c
例3 (1)A [因为|a+b|≤|a|+|b|(当且仅当a与b方向相同时取等号).]
(2)解 ①+=+=.
②++=++
=(+)+=+=0.
③++++
=++++
=+++
=++
=+=0.
跟踪训练3 2
解析 |+++|
=|+++|
=|+|=2||=2.
例4 解 设a,b分别表示水流的速度和小船在静水中的速度,过平面内任意一点O作=a,=b,以OA,OB为邻边作矩形OACB,连接OC,如图,则=a+b,并且即为小船的实际航行速度.
∴||==20(km/h),
∵tan∠AOC==,
∴∠AOC=60°,
∴小船的实际航行速度的大小为20 km/h,沿北偏东30°的方向航行.
延伸探究 解 作出图形,如图所示.船速v船与岸的方向成角α,由图可知v水+v船=v实际,结合已知条件,
四边形ABCD为平行四边形,
在Rt△ACD中,
||=||=|v水|=10,
||=|v船|=20,
所以cos α===,
所以α=60°,
从而船与水流方向成120°的角.
所以船是沿与水流的方向成120°角的方向行进.
跟踪训练4 解 如图所示,设,分别表示A,B所受的力,10 N的重力用表示,
则+=.
由题意可得
∠ECG=180°-150°=30°,
∠FCG=180°-120°=60°.
∴||=||cos 30°
=10×=5(N),
||=||cos 60°
=10×=5(N).
∴A处所受力的大小为5 N,B处所受力的大小为5 N.
随堂演练
1.C 2.B 3.BD 4.B
6.2.1 向量的加法运算
[学习目标]
1.理解并掌握向量加法的概念.
2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.
3.了解向量加法的交换律和结合律,并能作图解释向量加法运算律的合理性.
一、向量加法的三角形法则
问题1 两个向量相加就是两个向量的模相加吗?
问题2 如图,某质点从点A经过点B到点C,这个质点的位移如何表示?
知识梳理
已知非零向量a,b,在平面内取任意一点A,作=a,=b,则向量叫做a与b的和,记作a+b,即a+b=+=.求两个向量和的运算,叫做向量的加法.这种求向量和的方法,称为向量加法的____________法则.
例1 如图所示,
(1)a+b=________;
(2)c+d=________;
(3)a+b+d=________;
(4)c+d+e=________.
反思感悟 向量加法的三角形法则的特征为首尾顺次相接,其和为由第一个向量的起点到最后一个向量的终点,即++…+=.
跟踪训练1 点O是平行四边形ABCD的两条对角线的交点,则++等于( )
A. B. C. D.0
二、向量加法的平行四边形法则
问题3 如图,作AD綉BC,向量与是什么关系?
问题4 由向量加法的三角形法则可知,+=,则+与相等吗?
问题5 四边形ABCD的形状如何?
知识梳理
1.以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量(OC是 OACB的对角线)就是向量a与b的和.把这种作两个向量和的方法叫做向量加法的________________法则.
2.从平行四边形的性质可知三角形法则和平行四边形法则是一致的.
3.对于零向量与任意向量a,规定a+0=0+a=a.
例2 (1)如图①所示,求作向量a+b;
(2)如图②所示,求作向量a+b+c.
跟踪训练2 如图所示,O为正六边形ABCDEF的中心,化简下列向量.
(1)+=_______________;
(2)+=___________;
(3)+=____________.
三、共线向量的加法与向量加法的运算律
问题6 请结合课本例1,探索一下|a+b|与|a|,|b|之间的关系?
问题7 我们知道实数的加法满足交换律与结合律,向量的加法是否也满足交换律和结合律呢?你能证明自己的猜想吗?
知识梳理
1.一般地,我们有|a+b|≤________,当且仅当a,b中有一个是零向量或a,b是方向相同的非零向量时,等号成立.
2.(加法交换律)a+b=________;
(加法结合律)a+(b+c)=________.
例3 (1)已知a,b均为非零向量,且|a+b|=|a|+|b|,则下列说法中正确的是( )
A.a∥b,且a与b的方向相同
B.a,b是方向相反的向量
C.|a|=|b|,且a与b的方向相反
D.a,b无论什么关系均可
(2)化简:
①+;
②++;
③++++.
反思感悟 向量加法运算律的意义和应用原则
(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现了恰当利用向量加法法则运算的目的.
(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.
跟踪训练3 已知正方形ABCD的边长等于1,则|+++|=________.
四、向量加法的实际应用
例4 河水自西向东流动的速度为10 km/h,小船在静水中的速度为10 km/h,小船自南岸沿正北方向航行,求小船的实际航行速度.
延伸探究 在静水中船的速度的大小为20 m/min,水流的速度的大小为10 m/min,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向.
反思感悟 应用向量解决实际问题的基本步骤
(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.
(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.
(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.
跟踪训练4 如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受力的大小.(绳子的重量忽略不计)
1.知识清单:
(1)向量加法的三角形法则.
(2)向量加法的平行四边形法则.
(3)向量三角不等式.
(4)向量加法的运算律.
2.方法归纳:数形结合法.
3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.
1.化简++等于( )
A. B. C. D.
2.正方形ABCD的边长为1,则|+|为( )
A.1 B. C.3 D.2
3.(多选)下列等式不正确的是( )
A.a+(b+c)=(a+c)+b
B.+=0
C.=++
D.|a+b|=|a|+|b|
4.如图,四边形ABCD是梯形,AD∥BC,对角线AC与BD相交于点O,则+++等于( )
A. B. C. D.
6.2.1 向量的加法运算
问题1 不是,向量相加要考虑大小及方向,而模相加是数量的加法.
问题2 这个质点两次位移,的结果,与从点A直接到点C的位移的结果相同.因此,位移可以看作位移与合成的,即可以看作与的和.
知识梳理
三角形
例1 (1)c (2)f (3)f (4)g
跟踪训练1 A
问题3 =.
问题4 相等.
问题5 平行四边形.
知识梳理
1.平行四边形
例2 解 (1)首先作向量=a,然后作向量=b,则向量=a+b.如图③所示.
(2)方法一 (三角形法则)如图④所示,
首先在平面内任取一点O,作向量=a,再作向量=b,则得向量=a+b,然后作向量=c,则向量=a+b+c即为所求.
方法二 (平行四边形法则)如图⑤所示,
首先在平面内任取一点O,作向量=a,=b,=c,
以OA,OB为邻边作 OADB,连接OD,
则=+=a+b.
再以OD,OC为邻边作 ODEC,连接OE,
则=+=a+b+c即为所求.
跟踪训练2 (1) (2) (3)0
解析 (1)因为四边形OABC是以OA,OC为邻边的平行四边形,OB是其对角线,故+=.
(2)因为=,
故+与方向相同,
长度为的长度的2倍,
故+=.
(3)因为=,
故+=+=0.
问题6 (1)当向量a与b不共线时,a+b的方向与a,b方向不同,且|a+b|<|a|+|b|.
(2)当a与b同向时,a+b,a,b同向,且|a+b|=|a|+|b|.
(3)当a与b反向时,若|a|>|b|,则a+b的方向与a相同,且|a+b|=|a|-|b|;若|a|<|b|,则a+b的方向与b相同,且|a+b|=|b|-|a|.
问题7 如图1,作=a,=b,以AB,AD为邻边作 ABCD,容易发现=b,=a,故=+=a+b.又=+=b+a,所以a+b=b+a.所以满足交换律.
如图2,不难证明满足结合律.
知识梳理
1.|a|+|b|
2.b+a (a+b)+c
例3 (1)A [因为|a+b|≤|a|+|b|(当且仅当a与b方向相同时取等号).]
(2)解 ①+=+=.
②++=++
=(+)+=+=0.
③++++
=++++
=+++
=++
=+=0.
跟踪训练3 2
解析 |+++|
=|+++|
=|+|=2||=2.
例4 解 设a,b分别表示水流的速度和小船在静水中的速度,过平面内任意一点O作=a,=b,以OA,OB为邻边作矩形OACB,连接OC,如图,则=a+b,并且即为小船的实际航行速度.
∴||==20(km/h),
∵tan∠AOC==,
∴∠AOC=60°,
∴小船的实际航行速度的大小为20 km/h,沿北偏东30°的方向航行.
延伸探究 解 作出图形,如图所示.船速v船与岸的方向成角α,由图可知v水+v船=v实际,结合已知条件,
四边形ABCD为平行四边形,
在Rt△ACD中,
||=||=|v水|=10,
||=|v船|=20,
所以cos α===,
所以α=60°,
从而船与水流方向成120°的角.
所以船是沿与水流的方向成120°角的方向行进.
跟踪训练4 解 如图所示,设,分别表示A,B所受的力,10 N的重力用表示,
则+=.
由题意可得
∠ECG=180°-150°=30°,
∠FCG=180°-120°=60°.
∴||=||cos 30°
=10×=5(N),
||=||cos 60°
=10×=5(N).
∴A处所受力的大小为5 N,B处所受力的大小为5 N.
随堂演练
1.C 2.B 3.BD 4.B
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
