六年级下册数学人教版奥数专讲:工工程问题(课件)(共25张PPT)
文档属性
| 名称 | 六年级下册数学人教版奥数专讲:工工程问题(课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 13:43:11 | ||
图片预览







文档简介
(共25张PPT)
第4讲:工程问题
奥数六年级下册春季课程
你知道中国古代三大工程吗?
新知导入
长城,又称万里长城,是中国古代的军事防御工程。春秋战国时期列国争霸,互相防守,长城修筑进入第一个高潮,但此时修筑的长度都比较短。秦灭六国统一天下后,秦始皇连接和修缮战国长城,始有万里长城之称 。明朝是最后一个大修长城的朝代,今天人们所看到的长城多是此时修筑。明长城总长度为8851.8千米,秦汉及早期长城超过1万千米,总长超过2.1万千米。1987年12月,长城被列入世界文化遗产。
京杭大运河是世界上里程最长、工程最大的古代运河,并且使用至今,是中国古代劳动人民创造的一项伟大工程,是中国文化地位的象征之一。大运河南起余杭(今杭州),北到涿郡(今北京),全长约1797公里。运河对中国南北地区之间的经济、文化发展与交流,特别是对沿线地区工农业经济的发展起了巨大作用。
坎儿井,是荒漠地区一特殊灌溉系统,普遍于中国新疆吐鲁番地区。吐鲁番的坎儿井总数达1100多条,全长约5000公里。坎儿井是开发利用地下水的一种很古老式的水平集水建筑物,适用于山麓、冲积扇缘地带,主要是用于截取地下潜水来进行农田灌溉和居民用水。人们利用山的坡度,巧妙地创造了坎儿井,引地下潜流灌溉农田。坎儿井不因炎热、狂风而使水分大量蒸发,因而流量稳定,保证了自流灌溉。
修完一段路需要5天,每天修这段路的多少?
每天修一段路的 ,修完这段路需要多少天?
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
单位“1”
一份工作,卡尔5小时先完成了 ,欧拉6小时又完成了剩下任务的一半,最后余下的部分由卡尔、欧拉合作,还需要多少时间才能完成?
卡尔的工作效率:
欧拉的工作效率:
剩余所需工作时间:
÷5
=
答:还需要 小时。
=
单位“1”
剩余工作量的一半:
(1- )×
=
÷6
卡尔、欧拉合作的工作效率:
+
=
÷
= (小时)
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
例题一
单位“1”
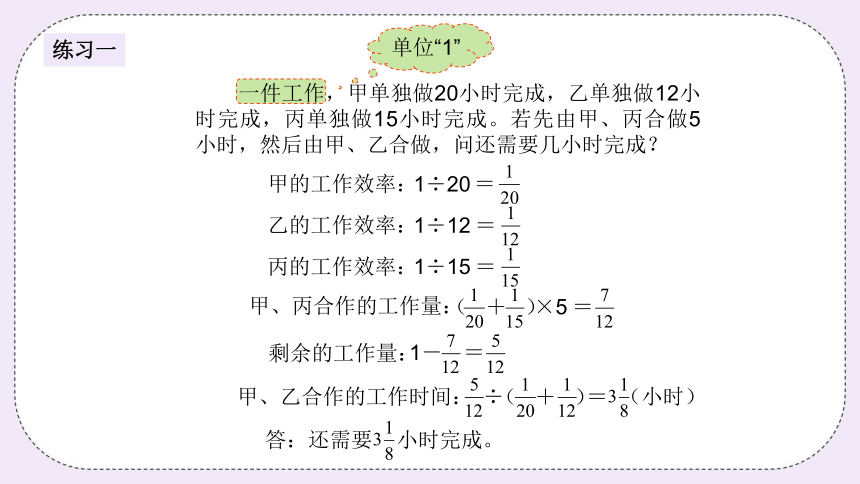
一件工作,甲单独做20小时完成,乙单独做12小时完成,丙单独做15小时完成。若先由甲、丙合做5小时,然后由甲、乙合做,问还需要几小时完成?
甲的工作效率:
1÷20
=
乙的工作效率:
1÷12
=
丙的工作效率:
1÷15
=
甲、丙合作的工作量:
×5
( + )
= (小时)
剩余的工作量:
1-
=
甲、乙合作的工作时间:
÷
( + )
=
答:还需要 小时完成。
练习一
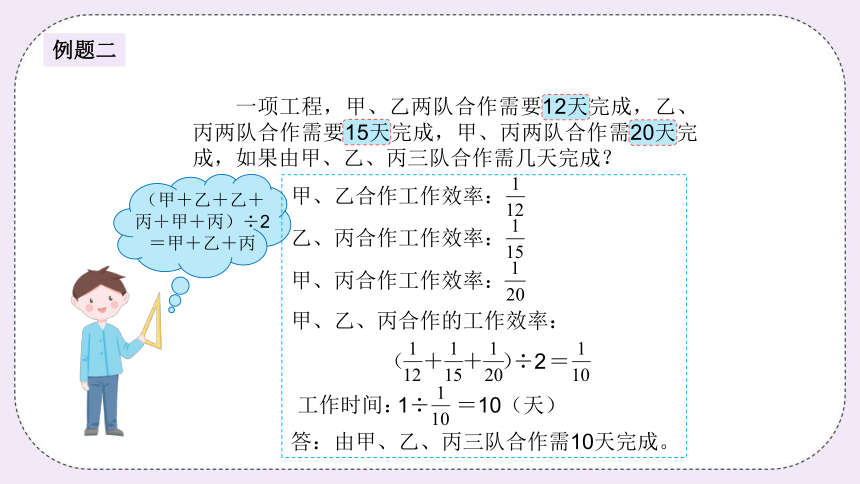
一项工程,甲、乙两队合作需要12天完成,乙、丙两队合作需要15天完成,甲、丙两队合作需20天完成,如果由甲、乙、丙三队合作需几天完成?
答:由甲、乙、丙三队合作需10天完成。
=10(天)
÷2
甲、乙合作工作效率:
乙、丙合作工作效率:
甲、丙合作工作效率:
(甲+乙+乙+
丙+甲+丙)÷2
=甲+乙+丙
甲、乙、丙合作的工作效率:
( + + )
=
1÷
工作时间:
例题二
如果用甲、乙、丙三根水管同时在一个空水池里灌水,1小时可以灌满;如果用甲、乙两管,1小时20分钟可以灌满;如果用乙、丙两根水管,1小时15分钟可以灌满。那么,用乙管单独灌水的话,灌满这一池需要多少小时?
1小时15分钟=
1小时20分钟=
小时
小时
甲、乙、丙的工作效率:
1
甲、乙的工作效率:
乙、丙的工作效率:
1÷
1÷
=
=
乙独灌工作效率:
+ -1
=
乙独灌工作时间:
= (小时)
1÷
答:灌满这一池需要 小时。
(甲+乙+乙+丙)
-(甲+乙+丙)
=乙
练习二
1. 在解决工程问题时,一般把工作总量看作
,然后表示各个工作效率。
(工作时间=1÷工作效率)
(工作效率=1÷工作时间)
(1=工作时间×工作效率)
单位“1”
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
2.
小 结
你知道中国新世纪四大工程吗?
“南水北调工程”是中华人民共和国的战略性工程。是指把长江流域水资源自其上游、中游、下游,结合中国疆土地域特点,分东、中、西三线抽调部分送至华北与淮海平原和西北地区水资源短缺地区。
青藏铁路起于青海省西宁市,途经格尔木市、昆仑山口、沱沱河沿,翻越唐古拉山口,进入西藏自治区安多、那曲、当雄、羊八井、拉萨。全长1956千米,是重要的进藏路线,被誉为天路,是世界上海拔最高、在冻土上路程最长的高原铁路,2013年9月入选“全球百年工程”,是世界铁路建设史上的一座丰碑。
“西气东输”,我国距离最长、口径最大的输气道管,西起塔里木盆地的轮南,东至上海。全线采用自动化控制,供气范围覆盖中原、华东、长江三角洲地区。自新疆轮台县塔里木轮南油气田,向东经过吐鲁番、酒泉、兰州、西安、洛阳、合肥、南京等地区。东西横贯新疆、陕西、山西、安徽、浙江、上海等10个省区,全长4200千米。
我国煤炭资源主要分布在西部和北部地区,水能资源主要集中在西南地区,东部地区的一次能源资源匮乏、用电负荷相对集中。能源资源与电力负荷分布的不均衡性决定了西电东送的必要性。"西电东送"就是把煤炭、水能资源丰富的西部省区的能源转化成电力资源,输送到电力紧缺的东部沿海地区。
一件工作,甲、乙合作需4小时完成,乙、丙合作需5小时完成。现在先请甲、丙合作2小时后,余下的乙还需做6小时完成。乙单独做完这件工作需要多少小时?
甲、乙合作2小时,
乙、丙合作2小时,
乙独做2小时。
甲、乙合作的工作效率:
乙、丙合作的工作效率:
乙的工作效率:
=
=20(小时)
乙独做的工作时间:
1÷
(1- ×2- ×2)
÷2
答:乙单独做完这件工作需要20小时。
例题三
阿博士需要小伙伴们帮忙清理一片草地。若米德和欧拉合作需要3小时完成,若卡尔和欧拉合作需要6小时完成。现在,米德和卡尔合作了1小时后,欧拉才来,于是欧拉单独花了6小时清理完了剩下的草地。如果由欧拉单独做这件事,欧拉需要多少小时?
米、欧合作1小时,
卡、欧合作1小时,
欧拉独做4小时。
米、欧合作的工作效率:
卡、欧合作的工作效率:
欧拉的工作效率:
=
=8(小时)
欧拉独做的工作时间:
1÷
(1- ×1- ×1)
÷4
答:欧拉单独做需要8小时。
练习三
有一件工作,米德独做要20天完成,阿博士独做要12天完成。这件工作先由米德做了若干天,然后由阿博士继续做完,从开始到完工共用了14天。这件工作由米德先做了几天?
米德也做了几天!
假设这14天都由阿博士做
工作总量为:
×14
=
比实际多做了:
-1
=
阿博士每天比米德多做:
-
=
米德做的天数:
÷
=5(天)
答:这件工作由米德先做了5天。
例题四
一项工程,甲独做12天完成,乙独做4天完成。若甲先做若干天后,由乙接着做余下的工程,直至完成全部任务,这样前后共用了6天,甲先做了几天?
甲也做了几天!
假设这6天都由乙做
工作总量为:
×6
=
比实际多做了:
-1
=
乙每天比甲多做:
-
=
甲做的天数:
÷
=3(天)
答:甲先做了3天。
练习四
一件工作甲先做6小时,乙接着做12小时可完成。甲先做8小时,乙接着做6小时也可以完成。如果甲做3小时后由乙接着做,还需要多少小时完成?
(1- ×3)
方法一:
甲做2小时的工作量=
+
甲做6小时
乙做12小时
+
甲做8小时
乙做6小时
这件工作甲单独做要
这件工作乙单独做要
=21(小时)
÷
10小时
30小时
乙做6小时的工作量
答:还需要21小时完成。
例题五
一件工作甲先做6小时,乙接着做12小时可完成。甲先做8小时,乙接着做6小时也可以完成。如果甲做3小时后由乙接着做,还需要多少小时完成?
方法二:
甲做2小时的工作量=
+
甲做6小时
乙做12小时
+
甲做8小时
乙做6小时
这件工作乙单独做要30小时
乙做6小时的工作量
甲独做3小时相当于乙做了:
30-9=21(小时)
3×
=9(小时)
乙还需要做:
答:还需要21小时完成。
一项工程,甲做10天乙做20天完成,或甲做15天乙做12天也能完成。现在乙先做4天,问甲还要做多少天完成?
方法二:
甲做5天的工作量=
甲做15天+乙做12天
甲做10天+乙做20天
乙做8天的工作量
乙独做4天相当于甲做了:
22.5-2.5=20(天)
4×
=2.5(天)
甲还需要做:
答:甲还要做20天完成。
甲独做需要:
15+
=22.5(天)
12×
练习五
1. 在解决工程问题时,一般把工作总量看作
,然后表示各个工作效率。
(工作时间=1÷工作效率)
(工作效率=1÷工作时间)
(1=工作时间×工作效率)
单位“1”
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
2.
3. 在工程问题中,遇到合作和分工时,需要
灵活转换条件,使之可以利用已知条件解
题。
小 结
课 程 结 束
奥数六年级下册春季课程
第4讲:工程问题
奥数六年级下册春季课程
你知道中国古代三大工程吗?
新知导入
长城,又称万里长城,是中国古代的军事防御工程。春秋战国时期列国争霸,互相防守,长城修筑进入第一个高潮,但此时修筑的长度都比较短。秦灭六国统一天下后,秦始皇连接和修缮战国长城,始有万里长城之称 。明朝是最后一个大修长城的朝代,今天人们所看到的长城多是此时修筑。明长城总长度为8851.8千米,秦汉及早期长城超过1万千米,总长超过2.1万千米。1987年12月,长城被列入世界文化遗产。
京杭大运河是世界上里程最长、工程最大的古代运河,并且使用至今,是中国古代劳动人民创造的一项伟大工程,是中国文化地位的象征之一。大运河南起余杭(今杭州),北到涿郡(今北京),全长约1797公里。运河对中国南北地区之间的经济、文化发展与交流,特别是对沿线地区工农业经济的发展起了巨大作用。
坎儿井,是荒漠地区一特殊灌溉系统,普遍于中国新疆吐鲁番地区。吐鲁番的坎儿井总数达1100多条,全长约5000公里。坎儿井是开发利用地下水的一种很古老式的水平集水建筑物,适用于山麓、冲积扇缘地带,主要是用于截取地下潜水来进行农田灌溉和居民用水。人们利用山的坡度,巧妙地创造了坎儿井,引地下潜流灌溉农田。坎儿井不因炎热、狂风而使水分大量蒸发,因而流量稳定,保证了自流灌溉。
修完一段路需要5天,每天修这段路的多少?
每天修一段路的 ,修完这段路需要多少天?
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
单位“1”
一份工作,卡尔5小时先完成了 ,欧拉6小时又完成了剩下任务的一半,最后余下的部分由卡尔、欧拉合作,还需要多少时间才能完成?
卡尔的工作效率:
欧拉的工作效率:
剩余所需工作时间:
÷5
=
答:还需要 小时。
=
单位“1”
剩余工作量的一半:
(1- )×
=
÷6
卡尔、欧拉合作的工作效率:
+
=
÷
= (小时)
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
例题一
单位“1”
一件工作,甲单独做20小时完成,乙单独做12小时完成,丙单独做15小时完成。若先由甲、丙合做5小时,然后由甲、乙合做,问还需要几小时完成?
甲的工作效率:
1÷20
=
乙的工作效率:
1÷12
=
丙的工作效率:
1÷15
=
甲、丙合作的工作量:
×5
( + )
= (小时)
剩余的工作量:
1-
=
甲、乙合作的工作时间:
÷
( + )
=
答:还需要 小时完成。
练习一
一项工程,甲、乙两队合作需要12天完成,乙、丙两队合作需要15天完成,甲、丙两队合作需20天完成,如果由甲、乙、丙三队合作需几天完成?
答:由甲、乙、丙三队合作需10天完成。
=10(天)
÷2
甲、乙合作工作效率:
乙、丙合作工作效率:
甲、丙合作工作效率:
(甲+乙+乙+
丙+甲+丙)÷2
=甲+乙+丙
甲、乙、丙合作的工作效率:
( + + )
=
1÷
工作时间:
例题二
如果用甲、乙、丙三根水管同时在一个空水池里灌水,1小时可以灌满;如果用甲、乙两管,1小时20分钟可以灌满;如果用乙、丙两根水管,1小时15分钟可以灌满。那么,用乙管单独灌水的话,灌满这一池需要多少小时?
1小时15分钟=
1小时20分钟=
小时
小时
甲、乙、丙的工作效率:
1
甲、乙的工作效率:
乙、丙的工作效率:
1÷
1÷
=
=
乙独灌工作效率:
+ -1
=
乙独灌工作时间:
= (小时)
1÷
答:灌满这一池需要 小时。
(甲+乙+乙+丙)
-(甲+乙+丙)
=乙
练习二
1. 在解决工程问题时,一般把工作总量看作
,然后表示各个工作效率。
(工作时间=1÷工作效率)
(工作效率=1÷工作时间)
(1=工作时间×工作效率)
单位“1”
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
2.
小 结
你知道中国新世纪四大工程吗?
“南水北调工程”是中华人民共和国的战略性工程。是指把长江流域水资源自其上游、中游、下游,结合中国疆土地域特点,分东、中、西三线抽调部分送至华北与淮海平原和西北地区水资源短缺地区。
青藏铁路起于青海省西宁市,途经格尔木市、昆仑山口、沱沱河沿,翻越唐古拉山口,进入西藏自治区安多、那曲、当雄、羊八井、拉萨。全长1956千米,是重要的进藏路线,被誉为天路,是世界上海拔最高、在冻土上路程最长的高原铁路,2013年9月入选“全球百年工程”,是世界铁路建设史上的一座丰碑。
“西气东输”,我国距离最长、口径最大的输气道管,西起塔里木盆地的轮南,东至上海。全线采用自动化控制,供气范围覆盖中原、华东、长江三角洲地区。自新疆轮台县塔里木轮南油气田,向东经过吐鲁番、酒泉、兰州、西安、洛阳、合肥、南京等地区。东西横贯新疆、陕西、山西、安徽、浙江、上海等10个省区,全长4200千米。
我国煤炭资源主要分布在西部和北部地区,水能资源主要集中在西南地区,东部地区的一次能源资源匮乏、用电负荷相对集中。能源资源与电力负荷分布的不均衡性决定了西电东送的必要性。"西电东送"就是把煤炭、水能资源丰富的西部省区的能源转化成电力资源,输送到电力紧缺的东部沿海地区。
一件工作,甲、乙合作需4小时完成,乙、丙合作需5小时完成。现在先请甲、丙合作2小时后,余下的乙还需做6小时完成。乙单独做完这件工作需要多少小时?
甲、乙合作2小时,
乙、丙合作2小时,
乙独做2小时。
甲、乙合作的工作效率:
乙、丙合作的工作效率:
乙的工作效率:
=
=20(小时)
乙独做的工作时间:
1÷
(1- ×2- ×2)
÷2
答:乙单独做完这件工作需要20小时。
例题三
阿博士需要小伙伴们帮忙清理一片草地。若米德和欧拉合作需要3小时完成,若卡尔和欧拉合作需要6小时完成。现在,米德和卡尔合作了1小时后,欧拉才来,于是欧拉单独花了6小时清理完了剩下的草地。如果由欧拉单独做这件事,欧拉需要多少小时?
米、欧合作1小时,
卡、欧合作1小时,
欧拉独做4小时。
米、欧合作的工作效率:
卡、欧合作的工作效率:
欧拉的工作效率:
=
=8(小时)
欧拉独做的工作时间:
1÷
(1- ×1- ×1)
÷4
答:欧拉单独做需要8小时。
练习三
有一件工作,米德独做要20天完成,阿博士独做要12天完成。这件工作先由米德做了若干天,然后由阿博士继续做完,从开始到完工共用了14天。这件工作由米德先做了几天?
米德也做了几天!
假设这14天都由阿博士做
工作总量为:
×14
=
比实际多做了:
-1
=
阿博士每天比米德多做:
-
=
米德做的天数:
÷
=5(天)
答:这件工作由米德先做了5天。
例题四
一项工程,甲独做12天完成,乙独做4天完成。若甲先做若干天后,由乙接着做余下的工程,直至完成全部任务,这样前后共用了6天,甲先做了几天?
甲也做了几天!
假设这6天都由乙做
工作总量为:
×6
=
比实际多做了:
-1
=
乙每天比甲多做:
-
=
甲做的天数:
÷
=3(天)
答:甲先做了3天。
练习四
一件工作甲先做6小时,乙接着做12小时可完成。甲先做8小时,乙接着做6小时也可以完成。如果甲做3小时后由乙接着做,还需要多少小时完成?
(1- ×3)
方法一:
甲做2小时的工作量=
+
甲做6小时
乙做12小时
+
甲做8小时
乙做6小时
这件工作甲单独做要
这件工作乙单独做要
=21(小时)
÷
10小时
30小时
乙做6小时的工作量
答:还需要21小时完成。
例题五
一件工作甲先做6小时,乙接着做12小时可完成。甲先做8小时,乙接着做6小时也可以完成。如果甲做3小时后由乙接着做,还需要多少小时完成?
方法二:
甲做2小时的工作量=
+
甲做6小时
乙做12小时
+
甲做8小时
乙做6小时
这件工作乙单独做要30小时
乙做6小时的工作量
甲独做3小时相当于乙做了:
30-9=21(小时)
3×
=9(小时)
乙还需要做:
答:还需要21小时完成。
一项工程,甲做10天乙做20天完成,或甲做15天乙做12天也能完成。现在乙先做4天,问甲还要做多少天完成?
方法二:
甲做5天的工作量=
甲做15天+乙做12天
甲做10天+乙做20天
乙做8天的工作量
乙独做4天相当于甲做了:
22.5-2.5=20(天)
4×
=2.5(天)
甲还需要做:
答:甲还要做20天完成。
甲独做需要:
15+
=22.5(天)
12×
练习五
1. 在解决工程问题时,一般把工作总量看作
,然后表示各个工作效率。
(工作时间=1÷工作效率)
(工作效率=1÷工作时间)
(1=工作时间×工作效率)
单位“1”
工作效率=
工作总量÷工作时间
工作总量÷工作效率
工作时间×工作效率
工作时间=
工作总量=
2.
3. 在工程问题中,遇到合作和分工时,需要
灵活转换条件,使之可以利用已知条件解
题。
小 结
课 程 结 束
奥数六年级下册春季课程
