湖北省武汉市华中师范大学第一附属中学2023-2024学年高二上学期期末模拟数学试题(无答案)
文档属性
| 名称 | 湖北省武汉市华中师范大学第一附属中学2023-2024学年高二上学期期末模拟数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-14 20:30:51 | ||
图片预览

文档简介
华中师大一附中2022级高二上学期期末模拟试题
一、单项选择题:本题共8小题,每小题5分,共40分.
1.已知不共线的三个空间向量,,,,则一定共线的三个点是
A.、、 B.、、 C.、、 D.、、
2.设直线与关于直线对称,则直线的方程是
A. B. C. D.
3.已知为等比数列,为数列的前项和,,则的值为
A.3 B.18 C.54 D.152
4.已知圆的方程为,点在直线上,线段为圆的直径,则的最小值为
A.2 B. C.3 D.
5.已知点是双曲线上的动点,为该双曲线的左右焦点,为坐标原点,则的最大值为
A. B.2 C. D.
6.若数列的通项公式是,则的值为
A. B. C. D.
7.如图所示,是双曲线的左右焦点,的右支上存在一点满足,与的左支的交点满足,则双曲线的离心率为
A.3 B. C. D.
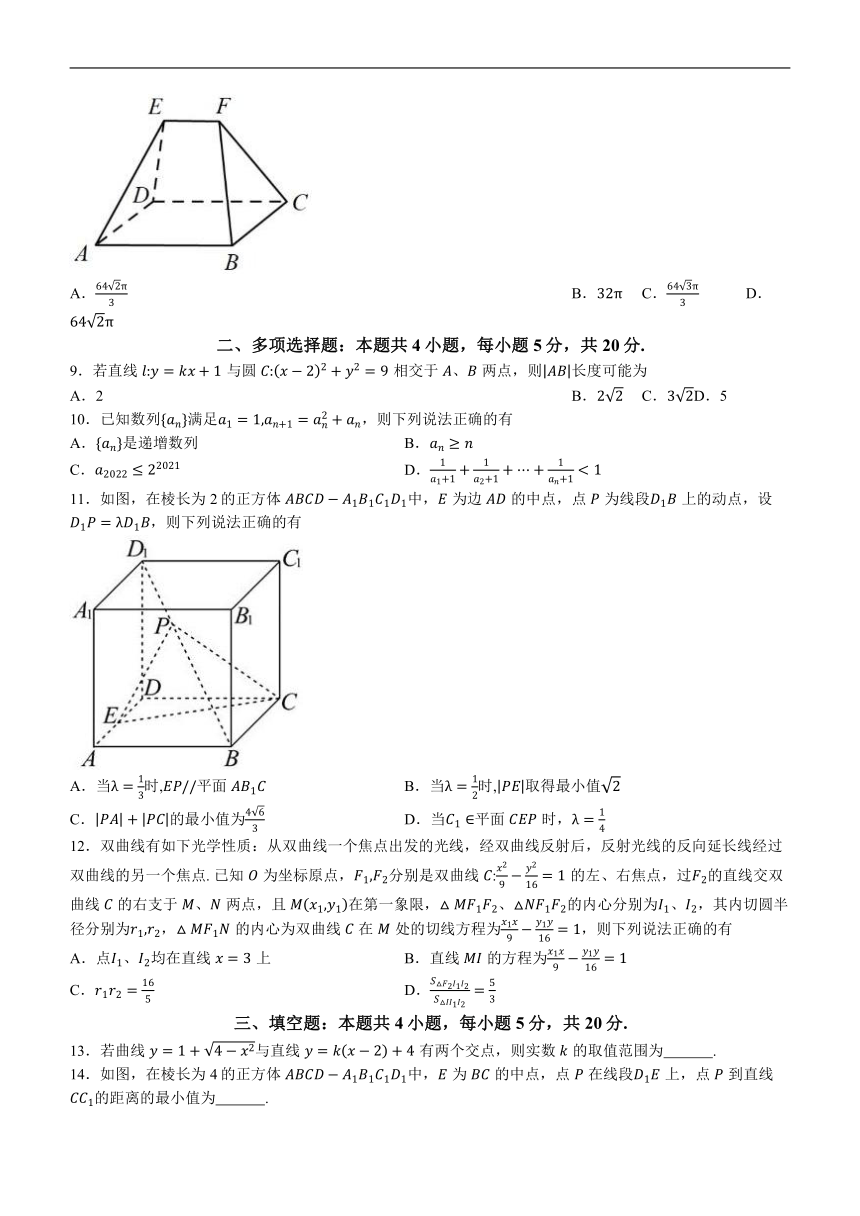
8.《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”. 现有一个刍甍如图所示,底面为正方形,底面,四边形,为两个全等的等腰梯形,,,则该刍甍的外接球的体积为
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.
9.若直线与圆相交于、两点,则长度可能为
A.2 B. C. D.5
10.已知数列满足,则下列说法正确的有
A.是递增数列 B.
C. D.
11.如图,在棱长为2的正方体中,为边的中点,点为线段上的动点,设,则下列说法正确的有
A.当时,平面 B.当时,取得最小值
C.的最小值为 D.当平面时,
12.双曲线有如下光学性质:从双曲线一个焦点出发的光线,经双曲线反射后,反射光线的反向延长线经过双曲线的另一个焦点. 已知为坐标原点,分别是双曲线:的左、右焦点,过的直线交双曲线的右支于两点,且在第一象限,的内心分别为,其内切圆半径分别为,的内心为双曲线在处的切线方程为,则下列说法正确的有
A.点均在直线上 B.直线的方程为
C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.若曲线与直线有两个交点,则实数的取值范围为 .
14.如图,在棱长为4的正方体中,为的中点,点在线段上,点到直线的距离的最小值为 .
15.斐波那契数列,又称黄金分割数列,被誉为最美数列,若数列满足,,则称数列为斐波事契数列,则 .
16.已知椭圆和双曲线的离心率分别为,且有公共的焦点,其中为左焦点,是与在第一象限的公共点. 若线段的垂直平分线经过坐标原点,则的最小值为 .
四、解答题:本题共6小题,共70分.
17.记数列的前项和为,且.
(1)求数列的通项公式;
(1)设为整数,且对,恒有,求的最小值.
18.已知圆与圆.
(1)证明:圆与圆相交;
(2)求两圆公共弦所在直线的方程;
(3)求经过两圆交点,且圆心在直线上的圆的方程.
19.双曲线的左顶点为,右焦点为,点为上一动点. 当时,.
(1)若点的坐标为,求双曲线的方程;
(2)若在第一象限,证明:.
20.已知直三棱柱中,侧面为正方形,,、分别为和的中点,为棱上的点. .
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小?
21.已知数列前项积为,且.
(1)求证:数列为等差数列;
(2)设,求证:.
22.阿基米德不仅是著名的哲学家、物理学家,也是著名的数学家. 他曾利用“逼近法”得到椭圆的面积等于圆周率、椭圆的长半轴长与短半轴长的乘积. 在直角坐标系中,椭圆的面积为,两焦点与短轴的一个顶点构成等边角形,过点且斜率不为0的直线与椭圆交于不同的两点、.
(1)求椭圆的标准方程;
(2)求面积的最大值;
(3)设椭圆的左、右顶点分别为、,直线与直线交于点,试问、、三点是否共线?若共线,请证明;若不共线,请说明理由.
一、单项选择题:本题共8小题,每小题5分,共40分.
1.已知不共线的三个空间向量,,,,则一定共线的三个点是
A.、、 B.、、 C.、、 D.、、
2.设直线与关于直线对称,则直线的方程是
A. B. C. D.
3.已知为等比数列,为数列的前项和,,则的值为
A.3 B.18 C.54 D.152
4.已知圆的方程为,点在直线上,线段为圆的直径,则的最小值为
A.2 B. C.3 D.
5.已知点是双曲线上的动点,为该双曲线的左右焦点,为坐标原点,则的最大值为
A. B.2 C. D.
6.若数列的通项公式是,则的值为
A. B. C. D.
7.如图所示,是双曲线的左右焦点,的右支上存在一点满足,与的左支的交点满足,则双曲线的离心率为
A.3 B. C. D.
8.《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”. 现有一个刍甍如图所示,底面为正方形,底面,四边形,为两个全等的等腰梯形,,,则该刍甍的外接球的体积为
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.
9.若直线与圆相交于、两点,则长度可能为
A.2 B. C. D.5
10.已知数列满足,则下列说法正确的有
A.是递增数列 B.
C. D.
11.如图,在棱长为2的正方体中,为边的中点,点为线段上的动点,设,则下列说法正确的有
A.当时,平面 B.当时,取得最小值
C.的最小值为 D.当平面时,
12.双曲线有如下光学性质:从双曲线一个焦点出发的光线,经双曲线反射后,反射光线的反向延长线经过双曲线的另一个焦点. 已知为坐标原点,分别是双曲线:的左、右焦点,过的直线交双曲线的右支于两点,且在第一象限,的内心分别为,其内切圆半径分别为,的内心为双曲线在处的切线方程为,则下列说法正确的有
A.点均在直线上 B.直线的方程为
C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.若曲线与直线有两个交点,则实数的取值范围为 .
14.如图,在棱长为4的正方体中,为的中点,点在线段上,点到直线的距离的最小值为 .
15.斐波那契数列,又称黄金分割数列,被誉为最美数列,若数列满足,,则称数列为斐波事契数列,则 .
16.已知椭圆和双曲线的离心率分别为,且有公共的焦点,其中为左焦点,是与在第一象限的公共点. 若线段的垂直平分线经过坐标原点,则的最小值为 .
四、解答题:本题共6小题,共70分.
17.记数列的前项和为,且.
(1)求数列的通项公式;
(1)设为整数,且对,恒有,求的最小值.
18.已知圆与圆.
(1)证明:圆与圆相交;
(2)求两圆公共弦所在直线的方程;
(3)求经过两圆交点,且圆心在直线上的圆的方程.
19.双曲线的左顶点为,右焦点为,点为上一动点. 当时,.
(1)若点的坐标为,求双曲线的方程;
(2)若在第一象限,证明:.
20.已知直三棱柱中,侧面为正方形,,、分别为和的中点,为棱上的点. .
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小?
21.已知数列前项积为,且.
(1)求证:数列为等差数列;
(2)设,求证:.
22.阿基米德不仅是著名的哲学家、物理学家,也是著名的数学家. 他曾利用“逼近法”得到椭圆的面积等于圆周率、椭圆的长半轴长与短半轴长的乘积. 在直角坐标系中,椭圆的面积为,两焦点与短轴的一个顶点构成等边角形,过点且斜率不为0的直线与椭圆交于不同的两点、.
(1)求椭圆的标准方程;
(2)求面积的最大值;
(3)设椭圆的左、右顶点分别为、,直线与直线交于点,试问、、三点是否共线?若共线,请证明;若不共线,请说明理由.
同课章节目录
