五年级上册数学苏教版2.8 组合图形的面积计算(课件)(共23张PPT)
文档属性
| 名称 | 五年级上册数学苏教版2.8 组合图形的面积计算(课件)(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 16:05:25 | ||
图片预览


文档简介
(共23张PPT)
组合图形的面积计算
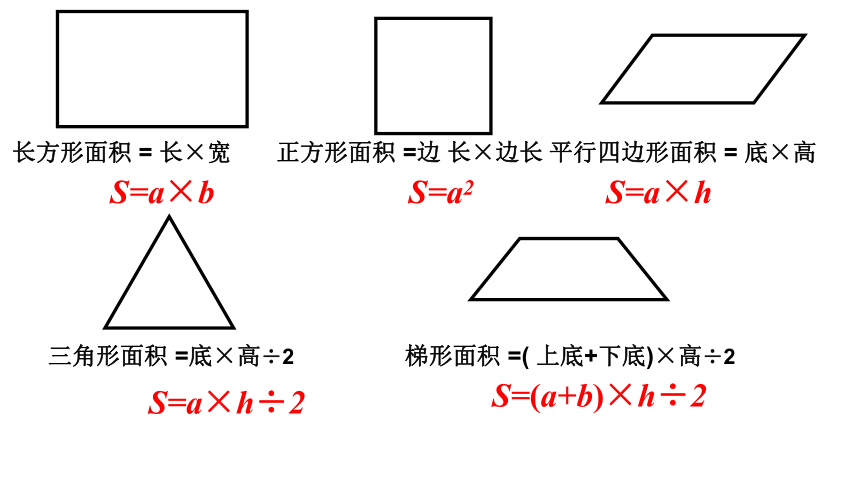
长方形面积 = 长×宽
正方形面积 =边 长×边长
三角形面积 =底×高÷2
平行四边形面积 = 底×高
梯形面积 =( 上底+下底)×高÷2
S=a×b
S=a2
S=a×h
S=a×h÷2
S=(a+b)×h÷2
你准备怎样算?与同学交流。
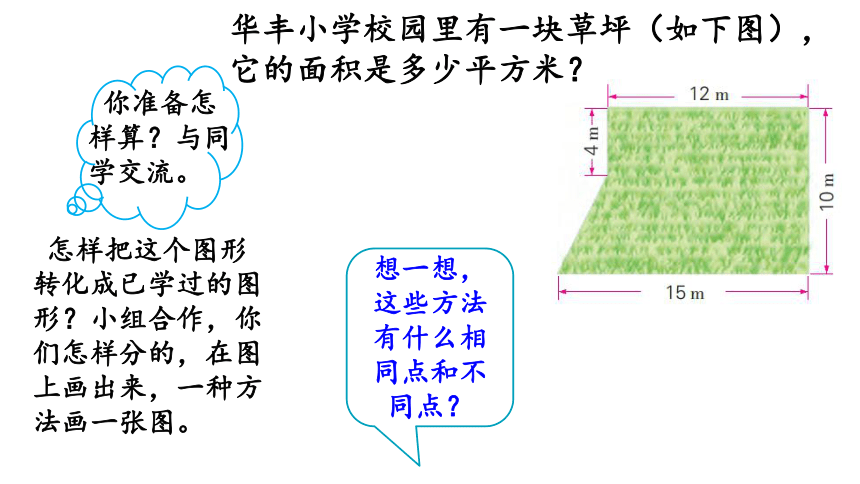
华丰小学校园里有一块草坪(如下图),它的面积是多少平方米?
怎样把这个图形转化成已学过的图形?小组合作,你们怎样分的,在图上画出来,一种方法画一张图。
想一想,这些方法有什么相同点和不同点?
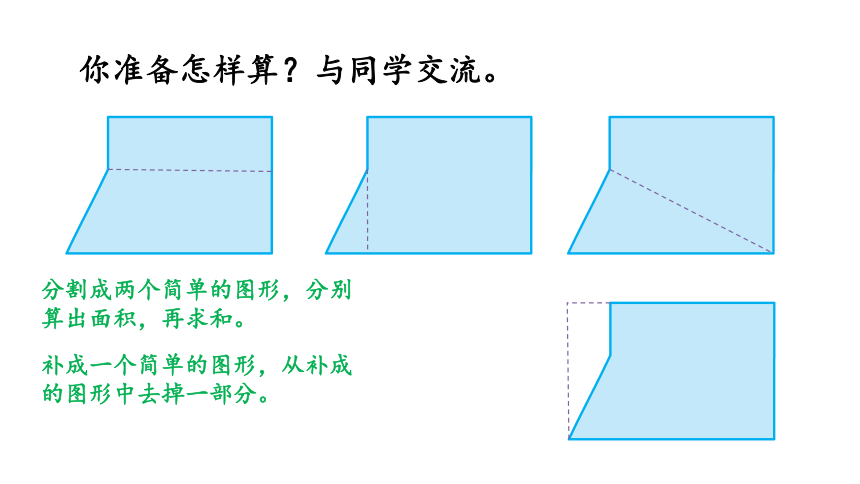
你准备怎样算?与同学交流。
分割成两个简单的图形,分别算出面积,再求和。
补成一个简单的图形,从补成的图形中去掉一部分。
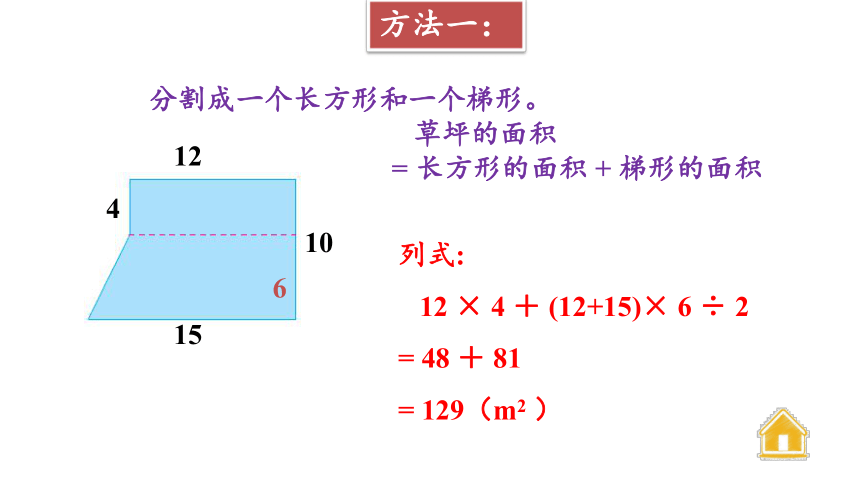
方法一:
列式:
12 × 4 + (12+15)× 6 ÷ 2
= 48 + 81
= 129(m2 )
12
15
4
10
分割成一个长方形和一个梯形。
6
草坪的面积
= 长方形的面积 + 梯形的面积
12
15
4
10
列式:
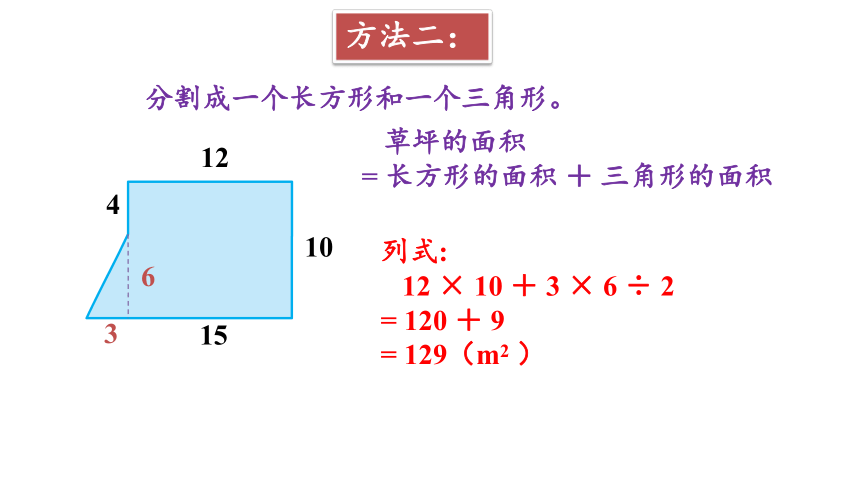
12 × 10 + 3 × 6 ÷ 2
= 120 + 9
= 129(m2 )
方法二:
分割成一个长方形和一个三角形。
6
3
草坪的面积
= 长方形的面积 + 三角形的面积
列式:
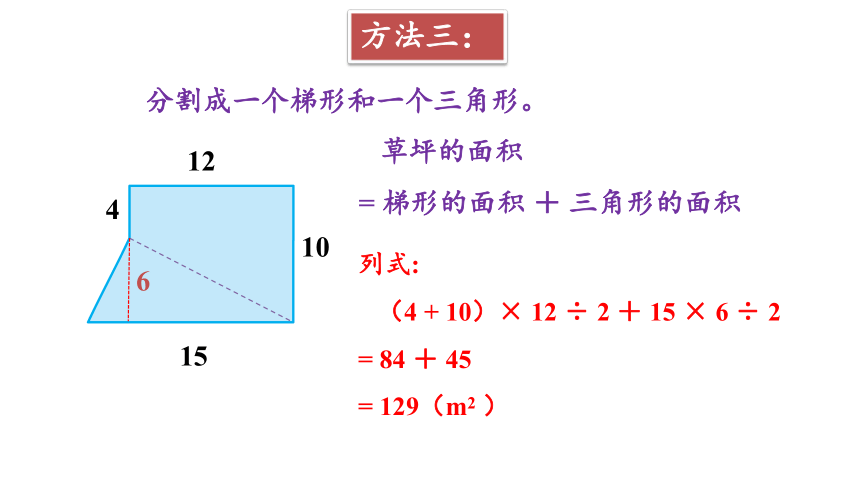
(4 + 10)× 12 ÷ 2 + 15 × 6 ÷ 2
= 84 + 45
= 129(m2 )
12
15
4
10
6
方法三:
分割成一个梯形和一个三角形。
草坪的面积
= 梯形的面积 + 三角形的面积
列式:
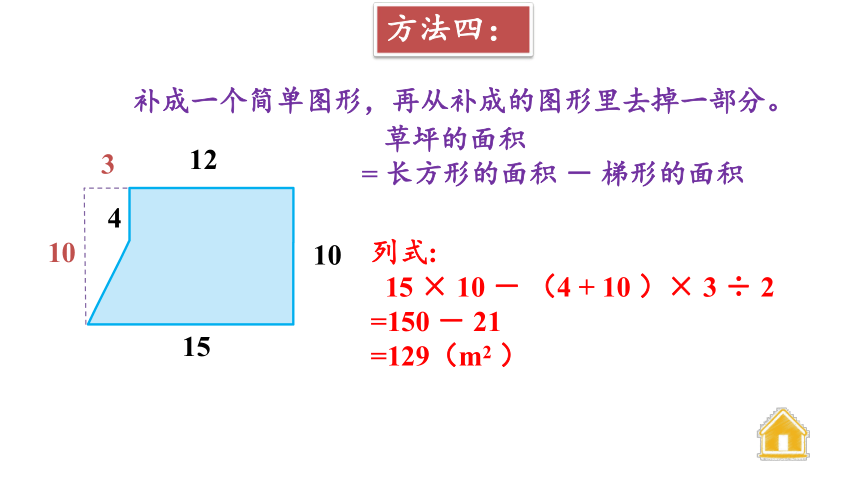
15 × 10 - (4 + 10 )× 3 ÷ 2
=150 - 21
=129(m2 )
方法四:
12
15
4
10
10
3
补成一个简单图形,再从补成的图形里去掉一部分。
草坪的面积
= 长方形的面积 - 梯形的面积
图形内:分割法 求和
图形外:添补法 求差
在进行图形的割补时,要注意什么?
要便于利用已知条件计算简单图形的面积。
要根据原来图形的特点进行思考。
可以用不同的方法进行割补。
练一练 :校园里有一块花圃(如下图),你能算出它的面积是多少平方米吗?
怎样把这个图形转化成已学过的图形?
分割法
添补法
计算组合图形的面积主要可以采用
“分割” 与“添补”的方法进行计算。
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6×2 + 4×3
= 12 + 12
= 24(m2)
4×5+2×2
= 20 + 4
= 24(m2)
方法一:分割成两个长方形
方法二:分割成一个长方形和一个正方形
5—2=3(m)
答:至少要24平方米的地板。
答:至少要24平方米的地板。
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
(3+5)×4÷2 + (2+6)×2÷2
= 8×4÷2 + 8×2÷2
= 24(m2)
6×5 —2×3
= 30—6
= 24(m2)
方法三:分割成两个梯形
方法四:补上一个小长方形,使它成为一个大长方形
6—4=2(m)
3m
2m
2m
3m
答:至少要24平方米的地板。
答:至少要24平方米的地板。
1.求下面图形的面积。(单位:cm)
【教材第23页 练习四 】
梯形:(40 + 20)× 10 ÷ 2
= 30× 10
=300(cm2)
正方形: 20 × 20=400(cm2)
共:300+400= 700(cm2)
三角形:20×9 ÷ 2=90(cm2)
平行四边形:12 × 16=192(cm2)
共:90+192= 282(cm2)
梯形:(6 +10)× 2 ÷ 2=16(cm2)
长方形: 10 × 8=80(cm2)
阴影:80-16= 64(cm2)
2.绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如图),草坪的面积是多少平方米?
答:草坪的面积是512平方米。
梯形: (20+36 ) ×20÷2
= 56×10
= 560(m2)
长方形: 12 × 4=48(m2)
阴影:560-48=512(cm2)
求下图阴影部分的面积
4
三角形面积:4×4÷2=8(cm2)
学以致用
8 × 8 + 5 × 5 – 8 ×(8 + 5)÷ 2
= 64 + 25 – 52
= 37(cm2)
(8 + 5) × 8 ÷ 2 – 5 ×(8 – 5)
= 52 – 15
= 37 (cm2)
4. 如图,有两个边长是8cm的正方形卡片叠在一起,求重叠部分的面积。(单位:cm)
(8 - 4)×(8 - 4)
= 4 × 4
= 16(cm2)
答:重叠部分的面积是16cm2。
3. 如图,一张硬纸板剪下4个边长是4cm的小正方形后,可以做成一个没有盖子的盒子。你知道剪后的硬纸板面积是多少吗?
26 × 20 – 4 × 4 × 4
= 520 - 64
= 456(cm2)
答:剪后的硬纸板面积是456cm2。
这节课你们都学会了哪些知识?
课堂小结
1.计算组合图形的面积主要可以采用“分割”与“添补”的方法进行计算。
2.分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
3.添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
组合图形的面积计算
长方形面积 = 长×宽
正方形面积 =边 长×边长
三角形面积 =底×高÷2
平行四边形面积 = 底×高
梯形面积 =( 上底+下底)×高÷2
S=a×b
S=a2
S=a×h
S=a×h÷2
S=(a+b)×h÷2
你准备怎样算?与同学交流。
华丰小学校园里有一块草坪(如下图),它的面积是多少平方米?
怎样把这个图形转化成已学过的图形?小组合作,你们怎样分的,在图上画出来,一种方法画一张图。
想一想,这些方法有什么相同点和不同点?
你准备怎样算?与同学交流。
分割成两个简单的图形,分别算出面积,再求和。
补成一个简单的图形,从补成的图形中去掉一部分。
方法一:
列式:
12 × 4 + (12+15)× 6 ÷ 2
= 48 + 81
= 129(m2 )
12
15
4
10
分割成一个长方形和一个梯形。
6
草坪的面积
= 长方形的面积 + 梯形的面积
12
15
4
10
列式:
12 × 10 + 3 × 6 ÷ 2
= 120 + 9
= 129(m2 )
方法二:
分割成一个长方形和一个三角形。
6
3
草坪的面积
= 长方形的面积 + 三角形的面积
列式:
(4 + 10)× 12 ÷ 2 + 15 × 6 ÷ 2
= 84 + 45
= 129(m2 )
12
15
4
10
6
方法三:
分割成一个梯形和一个三角形。
草坪的面积
= 梯形的面积 + 三角形的面积
列式:
15 × 10 - (4 + 10 )× 3 ÷ 2
=150 - 21
=129(m2 )
方法四:
12
15
4
10
10
3
补成一个简单图形,再从补成的图形里去掉一部分。
草坪的面积
= 长方形的面积 - 梯形的面积
图形内:分割法 求和
图形外:添补法 求差
在进行图形的割补时,要注意什么?
要便于利用已知条件计算简单图形的面积。
要根据原来图形的特点进行思考。
可以用不同的方法进行割补。
练一练 :校园里有一块花圃(如下图),你能算出它的面积是多少平方米吗?
怎样把这个图形转化成已学过的图形?
分割法
添补法
计算组合图形的面积主要可以采用
“分割” 与“添补”的方法进行计算。
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
6×2 + 4×3
= 12 + 12
= 24(m2)
4×5+2×2
= 20 + 4
= 24(m2)
方法一:分割成两个长方形
方法二:分割成一个长方形和一个正方形
5—2=3(m)
答:至少要24平方米的地板。
答:至少要24平方米的地板。
6 m
2 m
5 m
4 m
6 m
2 m
5 m
4 m
(3+5)×4÷2 + (2+6)×2÷2
= 8×4÷2 + 8×2÷2
= 24(m2)
6×5 —2×3
= 30—6
= 24(m2)
方法三:分割成两个梯形
方法四:补上一个小长方形,使它成为一个大长方形
6—4=2(m)
3m
2m
2m
3m
答:至少要24平方米的地板。
答:至少要24平方米的地板。
1.求下面图形的面积。(单位:cm)
【教材第23页 练习四 】
梯形:(40 + 20)× 10 ÷ 2
= 30× 10
=300(cm2)
正方形: 20 × 20=400(cm2)
共:300+400= 700(cm2)
三角形:20×9 ÷ 2=90(cm2)
平行四边形:12 × 16=192(cm2)
共:90+192= 282(cm2)
梯形:(6 +10)× 2 ÷ 2=16(cm2)
长方形: 10 × 8=80(cm2)
阴影:80-16= 64(cm2)
2.绿波小区有一块梯形草坪,草坪的中间有一个长方形的花坛(如图),草坪的面积是多少平方米?
答:草坪的面积是512平方米。
梯形: (20+36 ) ×20÷2
= 56×10
= 560(m2)
长方形: 12 × 4=48(m2)
阴影:560-48=512(cm2)
求下图阴影部分的面积
4
三角形面积:4×4÷2=8(cm2)
学以致用
8 × 8 + 5 × 5 – 8 ×(8 + 5)÷ 2
= 64 + 25 – 52
= 37(cm2)
(8 + 5) × 8 ÷ 2 – 5 ×(8 – 5)
= 52 – 15
= 37 (cm2)
4. 如图,有两个边长是8cm的正方形卡片叠在一起,求重叠部分的面积。(单位:cm)
(8 - 4)×(8 - 4)
= 4 × 4
= 16(cm2)
答:重叠部分的面积是16cm2。
3. 如图,一张硬纸板剪下4个边长是4cm的小正方形后,可以做成一个没有盖子的盒子。你知道剪后的硬纸板面积是多少吗?
26 × 20 – 4 × 4 × 4
= 520 - 64
= 456(cm2)
答:剪后的硬纸板面积是456cm2。
这节课你们都学会了哪些知识?
课堂小结
1.计算组合图形的面积主要可以采用“分割”与“添补”的方法进行计算。
2.分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
3.添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
