第八章 平行线的有关证明 6 三角形内角和定理 第2课时 三角形的外角(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 6 三角形内角和定理 第2课时 三角形的外角(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
6 三角形内角和定理
第2课时 三角形的外角
基 础 练
知识点一 三角形的一个外角等于和它不相邻的两个内角的和
1.如图,在 中,点D 在 BC 的 延 长线 上,若 ∠B=45°,则∠A的度数为 ( )
A.45° B.53° C.63° D.65°
第1 题图 第 2 题图
2.如图,AB∥CD,点E 在BC 上,若 ,则∠3 的度数是 ( )
A.60° B.70° C.80° D.50°
3.一副直角三角板如图放置,点C 在FD 的延长线上, 则
第 3 题图 第 4 题图
4.如图,平面上直线 a,b分别经过线段OK 两端点(数据如图),则a,b相交所成的锐角是___________.
5.如图,在 中, 求 的度数.
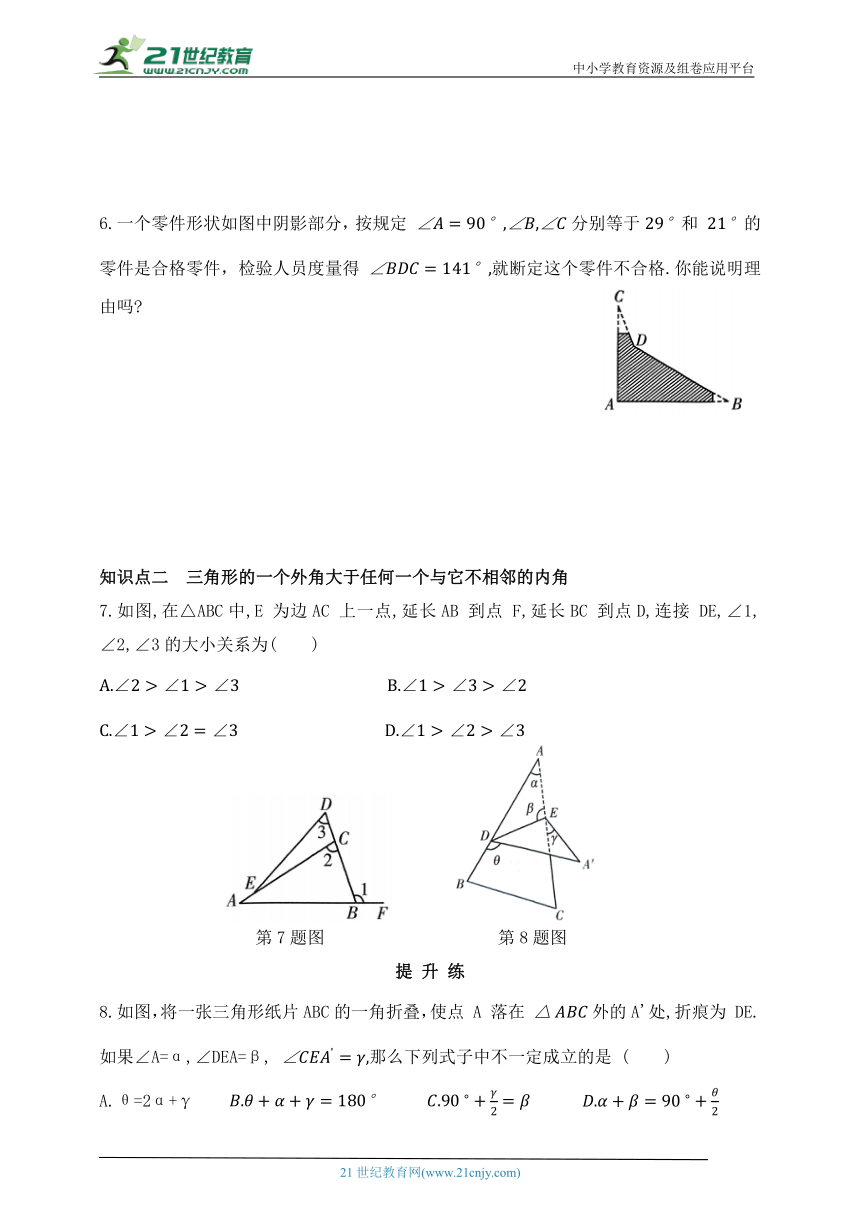
6.一个零件形状如图中阴影部分,按规定 分别等于和 的零件是合格零件,检验人员度量得 就断定这个零件不合格.你能说明理由吗
知识点二 三角形的一个外角大于任何一个与它不相邻的内角
7.如图,在△ABC中,E 为边AC 上一点,延长AB 到点 F,延长BC 到点D,连接 DE,∠1, ∠2,∠3的大小关系为( )
第7题图 第8题图
提 升 练
8.如图,将一张三角形纸片ABC的一角折叠,使点 A 落在 外的A'处,折痕为 DE. 如果∠A=α,∠DEA=β, 那么下列式子中不一定成立的是 ( )
A.θ=2α+γ
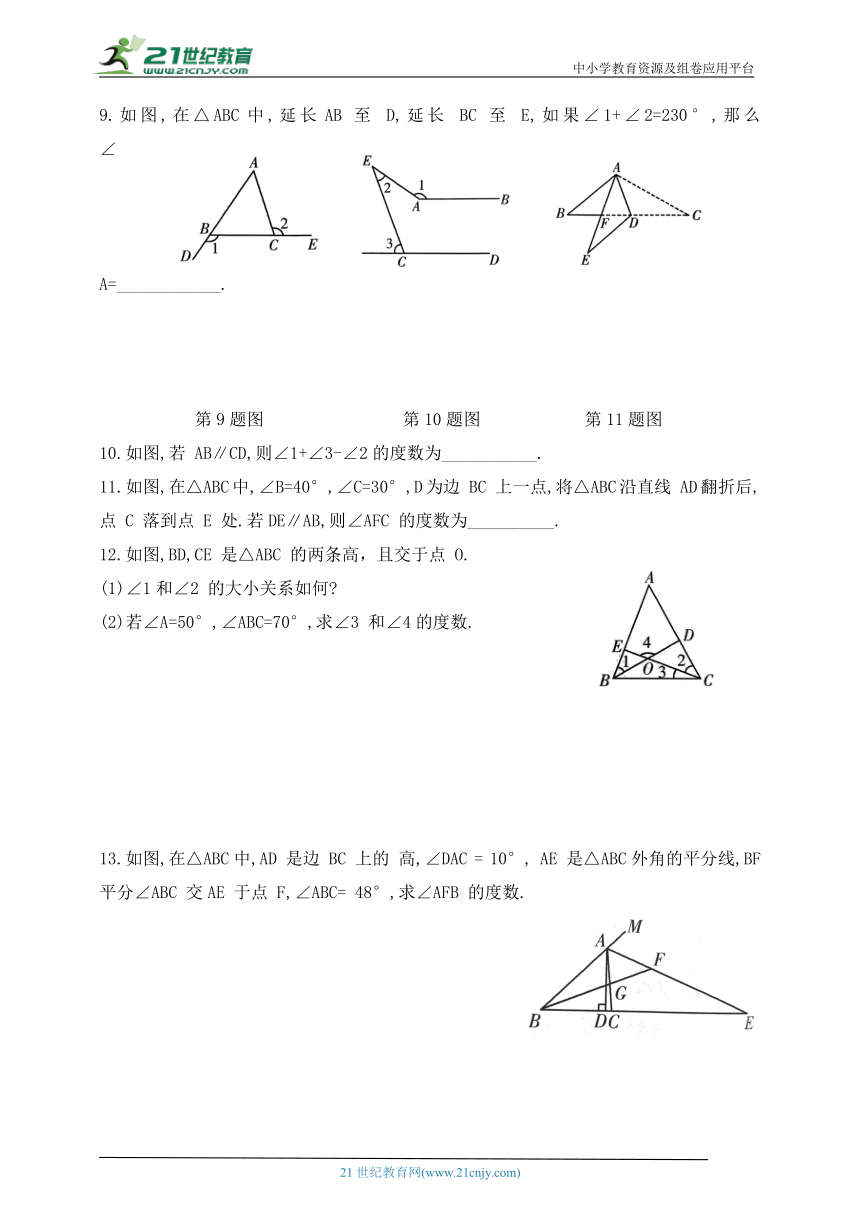
9.如图,在△ABC中,延长AB 至 D,延长 BC 至 E,如果∠1+∠2=230°,那么 ∠A=____________.
第9题图 第10题图 第11题图
10.如图,若 AB∥CD,则∠1+∠3-∠2的度数为___________.
11.如图,在△ABC中,∠B=40°,∠C=30°,D为边 BC 上一点,将△ABC沿直线 AD翻折后,点 C 落到点 E 处.若DE∥AB,则∠AFC 的度数为__________.
12.如图,BD,CE 是△ABC 的两条高,且交于点 O.
(1)∠1和∠2 的大小关系如何
(2)若∠A=50°,∠ABC=70°,求∠3 和∠4的度数.
13.如图,在△ABC中,AD 是边 BC 上的 高,∠DAC = 10°, AE 是△ABC外角的平分线,BF 平分∠ABC 交AE 于点 F,∠ABC= 48°,求∠AFB 的度数.
14.数学兴趣小组学习了三角形的外角性质 1:三角形的一个外角等于与它不相邻的两个内角和. 提出问题:四边形的一个外角与它不相邻的内角之和具有怎样的数量关系
(1)【回顾】如图 1.请直接写出∠ACD与∠A,∠B之间的数量关系:_____________;
(2)【探究】如图 2,已知∠DCE 是四边形ABCD 的外角,求∠DCE,∠A,∠B与∠D 的数量关系.请补全下面解答过程.
解:∵∠DCE是四边形ABCD的外角,∴∠DCE+__________=180°,
∵∠DCB+∠B+∠D+∠A=__________,__________,
∴∠DCE=∠A+∠B+∠D+_____________.
参考答案
1. C 2. A 3.15 4.30°
5.解:∵∠1=∠2,∠3=∠4,∴∠4=2∠1=2∠2=∠3,
∴∠2+∠3=3∠2=126°,∴∠2=∠1=42°,
∴∠DAC=54°-42°=12°.
6.解:理由是:如图,延长BD交 AC 于E 点,
根据三角形的外角性质可知,∠CED=∠A+∠B,∠BDC=∠CED+∠C,
∴∠BDC=∠A+∠B+∠C=90°+29°+21°=140°,
所以检验人员度量得∠BDC=141°,可断定这个零件不合格.
7. D 8. B 9 .50° 10.180° 11.70°
12.解:(1)∵BD,CE是△ABC的两条高,∴∠BEO=∠CDO=90°.
∵∠4=∠BEO+∠1=∠CDO+∠2,∴∠1=∠2.
(2)由三角形内角和定理得
∠3=180°-∠BEC-∠ABC=180°-90°-70°=20°,
∠2=180°-∠A-∠AEC=180°-50°-90°=40°,
∴∠4=∠ODC+∠2=90°+40°=130°.
13.解:∵AD是边BC 上的高,∴∠ADB=90°,∴∠BAD=90°-∠ABC=42°.
又∵∠DAC=10°,∴∠BAC=52°,∴∠MAC=180°-∠BAC=128°.
∵AE 是△ABC外角的平分线,
∵BF平分
∴∠AFB=∠MAE-∠ABF=40°.
14.解:(1)∠ACD=∠A+∠B
(2)∵∠DCE是四边形ABCD 的外角,∴∠DCE+∠DCB=180°,
∴∠DCB=180°-∠DCE.
∵∠DCB+∠B+∠D+∠A=360°,∴180°-∠DCE+∠A+∠B+∠D=360°,
∴∠DCE=∠A+∠B+∠D+(-180°).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
6 三角形内角和定理
第2课时 三角形的外角
基 础 练
知识点一 三角形的一个外角等于和它不相邻的两个内角的和
1.如图,在 中,点D 在 BC 的 延 长线 上,若 ∠B=45°,则∠A的度数为 ( )
A.45° B.53° C.63° D.65°
第1 题图 第 2 题图
2.如图,AB∥CD,点E 在BC 上,若 ,则∠3 的度数是 ( )
A.60° B.70° C.80° D.50°
3.一副直角三角板如图放置,点C 在FD 的延长线上, 则
第 3 题图 第 4 题图
4.如图,平面上直线 a,b分别经过线段OK 两端点(数据如图),则a,b相交所成的锐角是___________.
5.如图,在 中, 求 的度数.
6.一个零件形状如图中阴影部分,按规定 分别等于和 的零件是合格零件,检验人员度量得 就断定这个零件不合格.你能说明理由吗
知识点二 三角形的一个外角大于任何一个与它不相邻的内角
7.如图,在△ABC中,E 为边AC 上一点,延长AB 到点 F,延长BC 到点D,连接 DE,∠1, ∠2,∠3的大小关系为( )
第7题图 第8题图
提 升 练
8.如图,将一张三角形纸片ABC的一角折叠,使点 A 落在 外的A'处,折痕为 DE. 如果∠A=α,∠DEA=β, 那么下列式子中不一定成立的是 ( )
A.θ=2α+γ
9.如图,在△ABC中,延长AB 至 D,延长 BC 至 E,如果∠1+∠2=230°,那么 ∠A=____________.
第9题图 第10题图 第11题图
10.如图,若 AB∥CD,则∠1+∠3-∠2的度数为___________.
11.如图,在△ABC中,∠B=40°,∠C=30°,D为边 BC 上一点,将△ABC沿直线 AD翻折后,点 C 落到点 E 处.若DE∥AB,则∠AFC 的度数为__________.
12.如图,BD,CE 是△ABC 的两条高,且交于点 O.
(1)∠1和∠2 的大小关系如何
(2)若∠A=50°,∠ABC=70°,求∠3 和∠4的度数.
13.如图,在△ABC中,AD 是边 BC 上的 高,∠DAC = 10°, AE 是△ABC外角的平分线,BF 平分∠ABC 交AE 于点 F,∠ABC= 48°,求∠AFB 的度数.
14.数学兴趣小组学习了三角形的外角性质 1:三角形的一个外角等于与它不相邻的两个内角和. 提出问题:四边形的一个外角与它不相邻的内角之和具有怎样的数量关系
(1)【回顾】如图 1.请直接写出∠ACD与∠A,∠B之间的数量关系:_____________;
(2)【探究】如图 2,已知∠DCE 是四边形ABCD 的外角,求∠DCE,∠A,∠B与∠D 的数量关系.请补全下面解答过程.
解:∵∠DCE是四边形ABCD的外角,∴∠DCE+__________=180°,
∵∠DCB+∠B+∠D+∠A=__________,__________,
∴∠DCE=∠A+∠B+∠D+_____________.
参考答案
1. C 2. A 3.15 4.30°
5.解:∵∠1=∠2,∠3=∠4,∴∠4=2∠1=2∠2=∠3,
∴∠2+∠3=3∠2=126°,∴∠2=∠1=42°,
∴∠DAC=54°-42°=12°.
6.解:理由是:如图,延长BD交 AC 于E 点,
根据三角形的外角性质可知,∠CED=∠A+∠B,∠BDC=∠CED+∠C,
∴∠BDC=∠A+∠B+∠C=90°+29°+21°=140°,
所以检验人员度量得∠BDC=141°,可断定这个零件不合格.
7. D 8. B 9 .50° 10.180° 11.70°
12.解:(1)∵BD,CE是△ABC的两条高,∴∠BEO=∠CDO=90°.
∵∠4=∠BEO+∠1=∠CDO+∠2,∴∠1=∠2.
(2)由三角形内角和定理得
∠3=180°-∠BEC-∠ABC=180°-90°-70°=20°,
∠2=180°-∠A-∠AEC=180°-50°-90°=40°,
∴∠4=∠ODC+∠2=90°+40°=130°.
13.解:∵AD是边BC 上的高,∴∠ADB=90°,∴∠BAD=90°-∠ABC=42°.
又∵∠DAC=10°,∴∠BAC=52°,∴∠MAC=180°-∠BAC=128°.
∵AE 是△ABC外角的平分线,
∵BF平分
∴∠AFB=∠MAE-∠ABF=40°.
14.解:(1)∠ACD=∠A+∠B
(2)∵∠DCE是四边形ABCD 的外角,∴∠DCE+∠DCB=180°,
∴∠DCB=180°-∠DCE.
∵∠DCB+∠B+∠D+∠A=360°,∴180°-∠DCE+∠A+∠B+∠D=360°,
∴∠DCE=∠A+∠B+∠D+(-180°).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
