第八章 平行线的有关证明 单元测试卷(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明 单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 09:13:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章 平行线的有关证明
单元测试卷
(时间:120分钟 总分:150 分)
一、选择题(本大题共 12 小题,每小题 4 分,满分 48 分)
1.下列语句中,属于定义的是 ( )
A.对顶角相等
B.作一条直线和已知直线垂直
C.在同一平面内,不相交的两条直线叫做平行线
D.图形的平移不改变图形的形状和大小
2.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是 ( )
A.∠1=∠2=45° B.∠1=50°,∠2=50°
C.∠1=50°,∠2=40° D.∠1=40°,∠2=40°
3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小是( )
A.65° B.55° C.45° D.35°
4.给出下列命题:①三角形的一个外角一定大于它的一个内角;②若一个三角形的三个内角的度数之比为1: 3:4,则它肯定是直角三角形;③三角形的最小内角不能大于 60°;④三角形的一个外角等于和它不相邻的两个内角的和.其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
5.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定 AB∥CD的条件有 ( )
A.1个 B.2个 C.3个 D.4个
第5题图 第6题图
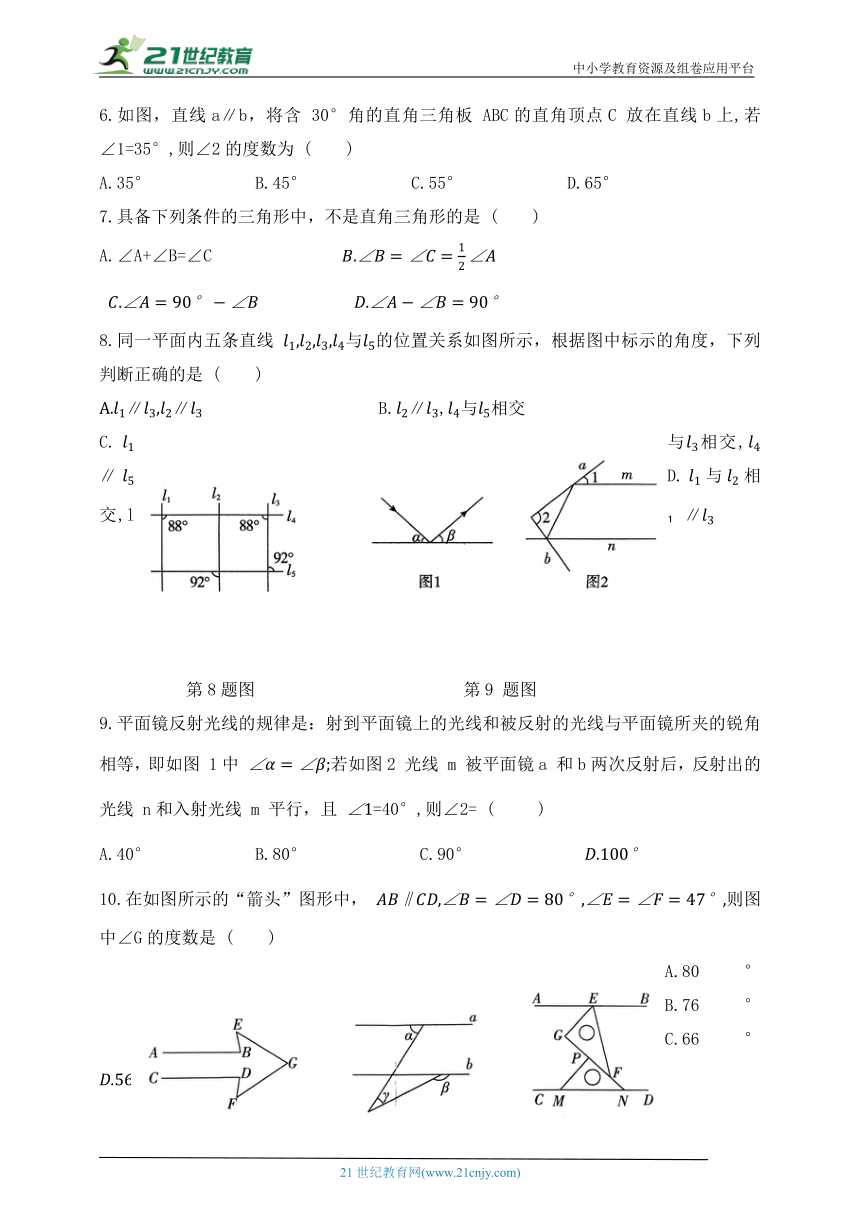
6.如图,直线a∥b,将含 30°角的直角三角板 ABC的直角顶点C 放在直线b上,若 ∠1=35°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
7.具备下列条件的三角形中,不是直角三角形的是 ( )
A.∠A+∠B=∠C
8.同一平面内五条直线 与的位置关系如图所示,根据图中标示的角度,下列判断正确的是 ( )
∥∥B.∥,与相交
C.与相交,∥ D.与相交,l ∥
第8题图 第9 题图
9.平面镜反射光线的规律是:射到平面镜上的光线和被反射的光线与平面镜所夹的锐角相等,即如图 1中 若如图2 光线 m 被平面镜a 和b两次反射后,反射出的光线 n和入射光线 m 平行,且 =40°,则∠2= ( )
A.40° B.80° C.90°
10.在如图所示的“箭头”图形中, 则图中∠G的度数是 ( )
A.80° B.76° C.66°
第 10 题图 第11题图 第12题图
11.如图所示,a∥b,则下列式子中,值为 180°的是 ( )
A.∠α+∠β-∠γ B.∠α+∠β+∠γ
C.∠β+∠γ-∠α D.∠α-∠β+∠γ
12.如图,AB∥CD,将一副直角三角板作如下摆放,∠GEF=60°, ∠MNP=45°.下列结论: ①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共 6 小题,每小题4 分,满分 24 分)
13.把命题“等角的余角相等”写成“如果……,那么……”的形式为______________________________________________.
14.在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理_______________________.
第14 题图 第15题图 第 16 题图
15.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=130°,第二次拐角∠B=150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 为__________度.
16.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACF=____________.
17.如图,在△ABC中,∠A=60°,∠ABC和∠ACD的平分线交于点A ,得∠A ,∠A BC和∠A CD的平分线交于点A ,得∠A ,则∠ ___________度.
第17 题图 第18 题图
18.如图,
三、解答题(本大题共7 小题,满分78 分)
19.(10分)如图,现有以下 3 个论断:①AB∥CD;②∠B=∠C;③∠E 请以其中2 个论断为条件,另一个论断为结论构造命题.
(1)你构造的是哪几个命题
(2)请选择其中一个真命题加以证明.
20.(10分)人们常用装了水的玻璃杯检查桌子是否水平,从侧面看的结果如图所示.(注:杯子底是平的,而且上下粗细均匀)
(1)若 能说明桌面水平吗 为什么
(2)若 能说明桌面水平吗 为什么
21.(10分)如图,在△ABC中,CD⊥AB 于点D,DE∥BC 交 AC 于点E,EF⊥CD 于点G,交 BC 于点 F.
(1)判断∠ADE 与∠EFC 是否相等,并说明理由;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
22.(10分)如图,已知BC∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若 AQ平分∠FAC,交 BC 于点Q,且∠Q=15°,求∠ACQ的度数.
23.(12 分)如图,在折纸活动中,小李制作了一张 的纸片,点 D, E 分别在边AB,AC 上,将 沿着 DE 折叠压平,A 与 重合.
(1)若 求 的度数;
(2)若 求 的度数.
24.(12分)已知一个角的两边与另一个角的两边分别平行,请结合图形回答下列问题:
(1)如图1,AB∥CD,BE∥DF,直接写出∠1与∠2的关系___________;
(2)如图 2,AB∥CD,BE∥DF,猜想∠1 与∠2 的关系,并说明理由;
(3)由(1)(2),我们可以得出结论:一个角的两边与另一个角的两边分别平行,那么这两个角_______________;
(4)应用:两个角的两边分别平行,且一个角比另一个角的 3 倍少60°,求这两个角的度数.
25.(14 分)【问题背景】∠MON=90°,点 A,B分别在OM,ON上运动(不与点O 重合).
图1 图2 图3
(1)【问题思考】如图1,AE,BE分别是∠BAO和∠ABO的平分线,随着点 A、点 B的运动,∠AEB=__________.
(2)如图2,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D=___________°.
②随着点A,B的运动,∠D的大小会变吗 如果不会,求∠D 的度数;如果会,请说明理由.
(3)【问题拓展】在图 2 的基础上,如果∠MON=α,其余条件不变,随着点A,B的运动(如图3),∠D=___________.(用含α的代数式表示)
参考答案
1. C 2. A 3. B 4. C 5. C 6. C 7. D 8. B 9. C 10. C
11. A 12. D
13.如果两个角相等,那么这两个角的余角相等
14.三角形的内角和是
15.160
17.15
19.解:(1)由①②得③;由①③得②;由②③得①.
(2)由①②,得③.
∥
又∵ ∥
20.解:(1)不能.
理由: ∥CD,即AE∥CF.
AE,CF都不是桌面或水平面,故不能说明桌面水平.
(2)能.理由:∵EF⊥CF,BD⊥CF,∴BD∥EF(在同一个平面内,垂直于同一条直线的两直线平行).∴能说明桌面是水平的.
21.解:(1)∠ADE=∠EFC,
理由:∵DE∥BC,∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,∴AB∥EF,∴∠B=∠EFC,
∴∠ADE=∠EFC.
(2)∵∠ACB=72°,∠A=60°,∴∠B=180°-∠A-∠ACB=48°,
∵CD⊥AB,∴∠BDC=90°,
∴∠DCB=180°-90°-48°=42°.
22.(1)证明:∵BC∥GE,∴∠E=∠1=50°,
∵∠AFG=∠1=50°,∴∠E=∠AFG=50°,∴AF∥DE.
(2)解:∵∠1=50°,∠Q=15°,∴∠AHD=∠1+∠Q=65°,
∵AF∥DE,∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°-∠CAQ-∠Q=100°.
23.解:(1)∵∠A+∠B+∠C=180°,
∴∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)∵△A'DE 是△ABC翻折变换而成,∴∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
∴∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A,
24.(1)∠1=∠2
(2)解:∠1+∠2=180°.理由如下:
∵AB∥CD,∴∠1=∠3,
∵BE∥DF,∴∠2+∠3=180°,∴∠1+∠2=180°.
(3)相等或互补
(4)解:设一个角的度数为x,则另一个角的度数为3x-60°,
当x=3x-60°,解得 x=30°,则这两个角的度数分别为30°,30°;
当x+3x-60°=180°,解得x=60°,则这两个角的度数分别为 60°,120°.
综上所述,这两个角的度数分别为 30°,30°或60°,120°.
25.(1)135°
(2)①45
②解: 的度数不随点 A,B的移动而发生变化,设
∵AD平分
∵BC 平分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 平行线的有关证明
单元测试卷
(时间:120分钟 总分:150 分)
一、选择题(本大题共 12 小题,每小题 4 分,满分 48 分)
1.下列语句中,属于定义的是 ( )
A.对顶角相等
B.作一条直线和已知直线垂直
C.在同一平面内,不相交的两条直线叫做平行线
D.图形的平移不改变图形的形状和大小
2.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是 ( )
A.∠1=∠2=45° B.∠1=50°,∠2=50°
C.∠1=50°,∠2=40° D.∠1=40°,∠2=40°
3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小是( )
A.65° B.55° C.45° D.35°
4.给出下列命题:①三角形的一个外角一定大于它的一个内角;②若一个三角形的三个内角的度数之比为1: 3:4,则它肯定是直角三角形;③三角形的最小内角不能大于 60°;④三角形的一个外角等于和它不相邻的两个内角的和.其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
5.如图,给出下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定 AB∥CD的条件有 ( )
A.1个 B.2个 C.3个 D.4个
第5题图 第6题图
6.如图,直线a∥b,将含 30°角的直角三角板 ABC的直角顶点C 放在直线b上,若 ∠1=35°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
7.具备下列条件的三角形中,不是直角三角形的是 ( )
A.∠A+∠B=∠C
8.同一平面内五条直线 与的位置关系如图所示,根据图中标示的角度,下列判断正确的是 ( )
∥∥B.∥,与相交
C.与相交,∥ D.与相交,l ∥
第8题图 第9 题图
9.平面镜反射光线的规律是:射到平面镜上的光线和被反射的光线与平面镜所夹的锐角相等,即如图 1中 若如图2 光线 m 被平面镜a 和b两次反射后,反射出的光线 n和入射光线 m 平行,且 =40°,则∠2= ( )
A.40° B.80° C.90°
10.在如图所示的“箭头”图形中, 则图中∠G的度数是 ( )
A.80° B.76° C.66°
第 10 题图 第11题图 第12题图
11.如图所示,a∥b,则下列式子中,值为 180°的是 ( )
A.∠α+∠β-∠γ B.∠α+∠β+∠γ
C.∠β+∠γ-∠α D.∠α-∠β+∠γ
12.如图,AB∥CD,将一副直角三角板作如下摆放,∠GEF=60°, ∠MNP=45°.下列结论: ①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本大题共 6 小题,每小题4 分,满分 24 分)
13.把命题“等角的余角相等”写成“如果……,那么……”的形式为______________________________________________.
14.在我们的生活中处处有数学的身影,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理_______________________.
第14 题图 第15题图 第 16 题图
15.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=130°,第二次拐角∠B=150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 为__________度.
16.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACF=____________.
17.如图,在△ABC中,∠A=60°,∠ABC和∠ACD的平分线交于点A ,得∠A ,∠A BC和∠A CD的平分线交于点A ,得∠A ,则∠ ___________度.
第17 题图 第18 题图
18.如图,
三、解答题(本大题共7 小题,满分78 分)
19.(10分)如图,现有以下 3 个论断:①AB∥CD;②∠B=∠C;③∠E 请以其中2 个论断为条件,另一个论断为结论构造命题.
(1)你构造的是哪几个命题
(2)请选择其中一个真命题加以证明.
20.(10分)人们常用装了水的玻璃杯检查桌子是否水平,从侧面看的结果如图所示.(注:杯子底是平的,而且上下粗细均匀)
(1)若 能说明桌面水平吗 为什么
(2)若 能说明桌面水平吗 为什么
21.(10分)如图,在△ABC中,CD⊥AB 于点D,DE∥BC 交 AC 于点E,EF⊥CD 于点G,交 BC 于点 F.
(1)判断∠ADE 与∠EFC 是否相等,并说明理由;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
22.(10分)如图,已知BC∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若 AQ平分∠FAC,交 BC 于点Q,且∠Q=15°,求∠ACQ的度数.
23.(12 分)如图,在折纸活动中,小李制作了一张 的纸片,点 D, E 分别在边AB,AC 上,将 沿着 DE 折叠压平,A 与 重合.
(1)若 求 的度数;
(2)若 求 的度数.
24.(12分)已知一个角的两边与另一个角的两边分别平行,请结合图形回答下列问题:
(1)如图1,AB∥CD,BE∥DF,直接写出∠1与∠2的关系___________;
(2)如图 2,AB∥CD,BE∥DF,猜想∠1 与∠2 的关系,并说明理由;
(3)由(1)(2),我们可以得出结论:一个角的两边与另一个角的两边分别平行,那么这两个角_______________;
(4)应用:两个角的两边分别平行,且一个角比另一个角的 3 倍少60°,求这两个角的度数.
25.(14 分)【问题背景】∠MON=90°,点 A,B分别在OM,ON上运动(不与点O 重合).
图1 图2 图3
(1)【问题思考】如图1,AE,BE分别是∠BAO和∠ABO的平分线,随着点 A、点 B的运动,∠AEB=__________.
(2)如图2,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D=___________°.
②随着点A,B的运动,∠D的大小会变吗 如果不会,求∠D 的度数;如果会,请说明理由.
(3)【问题拓展】在图 2 的基础上,如果∠MON=α,其余条件不变,随着点A,B的运动(如图3),∠D=___________.(用含α的代数式表示)
参考答案
1. C 2. A 3. B 4. C 5. C 6. C 7. D 8. B 9. C 10. C
11. A 12. D
13.如果两个角相等,那么这两个角的余角相等
14.三角形的内角和是
15.160
17.15
19.解:(1)由①②得③;由①③得②;由②③得①.
(2)由①②,得③.
∥
又∵ ∥
20.解:(1)不能.
理由: ∥CD,即AE∥CF.
AE,CF都不是桌面或水平面,故不能说明桌面水平.
(2)能.理由:∵EF⊥CF,BD⊥CF,∴BD∥EF(在同一个平面内,垂直于同一条直线的两直线平行).∴能说明桌面是水平的.
21.解:(1)∠ADE=∠EFC,
理由:∵DE∥BC,∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,∴AB∥EF,∴∠B=∠EFC,
∴∠ADE=∠EFC.
(2)∵∠ACB=72°,∠A=60°,∴∠B=180°-∠A-∠ACB=48°,
∵CD⊥AB,∴∠BDC=90°,
∴∠DCB=180°-90°-48°=42°.
22.(1)证明:∵BC∥GE,∴∠E=∠1=50°,
∵∠AFG=∠1=50°,∴∠E=∠AFG=50°,∴AF∥DE.
(2)解:∵∠1=50°,∠Q=15°,∴∠AHD=∠1+∠Q=65°,
∵AF∥DE,∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°-∠CAQ-∠Q=100°.
23.解:(1)∵∠A+∠B+∠C=180°,
∴∠A=180°-(∠B+∠C)=180°-(50°+60°)=70°.
(2)∵△A'DE 是△ABC翻折变换而成,∴∠AED=∠A'ED,∠ADE=∠A'DE,∠A=∠A',
∴∠AED+∠ADE=∠A'ED+∠A'DE=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A,
24.(1)∠1=∠2
(2)解:∠1+∠2=180°.理由如下:
∵AB∥CD,∴∠1=∠3,
∵BE∥DF,∴∠2+∠3=180°,∴∠1+∠2=180°.
(3)相等或互补
(4)解:设一个角的度数为x,则另一个角的度数为3x-60°,
当x=3x-60°,解得 x=30°,则这两个角的度数分别为30°,30°;
当x+3x-60°=180°,解得x=60°,则这两个角的度数分别为 60°,120°.
综上所述,这两个角的度数分别为 30°,30°或60°,120°.
25.(1)135°
(2)①45
②解: 的度数不随点 A,B的移动而发生变化,设
∵AD平分
∵BC 平分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
