人教版六年级下册数学奥数专讲:正反比例的应用(课件)(共16张PPT)
文档属性
| 名称 | 人教版六年级下册数学奥数专讲:正反比例的应用(课件)(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 16:10:11 | ||
图片预览




文档简介
(共16张PPT)
第6讲:正反比例的应用
奥数六年级下册春季课程
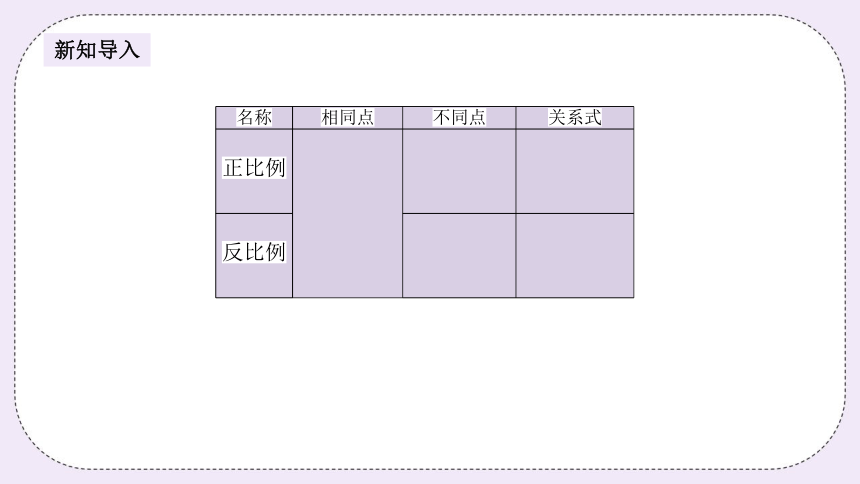
名称 相同点 不同点 关系式
正比例
反比例
新知导入
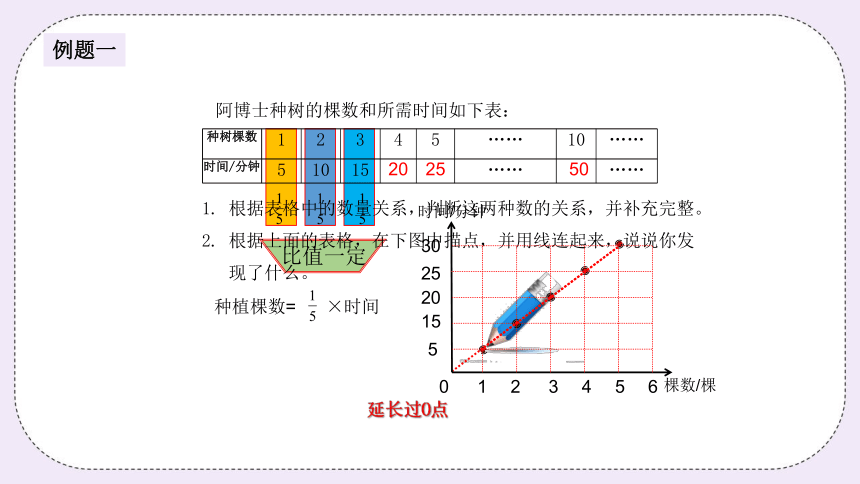
种树棵数 1 2 3 4 5 …… 10 ……
时间/分钟 5 10 15 …… ……
阿博士种树的棵数和所需时间如下表:
种植棵数= ×时间
比值一定
20
25
50
1. 根据表格中的数量关系,判断这两种数的关系,并补充完整。
2. 根据上面的表格,在下图中描点,并用线连起来,说说你发
现了什么。
延长过0点
5
4
3
2
1
6
0
20
5
15
25
30
时间/分钟
棵数/棵
例题一
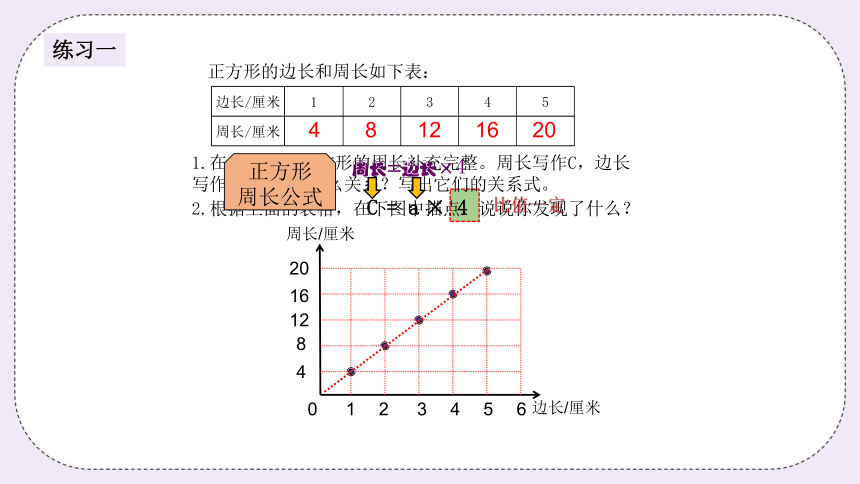
正方形的边长和周长如下表:
边长/厘米 1 2 3 4 5
周长/厘米
1.在上表中将正方形的周长补充完整。周长写作C,边长写作a,它们是什么关系?写出它们的关系式。
2.根据上面的表格,在下图中描点,说说你发现了什么?
周长=边长×4
正方形
周长公式
C
= a
× 4
比值一定
4
12
8
20
16
5
4
3
2
1
6
0
12
4
8
16
20
周长/厘米
边长/厘米
练习一
米德骑着一辆自行车从家去学校,4分钟骑了240米,用同样的速度,再骑11分钟就能到达学校。米德家离学校有多远?(用比例的方法解题)
240÷4×(11+4)=900(米)
比例的基本性质:比例的内项之积等于外项之积
路程=速度×时间
速度一定,路程和时间成正比例关系
解:
设米德家离学校有 米远,
答:米德家离学校为900米。
例题二
阿博士家每只母鸭每天都生一个蛋,那么8只母鸭一周可以生几个蛋?(用比例的方法解题)
生产速度一定,每只鸭生产数量和时间成正比
统一单位
解:
设8只母鸭一周可以生 个蛋,
答:8只母鸭一周可以生产56个蛋。
练习二
1. 两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,那么这两个变量之间的关系就叫做正比例关系。一个量随着另一个量的增加而减少或一个量随着另一个量的减少而增加,且它们的乘积相同,那么这两个量就成反比例。
2. 比例的基本性质:两个外项的积等于两个内项的积。
小 结
长方形的长和周长成什么比例关系?
长
宽
宽一定呢?
成正比?
比值不一定
周长与长和宽的和成正比
长/厘米 5 6 7 8 9
周长/厘米 18 20 22 24 26
宽=4厘米
长方形的面积一定,长和宽成什么关系?
芭啦啦综合教育学校六年级(3)班有24个人排队做操,有以下几种排队方式:
列数 1 2 3
行数 6
1. 请将上表补充完整,并判断这两种数的关系。
2. 根据上表,在下图中描点,并用线连起来,说说你的发现。
总人数=行数×列数
总人数一定
乘积一定
反比例关系
24
12
8
4
4
3
2
1
0
12
4
8
16
20
行数
列数
24
不是一条直线
不经过0点
例题三
欧拉有60元学习进步奖,他想正好用完这笔钱,买几本相同的书送给小伙伴们,他有以下几种选择:
1.将上表补充完整,判断这两个数据的关系。
单价/元 5 10 12 15 20
本数
总金额=单价×数量
总金额一定
乘积一定
反比例关系
4
3
12
5
6
2.若用表示单价,用表示相对应的本数,列出其关系式,说说你的发现。
60
练习三
卡尔看一本书,若每天看25页,则8天刚好可以看完。卡尔打算5天正好看完,则每天需要看多少页?(用比例的方法解题)
工作总量=工作效率×时间
“一本书”一定
工作效率与时间成反比
解:
设每天需要看 页,
答:则每天需要看40页。
例题四
有一批货,共重48吨。大卡车每次可以运8吨,若干次后刚好可以运完;小卡车每次可以运4吨,若干次后也刚好运完。已知大、小卡车的速度相同,每运一次需要花2小时。则用大卡车比小卡车可节约多少时间?(用比例的方法解题)
大卡车运48÷8=6(次)
总重量一定,需要运的次数和每次运的总量成反比
解:
设小卡车运 次,
答:则用大卡车比小卡车节约12小时。
(12-6)×2=12(小时)
练习四
甲、乙、丙三人进行万米跑比赛,当甲到终点时,乙还有1千米,丙还有2千米,如果三个人都是匀速跑步,甲跑完全程要54分钟,乙、丙跑完全程分别要多少分钟?(用比例的方法解题)
甲
乙
丙
万米=10000米
相同的时间里,
甲跑了10000米,乙跑了9000米,丙跑了8000米
甲、乙、丙的速度比是10000:9000:8000
甲、乙、丙一起跑10000米,路程一定
时间和速度成反比
解:
设乙跑完全程要运 分钟,
路程和速度成正比
设丙跑完全程要运 分钟,
答:乙跑完全长需要60分钟,丙需要67.5分钟。
例题五
甲、乙两支不同的蜡烛,甲可以点4.5小时,乙可以点5小时,同时点燃3小时后,剩下的两支蜡烛的长度正好相等。问甲、乙蜡烛的长度比是多少?(用比例的方法解题)
看作“行程”问题
蜡烛的长度当作路程
燃烧速度当作速度
甲
乙
甲要“行驶”4.5-3=1.5(小时)
乙要“行驶”5-3=2(小时)
相同的“路程”里,速度和时间成反比
甲、乙的速度比是 2:1.5
总长度燃烧时间比是 4.5:5
路程=速度×时间
速度扩大到a倍,时间扩大到b倍,那么行驶的路程扩大到几倍呢?
扩大到a×b倍
速度先扩大到a倍,时间不变,路程成正比,路程扩大到a倍。再扩大后的“速度”不变,时间扩大到b倍,那么行驶的“路程”再扩大到b倍。
设甲蜡烛的长度为C甲,乙蜡烛长度为C乙,
解:
燃烧速度:甲为C甲÷4.5,乙为C乙÷5,
(C甲÷4.5):(C乙÷5)=(5-3):(4.5-3)
C甲:C乙=6:5
答:甲、乙的长度比是6比5。
联想
甲、乙的长度比
=(2×4.5):(1.5×5)=6:5
练习五
1. 熟悉掌握正反比例关系的判断方法,并了解它的特点。
2. 会用正反比例关系的应用方法解题。
3. 速度扩大到a倍,时间扩大到b倍,行驶的路程扩大到ab倍。
小 结
课 程 结 束
奥数六年级下册春季课程
第6讲:正反比例的应用
奥数六年级下册春季课程
名称 相同点 不同点 关系式
正比例
反比例
新知导入
种树棵数 1 2 3 4 5 …… 10 ……
时间/分钟 5 10 15 …… ……
阿博士种树的棵数和所需时间如下表:
种植棵数= ×时间
比值一定
20
25
50
1. 根据表格中的数量关系,判断这两种数的关系,并补充完整。
2. 根据上面的表格,在下图中描点,并用线连起来,说说你发
现了什么。
延长过0点
5
4
3
2
1
6
0
20
5
15
25
30
时间/分钟
棵数/棵
例题一
正方形的边长和周长如下表:
边长/厘米 1 2 3 4 5
周长/厘米
1.在上表中将正方形的周长补充完整。周长写作C,边长写作a,它们是什么关系?写出它们的关系式。
2.根据上面的表格,在下图中描点,说说你发现了什么?
周长=边长×4
正方形
周长公式
C
= a
× 4
比值一定
4
12
8
20
16
5
4
3
2
1
6
0
12
4
8
16
20
周长/厘米
边长/厘米
练习一
米德骑着一辆自行车从家去学校,4分钟骑了240米,用同样的速度,再骑11分钟就能到达学校。米德家离学校有多远?(用比例的方法解题)
240÷4×(11+4)=900(米)
比例的基本性质:比例的内项之积等于外项之积
路程=速度×时间
速度一定,路程和时间成正比例关系
解:
设米德家离学校有 米远,
答:米德家离学校为900米。
例题二
阿博士家每只母鸭每天都生一个蛋,那么8只母鸭一周可以生几个蛋?(用比例的方法解题)
生产速度一定,每只鸭生产数量和时间成正比
统一单位
解:
设8只母鸭一周可以生 个蛋,
答:8只母鸭一周可以生产56个蛋。
练习二
1. 两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,那么这两个变量之间的关系就叫做正比例关系。一个量随着另一个量的增加而减少或一个量随着另一个量的减少而增加,且它们的乘积相同,那么这两个量就成反比例。
2. 比例的基本性质:两个外项的积等于两个内项的积。
小 结
长方形的长和周长成什么比例关系?
长
宽
宽一定呢?
成正比?
比值不一定
周长与长和宽的和成正比
长/厘米 5 6 7 8 9
周长/厘米 18 20 22 24 26
宽=4厘米
长方形的面积一定,长和宽成什么关系?
芭啦啦综合教育学校六年级(3)班有24个人排队做操,有以下几种排队方式:
列数 1 2 3
行数 6
1. 请将上表补充完整,并判断这两种数的关系。
2. 根据上表,在下图中描点,并用线连起来,说说你的发现。
总人数=行数×列数
总人数一定
乘积一定
反比例关系
24
12
8
4
4
3
2
1
0
12
4
8
16
20
行数
列数
24
不是一条直线
不经过0点
例题三
欧拉有60元学习进步奖,他想正好用完这笔钱,买几本相同的书送给小伙伴们,他有以下几种选择:
1.将上表补充完整,判断这两个数据的关系。
单价/元 5 10 12 15 20
本数
总金额=单价×数量
总金额一定
乘积一定
反比例关系
4
3
12
5
6
2.若用表示单价,用表示相对应的本数,列出其关系式,说说你的发现。
60
练习三
卡尔看一本书,若每天看25页,则8天刚好可以看完。卡尔打算5天正好看完,则每天需要看多少页?(用比例的方法解题)
工作总量=工作效率×时间
“一本书”一定
工作效率与时间成反比
解:
设每天需要看 页,
答:则每天需要看40页。
例题四
有一批货,共重48吨。大卡车每次可以运8吨,若干次后刚好可以运完;小卡车每次可以运4吨,若干次后也刚好运完。已知大、小卡车的速度相同,每运一次需要花2小时。则用大卡车比小卡车可节约多少时间?(用比例的方法解题)
大卡车运48÷8=6(次)
总重量一定,需要运的次数和每次运的总量成反比
解:
设小卡车运 次,
答:则用大卡车比小卡车节约12小时。
(12-6)×2=12(小时)
练习四
甲、乙、丙三人进行万米跑比赛,当甲到终点时,乙还有1千米,丙还有2千米,如果三个人都是匀速跑步,甲跑完全程要54分钟,乙、丙跑完全程分别要多少分钟?(用比例的方法解题)
甲
乙
丙
万米=10000米
相同的时间里,
甲跑了10000米,乙跑了9000米,丙跑了8000米
甲、乙、丙的速度比是10000:9000:8000
甲、乙、丙一起跑10000米,路程一定
时间和速度成反比
解:
设乙跑完全程要运 分钟,
路程和速度成正比
设丙跑完全程要运 分钟,
答:乙跑完全长需要60分钟,丙需要67.5分钟。
例题五
甲、乙两支不同的蜡烛,甲可以点4.5小时,乙可以点5小时,同时点燃3小时后,剩下的两支蜡烛的长度正好相等。问甲、乙蜡烛的长度比是多少?(用比例的方法解题)
看作“行程”问题
蜡烛的长度当作路程
燃烧速度当作速度
甲
乙
甲要“行驶”4.5-3=1.5(小时)
乙要“行驶”5-3=2(小时)
相同的“路程”里,速度和时间成反比
甲、乙的速度比是 2:1.5
总长度燃烧时间比是 4.5:5
路程=速度×时间
速度扩大到a倍,时间扩大到b倍,那么行驶的路程扩大到几倍呢?
扩大到a×b倍
速度先扩大到a倍,时间不变,路程成正比,路程扩大到a倍。再扩大后的“速度”不变,时间扩大到b倍,那么行驶的“路程”再扩大到b倍。
设甲蜡烛的长度为C甲,乙蜡烛长度为C乙,
解:
燃烧速度:甲为C甲÷4.5,乙为C乙÷5,
(C甲÷4.5):(C乙÷5)=(5-3):(4.5-3)
C甲:C乙=6:5
答:甲、乙的长度比是6比5。
联想
甲、乙的长度比
=(2×4.5):(1.5×5)=6:5
练习五
1. 熟悉掌握正反比例关系的判断方法,并了解它的特点。
2. 会用正反比例关系的应用方法解题。
3. 速度扩大到a倍,时间扩大到b倍,行驶的路程扩大到ab倍。
小 结
课 程 结 束
奥数六年级下册春季课程
