江苏省泰州市泰兴市2023-2024学年八年级上学期期末数学试题(含答案)
文档属性
| 名称 | 江苏省泰州市泰兴市2023-2024学年八年级上学期期末数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-03 21:29:25 | ||
图片预览


文档简介
2023年秋学期八年级期末学情调查数学试题
(考试时间:120分钟 满分:150分)
请注意:
1.本试卷分选择题和非选择题两个部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分选择题(共18分)
一、选择题(本大题共有6小题,每小题3分,共18分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.泰兴市创建文明城市,全市人民自觉遵守交通规则,文明出行,共建和谐下列交通标志是轴对称图形的是( )
A.B.C.D.
2.在实数(每两个1之间依次增加1个2)中,无理数有( )个.
A.1个 B.2个 C.3个 D.4个
3.下列函数中,函数值随自变量增大而增大的是( ).
A. B. C. D.
4.近似数6.16万精确到( ).
A.百分位 B.千分位 C.百位 D.万位
5.如图,已知小红的坐标为,小亮的坐标为,那么小华的坐标为( ).
A. B. C. D.
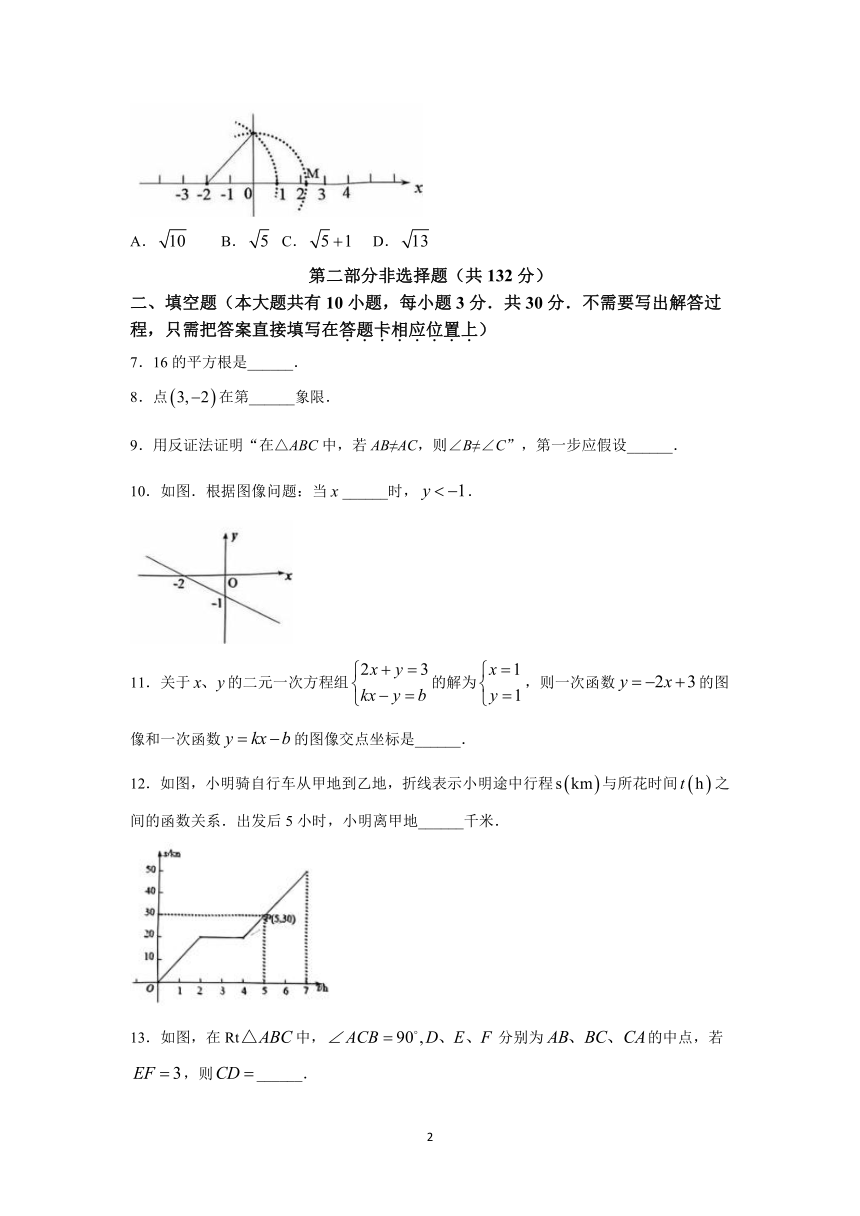
6.如图,根据尺规作图痕迹,判断点在数轴上表示的数是( ).
A. B. C. D.
第二部分非选择题(共132分)
二、填空题(本大题共有10小题,每小题3分.共30分.不需要写出解答过程,只需把答案直接填写在答题卡相应位置上)
7.16的平方根是______.
8.点在第______象限.
9.用反证法证明“在△ABC中,若AB≠AC,则∠B≠∠C”,第一步应假设______.
10.如图.根据图像问题:当______时,.
11.关于的二元一次方程组的解为,则一次函数的图像和一次函数的图像交点坐标是______.
12.如图,小明骑自行车从甲地到乙地,折线表示小明途中行程与所花时间之间的函数关系.出发后5小时,小明离甲地______千米.
13.如图,在Rt中,分别为的中点,若,则______.
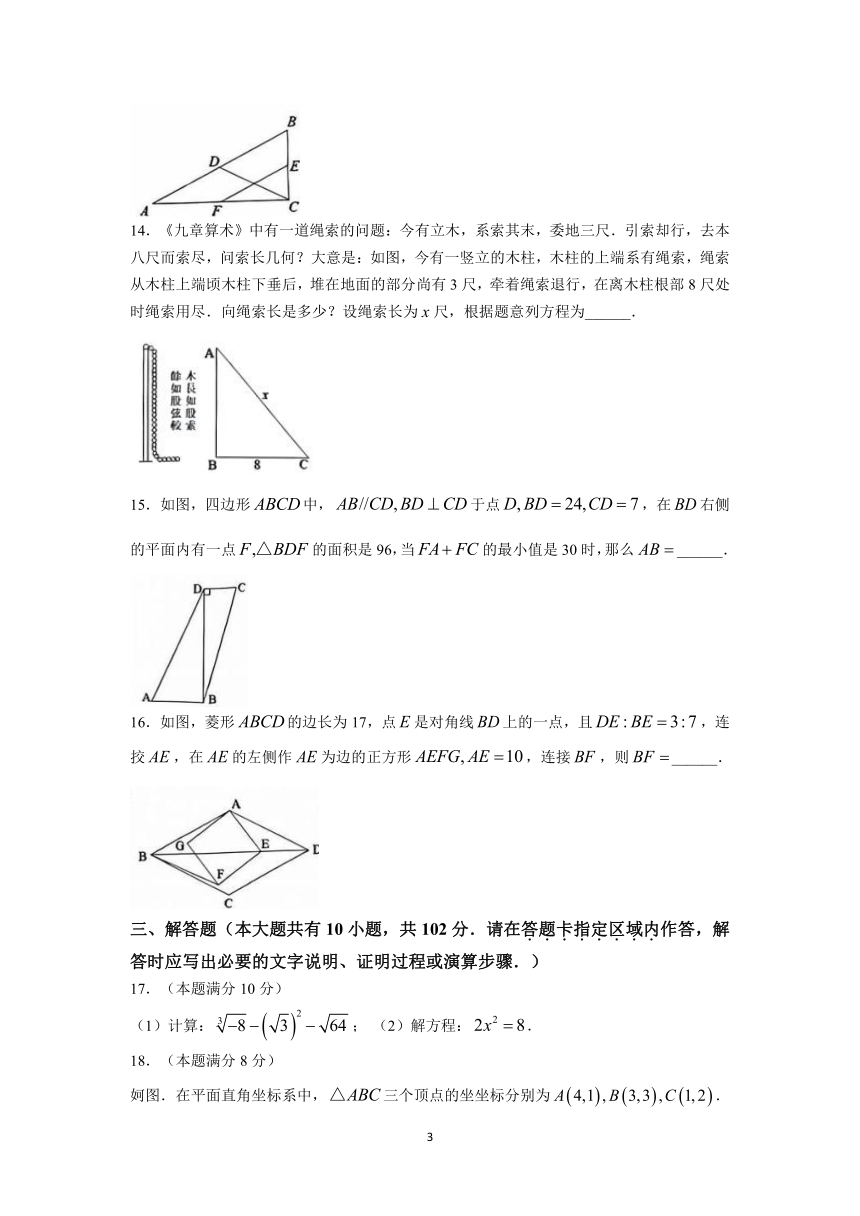
14.《九章算术》中有一道绳索的问题:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?大意是:如图,今有一竖立的木柱,木柱的上端系有绳索,绳索从木柱上端顷木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽.向绳索长是多少?设绳索长为尺,根据题意列方程为______.
15.如图,四边形中,于点,在右侧的平面内有一点的面积是96,当的最小值是30时,那么______.
16.如图,菱形的边长为17,点是对角线上的一点,且,连挍,在的左侧作为边的正方形,连接,则______.
三、解答题(本大题共有10小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤.)
17.(本题满分10分)
(1)计算:; (2)解方程:.
18.(本题满分8分)
妸图.在平面直角坐标系中,三个顶点的坐坐标分别为.
(1)画出关于原点对称的,点的对应点分别是:
(2)两出绕点顺时针旅转后,得到的,点的对应点分别是点;
(3)的面积为______.
19.(本題满分8分)
2023年3月22日是第三十一届“世界水日”,联合国呼吁全世界关注和重视水资源的重要性.小明同学发现水龙头关闭不严会造成滴水浪费.为了倡议全校同学节约用水,他做了如下试验:用一个足够大的量杯,放置在水龙头下观察量杯中水量的变化情况.已知量杯中原来装有水,内7个时间点量杯中的水量变化如下表所示,其中表示时间,表示量杯中的水量.
时间 0 5 10 15 20 25 30
量杯中的水量 10 20 30 40 50 60 70
解决下列问题:
(1)在平面直角坐标系中,描出上表中以各对对应值为坐标的点并连线;
(2)结合表中数据写出墨杯中的水量关于时间的函数表达式______(不要求写自变量的取值范围);
(3)在这种漏水状态下,若不及时关闭水龙头,估算照这样漏一天量杯中的水量约为多少.
20.(本题满分10分)
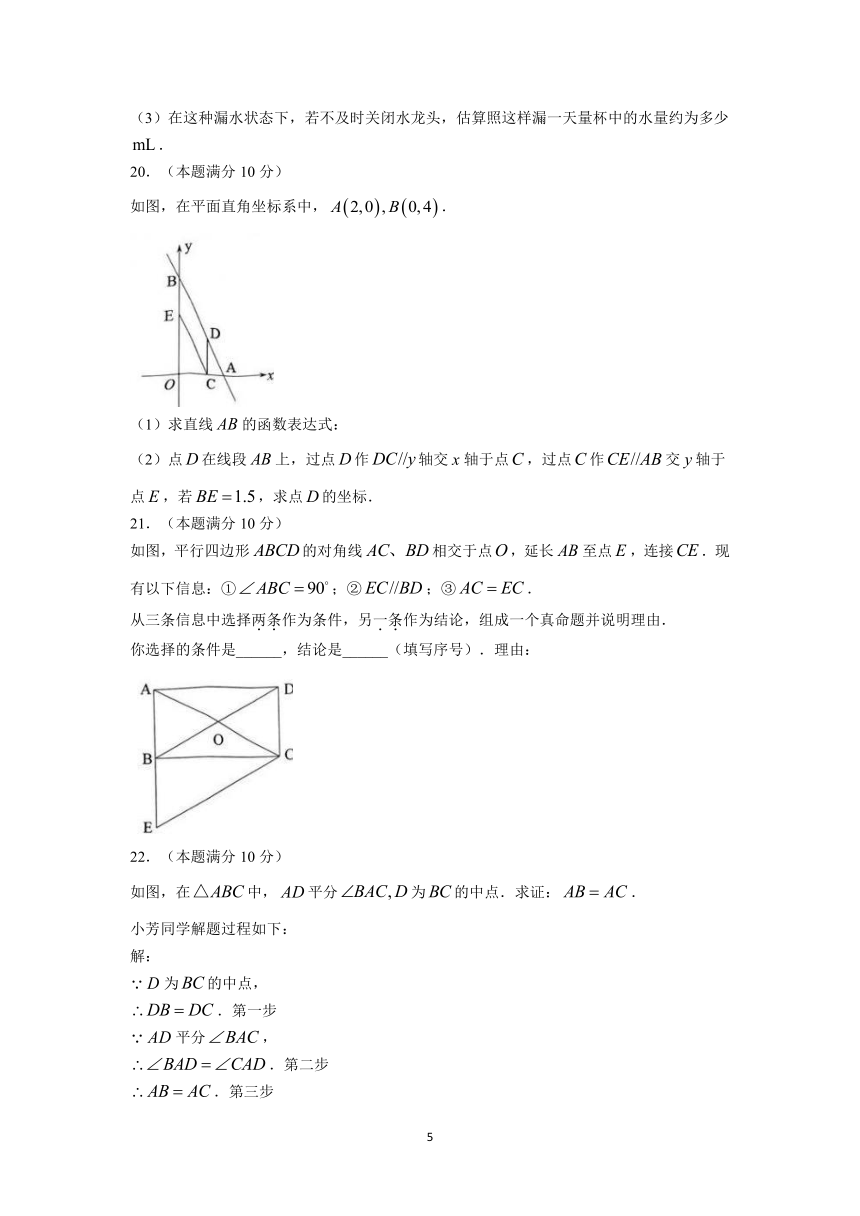
如图,在平面直角坐标系中,.
(1)求直线的函数表达式:
(2)点在线段上,过点作轴交轴于点,过点作交轴于点,若,求点的坐标.
21.(本题满分10分)
如图,平行四边形的对角线相交于点,延长至点,连接.现有以下信息:①;②;③.
从三条信息中选择两条作为条件,另一条作为结论,组成一个真命题并说明理由.
你选择的条件是______,结论是______(填写序号).理由:
22.(本题满分10分)
如图,在中,平分为的中点.求证:.
小芳同学解题过程如下:
解:
为的中点,
.第一步
平分,
.第二步
.第三步
(1)小芳同学解题过程中,出现错误的是第______步;
(2)写出正确的解题过程.
23.(本题满分10分)
如图,在正方形中,点是边上一点(不与点重合),过点作于点,交延长线于点.
(1)求证:.
(2)点从点向点运动过程中,设,,求与的函数表达式,并写出自变量的取值范围.
24.(本题满分10分)
(1)一次函数的图像上每个点的横坐标不变,纵坐标都增加1个单位长度后,得到的函数图像表达式是______.
(2)①一次函数的图像上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图像表达式是______.
A. B. C.
②一次函数的图像上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图像表达式是,求的值.
25.(本题满分12分)
八上数学课本69页,数学活动《折纸与证明》中告诉我们:折纸常常能为证明一个命题提供思路和方法,请用所学知识解决下列问题.
(1)如图1,一个三角形的纸片中,,证明:.
小龙同学通过折叠纸片,将折叠到上,点与点重合,展开后得到折痕,如图2,折痕交于点,连接.
帮助小龙同学写出证明过程.
(2)如图3,在平面直角坐标系中,点,点.直线交轴于点.
①求点坐标;
②直线过点,交轴于点,且,直线沿轴翻折恰好经过点,只用圆规在直线上求作点,使与直线所夹的锐角等于.(不写作法,保留作图痕迹)
③直接写出(2)中点的坐标.
26.(本题满分14分)
如图1,在四边形中,是等边三角形,点是直线上(异于点)的动点,点绕着点逆时针旋转至点处,连接.
(1)______°.
(2)当点在线段上时,如图2,连接.
①求证:;
②在线段上一定存在一个定点,满足,请说明理由.
(3)当点在直线上时,②中的结论还成立吗?说明理由.
2023年秋学期期末学情调查八年级数学答案
一.选择题
题号 1 2 3 4 5 6
答案 D B B C D B
二.填空题
7.. 8.四. 9.. 10.. 11.. 12.30.
13.3. 14.. 15.9 16..
三.解答题(共10小题)
17.(10分)
(1)解:原式
(2)解:
18.(8分)
(1)见图(2)见图(3)
19.(8分)
(1)见图
(2) (3)2890
20.(10分)
(1)
(2)轴,,为平行四边形
D在上点横坐标为
21.(10分)
(1)①②③或①③②或②③①
若选①②③
四边形为矩形
为平行四边形
若选①③②
.
四边形BDCE是平行四边形
若选②③①
四边形BDCE是平行四边形
四边形是矩形
22.(10分)
(1)三
(2)方法一:过作于于.
证得.
证得.
方法二:延长到,使,连接.
证得.
23.(10分)
(1)证,得
(2)
24.(10分)
(1)
(2)①B ② 2
25.(12分)(1)折叠
(2)
(3)以为圆心,以为半径作弧,交BM于
(4)
26.(14分)
(1)①
(2)①证
②法一:延长交于点.
.
等边.
在Rt中,
在Rt中,
法二:延长交于点.
.
等边.
在Rt中,
在Rt中,
(2)不一定成立.
当点在射线上时成立;(见图1、图2)
当点在延长线上时,或(见图3、图4)
(考试时间:120分钟 满分:150分)
请注意:
1.本试卷分选择题和非选择题两个部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分选择题(共18分)
一、选择题(本大题共有6小题,每小题3分,共18分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.泰兴市创建文明城市,全市人民自觉遵守交通规则,文明出行,共建和谐下列交通标志是轴对称图形的是( )
A.B.C.D.
2.在实数(每两个1之间依次增加1个2)中,无理数有( )个.
A.1个 B.2个 C.3个 D.4个
3.下列函数中,函数值随自变量增大而增大的是( ).
A. B. C. D.
4.近似数6.16万精确到( ).
A.百分位 B.千分位 C.百位 D.万位
5.如图,已知小红的坐标为,小亮的坐标为,那么小华的坐标为( ).
A. B. C. D.
6.如图,根据尺规作图痕迹,判断点在数轴上表示的数是( ).
A. B. C. D.
第二部分非选择题(共132分)
二、填空题(本大题共有10小题,每小题3分.共30分.不需要写出解答过程,只需把答案直接填写在答题卡相应位置上)
7.16的平方根是______.
8.点在第______象限.
9.用反证法证明“在△ABC中,若AB≠AC,则∠B≠∠C”,第一步应假设______.
10.如图.根据图像问题:当______时,.
11.关于的二元一次方程组的解为,则一次函数的图像和一次函数的图像交点坐标是______.
12.如图,小明骑自行车从甲地到乙地,折线表示小明途中行程与所花时间之间的函数关系.出发后5小时,小明离甲地______千米.
13.如图,在Rt中,分别为的中点,若,则______.
14.《九章算术》中有一道绳索的问题:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽,问索长几何?大意是:如图,今有一竖立的木柱,木柱的上端系有绳索,绳索从木柱上端顷木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽.向绳索长是多少?设绳索长为尺,根据题意列方程为______.
15.如图,四边形中,于点,在右侧的平面内有一点的面积是96,当的最小值是30时,那么______.
16.如图,菱形的边长为17,点是对角线上的一点,且,连挍,在的左侧作为边的正方形,连接,则______.
三、解答题(本大题共有10小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤.)
17.(本题满分10分)
(1)计算:; (2)解方程:.
18.(本题满分8分)
妸图.在平面直角坐标系中,三个顶点的坐坐标分别为.
(1)画出关于原点对称的,点的对应点分别是:
(2)两出绕点顺时针旅转后,得到的,点的对应点分别是点;
(3)的面积为______.
19.(本題满分8分)
2023年3月22日是第三十一届“世界水日”,联合国呼吁全世界关注和重视水资源的重要性.小明同学发现水龙头关闭不严会造成滴水浪费.为了倡议全校同学节约用水,他做了如下试验:用一个足够大的量杯,放置在水龙头下观察量杯中水量的变化情况.已知量杯中原来装有水,内7个时间点量杯中的水量变化如下表所示,其中表示时间,表示量杯中的水量.
时间 0 5 10 15 20 25 30
量杯中的水量 10 20 30 40 50 60 70
解决下列问题:
(1)在平面直角坐标系中,描出上表中以各对对应值为坐标的点并连线;
(2)结合表中数据写出墨杯中的水量关于时间的函数表达式______(不要求写自变量的取值范围);
(3)在这种漏水状态下,若不及时关闭水龙头,估算照这样漏一天量杯中的水量约为多少.
20.(本题满分10分)
如图,在平面直角坐标系中,.
(1)求直线的函数表达式:
(2)点在线段上,过点作轴交轴于点,过点作交轴于点,若,求点的坐标.
21.(本题满分10分)
如图,平行四边形的对角线相交于点,延长至点,连接.现有以下信息:①;②;③.
从三条信息中选择两条作为条件,另一条作为结论,组成一个真命题并说明理由.
你选择的条件是______,结论是______(填写序号).理由:
22.(本题满分10分)
如图,在中,平分为的中点.求证:.
小芳同学解题过程如下:
解:
为的中点,
.第一步
平分,
.第二步
.第三步
(1)小芳同学解题过程中,出现错误的是第______步;
(2)写出正确的解题过程.
23.(本题满分10分)
如图,在正方形中,点是边上一点(不与点重合),过点作于点,交延长线于点.
(1)求证:.
(2)点从点向点运动过程中,设,,求与的函数表达式,并写出自变量的取值范围.
24.(本题满分10分)
(1)一次函数的图像上每个点的横坐标不变,纵坐标都增加1个单位长度后,得到的函数图像表达式是______.
(2)①一次函数的图像上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图像表达式是______.
A. B. C.
②一次函数的图像上每个点的横坐标扩大2倍,纵坐标不变,得到的函数图像表达式是,求的值.
25.(本题满分12分)
八上数学课本69页,数学活动《折纸与证明》中告诉我们:折纸常常能为证明一个命题提供思路和方法,请用所学知识解决下列问题.
(1)如图1,一个三角形的纸片中,,证明:.
小龙同学通过折叠纸片,将折叠到上,点与点重合,展开后得到折痕,如图2,折痕交于点,连接.
帮助小龙同学写出证明过程.
(2)如图3,在平面直角坐标系中,点,点.直线交轴于点.
①求点坐标;
②直线过点,交轴于点,且,直线沿轴翻折恰好经过点,只用圆规在直线上求作点,使与直线所夹的锐角等于.(不写作法,保留作图痕迹)
③直接写出(2)中点的坐标.
26.(本题满分14分)
如图1,在四边形中,是等边三角形,点是直线上(异于点)的动点,点绕着点逆时针旋转至点处,连接.
(1)______°.
(2)当点在线段上时,如图2,连接.
①求证:;
②在线段上一定存在一个定点,满足,请说明理由.
(3)当点在直线上时,②中的结论还成立吗?说明理由.
2023年秋学期期末学情调查八年级数学答案
一.选择题
题号 1 2 3 4 5 6
答案 D B B C D B
二.填空题
7.. 8.四. 9.. 10.. 11.. 12.30.
13.3. 14.. 15.9 16..
三.解答题(共10小题)
17.(10分)
(1)解:原式
(2)解:
18.(8分)
(1)见图(2)见图(3)
19.(8分)
(1)见图
(2) (3)2890
20.(10分)
(1)
(2)轴,,为平行四边形
D在上点横坐标为
21.(10分)
(1)①②③或①③②或②③①
若选①②③
四边形为矩形
为平行四边形
若选①③②
.
四边形BDCE是平行四边形
若选②③①
四边形BDCE是平行四边形
四边形是矩形
22.(10分)
(1)三
(2)方法一:过作于于.
证得.
证得.
方法二:延长到,使,连接.
证得.
23.(10分)
(1)证,得
(2)
24.(10分)
(1)
(2)①B ② 2
25.(12分)(1)折叠
(2)
(3)以为圆心,以为半径作弧,交BM于
(4)
26.(14分)
(1)①
(2)①证
②法一:延长交于点.
.
等边.
在Rt中,
在Rt中,
法二:延长交于点.
.
等边.
在Rt中,
在Rt中,
(2)不一定成立.
当点在射线上时成立;(见图1、图2)
当点在延长线上时,或(见图3、图4)
同课章节目录
