2.5等比数列前n项和
图片预览








文档简介
课件27张PPT。2.5 等比数列前n项和(1)新课标人教版数学学科高一年级下学期多媒体教学课件教学要求:
(1)掌握等比数列前n项和公式,并能用公式解决简单的问题.
(2)理解等比数列前n项和公式的推导方法.
(3)能利用等比数列前n项和公式及其性质求一些特殊数列的和.
(4)等比数列的求和公式应达到灵活运用.
(5)理解等差数列与等比数列简单组合的数列的前n项和.
教学重点:
等比数列前n项和公式及错位相减的思想. 教学难点:
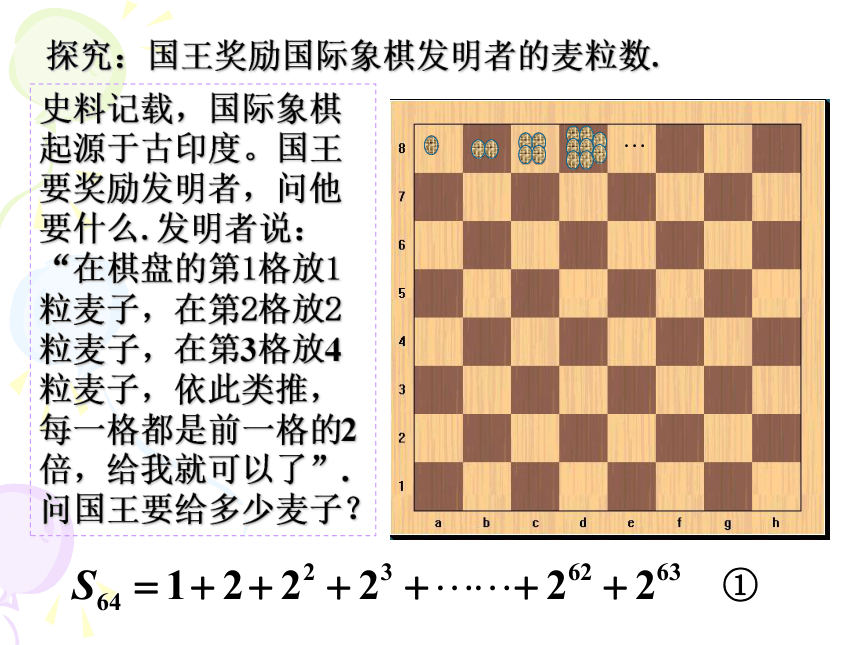
用错位相减法推导等比数列前n项和公式思路的获得.等比数列的概念:复习引新复习引新7.等比数列中“对称设”技巧:1. 等差数列前n项求和公式.2.用什么方法推导出了等差数列前n项求和公式?倒序相加法.复习引新探究:国王奖励国际象棋发明者的麦粒数.史料记载,国际象棋起源于古印度。国王要奖励发明者,问他要什么.发明者说:“在棋盘的第1格放1粒麦子,在第2格放2粒麦子,在第3格放4粒麦子,依此类推,每一格都是前一格的2倍,给我就可以了”.问国王要给多少麦子?①②②-①得探究:国王奖励国际象棋发明者的麦粒数. 这么多的麦粒,若铺在地球表面上,可以得出一个麦粒层,厚度约为9毫米.若以小麦千粒重为40g计算,则麦粒总质量达7000亿吨——国王是拿不出来的.我们关心的是这种求和的方法:它的特点是(1)乘公比,(2)错位相减(造成很多项相消去)求出和.
我们把这种求和方法称为:错位相减法.问题探究问题:能用以上方法求出等比数列前n项和吗?①②问题探究等比数列前n项求和公式:几个有用的公式例题解析例2.某商场今年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从今年起,大约几年内可使总销售量达到30000台(结果保留到个位).分析:应用题, 逆用求和公式 求n.例题解析基础训练在等差数列中在等比数列中例题解析基础训练C2.某超市去年的销售额为a万元,计划在后10年内每年比上一年增加10%,从今年起10年内这家超市的总销售额__________.基础训练小结等比数列前n项求和公式:说明:错位相减法求和.
方法步骤:(1)乘公比,(2)错位相减求出和.2.5 等比数列前n项和(2)新课标人教版数学学科高一年级下学期多媒体教学课件教学要求:
(1)掌握等比数列前n项和公式,并能用公式解决简单的问题.
(2)理解等比数列前n项和公式的推导方法.
(3)能利用等比数列前n项和公式及其性质求一些特殊数列的和.
(4)等比数列的求和公式应达到灵活运用.
(5)理解等差数列与等比数列简单组合的数列的前n项和.
教学重点:
等比数列前n项和公式及错位相减的思想. 教学难点:
用错位相减法推导等比数列前n项和公式思路的获得.复习回顾等比数列前n项求和公式:说明:错位相减法求和.
方法步骤:(1)乘公比,(2)错位相减求出和.例题解析问题二:如何向等差或等比数
列转化呢?每一项有什么特点?总结:
(1)判定数列是否为等差(比)数列;
(2)若不是,转化成等差(比)数列. (3)分组求和法.例题解析例题解析课堂练习课堂练习等比数列前n项求和公式:公式特点:错位相减法公式的应用小结
(1)掌握等比数列前n项和公式,并能用公式解决简单的问题.
(2)理解等比数列前n项和公式的推导方法.
(3)能利用等比数列前n项和公式及其性质求一些特殊数列的和.
(4)等比数列的求和公式应达到灵活运用.
(5)理解等差数列与等比数列简单组合的数列的前n项和.
教学重点:
等比数列前n项和公式及错位相减的思想. 教学难点:
用错位相减法推导等比数列前n项和公式思路的获得.等比数列的概念:复习引新复习引新7.等比数列中“对称设”技巧:1. 等差数列前n项求和公式.2.用什么方法推导出了等差数列前n项求和公式?倒序相加法.复习引新探究:国王奖励国际象棋发明者的麦粒数.史料记载,国际象棋起源于古印度。国王要奖励发明者,问他要什么.发明者说:“在棋盘的第1格放1粒麦子,在第2格放2粒麦子,在第3格放4粒麦子,依此类推,每一格都是前一格的2倍,给我就可以了”.问国王要给多少麦子?①②②-①得探究:国王奖励国际象棋发明者的麦粒数. 这么多的麦粒,若铺在地球表面上,可以得出一个麦粒层,厚度约为9毫米.若以小麦千粒重为40g计算,则麦粒总质量达7000亿吨——国王是拿不出来的.我们关心的是这种求和的方法:它的特点是(1)乘公比,(2)错位相减(造成很多项相消去)求出和.
我们把这种求和方法称为:错位相减法.问题探究问题:能用以上方法求出等比数列前n项和吗?①②问题探究等比数列前n项求和公式:几个有用的公式例题解析例2.某商场今年销售计算机5000台,如果平均每年的销售量比上一年增加10%,那么从今年起,大约几年内可使总销售量达到30000台(结果保留到个位).分析:应用题, 逆用求和公式 求n.例题解析基础训练在等差数列中在等比数列中例题解析基础训练C2.某超市去年的销售额为a万元,计划在后10年内每年比上一年增加10%,从今年起10年内这家超市的总销售额__________.基础训练小结等比数列前n项求和公式:说明:错位相减法求和.
方法步骤:(1)乘公比,(2)错位相减求出和.2.5 等比数列前n项和(2)新课标人教版数学学科高一年级下学期多媒体教学课件教学要求:
(1)掌握等比数列前n项和公式,并能用公式解决简单的问题.
(2)理解等比数列前n项和公式的推导方法.
(3)能利用等比数列前n项和公式及其性质求一些特殊数列的和.
(4)等比数列的求和公式应达到灵活运用.
(5)理解等差数列与等比数列简单组合的数列的前n项和.
教学重点:
等比数列前n项和公式及错位相减的思想. 教学难点:
用错位相减法推导等比数列前n项和公式思路的获得.复习回顾等比数列前n项求和公式:说明:错位相减法求和.
方法步骤:(1)乘公比,(2)错位相减求出和.例题解析问题二:如何向等差或等比数
列转化呢?每一项有什么特点?总结:
(1)判定数列是否为等差(比)数列;
(2)若不是,转化成等差(比)数列. (3)分组求和法.例题解析例题解析课堂练习课堂练习等比数列前n项求和公式:公式特点:错位相减法公式的应用小结
